人致人行桥侧向振动中时滞影响的研究
刘 隆, 谢伟平
(武汉理工大学 土木工程与建筑学院, 武汉 湖北 430070)
随着我国经济建设的发展,城市交通量逐渐增大,道路不断拓宽,为了保证交通顺畅和行人安全,在车辆和行人密集的城市区域和主干道大多设置人行天桥或地下通道取代传统的人行斑马线。因建造成本和日常维护费用相对较低,人行桥的应用更为广泛。此外,跨河两岸区域的人流连接,以及巨型空间建筑不同功能区的人流连接也采用人行天桥(或室内人行通道)的连接方式,例如跨英国泰晤士河的千禧桥和四川绵阳安昌河人行景观桥。随着现代人行桥向轻质、大跨、纤柔方向发展,行人活动引起的结构振动越来越显著,这种振动往往不足以引起结构的安全性问题,但是常常会给桥上的行人带来不舒适感甚至出现恐慌心理。对于人行桥来说,桥的振动响应幅度除了与桥的振动方向(主要是竖向和侧向)和振动频率有关外、还与人的活动状态、持续时间等有关[1,2]。由人们活动引起的动力荷载显著作用的频率区间通常大约在1.5~2.5 Hz之间[3]。我国仅在GJJ 69-95《城市人行天桥与人行地道技术规范》中通过规定人行桥的1阶竖向频率必须大于3 Hz这一条件来避免人行桥共振问题,而对于桥梁结构振动特性与行人舒适度之间的关系没有任何涉及[1]。因此仅仅通过限制人行桥竖向振动频率来保证行人舒适性显然是不完善的。
自从伦敦的千禧桥发生人致大幅度侧向振动后,人行桥侧向振动的问题受到了国际工程界的广泛关注。目前工程界普遍认为,由行人引起的人行桥的侧向振动是由人的蛇形运动和桥产生共振而出现的。行人上桥后,最先是同时产生侧向和竖向的振动,桥一旦起振,更多的行人就会和桥的振动同步,进一步增加了桥的振动,进而引起桥的剧烈的侧向振动。人行桥的这种侧向振动产生的机理不同于一般的共振问题,直到最近还有新的实验成果出现,所以具有其自身的复杂性,国内目前在进行的为数不多的特殊的或者结构新颖的人行桥设计时,通常委托高校或相关科研院所对此进行专门的立项研究。因此,由行人引起的人行桥侧向振动以及振动控制问题是我国工程界目前亟待解决的热点问题之一。
近些年来,不同国家的研究人员也分别从数学和实用的角度提出了分析桥梁侧振的相关模型,如最早的Bachmann[4]将人行荷载用傅里叶级数来表示,他的研究指出人行桥的侧向频率应该大于3.4 Hz。Ji[5]把人体近似地看作线性单自由度系统,但进一步的研究表明,这一单自由度人体系统依赖频率的变化,并不能总是通过同样的质量,刚度和阻尼参数来表示[6]。Strogats[7]使用了较为精细的数学模型来描述桥的侧向振动,但这样的模型工程实际应用上存在较大的困难。Nakamura[8]则以实测数据为基础改进了单自由度模型。由于行人与桥实际作用的复杂性,上述各种模型即使是非常精细的纯数学模型也难免要包含假设方程项。因此,Nakamura以实测数据为基础提炼出的单自由度模型更便于实际工程应用。但是Nakamura的方程中包含较多的参数,除了反应桥梁结构特性的质量,阻尼和刚度外还涉及人群的同步状况和桥上人群的饱和度,桥梁频率对人桥同步的作用等等。这些参数都必须通过大量的实验、计算和观察得到,甚至某些参数现在还无法明确给出,比如描述桥梁结构频率对同步影响大小的函数就是因为实测数据不足而无法确定。当梁以一种特殊的侧向模态振动时,Nakamura[8]认为人行引起桥的侧向振动可以用一个单自由度振动模型来描述:
(1)
其中,
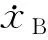
(2)
本文将从非线性动力学角度分析Nakamura模型中时间滞后对人群对桥梁结构动力作用的影响,并分析时滞是如何影响桥梁动力学行为的,进而提出通过改变桥面结构的方式减弱人致人行桥的振动的思路。
1 特征值分析
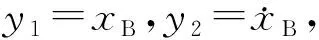
(3)
其中,

观察得知原点是方程(3)唯一的平衡点,将方程(3)在原点处线性化,其特征方程为
λ2+cBλ+kB-εk3λe-λτ=0
(4)
令τ=0,原方程(3)退化为常微分方程。此时特征方程变为
λ2+cBλ+kB-εk3λ=0
(5)
当cB-εk3=0时,(5)式有一对纯虚根
当cB-εk3>0时,(5)式的两根的实部都小于0,此时桥面的侧向振动能很快停下来。而当cB-εk3<0时,(5)式的两根的实部都大于0,桥的晃动会逐渐增大。令W=cB-εk3,将(5)式的两边对W求导,有
满足穿越条件。
根据Hopf分岔定理,在W=0附近系统将发生Hopf分岔,由于原点是系统唯一的平衡点,从而会产生出一个稳定的极限环。桥是否出现持续的侧向周期振动只与阻尼、人群的同步情况以及用于描述桥的结构频率对行人同步的影响函数G(fB)有关,而与桥的刚度无关。阻尼越大,桥产生侧向振动越困难。
下面考察方程(4)来研究时滞τ的影响。将λ=iω(ω>0)代入方程(4),分离实部和虚部,有
-ω2-ωsin(ωτ)εk3+kB=0
(6)
ω(cB-cos(ωτ)εk3)=0
(7)
将上两式两边同时平方消去时滞τ,得到
(8)
解得
其中,
设ω=ω1,2为方程(8)的两个正实根,根据方程组(6)和(7)有
(9)
则
其中,j=0,1,2,…。
根据根的分布理论,可能出现一对根来回穿越的情况,此时系统的稳定性也来回切换。时滞τ就有可能会影响到桥的侧向振动的发生。
2 时滞影响分析
为了分析时滞τ对桥侧向振动的影响,可利用中心流形定理和规范性理论[9]对桥侧向振动的稳态振幅受时滞τ的影响规律加以研究。可以求得j=0,在特征值穿越时,时滞特征值τ附近,动力系统(3)的定性行为如图1所示。
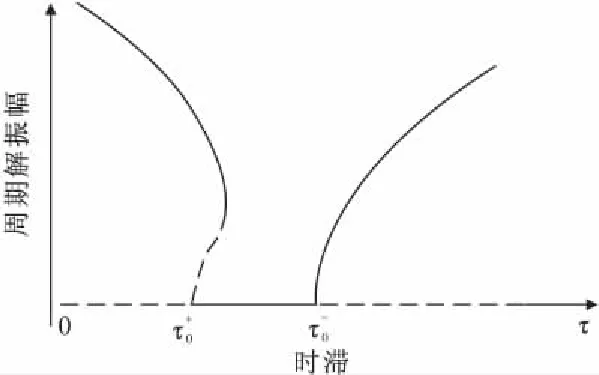
图1 j=0时τ的分岔示意
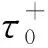
3 数值分析
使用文献[10]中桥梁参数做数值模拟,在(3)式中取MB=106132 kg,KB=179758 kg/s2,CB=8736 kg/s,k1=0.04,k2=0.2,k3=20,MPg=206550 N,则W=0.0823-0.3114G(fB)。当G(fB)=0.2643时,W=0。如果人对桥的反馈中不考虑时滞,则G(fB)>0.2643时桥发生侧向振动。分别取G(fB)=0.2和G(fB)=0.5。
G(fB)=0.2时,(8)式没有正实数解。因此τ的存在不影响系统的稳定性,不管时滞有多大,系统总是稳定。如图2,3所示,数值结果说明了分析的正确。
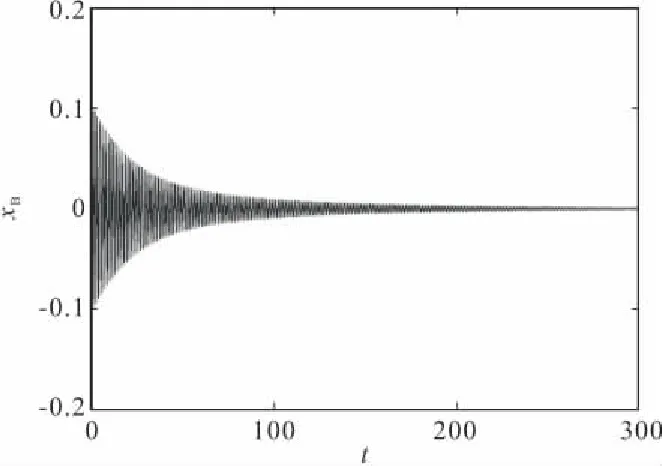
图2 G(fB)=0.2,τ=0,桥梁侧向振动时程
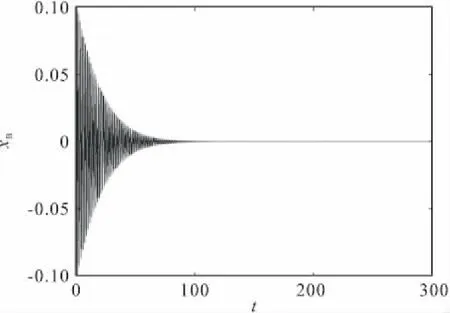
图3 G(fB)=0.2,τ=1,桥梁侧向振动时程
当G(fB)=0.5时,考虑(3)式中τ>0,则存在τ:0≤τ≤τ0,使得系统不稳定。当τ≥τ0时系统重新稳定下来。此时根据式(7),有
ω1=4.182, ω2=4.0499,
则:τ1j=0.2424+1.5j,τ2j=0.2503+1.55j,
其中,j=0,1,2,…。
根据根的穿越理论,此时有一对根从右半平面穿过虚轴,使得系统(3)的平衡点从不稳定到稳定。由于原点是系统(3)的唯一平衡点,因此时滞τ>0的存在使得产生周期解消失。上述分析过程如图4,5所示。
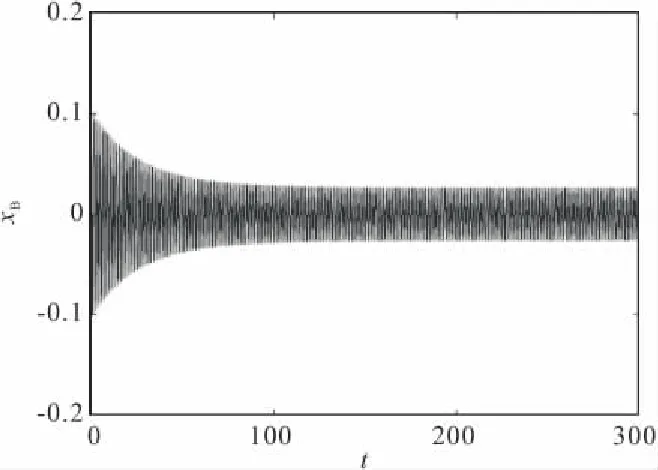
图4 G(fB)=0.5,τ=0,桥梁侧向振动时程

图5 G(fB)=0.5,τ=0.3,桥梁侧向振动时程
4 结 论
本文对Nakamura的单自由度桥梁侧向振动模型进行了全面的非线性分析。模型认为同步人群对桥侧向振动的作用相当于对于桥施加一个速度反馈。但实际上,人群对桥的作用不可能是瞬时产生的,而是存在一个时间滞后,本文考虑一个带时滞的作用力模型。当时间滞后不存在时,同步人群的比例越高,人群饱和度越大越容易导致人与桥的共振。桥梁的阻尼是唯一限制桥振动的因素。这些参量与桥侧向振动之间的关系可由式W=cB-εk3的符号来判断。当阻尼相对较大时桥的侧振容易停下来,甚至很难摆起。阻尼过小,或者同步人群增多或者人群饱和度加大,桥将被激起持续的侧向振动。研究发现时滞的出现可以使得桥的减振减小。当阻尼较大时,时滞使得桥更快趋向平衡位置;当阻尼较小,时滞可以使原来已经出现的侧向摆动停下来。
由此可以看出,时滞的作用对桥的侧向振动影响非常明显。一般来说,影响时滞的因素有两个,一个是内在的因素,人的反应时间,这是不可控的;另一个是外在的因素,人与桥面的接触材料的特性和厚度,接触材料越柔软、越厚则滞后越大,这是可以调节的。因此可以考虑通过设计桥面材料来控制桥梁侧向振动。详细的情况尚需进一步的理论和实验研究。
[1] Zivanovic S, Pavic A, Renolds P. Vibration serviceability of footbridge under human-induced excitation [J]. Journal of Sound and Vibration, 2005,279(1-2):1-74.
[2] Griffin M J. Handbook of Human Vibration[M]. London: Academic press,1996.
[3] Pachi A, Ji T. Frequency and velocity of people walking[J]. Structural Engineering, 2005, 83(3): 36-40.
[4] Bachmann H, Ammann W. Vibrations in Structures: Induced by Man and Machines (3ed) [M]. Zurich: International Association for Bridge and Structural Engineering (IABSE), 1987.
[5] Ji T. On the Combination of Structural Dynamics and Biodynamic Methods in the Study of Human-structure Interaction[C]//The 35th UK Group Meeting on Human Response to Vibration, Vol.1, Institute of Sound and Vibration Research. England: University of Sounthampton, 2000: 183-194.
[6] Sachse R. The Influence of Human Occupants on the Dynamic Properties of Slender Structures [D]. Sheffield: University of Sheffield, 2002.
[7] Strogats S H, Abrams D m, McRobie A, et al.Crowd synchrony on the Millennium Bridge [J]. Nature, 2005, 483(7064): 43-44.
[8] Nakamura S, Kawasaki T. A method for predicting the lateral girder response of footbridges induced by pedestrians [J]. Journal of Constructional Steel Research, 2009, 65(8-9):1705-1711.
[9] Hassard B D, Kazarinoff N D, Wang Y H. Theory and Application of Hopf Brifurcation [M]. Cambridge: Cambridge University Press, 1981.
[10] 赵国辉,刘健新. 人行天桥的侧向振动[C]// 第十七届全国桥梁学术会议(下册).重庆:重庆人民出版社,2006: 1111-1115.

