轻型TLP垂向振动的磁流变阻尼器半主动控制研究

，

(华南理工大学 土木与交通学院，广州 510641)

轻型张力腿平台(tension leg platform，TLP)是在传统型TLP的基础上提出来的，是一种适用于我国南海中浅水深海域石油开采的平台型式[1]。为了限制其平面内的运动(横荡、纵荡、艏摇)，需增大张力腿的刚度系数，进而影响其垂向振动响应，加之波浪的二阶力的影响，其垂向将产生高频振动springing及ringing，对结构强度及作业的顺利开展带来负面影响，必须对其进行垂向振动控制[2]。磁流变阻尼器广泛应用于土木工程的振动控制中，其具备控制力施加快速、出力大、能耗低、结构简单等优点，本文将其应用到TLP的垂向振动控制中，探讨其减振效果。

1 基于AQWA的水动力计算

1.1 AQWA分析流程

1)根据相关资料，在ANSYS传统界面中建立轻型TLP的三维模型，并使用壳单元shell63将模型表面划分成四边形网格。

2)使用“ANSTOAQWA”宏命令导出后缀名为aqwa的数据文件，更改后缀名为dat。

3)在dat文件中设置张力腿平台质量、波浪频率、波浪入射角等参数。在option cards卡片中添加CQTF、AQTF、NQTF选项，使用近场法求解，以用于输出后缀名为QTF的二进制文件，此文件包括了二阶波浪力的和频、差频矩阵，用于后续程序调用。

4)调用AQWA-LINE模块，输入dat文件进行求解。

5)使用AQWAGS进行后处理，输出张力腿平台6自由度RAO(response amplitude operator，幅值响应算子)，绘制频域下的一阶波浪力、附加质量、辐射阻尼等曲线图，并保存成后缀名为PTA的二进制文件，用于后续数值计算程序的调用。

1.2 AQWA中平台模型的建立

轻型张力腿平台的设计参数[3]见表1，工作水深120 m。二维模型、AQWA网格划分模型和计算模型见图1～3。

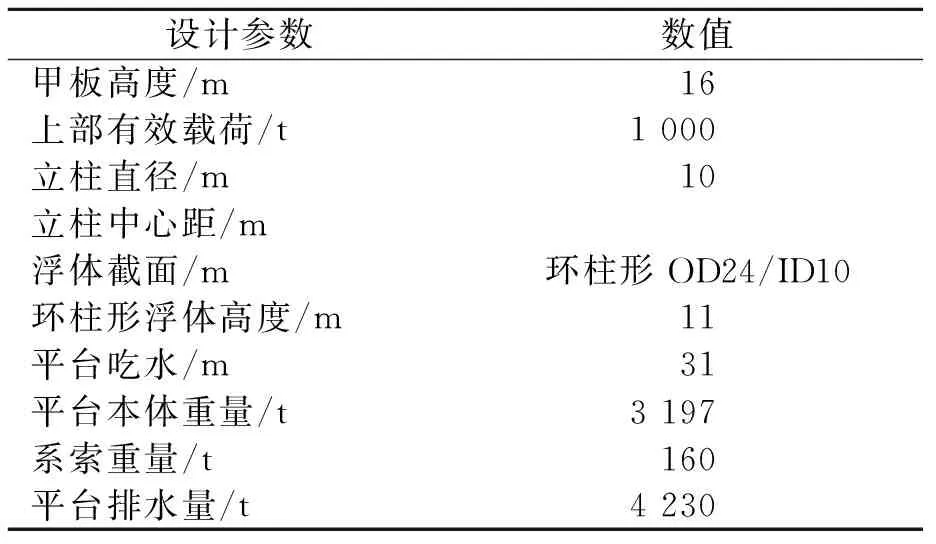
表1 轻型TLP主要设计参数

图1 轻型TLP的二维模型示意

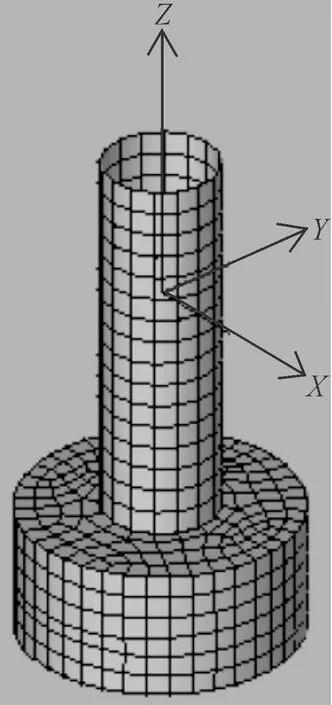
图2 轻型TLP的AQWA网格划分模型

图3 轻型TLP的AQWA计算模型

1.3 水动力参数

由AQWA计算得到TLP频域内单位波幅作用下的一阶波浪力、附加质量、辐射阻尼，见图4～6。

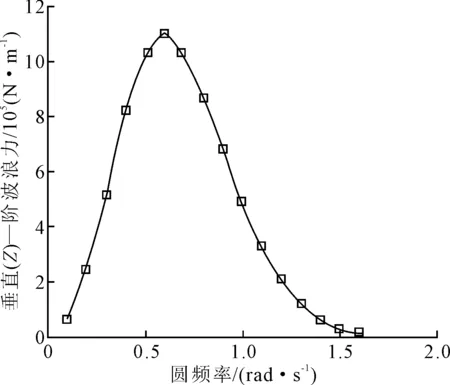
图4 单位波幅作用下垂向一阶波浪力

由图4可见，轻型TLP平台单位波幅作用下的垂向一阶波浪力的数量级可达106，受力较大，TLP将产生较大的垂向响应；由图5可知，当圆频率为0.5 rad·s-1时，TLP的附加质量取最大值，其数量级与平台自重较为接近；由图6可知，当圆频率为0.5 rad·s-1时，TLP的辐射阻尼取最大值，其数量级可达105，故在对轻型TLP进行振动分析时，附加质量以及辐射阻尼不可忽略。

图5 单位波幅作用下垂向(Z)附加质量

图6 单位波幅作用下垂向(Z)辐射阻尼

1.4 轻型TLP垂向振动周期

当张力腿平台的质量、作业水深一定时，张力腿的刚度系数是平台运动周期的主要影响因素。对于张力腿平台而言，当张力腿的刚度系数取值较小时，平台垂向运动频率较慢，但横摇、纵摇的运动位移较大，加大了石油开采的难度。当刚度系数取较大数值时，平台的垂向位移将减小，但是其垂向加速度则会变大，过大的垂向加速度同样会影响开采作业的进行，且会对平台的结构强度造成不利的影响；另外一方面，较大的刚度系数将有效地减小平台横荡及纵荡位移，有利于平台水平面内的定位，提高作业精度。本文研究的轻型TLP的工作水深为120 m，故其与在深水环境中作业的TLP的运动响应有所不同。

通过计算比较，选取张力腿刚度系数为K=1.2×108N/m;

平台的总重M=4.23×106kg;

可见，轻型TLP的垂向固有振动周期远低于深水工况下的一般周期(2～4 s)[4]，同时考虑到波浪二阶力可产生的高频振荡springing及ringing，平台的垂向运动响应会更剧烈，振荡更快，必须对其进行控制，以利于正常作业的进行。

2 轻型TLP垂向振动控制数值分析

使用MATLAB编写程序，由傅里叶变换，利用AQWA求出的频域下平台垂向的波浪力、附加质量及辐射阻尼等参数，求解时域下平台的迟滞函数以及广义波浪力脉冲响应函数后利用它们的卷积，单独求出时域下TLP所受波浪力的一阶和二阶分量；选取合适的积分方法，通过迟滞函数的积分求出时域下TLP的附加质量和辐射阻尼，最后选定数值计算方法并求解时域下的运动方程，从而得到其垂向运动响应。

2.1 无控状态下的垂向振动

选择JONSWAP谱进行波浪载荷的计算，谱密度定义如下。

(1)

式中：α——与风速和受风面积有关的常数，取0.008 1；

β——取1.25；

γ——谱峰升高因子，取3.3；

ωP——谱峰频率，取0.5。

对于无控状态下的张力腿平台，其垂向上的运动方程为

(ρgAw+k1)z0=F(t)

(2)

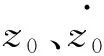
F(t)——TLP所受的波浪力，包括一阶与二阶波浪力；

m1——平台本体质量，m1=4.23×106kg；

c1——TLP的垂向阻尼，

c1=5.0×104N/(m·s)；

k1——张力腿刚度系数，k1=1.2×108N/m；

ma——附加质量，可利用傅里叶变换，通过迟滞函数的积分，由频域内的附加质量得到；

cr——附加阻尼，与速度有关，求解方法与附加质量相似；

Aw——TLP水线面面积，Aw=78.539 8 m2;

ρgAw——水线面刚度系数。

定义频率、阻尼比如下。

(3)

(4)

则式(2)可以改写成

(5)

二阶波浪力的近场解可以写成[5]

式中：Pij、Qij——与时间无关的同相和异相传递函数，也即AQWA算得的二阶波浪力的和频、差频矩阵，上标“+”表示实项，“-”表示虚项。

采用四阶龙格库塔法对上述运动方程求解，计算得到无控状态下TLP垂向所受波浪力及其振动位移、速度和加速度的时程曲线，见图7～10。

图7 无控状态下垂向波浪力

图8 无控状态下TLP垂向位移

由图7～10可见，无控状态下，轻型TLP所受的垂向波浪作用力的数值可达106数量级，由波浪作用力所引起的轻型TLP的垂向位移、速度、加速度同样不容小视，需对其进行垂向振动控制，以利于海上石油开采作业的顺利进行。

图9 无控状态下TLP垂向速度

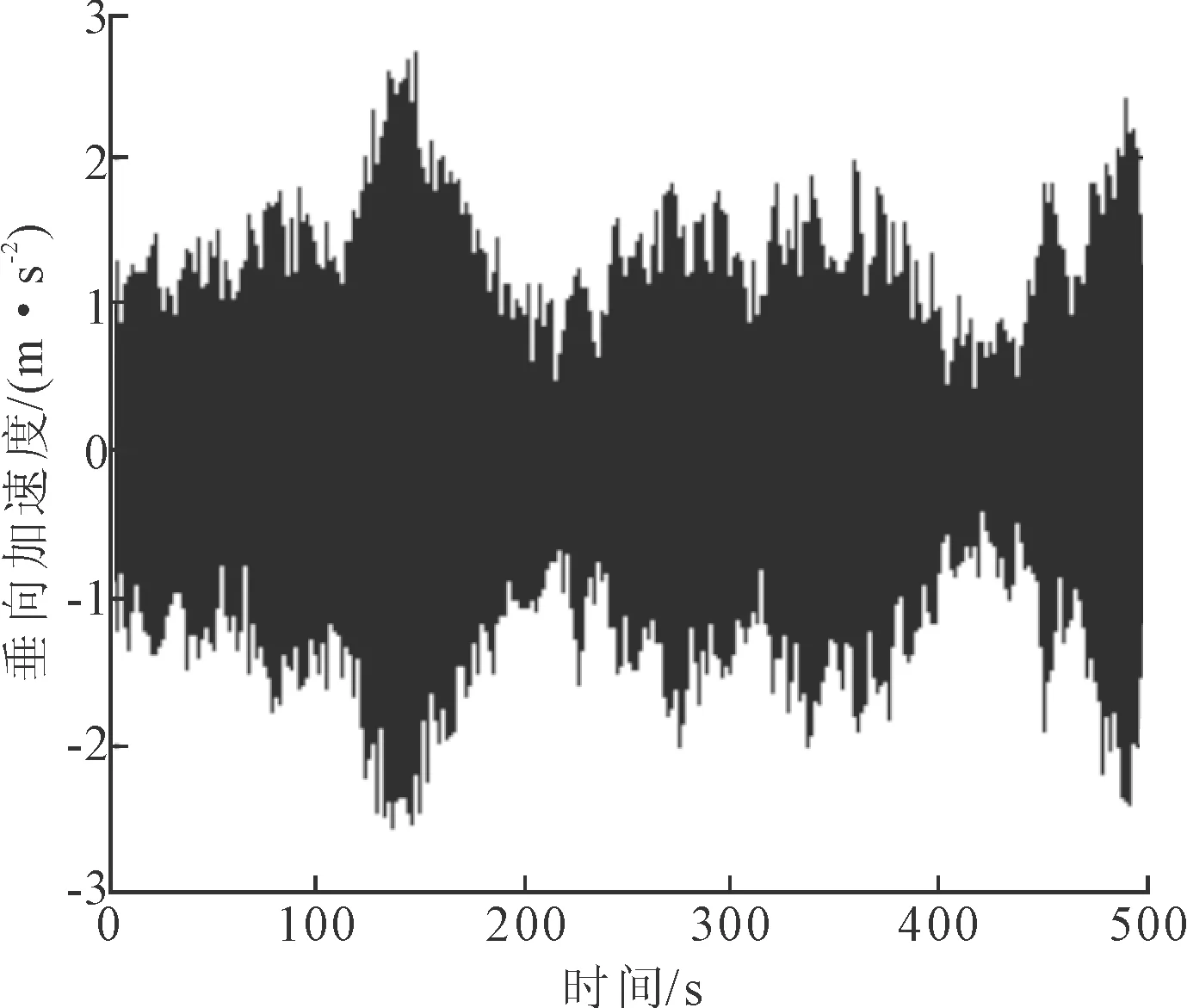
图10 无控状态下TLP垂向加速度

2.2 主动控制下的振动控制

采用LQR算法对TLP的垂向振动进行控制，为磁流变阻尼器的半主动控制提供控制力的参考。TLP在主动控制下的垂向运动方程为

(k1+ρgAw)z=F(t)+U(t)

(6)

式中：U(t)——主动控制力。

相应的状态方程为

(7)

Y(t)=C0Z(t)+D0F(t)+B0U(t)

(8)

A=

Y(t)——输出向量；

C0——输出向量；

B0、D0——控制力和波浪力的直接传递参数。

如何获取控制力U(t)是进行主动控制的关键问题，而确定出主动控制力的主动控制算法则是求解控制问题的重中之重。在对结构进行主动控制时，控制系统必须首先满足结构状态方程和各种约束条件，通过计算选取最佳的控制参数以及合适的增益矩阵，使控制性能指标最优，从而使得控制效果最好。

LQR算法采用时间变量的二次型性能指标，使得在任意时刻都能使目标函数的值最小。其采用的性能指标为[6]

(9)

式中：tf——外部激励的作用时间。

式(9)中Q和R分别是状态向量Z(t)及控制力向量U(t)的加权矩阵。Q越大，结构响应越小，控制力越大；R越小，控制力越大，结构响应越小。通过多次验算比较，本文在编制主动控制计算程序时，取

R=βI

式中:β=100，α=50；

I——结构维数对应，本文I为一维单位矩阵。

在闭环控制下，根据Riccati方程

-PA-ATP+PBR-1BTP-Q=0

(10)

可得控制力向量为

U(t)=-R-1BTPZ(t)

(11)

式(11)求得的U(t)即为最优主动控制力。从而由状态方程即可求解包括位移、速度、加速度在内的状态向量。

下面给出轻型TLP在主动控制下的垂向控制力、位移、速度、加速度时程图，见图11～14。

由图11可以看出，主动控制力较为合理。由图12～14可知，相较无控状态，TLP在主动控制作用下，其位移、速度和加速度值都有很明显的减小，即垂向振动控制效果显著。其中，最大位移值和最大速度值减小了约70%，加速度最大值减小了约60%。

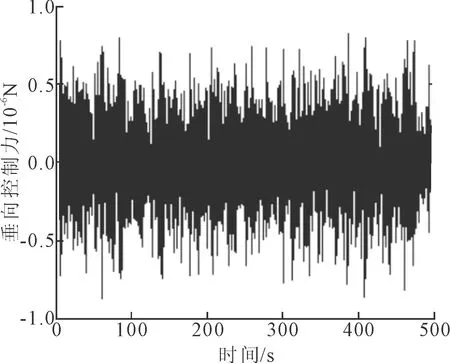
图11 主动控制作用力

图12 主动控制状态下TLP垂向位移

图13 主动控制状态下TLP垂向速度

图14 主动控制状态下TLP垂向加速度

2.3 磁流变阻尼器半主动控制

2.3.1 安装了磁流变阻尼器的结构振动控制方程

平台下体由8根张力腿与桩基相连，将磁流变阻尼器安装在张力腿与平台下体之间，阻尼器上端活塞杆与平台下体连接，下端活塞杆与张力腿连接，见图15。

图15 安装磁流变阻尼器的轻型TLP

对于本文研究的TLP，安装磁流变阻尼器后其相应的垂向运动方程可以表示为

(k1+ρgAw)z=F(t)+Us(t)

(12)

式中：Us(t)——磁流变阻尼器对TLP的半主动控制力。

磁流变阻尼器的阻尼力可以写为

(13)

cd，fdy——磁流变阻尼器的粘滞阻尼系数和可调库伦阻尼力。

式(13)中，第一项是被动粘滞阻尼力，不可调节控制；第二项为可调节控制的可变库伦阻尼力，可由半主动控制算法中的某一种，控制输入电流或电压的大小以调节磁场强度，使得磁流变液的屈服强度随之发生变化，从而获取控制算法预期的控制力。

2.3.2 半主动算法

通过LQR控制算法，确定出了施加在TLP垂向的最优主动控制力，磁流变阻尼器可提供的控制力需要尽可能地向最优主动控制力靠拢。磁流变阻尼器以阻尼力的形式提供与结构运动相反的力，因此磁流变阻尼控制具有很好的鲁棒性[7]。半主动磁流变阻尼控制算法主要包括简单的Bang-Bang控制算法、最优Bang-Bang控制算法及限界Hrovat最优控制算法三种，通过半主动控制算法，确定其实际可实现的阻尼力。

本文选取限界Hrovat控制算法来求解半主动控制力，可以表示为

式中:udmax——磁流变阻尼器相应于主动最优控制力u(t)时刻可能实现的最大阻尼力，

(14)

2.3.3 磁流变阻尼器半主动控制数值分析

参照主动控制算法所确定的主动控制力，设计TLP的磁流变阻尼器包括粘滞阻尼力在内的最大阻尼力等于相应的最大主动最优控制力，且假定其控制效果与主动控制一样。

假定磁流变阻尼器的最小库伦阻尼力fdymin=0，黏滞阻尼系数cd=0.875×104kN·s·m-1，最大库伦摩擦力fdymax=1.09×105kN。计算得到TLP在MR阻尼器半主动控制下的半主动控制力、位移、速度和加速度时程曲线见图16～19。

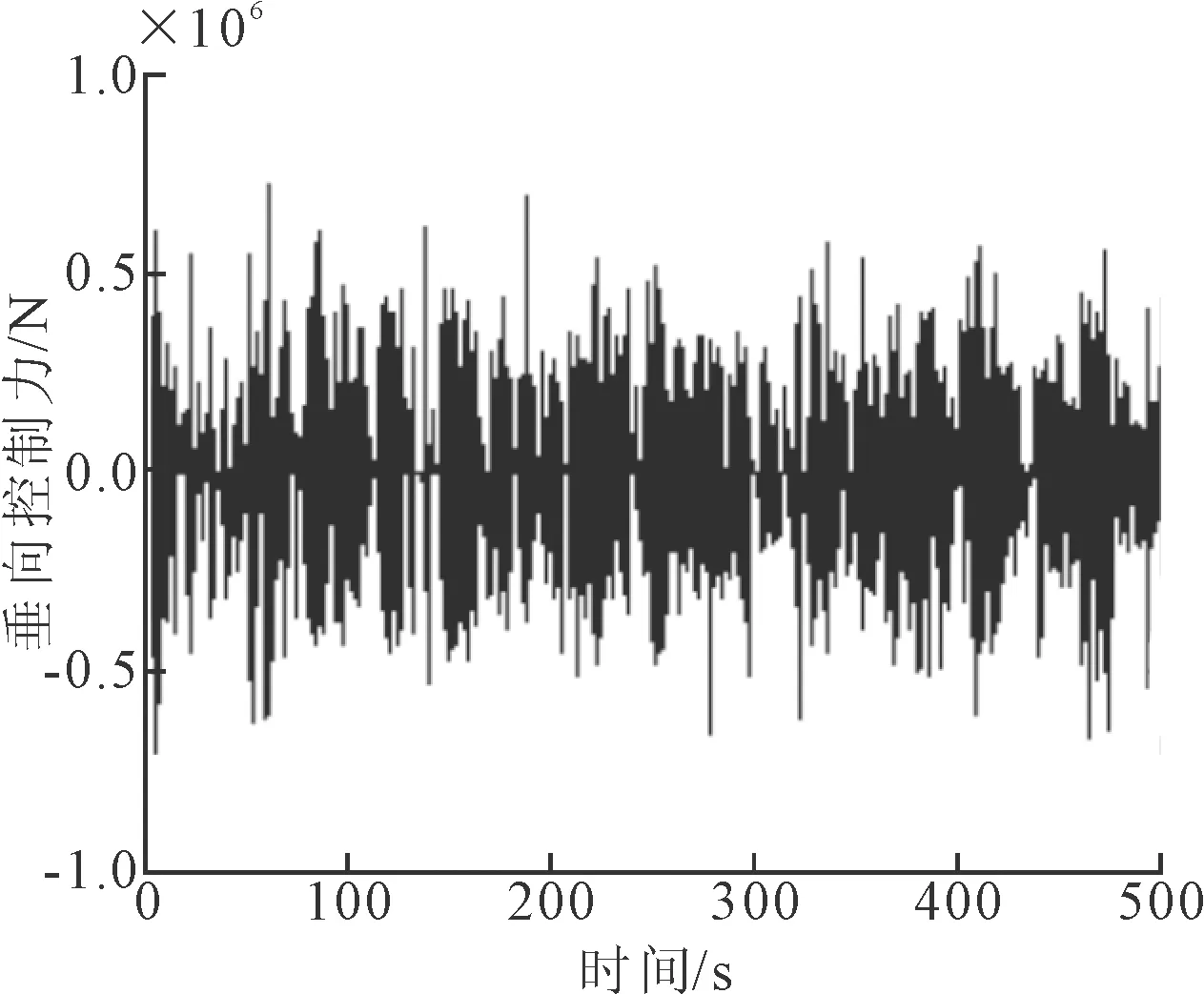
图16 磁流变阻尼器半主动控制作用力

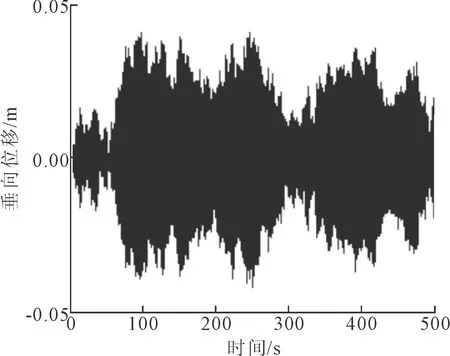
图17 半主动控制状态下TLP垂向位移

由图16～19可知，MR阻尼器对TLP的垂向振动也具有显著的减振效果。磁流变阻尼器可施加的半主动控制力与主动控制算法所确定的主动控制力较为接近，轻型TLP的垂向位移、速度、加速度值都有较大幅度地减小。

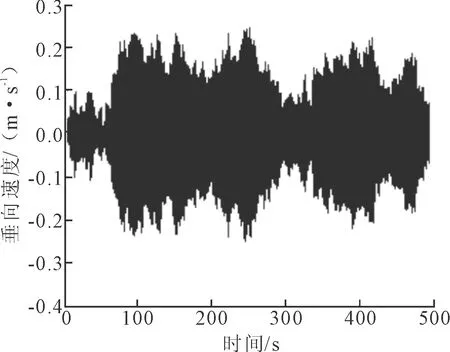
图18 半主动控制状态下TLP垂向速度

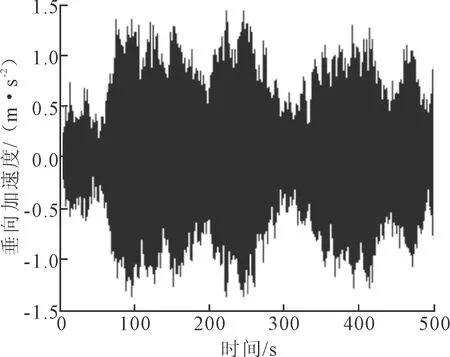
图19 半主动控制状态下TLP垂向加速度

2.4 三种状态下的控制效果对比

无控、主动控制及磁流变阻尼器半主动控制下TLP位移、速度及加速度的最大数值见表2。

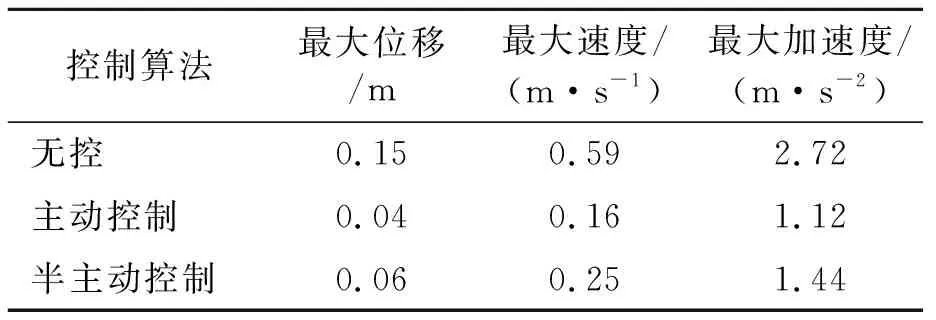
表2 三种情形下的垂向振动控制效果比较

由表2可见，磁流变阻尼器对轻型TLP的垂向振动具有明显的减振效果。其中，位移的最大减振值约为60%，速度的最大减振值约为57.6%，加速度的最大减振值约为47.1%。

3 结束语

磁流变阻尼器广泛应用于土木工程中，本文将其引入到轻型TLP的垂向振动控制中，数值分析表明其同样具有良好的减振效果。当前，海洋平台振动控制的研究主要集中于固定式导管架平台，且其被动控制、主动控制、半主动控制都有学者进行了理论研究和模型试验，但对移动式的TLP进行振动控制研究还比较少。相对于其它的平台型式，TLP具有特有的运动性能，对其进行振动控制研究，将提高石油开采的效率以及保障人员生命安全，延长平台使用年限，创造更大的经济效益。通过选取更加优良的主动控制算法和半主动控制律，并且考虑时滞影响，可对问题做更深入的研究。

[1] 鲍莹斌,苏 志,李润培.中等水深轻型张力腿平台型式研究[J].海洋工程,2001,19(2):7-12.

[2] 曾晓辉,沈晓鹏,徐本和,等.张力腿平台的水动力及结构力学问题[J].中国造船,2003,44(S):429-433.

[3] 肖宇维,孙树民.基于AQWA的轻型张力腿平台型式研究.科学技术与工程,2012,33(12)：8987-8993

[4] 张 智,董艳秋,唐友刚,等.1990年后世界TLP 平台的发展状况[J].中国海洋平台,2004,19(2):5-11.

[5] 祁 祺,张 涛,文 攀,等.基于AQWA的FPSO系泊系统响应数值模拟[J].舰船科学技术,2011,33(12): 14-18.

[6] 杜林平.磁流变阻尼器在柔性底层结构振动控制中的应用[D].广州:华南理工大学,2011.

[7] 欧进萍.结构振动控制-主动、半主动和智能控制[M].北京: 科学出版社,2003.