基于知识距离的不完备信息系统的决策规则提取

史 琨

(阳泉师范高等专科学校 计算机系，山西 阳泉 045200)

1982年，由Pawlak教授提出的粗糙集理论[1]，是处理不确定的、模糊的和不完备性问题的新型数学工具，并得到了广泛的应用[2～5].其主要思想是在保持分类能力不变的前提下，通过知识约简，导出问题的决策或分类规则.粗糙集作为一种有效的知识发现工具，已取得了令人瞩目的成果，同样有着很大的发展空间.

经典的粗糙集是以完备信息系统为研究对象，以等价关系为基础，通过等价关系对论域分成互不相交的等价类，划分越细，知识越丰富，信息越充分.然而，在实际问题中，有很多信息系统由于各种原因，信息达不到精确和确定，这就带来了一系列的问题，针对这类问题，基于不完备信息系统的决策规则提取得到了广泛的关注.本文通过基于知识距离提出的约简算法，针对不完备信息系统，提出了一种决策规则的提取方法，实例证明该方法求得的决策规则较好的解决了数据不精确和缺省的问题.

1 基本概念

如果对于至少一个属性a∈A，Va包含空值，则称S是一个不完备信息系统(Incomplete Information System)，否则它是完备的.这表明完备信息系统是不完备信息系统的一种特例.进一步，我们将用*表示空值.

设P⊆A，相容关系可以定义为:

SIM(P)={(u，v)∈U×U|∀a∈P，
a(u)=a(v)或a(u)=*或a(v)=*}；

易知

定义3[6]设S=(U，C∪D)是一个决策表，Xi∈U/C，Yj∈U/D，desC(Xi)是Xi在C下的唯一描述，desD(Yj)是Yj在D下的唯一描述.决策规则定义如下:

rij:desC(Xi)→desD(Yj)，Xi∩Yj≠Ø.

定义4[6]设有集合A和集合B，A和B的集合贴近度定义为:

其中0≤H(A，B)≤1.

定义5[6]设S=(U，A)是一个信息系统，P，Q⊆A，P和Q所对应的知识分别为:

U/SIM(P)={SP(x1)，SP(x2)，…，SP(x|U|)}

和

U/SIM(Q)={SQ(x1)，SQ(x2)，…，SQ(x|U|)}.

则知识U/SIM(P)和知识U/SIM(Q)的知识贴近度定义为:

定义6[6]设有集合A和集合B，A和B的集合差异度可以定义为:

定义7[6]设S=(U，A)是一个信息系统，P，Q⊆A，P和Q所对应的知识分别为:

U/SIM(P)={SP(x1)，SP(x2)，…，SP(x|U|)}

和

U/SIM(Q)={SQ(x1)，SQ(x2)，…，SQ(x|U|)}.

则知识U/SIM(P)和知识U/SIM(Q)的知识距离定义为:

定义8[6]设S=(U，A)是一个信息系统，a∈B⊆A是一个属性，则知识B中属性a的重要性定义为:

sigB(a)=D(B，B-{a}).

定义9[6]设S=(U，A)是一个信息系统，a∈B⊆A是一个属性，D(B，A)=0，sigB(a)=0，则知识B中属性a的不重要程度定义为:

unsigB(a)=D(B，{a}).

2 决策规则的获取

属性约简是粗糙集研究的核心内容之一，决策规则获取的问题归根结底就是属性约简的问题.然而，就不完备信息系统而言，决策规则获取的关键则是条件属性的约简.

一个决策算法的约简通常包含两部分，一部分是在整个算法中去掉所有可省略的条件属性，另一部分是对算法中的每一个规则进行约简.这两部分的顺序没有特别的要求，先进行哪部分都行，本文采取先对条件属性集约简的方法来获取决策规则.

由于借鉴了基于知识距离的信息系统属性约简算法[6]，其算法描述如下:

输入:信息系统S=(U，A)；

输出:S的一个约简C；

Step1:令B=core(A);

Step2:如果D(B，A)==0，使得C=B，结束算法;否则选择一个满足以下条件的属性a:

sigB∪{a}(a)=max{sigB∪{a'}(a')|a'∈A-B}，

令B=B∪{a}，转Step2.

针对不完备信息系统，利用上述算法，对条件属性集进行约简，得到的约简结果与决策属性构成了新的属性集，以新的属性集为条件，对信息系统求决策规则;再对所得的决策规则进行相应的合并，最后获得的约简结果即为相对最优的决策规则.

3 实例分析

例1 表1是一个描述小汽车信息的非完备信息系统.其中U={x1，x2，x3，x4，x5，x6}，C={c1，c2，c3，c4，c5}，这里c1，c2，c3，c4，c5表示Price，Mileage，Power，Size，Max-Speed，D={c6}，c6表示Quality.

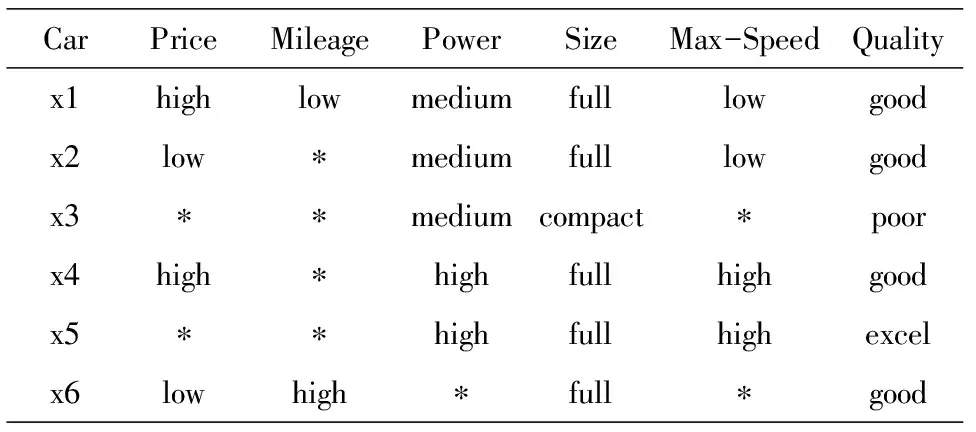
表1 一个关于小汽车的不完备信息系统

(1)根据算法对条件属性集C进行约简，由表1得:

U/SIM(C)={{x1}，{x2，x6}，{x3}，{x4，x5}，{x4，x5，x6}，{x2，x5，x6}}；

U/SIM(C-{c1})={{x1，x2}，{x1，x2，x6}，{x3}，{x4，x5，x6}，{x4，x5，x6}，{x2，x4，x5，x6}}；

U/SIM(C-{c2})={{x1}，{x2，x6}，{x3}，{x4，x5}，{x4，x5，x6}，{x2，x5，x6}}；

U/SIM(C-{c3})={{x1}，{x2，x6}，{x3}，{x4，x5}，{x4，x5，x6}，{x2，x5，x6}}；

U/SIM(C-{c4})={{x1，x3}，{x2，x3，x6}，{x1，x2，x3，x6}，{x4，x5}，{x4，x5，x6}，{x2，x3，x5，x6}}；

U/SIM(C-{c5})={{x1}，{x2，x6}，{x3}，{x4，x5}，{x4，x5，x6}，{x2，x5，x6}}；

sigC(c2)=D(C，C-{c2})=0；

sigC(c3)=D(C，C-{c3})=0；

sigC(c5)=D(C，C-{c5})=0.

求得B=core(C)={c1，c2}，由于D(B，C)≠0，所以计算

sigB∪{c2}(c2)=0；

使得B=B∪{c3}，此时D(B，C)==0，算法结束，求得约简为{c1，c3，c4}.

根据求得的约简结果得到了新的信息系统U'={x，x2，x3，x4，x5，x6}，C'={c1，c3，c3}，D'={c6}.

(2)对新的信息系统(U'，C'∪D')求决策规则，可得:

r1:(Price，high)∧{Power，medium}∧(Size，full)→(Quality，good);

r2:(Price，low)∧{Power，medium}∧(Size，full)→(Quality，good);

r3:{Power，medium}∧(Size，compact)→(Quality，poor);

r4:(Price，high)∧{Power，high}∧(Size，full)→(Quality，good);

r5:{Power，high}∧(Size，full)→(Quality，excel);

r6:(Price，low)∧(Size，full)→(Quality，good).

(3)对求出的6个决策规则进行合并，可得:

r'1:((Price，high)∧(Power，medium)∧(Size，full))∨((Price，low)∧(Power，medium)∧(Size，full))∨((Price，high)∧(Power，high)∧(Size，full))∨(Price，low)∧(Size，full)→(Quality，good)；

r'2:(Power，medium)∧(Size，compact)→(Quality，poor)；

r'3:(Power，high)∧(Size，full)→(Quality，excel).

以上获取的三条规则即为相对最优决策规则.

4 结语

本文通过基于知识距离提出的约简算法，针对不完备信息系统，提出了一种决策规则的提取方法，实例证明该方法求得的决策规则，能有效地分析和处理含有缺省数据和不精确数据的信息系统，扩展了粗糙集的应用领域.

参考文献：

[1]Z.Pawlak.Rough Sets-Theoretical Aspects of Reasoning about Data[M].Dordrecht，Boston，London:Kluwer Academic Publishers，1991.

[2]何明，傅向华，马兆丰.基于不完备信息系统的Rough Set决策规则提取方法[J].计算机应用，2003，23(11):6-8.

[3]张文修，吴伟志，梁吉业，李德玉.粗糙集理论与方法[M].北京:科学出版社，2001.

[4]J.Y.Liang，Z.Z.Shi，D.Y.Li，M.J.Wierman.Information entropy，rough entropy and knowledge granulation in incomplete information systems[J].International Journal of General Systems，2006，35(6):641-654.

[5]曲开社，翟岩慧，梁吉业，李德玉.形式概念分析对粗糙集理论的表示及扩展[J].软件学报，2007，18(9):2174-2182.

[6]史琨.粗糙集的知识获取方法研究[D].太原:山西大学，2009.