基于最优化的机器人避障路径规划的研究
田 敏,吴瑞溢
(黎明职业大学 公共教学部,福建 泉州 362000)
1 问题的提出
机器人技术作为20世纪人类最伟大的发明之一,自60年代初问世以来,从简单机器人到智能机器人,机器人技术的发展已取得长足进步.机器人避障路径规划是机器人应用中的一项重要技术[1-3].使用良好的避障路径可以节省大量机器人作业的时间,同时也可以节约人力资源,减小资金的投入.避障路径规划典型的描述是:在有障碍物的环境中,如何寻找从起始点到目标点的运动路径且无碰撞地通过所有障碍物.本文具体分析如下问题.
图1是一个800×800的平面场景图,在原点O(0,0)点处有一个机器人,它只能在该平面场景范围内活动.图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物,障碍物的数学描述如表1.
在图1的平面场景中,障碍物外指定一点为机器人要到达的目标点(要求目标点与障碍物的距离至少超过10个单位).规定机器人的行走路径由直线段和圆弧组成,其中圆弧是机器人转弯路径.机器人不能折线转弯,转弯路径由与直线路径相切的一段圆弧组成,也可以由两个或多个相切的圆弧路径组成,但每个圆弧的半径最小为10个单位.为了不与障碍物发生碰撞,同时要求机器人行走线路与障碍物间的最近距离为10个单位,否则将发生碰撞,若碰撞发生,则机器人无法完成行走.


表1 障碍物特性表
建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型.对场景图中4个点O(0,0),A(300,300),B(100,700),C(700,640),具体计算:(1)机器人从O(0,0)出发,O→A、O→B、O→C和O→A→B→C→O的最短路径;(2)机器人从O(0,0)出发,到达A的最短时间路径.
2 问题的分析
路径规划属于组合优化的范畴.典型的方法有单源最短路径的Dijkstra算法、任意两点间最短路径的Floyd动态规划算法及智能算法等[4].但由于机器人避障问题的复杂性,常常使得传统的数学优化方法显得无能为力.因此直接去寻找最优避障路径是不太现实的,我们基于最短路径算法的思想,在路径规划过程中,先分析相邻的两个障碍物之间及目标点到邻近的障碍物之间的路径,使其局部优化,然后综合结果,采用Floyd算法逼近最优路径.
3 机器人避障的局部路径优化模型
为便于讨论,同时降低问题的复杂性,我们首先根据机器人路径的行走规则,对机器人避障路径进一步做一些说明,得到以下结论.
结论1 机器人的行走路径由直线段和圆弧组成,圆弧所在的圆必会覆盖多边形的顶点.
说明:若障碍物在两个目标点中间(连线与障碍物相交),我们用矩形障碍物为例加以说明,A、B为目标点,中间是矩形障碍物,如图2.
从A到B绕过矩形障碍物的路径有无数多条,但由于两点之间直线最短,以及三角形两边之和大于第三边,如图2,容易知道走路径ADB的方式较佳,说明了结论1的正确性.
结论2 机器人从目标点绕过障碍物顶点的局部最优避障路径为:以障碍物的重心点和顶点连线的直线段上某一点为圆心,并以圆心到障碍物顶点的长度再延长10个单位为半径作圆,作目标点到该圆的切线,目标点到圆的切线与切点到中心直线与圆交点的这段圆弧即为局部最短路径.
说明:为便于讨论,我们同样以矩形障碍物作说明,如图3.

图1 800×800平面场景图

图2 目标点到障碍物的最佳路径

图3 目标点到障碍物的局部最优路径

图4 障碍物到障碍物的局部最优路

在结论2的基础之上建立机器人从目标点绕障碍物的局部最优避障路径模型,计算从目标点绕过障碍物顶点的局部最优路径长度,以图2为例,记A(xA,yA),D(xD,yD),重心点Q(xQ,yQ),先不考虑机器人的行走速度,根据结论2的作法,建立模型,确定局部最优避障路径.
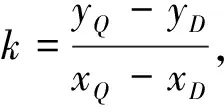
yP-yD=k(xp-xD)
(1)
又|PD|=ρ-10,故
(2)
由(1)、(2)得
由三角形DPA得


综上,机器人从目标点A绕过障碍物顶点D的局部避障路径为:|AB|+θρ,局部最优避障路径模型如下:
min |AB|+θρ
s.t.ρ≥10
(3)
又已知机器人直线行走的最大速度为V0.机器人转弯时,最大转弯速度为v=v(ρ),在上述(3)的基础之上容易得出机器人从目标点绕过障碍物顶点的局部最短避障时间路径:
结论3 机器人从一个障碍物的顶点绕过另一障碍物顶点的局部最优避障路径为:分别以两个障碍物的重心点和顶点连线的直线段上某一点为圆心,并以圆心到障碍物顶点的长度再延长10个单位为半径作圆,作两圆的切线,这两个圆的切线段与两个切点分别到重心直线与圆交点的两段圆弧即为局部最优路径.

根据结论3建立机器人从一个障碍物顶点绕另一障碍物顶点的局部最优避障路径模型,计算从障碍物到障碍物的局部最优避障路径长度,如图4所示,记A(xA,yA),B(xB,yB),矩形的重心点为(x1,y1),三角形的重心点为(x2,y2).先不考虑机器人的行走速度,根据结论3的作法,建立模型,确定从一个障碍物的顶点绕过另一障碍物顶点的局部最优避障路径.

(4)
直线PA方程为:y-yA=k1(x-xA),将点P代入方程得
yp-yA=k1(xP-xA)
(5)
又|PA|=ρ1-10,故
(6)
(7)
由(4)所构三角形得
(8)
由(7)、(8)及图3得θ1=

综上,机器人从障碍物顶点A绕过障碍物顶点B的局部避障路径为|EF|+θ1ρ1+θ2ρ2,局部最短避障路径模型如下:
min |EF|+θ1ρ1+θ2ρ2
s.t.ρ1,ρ2≥10
(9)

s.t.ρ1,ρ2≥10.
4 机器人避障的Floyd路径优化
通过局部路径优化的分析,我们把机器人避障问题归结为最短路问题,现在只需要把各个凸障碍物的顶点延长10个单位(障碍物2为圆不必处理),然后利用局部避障优化模型,借助matlab优化工具箱[5]分别计算每相邻两个顶点的局部最优解作为权值,不相邻的两个顶点则记为无穷大.
对场景图中4个点O(0,0),A(300,300),B(100,700),C(700,640),利用最短路算法Floyd[6-7]具体算得:(1)O→A机器人的最短避障路径长:474.3838,机器人从原点O(0,0)出发经过点(70,220),(240,50)到达A(300,300)为最短避障路径;(2)O→B机器人的最短避障路径长:869.5251,机器人从原点O(0,0)出发经过点(50,290),(150,445),(230,460),(230,540),(140,590)到达B(100,700)为最短避障路径;(3)O→C机器人的最短避障路径长:1093.9,机器人从原点O(0,0)出发经过点(420,90),(730,510),(730,610)到达C(700,640)为最短避障路径;(4)O→A→B→C→O机器人的最短避障路径长:2714.307,机器人从O(0,0)点出发经过点(70,220)(240,50)、A(300,300)、(230,540)、(140,590)、B(100,700)、(360,670)、(440,670)(530,740)、(680,740)、C(700,640)、(730,610)、(730,510)、(420,90)再回到O点为最短避障路径;(5)机器人从原点O(0,0)出发经过点(64.69,203.13)(86.54,225.75)到达A(300,300)为最短时间路径,总时间为:94.13(s).
5 模型的评价
本文将复杂的机器人避障路径规划问题合理的转化为最优化问题来求解,通过局部优化路径模型,我们只需求一元函数和二元函数的最小值,这样就把最优化跟Floyd最短路径算法有效的结合起来.然而,若问题中出现大量的障碍物数量以及不规则形状,就会导致顶点大大增多,再要借助最优化的方法来计算就会显得繁琐,这是需要改进的地方.
参考文献:
[1]J.H.Reif.J.A.Storer.Shortest Paths in the plane with polygonal obstacles[J].Journal of the ACM(JACM),1994,41(5).
[2]周智,陈国良,顾钧.用O(tlogt)的连接图求有障碍时的最短路径[J].计算机学报,1999,22(5).
[3]严寒冰,刘迎春.基于GIS的城市道路网最短路径算法探讨[J].计算机学报,2000,23(2).
[4]孙增圻.智能控制理论与技术[M].北京:清华大学出版社,1997.
[5]张圣勤.Matlab 7.0实用教程[M].北京:机械工业出版社,2006.
[6]何清林.Floyd算法的景区最短路径查询系统的设计与实现[J].电脑编程技巧与维护,2010(01).
[7]石为人,王楷.基于Floyd算法的移动机器人最短路径规划研究[J].仪器仪表学报.2009,30(10).

