实Clifford分析中双k超正则函数的等价条件
彭维玲,刘天云
(通化师范学院 数学学院,吉林 通化 134002)
Clifford分析是上世纪70年代新兴起的一个数学分支,具有重要的理论和应用价值[1-2].2003年,Eriksson-Bique和Leutwiler在修正的Dirac算子的基础上,首次引入了k超正则函数,并讨论了它的性质,受到了广泛的重视[3].本文在给出了实Clifford分析中双k超正则函数的定义基础上,借助黄沙的拟置换思想[4],给出了双k超正则函数的一个等价条件,建立了双k超正则函数与偏微分方程组的联系.
1 预备知识

Ap+1(R)的任一元素可唯一地分解成a=b+cep+1,这里b,c∈Ap(R),称b为a的P部,称c为a的Q部,记为Pa=b,Qa=c.

引入Dirac算子D:
(1)




(2)
则称f(x,y)为Ω上的双正则函数.
引入修正的Dirac算子:
(3)

(4)
则称f(x,y)为Ω上的双k超正则函数.
特别地,当k=0时,f(x,y)为双正则函数,当(4)式第一个k=p-1且第二个k=q-1时就是双超正则函数.
2 主要结论
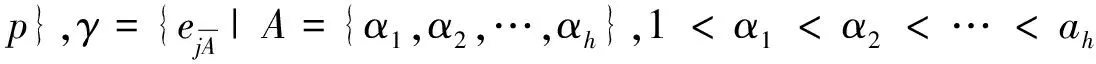



(5)
证明






因此,(5)式得证.
参考文献:
[1]Brackx F,Delange R,Sommen F.Clifford Analysis(Research Note in Mathematics76)[M].London:Pitman,1982.
[2]Ryan J.Clifford algebra and their applications in mathematical physics[M].Berlin:Birkhäusr,2000.
[3]Sirkka-Liisa,Eriksson-Bique.k-Hypermonogenic funcations[J].In Progress in Analysis,World Scientific,2003(1):337-348.
[4]黄沙.拟置换与实Clifford分析中的广义正则函数[J].系统科学与数学,1998,18(3):380-384.

