V型带传动的传递功率损失第Ⅱ部分：小带轮半径的影响（一）

T H C Childs D Cowburn

符号

Notation

A ｛Gd/（ct）｝1/2

B，H 带顶宽度和厚度 V－belt top width and depth

c 带伸长模量 belt extension modulus

d 平带宽度 flat belt width

EI 带变曲刚度 belt bending stiffness

F 带拉力和特定值 belt tension force；particular values are Ft，Fr，FA，FB

gand g180γ＝180°带径向屈服 belt radial compliance forγ＝180°

g0，g90分别γ＝0°和90°带径向屈服 belt radial complicance forγ＝0°and 90°respectively

G 带体剪切模量 belt carcass shear modulus

k0，k1V 型带径向屈服参量 V－belt radial compliance parameters

M 带固有弯矩特定值 belt internal bending moment；particular values are MA，MB

p 带和带轮接触压力 belt/pulley contact pres－sure

pz带轴向内应力 V－belt axial internal stress

Q 带因弯曲的内剪切应力特定值为QA，QBbelt internal shear stress due to bending；particular values are QA，QB

R 在带节圆带轮半径 pulley radius at the belt pitch circle

S0gEI/R4

S1｛g/（EI）｝1/2F

t 平带厚度 flat belt thickness

T，ΔT 转矩和速度损失 torque and torque loss

u 带径向位移特有值为uFbelt radial displacement；particular value is uF

U u/R 和特有值UF＝uF/R u/Rwith the particular value UF＝uF/R

UndnU/dφn和特有值UnA，UnBdnU/dφnwith the particular values UnA，UnB

α 接触弧 are of contact

2β V型带轮槽角 V－pulley groove angle

γ V型带滑动角 V－belt sliding angle

μ 摩擦系数 friction coefficient

ρ 带半径 belt radius

φ，Ψ 角变量 angular variables

φA，φBV 型带入口和出口接触弧 V－belt entry and exit contact arcs

1 前言

为汽车发生辅助功率采用交流发电机转子可以高于发动机最大转速的角速度转动，在该功率发生中利用V型带驱动发电机带轮，带轮半径必须小于曲轴的带轮。功率传递到交流发电机通常限制于主动V型带弯曲不过早失效的最小半径。

本文在上篇述及的因带在带轮槽内失配对效率的影响（1），接下来阐述V型带带轮半径对功率损失的影响。希望简要导出可良好模拟带在小半径带轮上的内部变形，从而很好理解失效。AV10缠绕带，毛边带和齿带已用于传递带轮半径为51，36和21mm的带轮间的功率，其最后一带轮半径小于这些带所推荐的最小半径28mm。已发现带速和转矩两者损失较理论预测快速随带轮半径减少而增大。准备把一些相似AV10毛边带的矩形带和圆柱带轮匹配运转，它们的功率损失意外的和V型带相同。因此推荐损失机理通常应归因于带的V型种类而全部没有特殊之处。

在等半径带轮间传递功率时，摩擦功率损失可认为是摩擦速度或滑移运动和摩擦转矩损失两项之和。随着转矩的改变，结果发现有一个转矩造成了最大值的传动效率。在小于最佳的转矩，转矩损失占主要部分，在最大值，速度损失增加至带打滑，可传递的功率受到了限制。这里概述在低转矩，开始打滑和转矩损失的速度损失原理，以后和实验结果比较。

2.1 低转矩速度损失

文献［1］已概述了这里测试的有关功率损失理论。在低转矩，带和带轮间圆周滑动接触内的作动弧小于总接触弧，此时的摩损速度损失是因拉伸件或伸长模量C带的伸长造成的，摩擦速度损失是由带在带轮槽内径向运动造成，它与转矩成比例。可给出表明摩擦速度损失的算式为

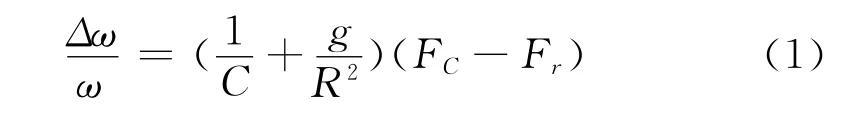
式中g是带在带轮槽内的径向屈服，R为带轮半径和Ft及Fr是带索内因传递转矩T：（Ft－Fr）R＝T引起的拉力。

理论导出的公式（1），因为带和带轮在接触区没有圆周滑动，故假定带拉伸组件和带轮在该区角速度相等。然而拉伸件和带轮被带体分开，这里许可没有滑动的拉伸件和带轮间有一点角速度的差异。Firbank（2）在这方面已对平带进行了研究，结论表明有关V型带方面下次研究。他已表明传递转矩考虑到带体剪切，但没有作动打滑，接触的进一步推导。相关速度损失也和Ft－Fr成比例，但上述一临界转矩一作动弧推导算法，速度损失增加比Ft－Fr快速，虽然速度损失与Ft－Fr成比例，但它进一步｛Gd/（ct）和接触弧α以及带的特性参量 这里写为A有关，其中G是带体的剪切模量，d和t分别是带体的宽度和厚度，它的研究推导给出

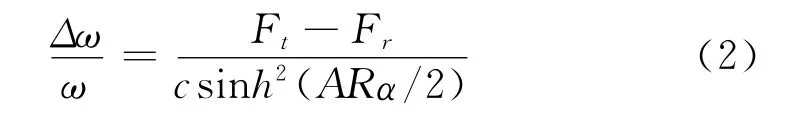
该式值得注意的关系是延伸速度损失作为ARα/2，小于1。形成的sinh项导致速度损失与R2成反比，相同于式（1）内由于径向运动的速度损失，随接触弧减小而增大。

2.2 过渡到滑移运动

初步分析预测可存在于带轮周围的最大拉力比（Ft/Fr），径向和周向力平衡作用于平带的作动弧，得出带拉力F和角位置中的差分方程为

式中μ是带和带轮间的摩损系数，当作动弧包覆整个接触弧α时，式（3a）积分得出大家知道的绞盘公式

对于－V型带，假定在楔入带轮槽的作动弧内周向滑动，得

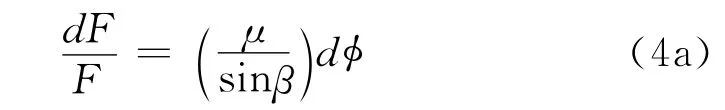
式中β为槽的半角，那么

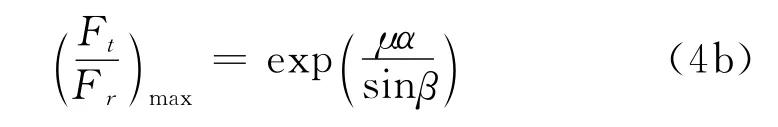
当转矩相应于（Ft/Fr）max时，速度损失不再近似与转矩成比例。并以不断增大速率增加减小滑移运动。采用用一个实际的带和带轮组合限制，可引用一（Ft/Fr）作为最大值，稍小于（Ft/Fr）max。

对于这样限制的一个最小值，它应偏离线性的速度损失和刚起动的转矩。对于平带应包括带体内剪切的研究［2］，这点在最后部分讨论。在V型带分析方面忽略了这样剪切，当作动弧首次包覆整个接触弧时，假定为非线性起动。在该阶段，Ft/Fv小于式（4b）的最大值，因为在推得的式（4a）中忽略了带在作动弧的径向运动。

径向运动的模拟和其对作动弧拉力比的影响，已经由许多作者（3～8）作了推算，但以Gerbert（8）更详尽。在作动弧径向和周向滑动组合导致一种情况，槽在带上生成的摩擦力不在圆周方向。Gerbert表明式（4a）应修正为

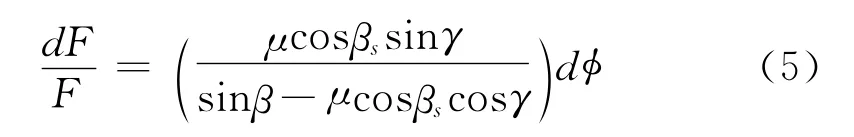
式中γ是摩擦力方向在带中间面上投影和带轮向内指向径向之间的夹角，βs修正γ的影响。考虑到事实上摩擦力方向在带轮槽表面的平面内而不是在带的中间面内，所以

tanβs＝tanβcosγ

当γ＝90°（无径向运动），式（5）简写为（4a）。但当γ＝180°或0°时（带运动分别为单纯向内或向外），式（5）表明F和φ不变。

一般γ围绕作动弧变化，式（5）积分得出Ft/Fr，要求对带和带轮间的相对运动作仿真研究，变成要求模拟带在带轮槽内的位移。当然该周向位移随F改变由于带拉长与C有关。然而径向位移不仅与F同时也与γ有关。图1示带在一槽内的半截面。

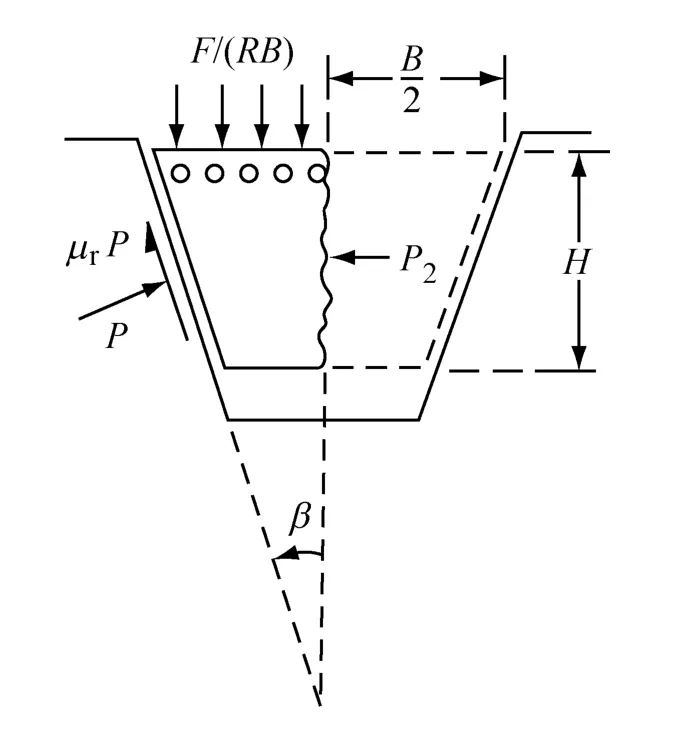
图1 V型带截面Fig.1 A V－belt section

在带帘布上的拉力。造成一分布的每单位宽度的径向力F/（RB），在带体顶部径向向内作用，一轴向压力Pz作用带体中面，法向力和摩擦应力p和μrp作用于带轮表面。一般摩擦力不作用在图平面，而是μ的分力μr作用在图平面，μr小于μ，它依据于r由＋μ变到－μ。Gerbert建议Pz造成带体的轴向压缩，把带插入槽内，当F/（RB）通过泊松比影响造成带轴向伸长时，带升出槽外。带由节圆半径的径向位移u可以考虑是这些影响的综合，分别与Pz和F/（RB）成比例。以后研究由图1内水平和垂直平衡确定Pz和F/（RB）之间的关系。

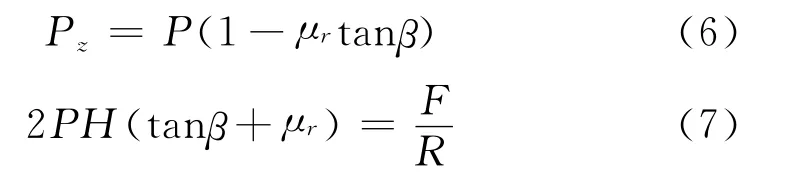
Gerbert推荐

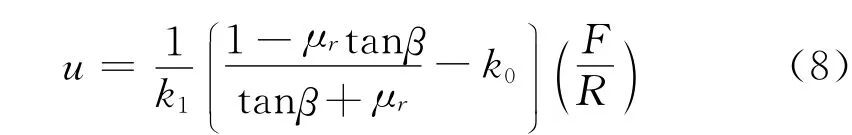
式中常数k1和k0可由文献［9］模拟或由实验求得。在以下实验处理方面，在缺乏任何圆周滑动，加载使带进入带轮槽内（当ur＝u时）以及在完全滑移运动（当ur＝0时）测得的，u随F/R变化。采用式（8）两种形式求解k1和k0。μ本身由滑移试验和用式（4b）求得，［式（8）內左边乘以 F/R 则与式（1）的径向屈服g相同，似乎可认为g与γ有关。把g看成对于γ＝180°，g在式（1）内更精确。］

Gerbert（8）积分式（5），包含带在带轮槽内运动的影响，表明起动非线性速度损失Ft/Fr与无因次带和带 轮 特 性 C/（k1R2），ks，μ，β 和α 以 有 C/（k1R2）有关，实际上带在带轮上径向的圆周运动的这个比值增大，或改变带的特征或减小带轮半径计算该比值Ft/Fr降低。它可能小于exp（μα）。对于平带预测该值，为加强带的控制，用槽的楔合作用，完全用径向运动补偿。这种影响从动比主动带轮更大。在本文中重复了Gerbert的计算并和实验比较。

在最近Gerbert的论文（10）中建议，采用一较大的Ft/Fr值大于作为实验限制用于的－V型带采用在起始的非线性速度损失。某些Ft/Fr值，在非线性滑动状态，γ通常随作动弧变化，成为一常数。在该阶段，Gerbert要求限制非线磨损，那么容易计算Ft/Fr。这点已在本程序中重复，并将讨论作为一设计极限。

2.3 转矩损失

实验发现在转矩传递中V型带的转矩损失变化不大，它们有两种情况：带在带轮上或离开弯曲造成的滞阻损失，和带进入和脱离啮合时，带楔入或离开带轮槽的滑动损失。滞阻损失可预测为随EI/R改变，其中EI是带的弯曲刚度；缺乏实验监测，它似乎表明只近似与1/R有关（11）。滑动损失随Ft＋Fr增大（1，11）。

带进入和脱离啮合的滑动造成转矩损失，是因为滑动方向相反由γ＝180°到γ＝0°，引起带从脱离到进入时径向屈服不同。因而带在带轮槽的行程在不同的两区间，由于带的弯曲和剪切带在带轮上的反转矩不同。

带在作动弧的行程分析概述于下节，不恰当地假定在进口和出口区带的半径值限于和带轮接近。随着位置变化很小，因而在行程上忽略带刚度的任何影响。但在进口和出口区带的刚度是不能忽略的，由于带轮在小的弧度接近无限小带的半径改变，Gerbert已发表（11）了这些区域的数值分析文章。他介绍了他的图解结果，表明无因次转矩损失或功率损失ΔT/（R3k1）与无因次带拉力F/（R2k1），无因次刚度EI/（R2k1）以及μ有关。他表明了参量C/（R2k1）和k0在作动弧上的影响性质，在进口和出口区有小的影响。

本文认为Gerbert建议的无因次变量的选择不是最好的。他的分析图表可以写成转矩损失的表达式，对于等半径带轮传动情况，μ≤0.4，可写成

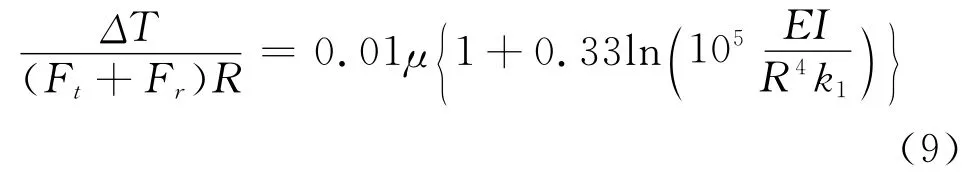
对于μ≥0.4，转矩损失几乎与μ无关，可以把μ＝0.4代入式（9）求得。在下节将介绍本文的试验结果，并表明了进口和出口区的简化分析方法，其中出现的正常无因次变量如ΔT/（FR），（gEI/R4）1/2，（其中g是γ＝180°的径向屈服），｛g/（EI）｝1/2和μ。

3 一近似的滑动转矩损失原理

作为小转矩传递的转矩损失，这里考虑最简单的零转矩传递情况，此时Ft＝Fr。图2a示一带在带轮槽内，其槽进口是A和出口为B，两者离开带轮中心O的节圆半径为R，A和B之间转角范围为φA和φB，在该处带嵌入或升出带轮槽，径向位移u随φ变化到一最大值uF，由式（8）给出μr＝μ。可方便导出无因次位移U＝u/R：

式中g180指为γ＝180°的g。

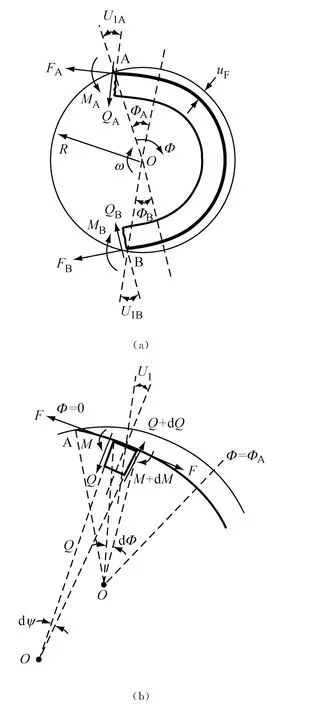
图2 带绕带轮的行程（a）一般视图（b）入口区详图Fig.2 The belt path round its pulley：（a）ageneral view and（b）entry region detail

U1A和U1B是带轮半径和在A和B带法线间夹角，由在A和B的du/dφ给出。由拉力FA和FB，剪力QA/QB，和弯矩MA和MB造成的带轮上的转矩，等于转矩损失ΔT，当FA＝FB＝F时，以后扩展Sin U1为U1和Cos U1为1－U21/2，

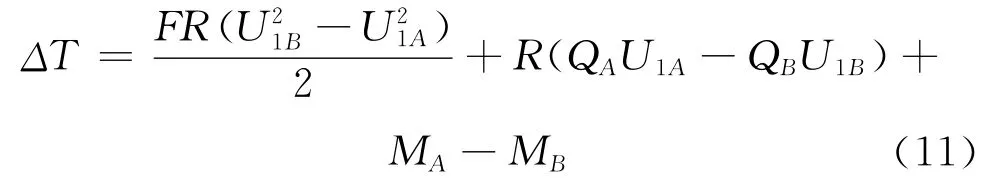
两等带轮半径之间的功率传递的功率损失是它的两倍。

Q，M和U1值在A和B是考虑带入口和出口的行程求得的，图2b示该入口区。带元件在O点对着dφ有一半径ρ＜R，在O′点对着dΨ。对于小的斜率，带在槽内U1和u≪R几何确定为

和

式中U2为d2U/dφ2。

带的法向力是平衡相等的，假定带和槽之间的滑动是径向的，U1是较小值，采有式（12）得：

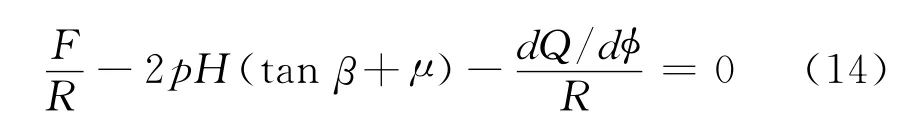
式中p见图1是在带轮槽上的接触压力。式（7）和（10）可采用与UF有关：

按转矩平衡和式（12）得

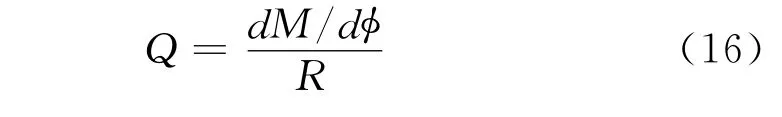
简化弯曲理论和式（13）得

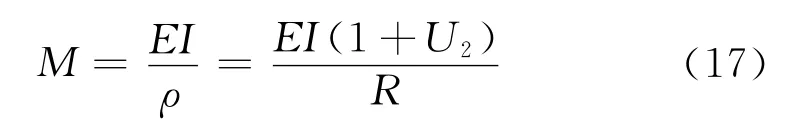
可变换式（14）对U 用式（10）和（13）把F 和Q代入第一项，用式（15）和差分方程式（17）和（16）代入第二项整理后得dQ/dφ的表达式

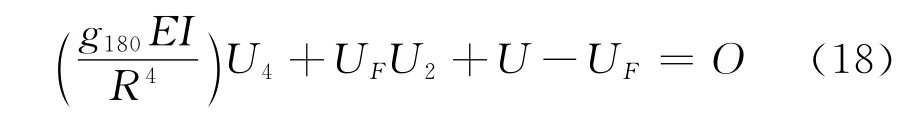
式中U4为d4U/dφ4。

该边界条件是φ＝0，U＝0，在该点带的自由跨距内，M和Q具有相同的数值。该自由跨距状况应展工：可如（8，12，13）所示，按转矩相等，几何和弯曲公式M＝EI/ρ，在自由跨距为

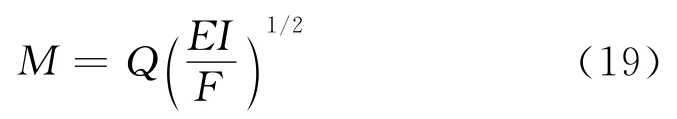
由式（17），（16）和（10）代入 M，Q 和F 得

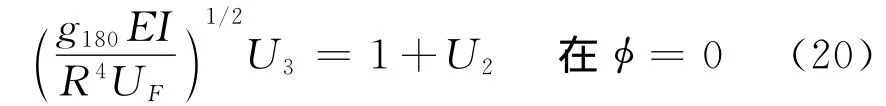
式中U3＝d3U/dφ3。

对（18）一个相同的公式可以对出口区展开，然而这里作为带离开槽滑动方向相反造成式（14）改变的中间项，以下式（15）对UFR/g0的形式，式中g0为γ＝0°时g，这种变更造成U的最终公式为

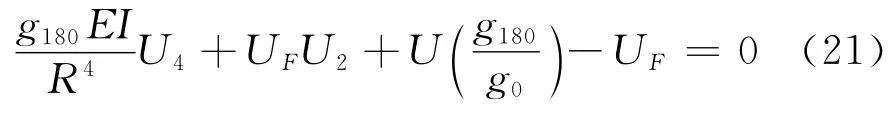
在φ＝0。相同的边界条件用于入口区，在φ＝φB附近，真实带特性必须比这更加复杂，这里推荐：滑动方向由γ＝180°至γ＝0°，超过一有限的弧并建议通过g＝g0区段则相反。由此可见已经造成一最简单的假定，为简单起见，在φB边界条件作为与在φA入口区相同。对U 解式（18）和（21），当在A和B用不同的U 和式（16）和（17）求出U1，Q 和M，代入式（11）求转矩损失。

由式（8）可见，分别或g180或g0可为负，对或μ＞（1－k0tanβ）/（tanβ＋k0）或μ＞tanβ，模拟导致式（8）为未定数，计算已求得转矩损失连续随μ增加导致符号改变。事实上，对于μ＞0.2，转矩损失几乎与μ无关，在文献［11］中更详细地与μ＞0.4作比较。

组合g180EI/R4可以写作S。在A和B数值计算 证明 U2/S1/40和U2仅与UF/S1/20有关。由式（10），同样对｛g180/（EI）1/2F｝将写作为S1，按此把式（16）和（17）代入（11），对于转矩损失由两等半径带轮可以表明，ΔT/（2FRS1/20）是S1和μ 的函数。图3a示μ＝0.2和S0由10－2至10－7的计算关系。它随μ的增加变化很小，用Ft＋Fr代替2F后，对于S1＞0.05，可认为是适合的。

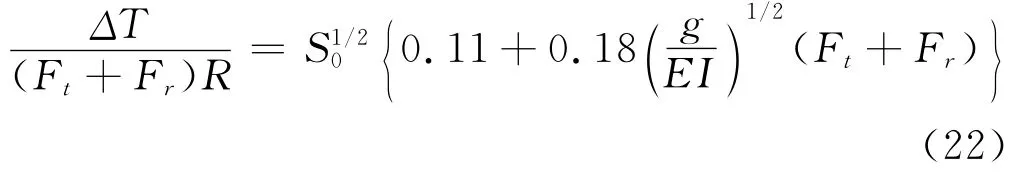
这里研究了在图3（b）中对AV10毛边带式（22）和（9）的计算比较，由式（22）算得的转矩损失小于式（9），但它们随1/R增加，式（9）几乎与R无关。

最后讨论由于带体剪切速度损失的可能性，式（2）表明接触弧展开角α与此有关。由带轮之间带的弓形该名义值将减少，在U1A由带进入和离开带轮将增大。弓形损失的早期分析（12）已考虑带首先与带轮接触的带轮半径R，并表明弓形损失在进口和出口是（EI/F）1/2/R。在本模拟中，已注明 A 和B带半径不等于R，但由式（13）给了的U2值是合适的。对于缺乏转矩传递中，名义接触弧π弧度，所以Ft＝Fr，可表明

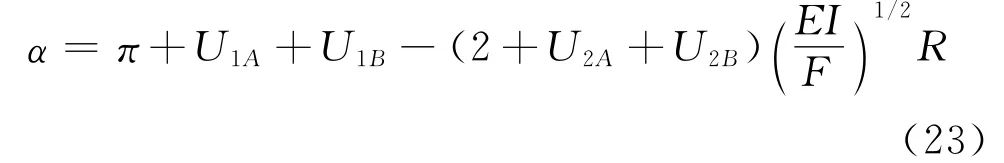
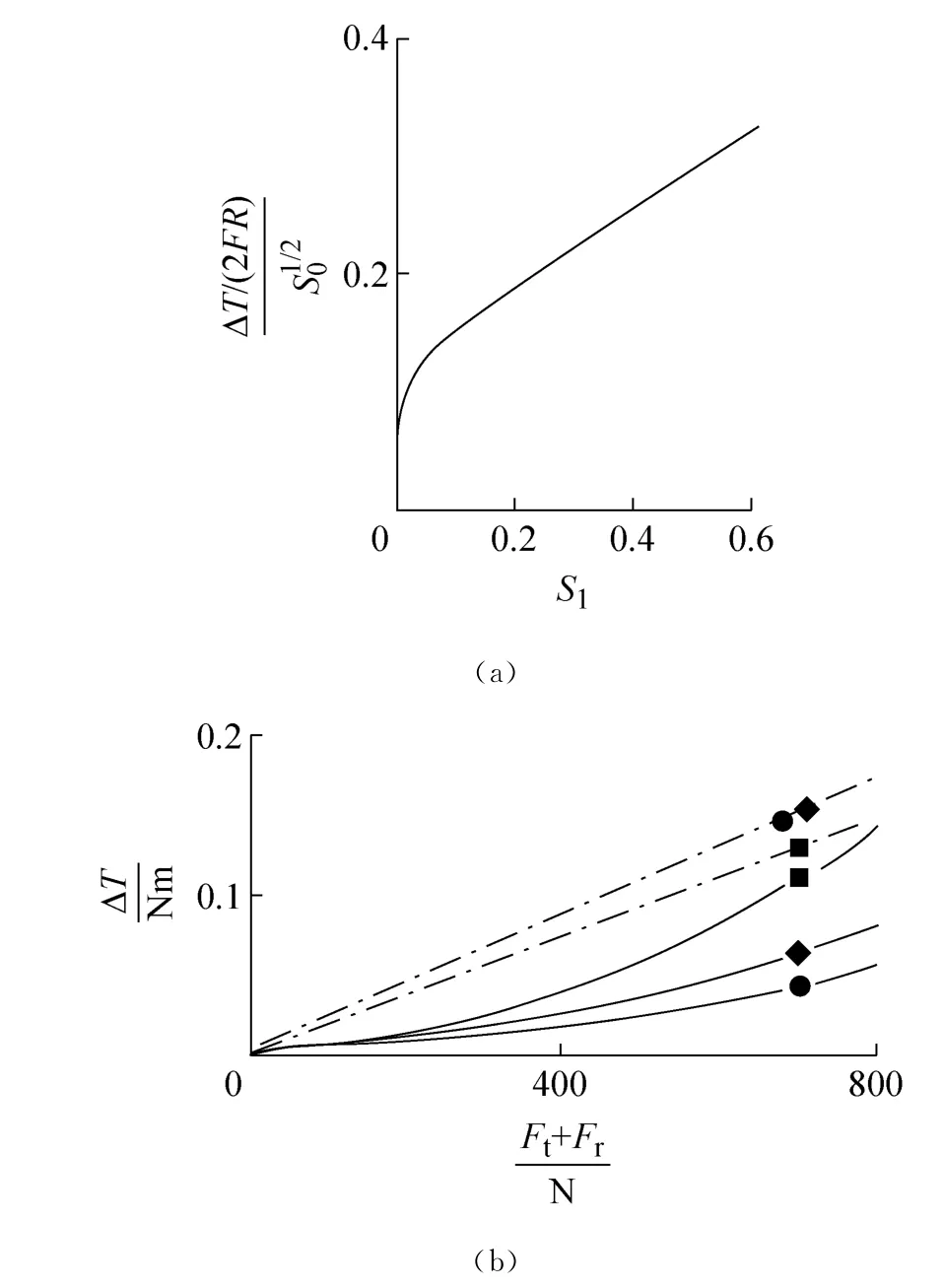
图3 （a）根据 ΔT/（2FR）计算无因次参量S0 和S1（b）对于AV10主边带在半径51mm（●），36mm（◆）和21mm（■）的数值实例，——式（22）和—·—·—式（19）采用μ＝0.4的预测Fig.3 （a）Calculated deperdance ofΔT/（2FR）on nondimensional parameters S0AND S1（b）A numerical example for AV10raw－edged belts on pulleys of radii 51mm（●），36mm（◆）and 21mm（■）：—— predications of equation（22）and—·—·—of equation（19）withμ＝0.4

对于式（22）的有效范围，以下经验适合于数值计算数据，已求得：

求得进口和出口角φA和φB为

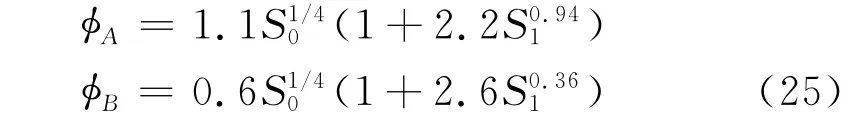
本预测与下节实验值相比较。

4 实验

两相等铸铁带轮安装于两相同的万向节架与直流分绕电机再生连接，传递功率时测量功率损失。该机器之一安装在滚动轴承上，在常总带拉力下进行试验。用仪器分别测量速度和转矩损失。采用的带总拉力为800N，转矩为20Nm和转速范围为600－6000r/m，已阐述文献［1］。

AV10毛边、缠绕和齿带以600－6000r/m在节圆半径为51，36和21mm的节圆上运转，在所有情况槽角均采用36°。在早期研究中可见，带和槽楔角间失配对功率损失的影响［1］。典型的带在试验前精确以0.5%的滑动运转至少8小时，直到损失不再随时间变化为止。在运转中，毛边和齿带楔角改变，摩擦力降低，尽管缠绕在21mm半径的带轮上包覆立刻由带体分离，对于该有限试验周期，带不能描述运转和以后表明的原因。

采用测量效率作为传递转矩的函数和带拉力直到打滑对机械的转矩的限制，获得性能的概观。再作低转矩传递下速度和转矩损失和开始时非线性速度损失的更详细的测量，同时还测量毛边带的实际接触弧和进口及出口区的角度。对于这些带是在玻璃带轮上运转，可直接观察其接触情况（1，14）。显示了进口和出口区接触间的接触压力，和接触度以及透明地观察到接触随角度位置快速变化。可确定典型的在±5°以内。

按与原始AV10毛边带相同制造了毛边矩形截面带，其带宽为10mm，厚8.1mm，带体5.8mm，帘布区2.3mm。在50mm半径的圆柱带轮上测量其速度和转矩损失，结果与V型带比较。某带体由帘布分开，测量带体和帘布分离的损失。最后一平带由一些冷拉尼龙带拉伸的标准平带制成（14）。它近似0.5mm厚度，并预期有一很小的转矩损失，在转矩损失校准中进行零误差检验。

如以前所述（1），采用静态获得C，EI和g180确定k0和k1［式（8）］测量带的变形特性。一带在试验中静态支承在慢速转动的带轮槽内，接触弧为40°，滑动速度由10至100mm/s。从带的接触弧的一端挂重测量用弹簧平衡的另一端来确定带的拉力。采用卷筒计算式（4a）估算接触弧中点带的拉力，这里安装一千分表测量拉力改变时带的径向移动距离。

采用通过接触弧的拉力比按式（4b）计算摩擦系数，假定垂直于带体加强纤维方向测量1/3杨氏模量，这是根据带的静态拉伸和弯曲试验获得的，根据矩形带体在平带轮上运转的速度损失测量得到的杨氏模量为C和带的横截面积。

5 结果

5.1 一般观察

图4示对于毛边和齿带在三个半径不同的带轮上和一总的带拉力范围运转，效率随转矩传递的变化情况，没有表明缠绕带的结果，采用51mm半径的带轮，试验仅进行到打滑状况，结果与毛边带十分接近。

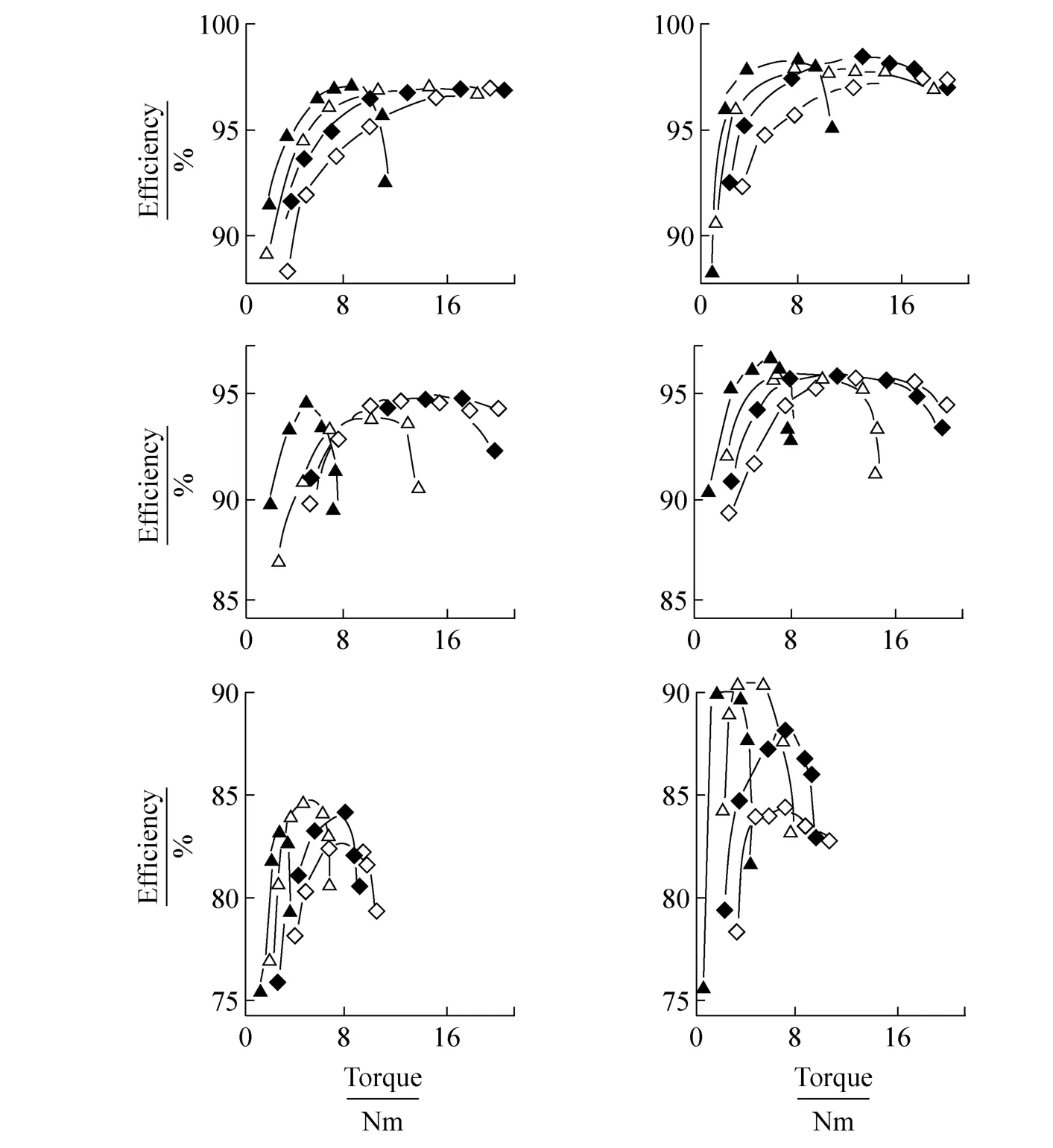
图4 效率随传递转矩变化图对于毛边带（左列）和齿带（右列），AV10带在带轮半径51mm（一行），36mm（二行）和21mm（三行），在总带拉力200N（▲），400N（△），600N（◆）和800N（◇）Fig.4 The variation of efficiency with torque，transmission for raw－edged（left column）and cogged（right column）AV10belts on pulleys of radii 51mm（row 1），36mm（row 2）and 21mm（row 3）at total belt tensions of 200N（▲），400（△），600N（◆）and 800N（◇）

显然可以看到最大效率的最佳转矩，其值随带的拉力和带轮半径变化。在低转矩，效率因转矩而下降，作为转矩降低而转矩损失保持为常数。在高转矩，较大的滑动降低了效率。同时还看到带拉力的最佳范围大约为400－600N。在较低的拉力下，滑动使可传递的转矩降低，在高拉力下，造成过多的转矩损失。

减少带轮半径，峰值效率和转矩传递范围降低。对于毛边带，带轮半径为51，36和21mm时，峰值效率将分别是97%，94.5%和85%，对于齿带相应值为98%，96%和90%。因而最小百分比功率损失，对于毛边比齿形带，在百分比效率和100%之间不大于1.5倍。只有在低的带拉力下，齿形带比毛边以更大的效率运转。考虑一极端的实例，在最大的总带拉力800N的带在21mm半径带轮上运转，齿形带的峰值效率降到84.5%，毛边带为82.5%。

5.2 传递低转矩的速度和转矩损失

在线性速度损失条件下，摩擦速度和转矩损失随拉力差（F0－F1）和总拉力（Ft＋Fr）变化的典型监测如图5所示。图5a证实了Δω/ω随Ft－Fr变化，但观察到的是随Ft＋Fr梯度增加而不像式（1）的预期。图5（b）示转矩损失与Ft－Fr无关而是随Ft＋Fr增加。

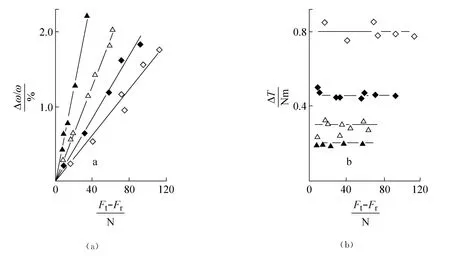
图5 （a）Δω/ω和（b）ΔT对Ft－Fr 的关系线图对于－AV10毛边带在21mm半径带轮上总拉力100N（▲），200N（△），400N（◆）和800N（◇）Fig.5 The dependence of（a）Δω/ωand（b）ΔT on Ft－Frfor an AV10raw－edged belt on 21mm radius pulley at total belt tensions of 100N（▲），200（△），400N（◆）and 800N（◇）

采用所有三种带型在所有三种半径带轮上获得图5所示的结果，（Δω/ω）/（Ft－Fr）和ΔT与 Ft＋Fr的关系集中于图6a和b。图6a示摩擦速度损失随带拉力减小而增大，这在小半径带轮半径上比大半径带轮增加更大，带类型（在AV10技术规定内）的影响小。水平链线是式（1）载荷独立预测，以后研究。图5（b）示转矩损失随Ft＋Fr线性增加，增加比率大于理论预测，如图3b所示。采用零总带拉力对于带是滞后损失的推断求得非零转矩损失。带型间的主要差别是齿带的滞后损失约为0.03至0.07Nm，同样如果带轮半径从51减至21 mm，与缠绕带和毛边带比较约为0.10－0.14N·m。

5.3 转矩传递范围

实际上最重要的是要了解不会引起效率大大降低这一缺陷可传递的最大转矩。理论上可看到，推荐过渡到打滑的转矩是低估，在该时是非线性速度损失开始。本实验表明，对于Ft＋Fr≥100N在非线滑动开始，Ft/Fr几乎与Ft＋Fr无关。图7示毛边带它与带轮半径有关。图7同时标明Ft/Fr与上述转矩相符合的大值。实际引起效率大为降低。在图4由毛边带求得该临界转矩，例如采用36mm半径带轮在Ft＋Fr＝400或600N时该临界转矩为12和17Nm；对于采用21mm半径带轮在同样的拉力下为6和8N·m。

图7阴影区表明 Gerbert预测的（8，10）Ft/Fr的非线性和弱非线性限制值，该区间宁可为一直线，因为用于它们的计算（表1）中，在带变形特性方面，实验的确定性。可以看出，弱非线性限制对于半径大于50mm的带轮是一个安全设计界限，但对于较小半径带轮设计是不安全的。对于21mm半径带轮，该非线性极限刚安全。

图6 对于毛边带（左列）缠绕带（中列）和齿带（右列）的AV10带在带轮半径51mm（●），36mm（□）和21mm（◆）（a）（Δω/ω）/（Ft－Fr）和（b）Δ与Ft＋Fr 关系Fig.6 The dependence of（a）（Δω/ω）/（Ft－Fr）and（b）ΔT on Ft＋Fr，for raw－edged（left column），wraped（middle column）and cogged（right column）AV10belts on pulleys of redii 51mm（●），36mm（□）and 21mm（◆）

5.4 接触弧观测

图8示毛边带有效的接触弧在零转矩传递时如何随总带拉力和带轮半径变化，有效接触弧长限定小于入口和出口区间总弧长。实线是式（23）至（25）理论计算获得的，可以看到理论和实验很好吻合。然而必须标明，接触弧入口和进口区独立测量，实验和理论不能很好一致。式（23）和（24）低估了接触弧总长，和式（25）对入口和出口伸展一样，但这样差异在计算有效弧长时可以忽略。

图8和图6a之间观察到速度损失的这种相反关系将以后讨论。

5.5 平带试验

图9a主要表明对于矩形截面带在50mm半径平带轮上运转，Δω/ω如何随传递转矩变化。所述包括比较是对于Ft＋Fr＝100，200和400N。对于两种带的线性速度损失范围内的梯度是相同的，但根据V型带的楔入作用，预测该线性极限转矩，V型带大于平带。速度损失的结果表明，矩形带帘布和带体分布，试验仅在线性速度损失范围内运转。根据带体较大，帘布速度损失小于全带。

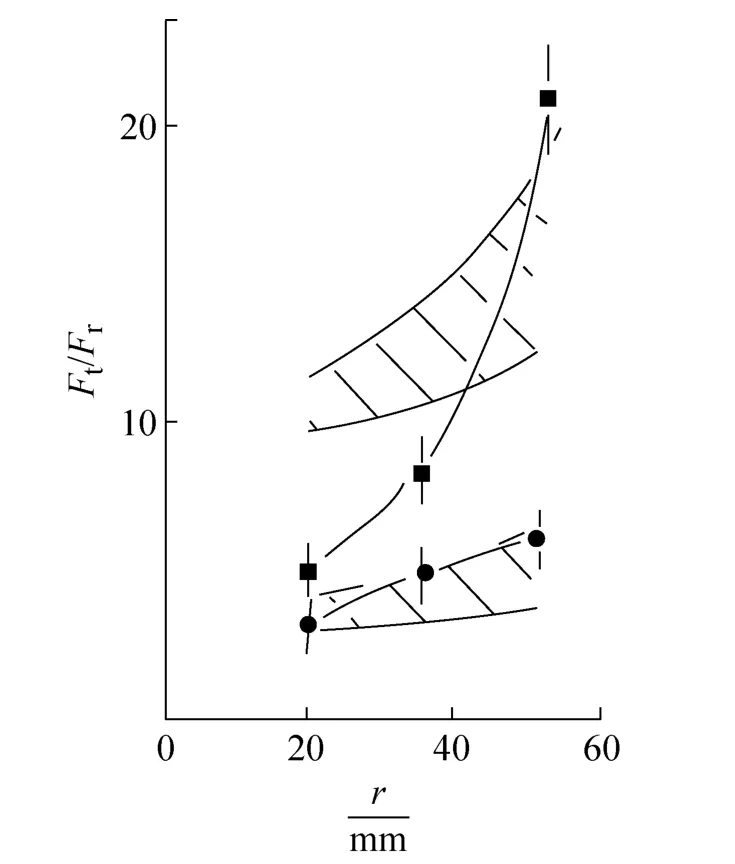
图7 测量Ft/Fr对带轮半径的关系，在线性滑动极限（●）和接近峰值效率极限（■），对于毛边带的理论值（阴线区）与实验比较Fig.7 The measured dependence on pulley radius of Ft/Frat the linear slip limit（●）and the near－peak efficiency limit（■）for the raw－edged belts compared with theories（hatched regions）

表1 测量和计算V－带数据Table1 Measured and calculated V－belt data

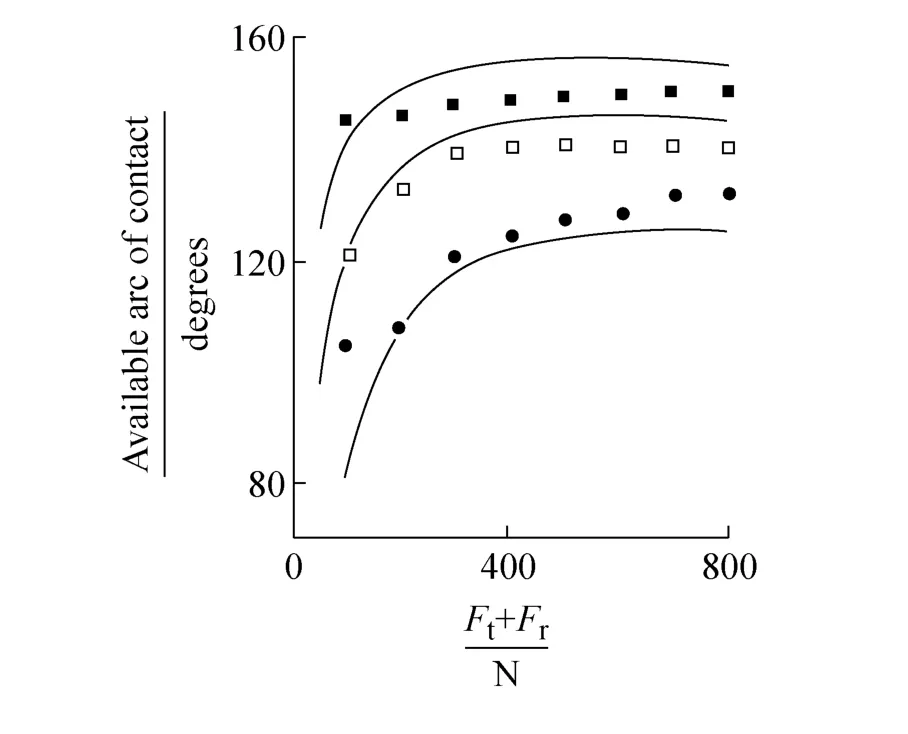
图8 在缺乏转矩传递有效接触弧和总带拉力间关系，毛边带在带轮半径51mm（■），36mm（□）和21mm（●），与理论比较（实线）Fig.8 The dependence of available arc of contact on total belt tension in the absence of torque transmission for rawedged belts at pulley radii of 51mm（■），36mm（□）and 21mm（●），compared with theory（solid lines）

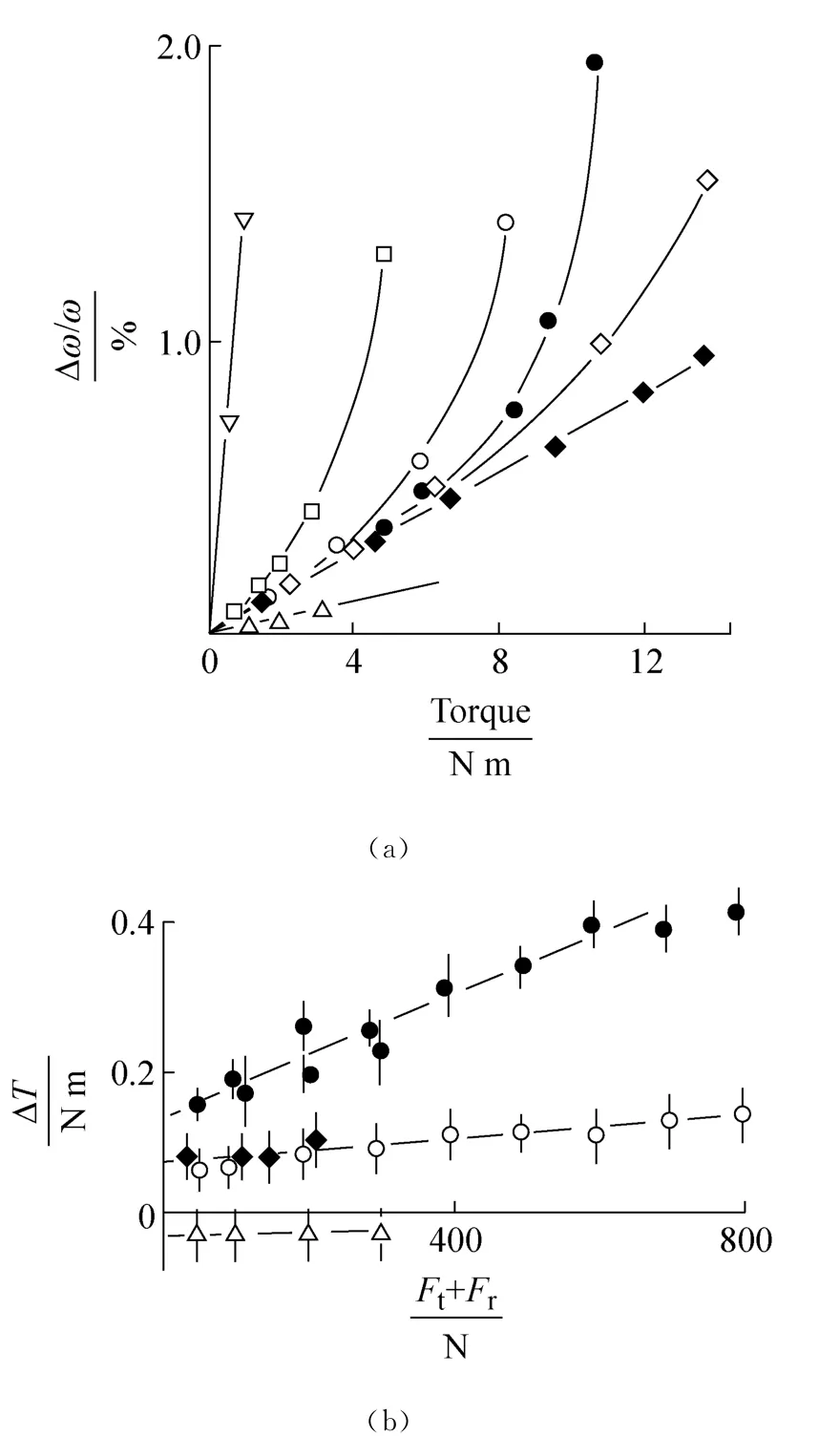
图9 对50mm半径带轮（a）矩形截面带在平带轮上Δω/ω对转矩的关系总带拉力100N（□），200N（○）和400N（◇），对于毛边带在槽带轮在200N（●）和400N（◆）和对于帘布（△）和带体（▽）部分矩形带和（b）ΔT和Ft＋Fr关系对于矩形截面带（●），帘布（○）和带体（◆）部分带和尼龙带（△）Fig.9 The dependence，for 50mm radius pulleys，of（a）Δω/ωon torque for rectangular section belts on flat pulleys at total belt tensions of 100N（□），200N（○）and 400 N（◇），for raw－edged belts on grooved pulleys at 200 N（●），and 400N（◆）and for the cord（△）and carcass（▽）parts of the rectangular belt and（b）ΔT on Ft＋Frfor rectangular section belts（●），cord（○）and carcass（◆）parts of belts and a nylon band（△）

图9b示转矩损失随带总拉力变化。全带的转矩损失随拉力以较大的比率增加为4×10－4Nm/N，V型带图6b示为3×10－4Nm/N。仅帘布或仅带体的转矩损失与拉力无关，如同拉成的尼龙带。对于尼龙带记录值为－0.03，由转矩损失测量得出，确信其限制于零数据之内。

值得注意的仅帘布或仅带体的阻滞损失几乎等于0.08±0.04Nm，它强调在发生损失时帘布截面的重要性。同时它还注意与0.08值比较，齿形带在51mm半径带轮上的阻滞损失为0.04±0.03 Nm，或者说齿形带的损失被其帘布所支配。

数值资料列于表2，带的变形数据下节研究。

表2 测量和计算平带的数据Table2 Measured and calculated flat belt data，R＝55mm

5.6 带变形特征

表1列出了V型带变形特性的测量额定值和范围以及k1和k0的计算值。对于缠绕和齿带对于c无范围引用，仅对其中一带进行这些情况试验，除了缠绕带外，发现g可认为与带轮半径无关。对于带轮半径大于36mm的g180和g90值列于表内，对于21mm半径的g180等于0.04mm2/N，而g90没有测量。

测量的μ值变化最大，带采用固定支承，在滑动试验中，对于毛边带例如μ变化从0.3至0.65。在主要试验程序中，根据测量传递最大转矩推断μ＝0.48，但在最大转矩Fr降到的低值，造成接触弧减小应处于允许情况。在采用和毛边V型带相同材料制成的矩形平带试验中，按最大转矩试验得出μ＝0.56。对于μ的不确定性，对于k1误差和k0严重误差，大体上是可靠的。

采用测量V型带g180同样方法，还研究了矩形带在平带轮上的径向屈服。找到带顶面径向向带轮移动与带的拉力成比例，得出g等于0.012mm2/N，在表2已采用该值写出g/R2。根据速度损失试验，假定（Δω/ω）（Ft－Fr）等于1/c，推断出表2中的c值，对V型带用同样方法求出EI。发现垂直于纤维加强筋方向在25MPa带体的杨氏模量G＝8 MPa（在沿纤维方向测出的杨氏模量为65MPa）。

6 讨论

已经对AV10V型带传递功率损失作详细地试验研究。如图4所示效率随带轮半径和带拉力变化的监测情况，一般采用给定的可达到的效率数据。例如效率随减小半径而降低，齿形带效率大于毛边带，这种现象在低拉力比高拉力更加突出。然而本文的主要目的是研究功率损失的原因。

6.1 滑动转矩损失

本文大部分内容是转矩损失。本试验（图5b和6b）与其他作者（1，11）一致，它已表明转矩损失与传递转矩无关，它随带总拉力成比例增大。图6b描绘了该结果，同样图10表明转矩损失随带拉力的损失比率，同时还表示与带轮半径成反比。

一种已有的转矩损失理论［式（9）和图3b］预期转矩与带拉力成比例，但在试验中提出几乎与带轮半径无关。这里研究了一新的但接近分析［式（22）和图3b］预测转矩损失与带轮半径成反比，但随带拉力非线性增大。然而这两种理论都低估了拉力对转矩损失的影响，这点比较图3b和6b可以看到。

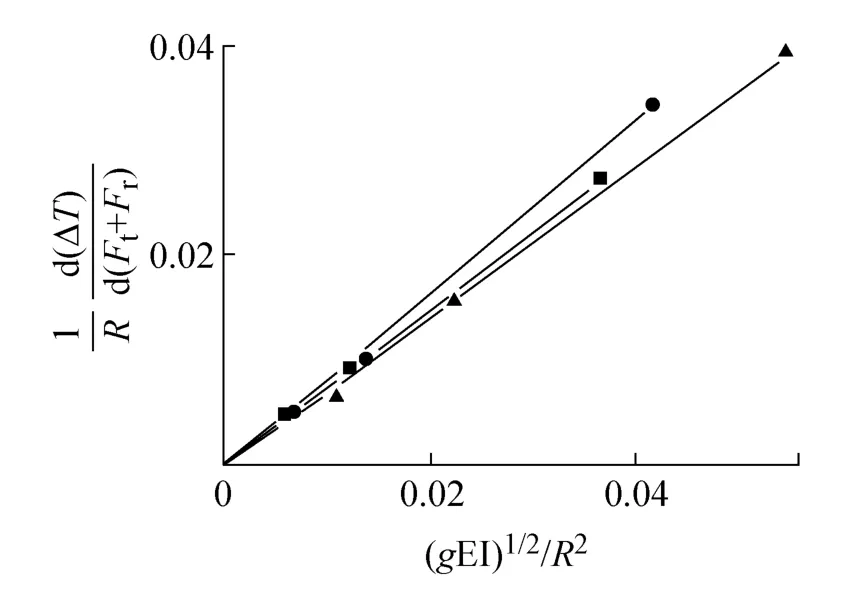
图10 ΔT/｛（Ft＋Fr）R｝与（gEI/R4）1/2间关系，对于毛边（●），缠绕（▲）和齿带（■）Fig.10 The dependence ofΔT/｛（Ft＋Fr）R｝on （gEI/R4）1/2 for raw－edged（●），wrapped（▲）and cogged（■）belts

实验结果比理论预测更简单，式（22）表明ΔT/｛（Ft＋Fr）R｝与（gEI/R4）1/2和｛g/（EI）1/2｝F有关，图10示事实上仅与（gEI/R4）1/2有关，适当观察的一经验公式为

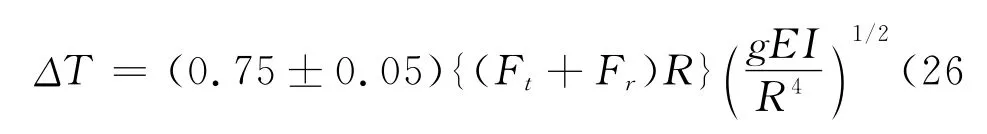
该理论的改进没有进展，式（11）示按带轮入口和出口转矩差计算转矩损失。数值计算表明，这些转矩更大于它们的差值。两者作小的改变，对转矩损失将产生大的影响。分析的一个明显缺点，它采取出口处边界条件在φ＝φB特性和在入口区φA相同。此外，研究提出的由滑动模拟导出的式（8）这样高的摩擦系数是真实的。就有关第一点而论，后面更精确的分析式（9）已不再比一个近似的成功，它有一更主要的原因是对于理论上的缺点。

在这方面，观察式（9）平带明显承受几乎和相同截面V型带的转矩损失，没有可能对于平带结果解释带进入或离开槽的滑动，根据圆周和轴向剪切带体在入口和出口出现不同的变形导致转矩损失，用一圆柱作为安置一不可压缩的弹性带的弯入的刚性基础，大家知道，要求的平面截面在带内是不保持平面的（15）。

本文作者们相信，在小半径带轮上转矩损失的进一步分析，必须考虑带截面在进口和出口处的歪斜。观察（图10）转矩损失和（gEI/R4）1/2的关系与此是一致的。g的模拟（8）推荐和E成反比，和B/H 在I与 BH3成正比时成正比，因此，（gEI/R4）1/2与（H/R）2（B/H）成正比。在一些进一步的研究中，可以出现歪斜，带体圆周应变（H/R）和带尺寸比（B/H）之间的联系。

6.2 阻滞转矩损失

为其他的原因，也注意到平带的试验。试验中帘布和带体分开，如带采用分离（图9b）每一部分等于全带的弯曲阻滞转矩损失，这表明了帘布区在弯曲阻滞损失中的重要性。

在采用V型带试验中，该阻滞转矩损失随带轮半径减小而增大，该增加值并不表示与半径成反比，该转矩接近于描述设备不可靠性结论的转变的极限。

齿形带的弯曲阻滞损失，显然小于其他带。这说明齿形带在低带拉力下在小半径带轮上具有较大的效率。该较低的弯曲刚度增加带径向屈服的消耗，可靠地达到较小的弯曲的阻滞。因而有利于降低刚度，不能保持减小滑动转矩损失。在大的带拉力下，滑动损失变弱，失去齿带弯曲损失的优势。

6.3 低转矩下速度损失

已经研究了速度损失和传递转矩的线性关系。图6a示在高带拉力下，（Δω/ω）/（Ft－Fr）与带拉力无关，并且除毛边带外很接近由式（1）预期的数值。还不知道什么原因毛边带在这方面不同于其他带。

随着带拉力降低，速度损失在小半径带轮上比大半径带轮上增加更快。图11a证实了毛边带速度损失增加正和带拉力相反，该增加比率同样近似和R2成反比，这点和其他带相同。式（27）是对于所有三种V型带经验和监测一致，仅对毛边带有误差，因为已经提及，在高拉力下，它与式（1）有偏差。

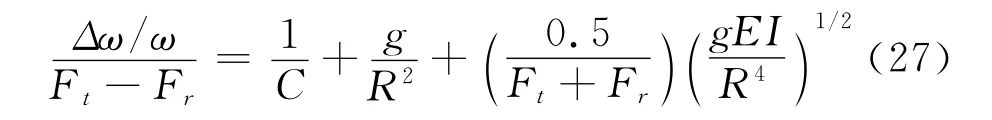
已经开发了一个稳定的理论模型表明式（27）的形式，然而反复适当作平带试验。已知带体的剪切可导致速度损失和1/R2成比例。如式（2）所示。已导出在平带试验中剪切速度损失的重要性见表2，最后一列给出因剪切与假定的接触弧有关的（Δω/ω）/（Ft－Fr）的两种估算。对α＝π，名义接触弧，该剪切速度损失项大于径向屈服项（g/R2）两倍，但小于伸长项（1/C），对于仅帘布带假定相同。剪切径向屈服和伸长的总和为2.9×10－5/N明显小于测量值4.0×10－5/N。但如果接触弧实际设想为2.6弧度，那么理论与实测值的差异仅10%。虽然它们未经实测，在本试验中，15°的入口和出口区是合理的。

式（2）不能直接用于V型带，但它可用来引导帘布剪切与其特性的关系，对于V型带必须确定合理的A和α值。G和C已分别给出其测量值为8 MPa和7500N，d/t任意假定为1，A等于0.01。已进一步假定有效弧长，对于剪切是总弧长，小于进口和出口弧长。对于α已采用按图8作其理论估算。图11b示毛边带用式（1）预算的速度损失超过依据式（2）预测值。破折线表示超出值和式（2）间相等，并看到对结果的包络线。包络线上的结果是根据低总拉力试验得出的，与包络线分开是发生在高总拉力。根据带体剪切可能出现速度损失和总带拉力及R2相反的关系，接触弧随带拉力降低而减小，但它不能用模拟的平带特性来模拟。

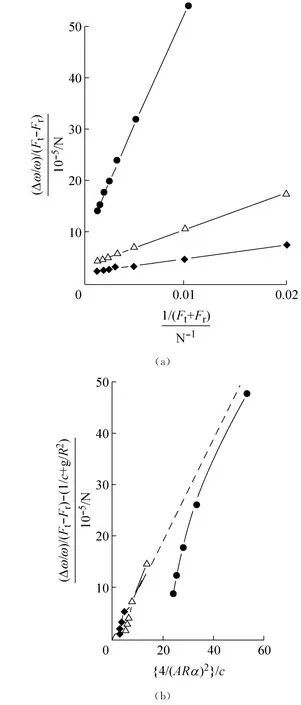
图11 线性速度损失关系对于AV10毛边带在51mm半径带轮上（●），36mm（△）和21mm（◆）表示（a）相反拉力影响和（b）可能带体剪切的影响Fig.11 Linear speed loss dependences for the AV10raw－edged belts on pulleys of 51mm（●），36mm（△）and 21 mm（◆）radius，showing （a）inerse tension effects and（b）possible carcass shear effects

6.4 过渡打滑

在式（26）和（27）中可以看到带轮半径对转矩和速度损失的大的影响，带轮半径还强烈地影响了最大的拉力比，使其支承绕于带轮而没有过度的功率损失，如图7所示。当R＝51mm时，依据不只是弱非线性预测，当R＝21mm，几乎到非线极限，该许可拉力比下降。这已不再企图在本研究中，采用在非线性区内预测速度损失的变化，然而值得指出的是，对R＝21mm，测得的Ft/Fr的极限值等于5，这和用绞盘公式［式（36）］对平带采用μ＝0.5与π弧度接触弧预测的值4.8的差别并不太显著。该预期楔入带轮槽有效摩擦力增大值，已被带径向运动造成的降低完全补偿。

设计中一般推荐（16，17），对于名义接触弧为π弧度，Ft/Fr值，不论带轮半径多少应不超过5。图5示就有关效率而言，对于大带轮半径是极稳定的。

最后，简要说明扩充的讨论，考虑毛边带的传递功率大小与典型的中等汽车交流电机要求功率的匹配。图12示对于一现代中等尺寸（55A）全输出交流电机（按私用交通工具Lucas CAV有限公司1986）要求的典型输入功率。它还表示该功率可以用AV10毛边带传递，没有过度的功率损失，假定带包角为180°，Ft＋Fr＝500N，交流电机带轮半径为30mm，取Ft/Fr＝7（图7）。假定两带轮以固定中心距驱动（按与本试验对比），对于带的测量质量0.083kg/m在高速轴按离心力影响计算传动的损失。交流电机带轮上带包角实际小于180°，对于一交流电机，已估算第二带的传动特性，对于120°的包角，带和交流电机有很好匹配特性。设想该两要点是包角和在速度低于2000r/m可传递的功率，这是交流电机不能采用的。