木荷次生林经营密度调控技术的研究

刘发林，曾思齐，吕 勇，刘勉声，肖化顺，彭其龙，刘 玉

(中南林业科技大学，湖南 长沙 410004)

木荷次生林经营密度调控技术的研究

刘发林，曾思齐，吕 勇，刘勉声，肖化顺，彭其龙，刘 玉

(中南林业科技大学，湖南 长沙 410004)

为了提高次生林的经营水平，提出了竞争结构单元的新概念，以地上部分生物量为因变量，郁闭度为自变量，模拟木荷次生林地上部分生物量与郁闭度间关系。结果表明：林分地上部分生物量达最大时，林分的郁闭度为0.685 4；若控制郁闭度为0.68，竞争结构单元面积越大，竞争结构单元越少；竞争结构单元面积最大时，单位面积林分最少保留株数等于最少竞争结构单元个数与每个竞争结构单元林木株数（5株）的积。以木荷标准地资料为例计算了木荷次生林抚育间伐强度，表明基于竞争结构单元的抚育间伐技术可在次生林经营中推广。

木荷次生林；经营密度调控；抚育强度；竞争结构单元

林分密度调控是森林生态系统经营的关键技术之一。通过适时适度调整林分密度，可改善林木干形，促进林木直径、材积生长和生物量积累[1]。大量试验研究表明，密度对林分生长有一定的制约作用，即林分密度效应，研究学者先后构建了平均胸高直径、平均胸高断面积、平均单株材积、单位面积蓄积等个体或群体的大小间关系模型，如密度效应抛物线模型、密度效应倒数模型、密度效应乘幂模型、直径（断面积）密度效应倒数模型等[2-6]，这些模型指导森林经营密度调控。如程煜等[7]曾经应用密度效应模型拟合了马尾松人工林的密度效应和蓄积收获模型。江希钿等[8]利用单纯形法模拟柳杉密度效应新模型，经验证模型能较好地模拟柳杉人工林密度效应，且优于二次效应模型和密度效应倒数式模型。叶秀妹等[9]利用回归分析模型模拟了天然黄山松林分密度效应，证明了Conb-Douglas函数可用来研究不同立地及不同发育阶段的林分密度效应。叶绍明等[10]利用不同密度尾叶桉林分标准地资料，把优势高作为变量因子引入密度效应，建立了抛物线式模型，模型可以反映不同立地和不同发育阶段的密度效应，通过模型可以求解不同立地尾叶桉林分最适宜密度。王洪英等[11]利用生物量密度效应模型对黄土高原木荷人工林密度效应进行过探讨研究。综上分析，前人对林分密度效应的研究主要集中于人工林，然而对次生林密度效应的研究相对较少。本研究以炎陵县青石冈国有林场木荷次生林为研究对象，根据林分竞争结构单元分析、模拟地上部分生物量与郁闭度的关系，控制林分郁闭度，通过密度调控使次生林生态系统维持在理想的结构状态，对森林可持续经营具有重要的理论价值和实践推广意义。

1 试验区概况

试验区设在炎陵县青石冈国有林场，位于东经 113°34′45" ～ 114°07′15″、 北 纬 26°03′03" ～26°38′30"之间。林场属于中亚热带季风湿润气候区，中山地貌，成土母质母岩以花岗岩为主，海拔800～1 200 m，为黄棕壤。全场现有林地面积28 026.2 hm2，活立木蓄积约1 578 806 m3，其中阔叶林面积为8 595 hm2，蓄积为650 823 m3，森林覆盖率95.26%，木荷Schima superba、枫香Liquidambar formosana、青冈栎Cyclobalanopsis glauca等为群落主要组成树种，主要分布在海拔1 600 m以下。森林植被类型可分为9个植被型22个群系（丛），维管束植物共有2 019种，其中资源冷杉Abies ziyuanensis、银杏Gingo Biloba、南方红豆杉Taxus chinensis、南方铁杉Tsuga dumosa等均在本区呈大面积野生分布。

2 研究方法

2011年3～11月，在研究区选择不同密度的木荷次生林，设置形状与大小为20 m×20 m的标准地35块；采用标准地调查方法对试验林进行调查，在标准地内进行每木调查。将标准地的每木调查结果按等径级分为3～5级，各径级选取1～3株平均木，共计75株样木，伐倒平均木进行生物量调查。采用全称重法测定林木树干生物量、标准枝法测定枝叶生物量。

3 结果与分析

3.1 木荷地上部分生物量与郁闭度之间的关系

根据木荷林分标准地及标准木调查数据，对总生物量与郁闭度之间的相关关系进行拟合，建立总生物量（W总）与郁闭度（P）之间的回归方程，即W总= -18.453 1+101.807 8P-74.268 9P2，r =0.854。木荷次生林地上部分生物量与郁闭度之间呈抛物线关系。根据林分平均胸径与林分密度的相关关系可知，随着林分密度的增大，林分单木胸径变小，林分郁闭迅速，林木枝生长受阻，因此需要对林分采取适度抚育间伐，保证林分适宜的生长空间，实现经营目标。通过求导可以得出：郁闭度等于0.685 4时，林分地上部分生物量W总达最大。但是，随着林分平均胸径和树高的生长，导致林分郁闭度增加，因此，要使木荷次生林林分生物量达到最大，在经营过程中控制木荷次生林林分的郁闭度保持在0.685 4。

3.2 基于竞争结构单元的木荷次生林最少保留密度

竞争结构单元定义为以对象木为中心，其4个象限内各选一株与对象木最邻近的林木作为竞争木，对象木与4株竞争木组成结构单元。对象木4个象限内最邻近的4株竞争木围成的平面四边形的面积称为竞争结构单元面积（见图1）。

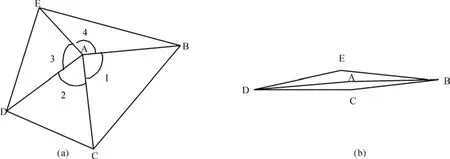
图1 竞争结构单元Fig.1 Competitive structural units

如图1（a）所示，A为对象木，B、C、D、E分别为对象木各象限内最邻近竞争木，∠1、∠2、∠3、∠4分别代表∠BAC、∠CAD、∠DAE、∠EAB。AB、AC、AD、AE分别为对象木与4株竞争木的水平距离。因为竞争结构单元构成平面四边形，而对象木与4株竞争木的距离联线把竞争结构单元分成4个任意三角形。所示平面图1中，竞争结构单元中已知对象木与4株竞争木的距离，令：|AB|=d1、|AC|=d2、|AD|=d3、|AE|=d4，那么当且仅当时，(SBCDE)max成立。所以，当E、A、C 3株林木共线和B、A、D 3株林木共线且相互垂直时，竞争结构单元面积最大。如图1（b）所示，如果竞争木C和E再无限靠近对象木A，最终结果为A、C、E同株，此时与竞争结构单元的定义不符了，就要重新选择邻近木作为竞争木。因此，平面四边形面积有最大值，其面积有下界但没有最小值。

竞争结构单元面积最大时，单位面积（hm2）上的竞争结构单元的个数最少，而每个竞争结构单元林木的容纳量为5株，则单位面积林分最少保留株数等于最少竞争结构单元个数与每个竞争结构单元林木的株数（5株）的积。

假设对象木与竞争木的平均冠幅半径为R，L为对象木与其相邻4株竞争木距离的平均值。根据林分郁闭度的定义可知：P=2R/L，若控制以生物量最大为经营目标的木荷次生林的郁闭度为0.68，根据郁闭度的定义，则平均冠幅半径R和对象木与其相邻4株竞争木距离的平均值L有以下关系。由0.68=2R/L可知，L=R/0.34。竞争结构单元面积最大值与竞争结构单元平均冠半径的函数：(SBCDE)max=2L2=2(R/0.34)2=17.301R2。根据此函数可得不同竞争结构单元平均冠半径对应的林分密度，即林分最少保留密度见表1。

因此，根据现实林分的竞争结构单元的平均冠半径，查表1得知林分的最少保留株数，因而估算抚育间伐的最大强度。

3.3 木荷次生林现实林分抚育强度

随机抽取研究区木荷标准地调查数据，统计林分内现实林木株数（简称为N现实），求得木荷次生林平均冠半径，通过查定木荷次生林最少保留密度表，可得标准地所在林分最少保留密度（简称为N最少）。根据生物量最大的最少保留密度的内涵，可知：

若N最少＞N现实，说明现实林分密度低于最少保留密度，需要在林内补植林木，最少补植数量为N最少与N现实之差。

表1 木荷林分最少保留密度Table1 Least reserved density of Schima superba stand

若N最少＜N现实，说明现实林分密度偏大，林木比较拥挤，进行抚育间伐，最大间伐数量为N现实与N最少之差。

以19号标准地为例计算木荷次生林林分抚育间伐强度。形状和大小为20 m×20 m的19号标准地内共计94株林木。根据19号标准地每木检尺数据，统计林分平均冠半径为1.2 m，查表1得知，单位面积林分内最少保留株数为2 010 株/hm2，则该样地上最少保留密度约为81株，即N最少＜N现实，因此，最大间伐株数=N现实-N最少=94-81=13，最大株数抚育强度为13.8%。

4 结论与讨论

人工纯林的抚育间伐强度研究相对成熟，一般根据林分测树因子（胸径、树高、胸高断面积、蓄积等）生长规律确定抚育方案，而对于次生林的抚育强度研究鲜见报道。通过拟合木荷次生林林分地上部分生物量与郁闭度的关系模型，提出竞争结构单元面积，建立最大竞争结构单元面积与竞争结构单元平均冠半径的函数，得到不同竞争结构单元平均冠半径对应的林分密度，即林分最少保留密度表，为次生林抚育间伐提供理论参考。

运用林分最少保留密度表能够获得在不同竞争格局、林分密度、林木大小下的抚育强度。经标准地林分试验证明，计算林分中竞争结构单元的平均冠半径，再查定对应林分的最少保留密度表，根据现实林分的密度与最少保留密度之间的关系，确定次生林是否需要进行抚育，如需抚育则确定最大抚育强度。抚育方案合理，能够较好地满足对林分实施抚育间伐的预期要求，克服了凭经验制定抚育间伐强度的方案。

基于竞争结构单元的最大抚育强度计算方法简单，操作方便，不需要砍伐解析木，浪费森林资源。另一方面如果因林木冠幅信息采集不方便和精度不高，可以通过林木冠幅与胸径的相关关系，把表1转换为竞争结构单元平均胸径与最少保留株数的相关表。

[1] 孟宪宇.测树学[M].北京:中国林业出版社,1996:122-124.

[2] 刘景芳.编制林分密度管理图研究报告[J].林业科学,1980,16(4):241-251.

[3] 肖兴翠,李志辉,唐作钧,等.林分密度对湿地松生物量及生产力的影响[J].中南林业科技大学学报,2011,31(3):123-129.

[4] 陈 辉,何宋明,洪 伟,等.林木人工林密度效应模型研究[J].福建林学院学报,1992,12(3):277-282.

[5] Drew T J, Flewelling J W. Some recent Japanese theories of yield density relationships and their application to Montery pine plantations [J]. Forestry Sector,1977,23(4):517-534.

[6] 张大勇,赵松林.森林自疏过程中密度变化规律的研究[J].林业科学,1985,21(4):369-374.

[7] 程 煜,洪 伟,吴承祯,等.闽北马尾松人工林密度效应蓄积量改进模型[J].河南农业大学学报,2003,36(2):147-150.

[8] 江希钿,黄烺增,江传阳,等.柳杉人工林密度效应新模型[J].福建林学院学报,2005,25(3):193-196.

[9] 叶秀妹,刘 钦,龚龙振. 天然黄山松林密度效应规律[J].福建农林大学学报：自然科学版,2009,33(3):352-354.

[10] 叶绍明,杨 梅,黄宝灵,等. 基于密度效应模型尾叶桉人工林最优株数密度的研究[C].第九届中国林业青年学术年会论文摘要集,2009:144.

[11] 王洪英.黄土高原人工刺槐林土壤水分动态及生物量的密度效应研究[D].北京:北京林业大学,2006:47-50.

Study on density control technology of Schima superba secondary forest

LIU Fa-lin, ZENG Si-qi, LU Yong, LIU Mian-sheng, XIAO Hua-shun, PENG Qi-long, LIU Yu

(Central South University of Forestry & Technology, Changsha 410004, Hunan, China)

∶ In order to improve the management level and provide management basis of secondary forests, a new concept of competitive structural unit was put forward. Aboveground biomass was taken as the dependent variable, canopy density was taken as the independent variable, the relationship between aboveground biomass and canopy density of Schima superba secondary forest was simulated. The results show as followings: the biomass reached the maximum value when canopy density was 0.685 4; if the canopy density was controlled at 0.68, the area of competitive structural unit was more larger, the number of competitive structural unit was less, each competitive structural unit had five trees. When the competitive structural unit area reached the maximum value, the least reserved density equaled to the number of competitive structural unit multiplied by five. Sample plot had been taken as an example to calculate thinning intensity of Schima superba secondary forest. It showed that thinning technology which based on competitive structural unit can be extended in secondary forest management.

∶ Schima superb secondary forest; density regulation; thinning intensity; competitive structural unit

S711；S753.7

A

1673-923X(2013)11-0026-03

2013-04-24

国家林业局林业公益性行业项目“南方集体林区次生林抚育间伐与高效利用技术研究”(201004032)；湖南省教育厅项目：“木荷天然次生林竞争生长规律研究”（13C1155）

刘发林（1975-），男，湖南株洲人，讲师，博士，从事森林经理教学与科研工作；E-mail：liufl680@126.com

[本文编校：谢荣秀]