牺牲空间算法求解平板车装货问题

庞小琪

(成都工业学院 教务处，成都 610031)

“2辆铁路平板车的装货问题”是福特汽车公司一个具体问题的修正与简化，由佐治亚理工学院的J·Bartholdi［1］提供并作为1988年的美国大学生数学建模竞赛题目。该题是解决7种规格的包装箱要装到2辆铁路平板车上去的问题。以前对于此问题的讨论，大多是应用数学分析方法，根据数据的一些特殊情况简化后再进行计算。但分析过程比较复杂，且装载货物的情况比较特殊，而牺牲空间算法可以不用复杂的分析过程，一般情况下都能简单而迅速地求解。

1 问题分析

“2辆铁路平板车的装货问题”即在包装箱的宽和高相同，但重量和厚度不同，且每种包装箱的厚度、重量以及数量为已知的前提下，把7种规格的包装箱(Ci表示第i种规格，具体见表1)装到2辆平板车上去并使所占的空间最小。如图1所示，每辆平板车有L m长的地方可用来装包装箱，载重为T t。由于当地货运的限制，对C5、C6、C7类的包装箱的总的长度不能超过M cm。

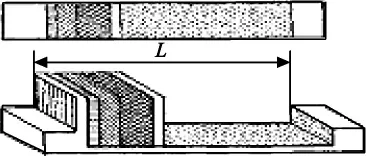
图1 平板车装货示意图

表1 7种货物的数量及规格

根据题目分析:7种包装箱不可能全部装到这2辆平板车上去，究竟怎样把这些包装箱分配在2辆平板车上，才能使浪费的空间最少?因此需考虑象面包片那样装载，问题就可以转化为怎样装载才能使剩余空间最小。从表面上看，该问题是以装载在2辆平板车上各种包装箱的数量为决策变量，以装载总厚度最大为目标的一个整数规划问题。如果按照优化模型的求解过程只能得到1组解，但实际上由于包装箱堆放的位置不确定，如果只有1组解，很难作为实际装载方案的参考，必须根据实际情况选择不同的装载方案以使剩余空间最小，所以需要找出多种装载方案。

2 算法分析

2.1 穷举法

穷举法简单易用、操作简单，但是对于时间复杂度过大的情况则无法进行计算。本文所涉及的是将7种货物装载到2辆平板车上去的问题，由此分析可知，应有14个变量即拥有14重的循环。

以C1为例，该种货物在2辆平板车的装载数量为0～8，则14重循环的时间复杂度为(9×8×10×7×7×5×6)2=1.120 2e+012，这显然是计算机无法承受的。又由题目条件对C5、C6、C7类的包装箱的总长度不能超过M cm来进一步分析，可以发现，C1、C2、C3、C4这4种货物必须全部装完，从而就剩下10重循环，时间复杂度为9×8×10×7×(7×5×6)2=1.270 08e+09，虽然计算机勉强能够运行，但计算速度缓慢。

2.2 启发式算法

当穷举法失效时，很容易想到启发式算法。启发式算法的优点是迭代次数少、计算迅速［2］，但是该算法寻找的是近似解，不一定能够找出最优解，更不能找出全部的最优解。所以对于该问题，要想找出所有平板车装载的最优方案是不可能的。

2.3 牺牲空间算法

算法复杂度分为时间复杂度和空间复杂度。时间复杂度是指度量算法执行的时间长短;而空间复杂度是指度量算法所需存储空间的大小。牺牲空间算法是以牺牲存储空间为代价，换取较短的算法执行时间［3］。

空间复杂度算法表示在计算机存储器上所占用的存储空间［3］，包括存储算法本身所占用的存储空间，算法的输入输出数据所占用的存储空间和算法在运行过程中临时占用的存储空间3个方面。虽然该算法对于时间复杂度较大的情况下可以考虑，但是也应该考虑到如果占用的存储空间过大，会出现“Out of memory(内存超过限制)”的错误。对于一个算法，其时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时，可能会使空间复杂度的性能变差，即可能导致占用较多的存储空间;反之，当追求一个较好的空间复杂度时，可能会使时间复杂度的性能变差，即可能导致占用较长的运行时间。［5］然而，恰当地牺牲有限的存储空间来减少时间复杂度，从而实现对问题的求解是可行的。

为了减少时间复杂度，可以通过牺牲一定的存储空间来存放满足条件的装载方案，再从中寻找最优的存储方案。对于该问题，一辆平板车就只有7个变量即7重循环。7重循环的总循环次数只有1 058 400，计算机完全能够承受。但是如果把所有满足条件的放置在平板车的方案存储下来，所需存储空间是非常巨大的。因为要找的是使得剩余空间最小的最优解，所以对于装载货物很少的方案可以不用考虑，即限定满足条件方案的总长度在(L－ε，L)之间，其中L是一辆平板车的长度，ε为预计的剩余空间。ε取得太小，就找不到最优解;ε取得太大会使存储空间较大。这里不妨取ε=1，如果能找到最优解则不用再调整了，如果不能找到最优解可适当增加ε的值，直到找到最优解为止。

然后，把已存储的方案一一取出进行组合，判断是否满足货物数量、重量，并进行比较找出剩余空间最少的所有方案。

3 算法实现

对于该问题L=10.20 m，ε=1，ti为第i种货物的厚度，wi为第i种货物的质量，总质量限制为40 t，则算法的具体实现为:

1)找出并存储满足条件的装载方案

设1辆平板车装载第i种货物的数量为xi(i=1，2，…，7)，通过7重循环找出满足条件的装载方案:

①生成候选装载方案

第1重循环x1从0到8取值，第2重循环x2从0到7取值，…，第7重循环x7从0到8取值，则装载方案为［x1，x2，x3，x4，x5，x6，x7］;

②存储满足条件的方案

从而，可找出852种满足条件的装载方案，运行时间不到1 min。

2)把存储的方案进行两两组合，使得各种货物量不超过限制且剩余空间最小

通过步骤1)存储的方案是满足装载方案的，因为是2辆平板车的装货问题，而存储的装载方案是在1辆车的装载方案，则将存储的装载方案进行两两组合，并判断各种货物数量不超过限制且剩余空间最小这2个条件。即从852种方案每次取2种方案，运算次数为C2852=362 526，判断各种货物数量不超过限制且剩余空间最小这2个条件，从而可以很快地找出满足条件的装载方案。

设装载方案Xi(i=1，2，…，852)，M为每一种货物的数量上限，通过2重循环找出满足条件的装载方案，实现过程如图3所示。

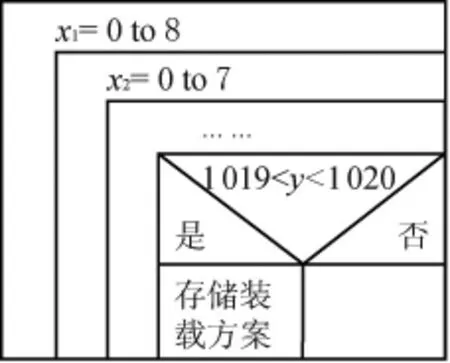
图2 寻找满足1辆车装载方案的N-S图

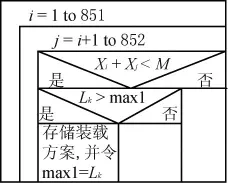
图3 寻找满足2辆车装载方案的N-S图

最后计算出最优的装载方案有60种，最小剩余空间0.6 cm，总运算次数1 058 400+362 526=1 420 926。

4 结语

通过牺牲空间算法大大提高了程序的运行时间，并且能够把所有满足条件的装载方案都找出来，不会出现漏解。因为在存储方案的选择时去掉的只有不满足条件或者达不到最优解的方案，从而对该问题进行了比较完美的求解。牺牲空间算法不仅对于该问题适用，对于组合、优化等类似问题同样适用。

［1］BARTHOIDI J.The outstanding railroad flatcar papers［J］.The UMAP Journal，1988，9(4):399 －103.

［2］MOTWANI R，RAGHAVAN P.Randomized algorithms［M］.New York:Cambridge University Press，1995.

［3］APPLEBAUM B，SHAIY I，KUSHILEVITZ E.Cryptography in NC0［J］.S IAM Journal of Computing，2006，36(4):845 －888.

［4］石竑松，秦志光.保持空间复杂性的算法组合［J］.计算机应用研究，2010(6):2020－2023.

［5］算法的时间复杂度和空间复杂度［EB/OL］.［2012－12－01］.http://wenku.baidu.com/view/19634f5f804d2b160b4ec049.html