基于物理意义的二维散点图类型划分与遥感蚀变信息提取

张远飞，袁继明，杨自安，吕伟艳，张思颖，4

(1．有色金属矿产地质调查中心，北京 100012;2．桂林矿产地质研究院，桂林 541004;3．北京吉利大学，北京 102202;4．中南大学，长沙 408309)

0 引言

遥感多(高)光谱数据是一种多元数据集合，每个像元代表一个波谱矢量。图像中所有像元点构成了高维光谱空间中的点阵，这个空间点阵具有一定的几何结构。但是，高维空间的点阵几何体形态是无法直接观测的，只有从低维空间入手，通过分析二维(2个波段)和三维(3个波段)数据的散点图来探讨高维情况下光谱数据点阵的几何结构及其在空间中的聚类分布特征。本文主要基于二维散点图的几何结构特征来探讨一些与遥感蚀变信息提取有关的问题。

笔者把遥感图像中2个低相关且在其生成的二维散点图上能使某类(或某些)蚀变矿物偏离背景的波段组合称之为波段序偶［1］。例如，某类蚀变矿物的1个反射峰波段与1个吸收谷波段组合就属于波段序偶。事实上，各种不同的技术方法在提取遥感蚀变矿物信息时，都需要寻找相应的波段序偶。遥感图像二维散点图正是表达波段序偶光谱空间结构信息的最佳图示方式。因此，需要进一步研究各种二维散点图的空间结构特征及其所包含的丰富信息。

本文所讨论的问题是在“遥感蚀变信息多层次分离技术”模型框架［2］下的光谱空间结构分析技术内容的一部分。笔者曾在文献［3－4］中较为详细地讨论了遥感蚀变信息提取中有关光谱数据点阵空间(重点是剖析二维散点图)的几何结构问题，主要分析了光谱数据点阵空间的背景－异常子空间模型，遥感图像二维散点图的分布规律、形态规则、多层次聚类套叠等基本空间几何结构特征，基于2个波段概率密度联合高斯分布模型估计二维散点图的椭圆几何参数，以及遥感图像背景、干扰和蚀变异常与二维散点图空间结构的关系等。本文是上述研究的延续，从物理意义的角度进一步讨论二维散点图类型的划分问题，并结合实例分析阐述不同类型的散点图在遥感蚀变信息提取中的作用与指导遥感蚀变信息提取方法选择的重要意义。

1 二维散点图基本特性与意义

图1是由某个地区TM图像的第5，7波段数据所生成的二维散点图。

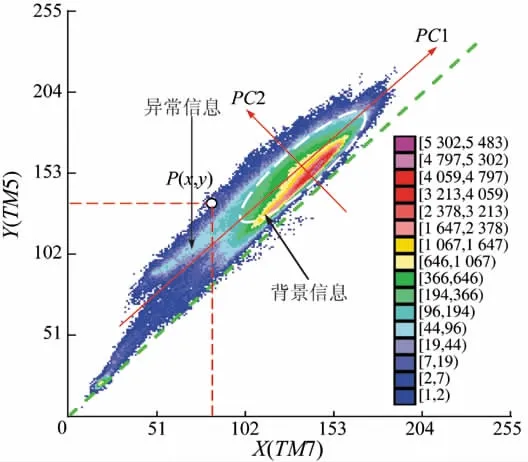
图1 遥感图像的二维散点图Fig．1 2D scatter plot of remote sensing image

参看图1，本文根据蚀变矿物的光谱特征对二维散点图做几点约定:①要求X，Y轴的坐标单位统一;②把选定的某类蚀变矿物的反射峰波段作为Y轴、吸收谷波段作为X轴(如对于TM图像，研究羟基蚀变矿物时，应选TM5作为Y轴，TM7作为X轴)。二维散点图所包含的信息如下:

1)二维散点图［5］反映了二维变量数据空间的聚类结构。图1中白色虚线椭圆边界内的集群点为背景信息，边界外部的点群为异常信息(包括干扰信息与蚀变信息)，故称这里的椭圆为“背景”椭圆。更多的相关描述可参考文献［4，6－8］。

2)二维散点图也是2个变量主成分分析的几何解释，其中PC1为第一主成分轴，PC2为第二主成分轴。对于多波段(3波段以上)主成分分析(比如Crosta定向主成分分析)，可以通过对多个二维散点图的观测去重构思维中的高维光谱数据点阵几何结构。

3)在约定X轴表示具有吸收谷波段(如TM1或TM7)，而Y轴表示具有反射峰波段(如TM3或TM5)的情况下，根据几何意义，位于对角线(图1绿色虚线)上方的P(x，y)点必定有y＞x，即＞1．0;所以，根据遥感蚀变信息提取光谱特征的物理意义和上述约定，只有位于对角线上方的点才有可能满足“蚀变异常”的基本条件。

基于二维散点图的上述基本特性，可以将二维散点图用作分析遥感图像光谱数据空间几何结构特征的重要技术手段。

2 二维散点图类型划分与信息定位

在遥感蚀变信息提取中，必须注意所提取出来的“蚀变信息”要具有物理意义、统计意义和地质意义。物理意义是指“蚀变信息”要符合某类蚀变矿物的光谱特征;统计意义是指“蚀变信息”在所给的统计模型中是可分离(或可识别)的;地质意义则是要保证这些“蚀变信息”在野外地质查证时是能够做出相应地质解释的。二维散点图的空间结构分析就是为了保证在室内通过遥感图像处理提取出来的“蚀变信息”要具有物理意义和统计意义。

下面基于物理意义来对遥感图像数据的二维散点图进行5种类型划分，并分别做出相应的信息定位。

1)类型Ⅰ。散点图椭圆(背景椭圆)大部分位于对角线(蓝色虚线，下同)上方，且蚀变异常信息落在椭圆长轴左半区的边界上(图2)。

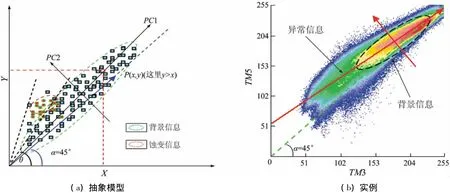
图2 类型Ⅰ的二维散点图Fig．2 2D scatter plot of type I

如图2所示，在各种自然景观区的遥感图像中，类型Ⅰ大多数是波段序偶(如TM3和TM1组合、TM5和TM7组合或TM5和TM3组合)二维散点图最主要的类型。当遥感图像出现该类型的二维散点图时，基于物理意义，可以认定蚀变异常只能出现在椭圆PC1轴左半区的边界上。

2)类型Ⅱ。散点图椭圆全部落在对角线上方，椭圆长轴的左右两侧边界上均可能出现蚀变异常信息(图3)。

图3 类型Ⅱ的二维散点图Fig．3 2D scatter plot of type II

如图3所示，类型Ⅱ是各种波段序偶二维散点图中较多出现的一种类型。在这种情况下，笔者提出了椭圆长轴的左右两侧边界上均可能出现“蚀变异常信息”的判断，即第二主成分(PC2)的2个端点处都有可能存在蚀变异常信息，因为它们均满足y＞x，即＞1．0的物理意义。

3)类型Ⅲ。散点图椭圆与对角线交叉、且椭圆长轴左半区边界上蚀变异常信息与干扰信息并存(图4)。

图4 类型Ⅲ的二维散点图Fig．4 2D scatter plot of type III

如图4所示，类型Ⅲ也是各种波段序偶二维散点图比较常见的类型。需要注意的是，这里对角线下方的椭圆第一象限边界存在的异常信息(即绿色虚线椭圆内的点群)为干扰信息，需要采用选择相关波段的办法予以剔除［6］。除了对角线上方且位于椭圆长轴左半区的边界存在蚀变信息之外，在对角线上方的椭圆第三象限边界上也有可能存在蚀变信息。

4)类型Ⅳ。散点图存在双椭圆(“背景”椭圆与“干扰”椭圆)分布形态(图5)。

图5 类型Ⅳ的二维散点图Fig．5 2D scatter plot of type IV

如图5所示，一旦遥感图像的自然景观区含有占一定面积比例的植被覆盖区，采用近红外与红光波段组合(如TM4，TM3波段组合)就一定会出现这种类型的散点图。其他波段同TM4组合的二维散点图也可能会出现这种类型，但形态一般没有如此典型。在对角线之上的“背景”椭圆四周边界上都可能存在蚀变信息。这种类型最复杂，用其提取蚀变信息也是最难的。如何解决此类复杂干扰问题参见文献［6］。

5)类型Ⅴ。散点椭圆全部落在对角线下方(图6)。

图6 类型Ⅴ的二维散点图Fig．6 2D scatter plot of type V

当遥感图像某个波段序偶的二维散点图出现如图6所示类型的情况时，可以从遥感图像数据的物理意义上判别该工作区没有具该波段序偶光谱特征的蚀变信息存在，或至少表明该工作区提取的该类蚀变信息可信度下降。例如，一旦TM5，TM7组合的二维散点图出现类型Ⅴ的情况，则可以从遥感图像数据物理意义上判别该工作区无羟基蚀变或碳酸岩化信息存在。

上述5种类型已经基本包括不同自然景观区遥感图像可能出现的二维散点图的绝大多数形式，但每种类型都可能存在一些近似的变形，需要在实践中认真观察与分析。

3 二维散点图空间几何结构分析与遥感蚀变信息提取方法选择

遥感图像二维散点图的空间几何结构包括宏观几何结构与微观几何结构。前者指散点图回归线斜率及其总体几何形态;后者指背景、干扰与蚀变信息在散点图中的聚类空间展布及其相互关系。依据二维散点图不仅能够定位出遥感图像的背景、干扰与蚀变信息［6］，而且可以帮助实现遥感蚀变信息提取方法的选择。

众所周知，波段比值与主成分分析是遥感蚀变信息提取的2种重要方法。但是，什么情况下应该采用何种方法，依然让人困惑［9］。笔者根据对二维散点图空间几何结构与波段比值的关系，以及多年实践经验总结得到如下3点认识:①若由遥感图像某个波段序偶生成的二维散点图的回归线斜率较小(即远远小于1．0时，如类型Ⅲ的形态)，则采用波段比值法效果差，并且提取的“蚀变信息”会混入诸如阴影、水体等干扰信息;反之，如果回归线斜率较大，则采用波段比值的效果较好;②一旦波段比值法适用，其提取遥感蚀变信息的效果比主成分分析好;③任何情况下，主成分分析比波段比值提取遥感蚀变信息更稳健，但不一定是最佳。

下面通过一个应用实例来进一步论述二维散点图空间几何结构与波段比值的关系。

青海省巴音山地区属于高寒山地，分布有多个金属矿床与矿点。该地区在TM遥感图像上岩石出露较好，但也存在比较严重的植被、水体与荒漠区干扰。

图7是由巴音山地区TM5和TM4波段组合得到的二维散点图，属于类型Ⅰ。

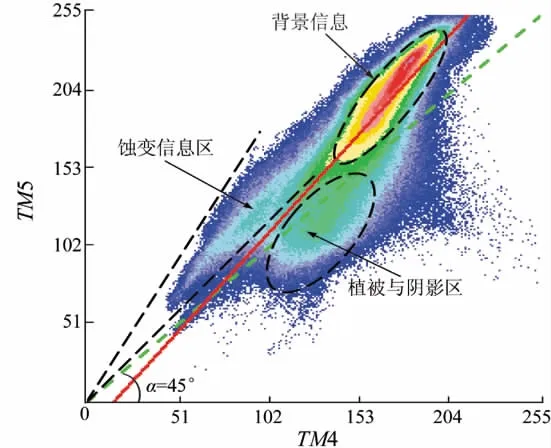
图7 波段比值在二维散点图上的几何解释Fig．7 Geometric explaination of band ratio on 2D scatter plot

从图7可以看出，若存在TM5＞TM4类型的蚀变信息，则应该位于对角线之上、“背景”椭圆之外的区域，而植被与阴影等主要干扰信息则应在回归线的另一侧。很明显，在图7中能够定位出“背景”、“干扰”与“蚀变信息”;而图7中的2条黑色虚线与坐标原点构成的扇形区(即“蚀变信息区”)，恰恰是波段比值的高值范围。

图8是由TM5/TM4增强方法提取的该地区遥感蚀变异常信息图像。经野外地质验证，除了哈莉哈德山2个异常由于海拔太高未做检查(见图中“待查证的异常”)和沙柳河下游地区为带状分布的蚀变矿物淤积物外，其他蚀变异常信息都与已知矿床、矿点对应得很好。其中，太子沟铜锌矿与东山铜矿对应于一级强度蚀变异常，钻石沟和东沟2个铅锌矿对应于二级强度异常。该地区铜锌矿区带主要蚀变矿物为黄钾铁矾、石英、透辉石、方解石、绢云母和绿泥石等;铜矿区段主要蚀变矿物为黄钾铁矾、褐铁矿、石英、绢云母和绿泥石等;铅锌矿区段主要蚀变矿物是褐铁矿、黄钾铁矾、孔雀石、石英和方解石等。

图8 青海巴音山地区TM 5/TM 4提取的蚀变异常信息Fig．8 Alteration abnormal information extracted from TM 5/TM 4 in Bayin Mountain region in Qinghai

图9是由巴音山地区TM5和TM7波段组合得到的二维散点图，属于类型Ⅱ。

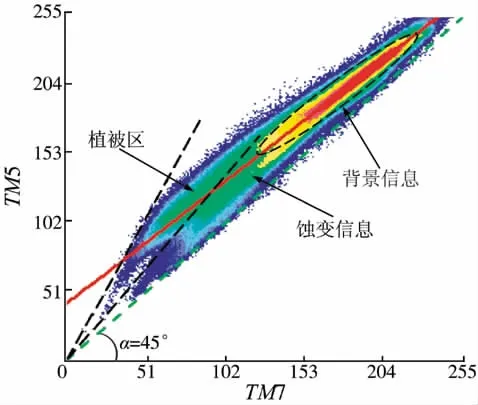
图9 二维散点图中信息定位Fig．9 In formation location in 2D scatter plot

一般情况下，采用TM5和TM7两个波段提取羟基蚀变信息，要么是运用波段比值进行增强，要么是用主成分分析的第2主成分提取高值部分作为蚀变信息。但是，从图9中不难看出，若用TM5/TM7增强方法，提取得到的必然是植被信息，而非羟基蚀变信息。所以，这种情况下，波段比值方法是不适用的。类型Ⅱ的二维散点图特征表明，此种情况下具有物理意义的蚀变信息有可能出现在回归线右侧下方且对角线的上方区域。

图10是由TM5和TM7波段主成分分析第2主成分低值端得到的羟基蚀变信息图像。

图10 青海巴音山地区TM 5和TM 7波段主成分分析提取的蚀变异常信息Fig．10 Alteration abnormal information extracted from PCA of band TM 5 and TM 7 in Bayin Mountain region in Qinghai

由于干扰的原因，该地区采用TM5和TM7两个波段主成分分析尽管能够提取出一些羟基蚀变信息，但不是最佳的方法，远没有采用TM5/TM4运算提取的蚀变信息(图8)效果好。

综上所述，由遥感图像不同波段序偶得到的二维散点图，其空间几何结构决定了背景、干扰与蚀变信息的空间展布与定位，也决定了提取遥感蚀变信息应该如何选择更合适的波段组合与技术方法。

4 结论

1)遥感图像的二维散点图是表达2个波段组合光谱空间结构信息的最佳图示方式，其丰富的空间几何结构信息值得认真研究与分析。

2)基于物理意义对遥感图像二维散点图类型进行划分，使得每一种类型的二维散点图都可以定位出具有相应光谱特征意义的蚀变信息，从而保证所提取的遥感“蚀变信息”具有物理意义。同样，在不同类型的二维散点图上能够确定出相应遥感图像的“背景”、“干扰”与“蚀变异常”信息，从而明确了“蚀变异常”信息在统计空间上的可分离性。

3)依据二维散点图空间几何结构的宏观与微观特征，能够正确选择最佳的遥感蚀变信息提取方法。

4)通常情况下，遥感蚀变信息提取的波段选择往往局限于关注蚀变矿物的诊断谱带，而忽视了光谱曲线的整体形态变化特征。在青海巴音山地区的应用实例中，用TM5和TM4波段组合提取的遥感蚀变信息远好于常规的TM5和TM7波段或TM3和TM1波段组合。笔者在实际工作中已取得不少类似的例子，表明遥感蚀变信息提取不能仅局限于常规波段组合。

［1］ 张远飞，吴德文，张艮中，等．高光谱数据的波段序结构分析与应用研究［J］．国土资源遥感，2010，22(1):30－38．Zhang Y F，Wu D W，Zhang G Z，et al．Study on band sequence structure analysis of hyperspectral data［J］．Remote Sensing for Land and Resources，2010，22(1):30－38．

［2］ 张远飞，吴德文，袁继明，等．遥感蚀变信息多层次分离技术模型与应用研究［J］．国土资源遥感，2011，23(4):6－13．Zhang Y F，Wu DW，Yuan JM，et al．The model and application of multi－level detaching technique of remote sensing alteration information［J］．Remote Sensing for Land and Resources，2011，23(4):6－13．

［3］ 张远飞，袁继明，朱谷昌，等．基于遥感数据随机模型的空间结构分析与蚀变信息提取［J］．国土资源遥感，2010，22(4):34－39．Zhang Y F，Yuan JM，Zhu G C，et al．A study of spatial structure analysis and alteration information extraction based on random models of remote sensing data［J］．Remote Sensing for Land and Resources，2010，22(4):34－39．

［4］ 张远飞，杨自安，张普斌，等．高(多)光谱数据的背景－异常子空间模型研究［J］．地球信息科学学报，2009，11(3):282－290．Zhang Y F，Yang Z A，Zhang P B，et al．Research on background－anomaly sub－space model of hyper(multi－)spectral data［J］．Journal of Geo－Information Science，2009，11(3):283－290．

［5］ 冈萨雷斯，伍兹．数字图像处理［M］．朱志刚，林学阎，石定机，等译．北京:电子工业出版社，2002．Castle man K R，Woods F E．Digital image processing［M］．Zhu Z G，Lin X Y，Shi D J，et al．Translated．Beijing:Publishing House of Electronics Industry，2002．

［6］ 张远飞，袁继明，朱谷昌，等．遥感蚀变信息提取中的干扰因素研究与消除对策［J］．遥感信息，2010(6):3－9．Zhang Y F，Yuan JM，Zhu G C，etal．Study and elimination of the interfering factors in remote sensing alteration information extraction［J］．Remote Sensing Information，2010(6):3－9．

［7］ Small C．The Landsat ETM+spectral mixing space［J］．Remote Sensing of Environment，2004，93(1/2):1－17．

［8］ 徐 桃．基于光谱数据空间结构特征分析的遥感蚀变信息提取研究［D］．长沙:中南大学，2011．Xu T．Research on extraction alteration information of remote sensing based on spectral space data analysis［D］．Changsha:Centre South University，2011．

［9］ 张玉君，曾朝铭，陈 薇．ETM+(TM)蚀变遥感异常提取方法研究与应用——方法选择和技术流程［J］．国土资源遥感，2003，15(2):44－49．Zhang Y J，Zeng ZM，Chen W．The methods for extraction of alteration anomalies from the ETM+(TM)data and their application:Method selection and technological flow chart［J］．Remote Sensing for Land and Resources，2003，15(2):44－49．