城市人口空间分散与经济增长——基于特大城市的实证分析

◎ 蔡寅寅 孙斌栋

一、文献综述

集聚对经济增长的重要作用已得到无数学者的证明：Masahisa Fujita and Paul Krugman（1995）[1]，Ciccone， A. and Hall R（1996）[2]，Baldwin ，Martin and Ottaviano（2001）[3]，Henderson（2003）[4]等分别从机制和实证分析上给出了肯定的答案。但还有一部分实证研究得出了截然相反的研究结果，Carlino（1979）通过研究发现，人口规模与生产率存在负相关，这就意味着存在聚集不经济[5]；Futagami和Ohkusa（2003）的研究以人口规模作为集聚的代理变量，发现它与经济增长率之间是存在着倒U型关系[6]。

可见集聚对经济增长的影响不仅仅是线性如此简单，更确切的说它对经济的影响更倾向于倒U型，即在一定城市规模内，集聚对经济增长具有促进作用，而超出了一定的门槛值，就会出现集聚不经济。

因此又有学者针对这个门槛值研究了城市最优规模问题，Anas (2002)将城市内部空间结构纳入新经济地理学模型的框架，考察了最优城市规模，最后得出，随着城市总人口规模的增加，最优的城市规模不断缩小，即经济的集聚程度不断降低，最终可能导致所有经济活动趋向完全分散[7]。有学者试图计算出集聚不经济的分界点，如Yoshitsugu Kanemoto（1996）通过分析得出东京的规模过大，一旦城市人口超过40万人，规模效益将递减[8]；Marius Bruelhart（2008）调查了国家层面的经济活动空间集聚的影响，用各个国家超过75万的城市人口占总人口的比重和城市化水平以及泰尔指数作为代理变量，通过对105个国家自1960-2000年的面板数据分析，发现集聚促进经济增长是在一定经济发展水平上的，大约在人均生产总值1万美元左右[9]。此外，ZhengXiao Ping(1998)[10]，Capello and Camagni(2000)[11]等通过实证分析也得到了最优规模的分界点，但得到的分界点却各不相同。目前无论是从成本效益理论出发，还是实证研究出发，都未能得到一个相对稳定的分界点，但是可以肯定的一点是随着城市规模的不断扩大，规模效益不会永远随之增长。

国内学者如王小鲁和夏小林(1999)[12]，马树才和宋丽敏(2003)[13]，周国富、黄敏毓(2007)[14]，张应武（2009）[15]，肖文和王平（2010）[16]等以我国城市或省为样本进行了集聚经济的实证分析，发现集聚经济在一定的规模范围内确实对我国经济增长起到了重要促进作用，但是超出一定规模范围，其经济效益有待考证。

到目前为止实证研究的结果存在一定分歧，一方面是因为进行实证分析的样本范围存在较大差异，有些实证以国家为对象，而有些则以省、州或市为研究对象，这必然会引起结果的差异，虽然不能否认无论是国家还是区域都存在着集聚经济，但是城市可能会是更合适的研究单位；另一方面，选择的代理指标不一致，集聚的代理变量主要集中在人口和就业规模、密度[17,18]，也有学者用经济密度和中心化指标[19]来衡量，其中韦亚平和赵民（2006）提出了空间结构的绩效测度方法，建立了绩效密度、绩效舒展度、绩效人口梯度及绩效OD比等指标[20]，但只是停留在理论阶段。从某种程度上来讲这些指标都存在一定的缺陷：人口规模大的城市不一定集聚程度就高，人口密度大的城市不一定能形成规模经济，而经济密度与经济增长则存在太强的互为因果联系。

此外，以往研究都着重从集聚的角度来讨论问题，而忽视了从分散角度来分析经济绩效。因此针对城市是否存在集聚不经济，分散是否更有利于经济增长这个困惑，本文特别从人口空间分散的角度进行了实证研究。择取了34个特大城市及以上的城市市区作为研究对象，着重探讨城市内部人口空间分散对经济绩效的影响。选取的指标数据均来自《2011年中国城市统计年鉴》及各城市的《第六次人口普查公报》。主要使用stata统计软件进行相应的统计分析。本文假设特大及巨大城市已开始出现集聚不经济，而人口的适度分散则有利于促进经济增长，但是过度分散并不利于经济增长。

二、模型的构建

（一）样本选择

本文假设规模越大的城市越可能倾向分散化发展，基于以下3点原因：1.城市环境压力、交通压力、生活成本随着规模的扩大而不断增加，使得城市的人口逐渐向成本低的地区转移；2.随着城市轨道交通的不断发展，增加了城市内部的交通通达性，提高了出行便捷度，降低了人们的出行成本；3.现代科技的发展，尤其是通讯技术的发展，减少了物理接近的重要性，实现了人们可以不必出行在家进行工作的可能性。

因此考虑到城市规模越大，分散的作用越有可能体现出来，本文择取了特大城市及以上的城市作为研究对象。依据《中小城市绿皮书》提出的划分标准：市区常住人口50万以下的为小城市，50万～100万的为中等城市，100万～300万的为大城市，300万～1000万的为特大城市，1000万以上的为巨大型城市，选取了市区常住人口300万以上的城市作为研究样本。此外，城市集聚一般首先从城市内部开始，而出现集聚不经济也非常有可能从内部开始，因此本次研究的范围是界定在城市内部，即市区范围内，不包括下面的市县。

（二）人口分散指标的测度

不同于以往的代理变量，本文对人口的空间分散进行了深入测度。其测度公式为：

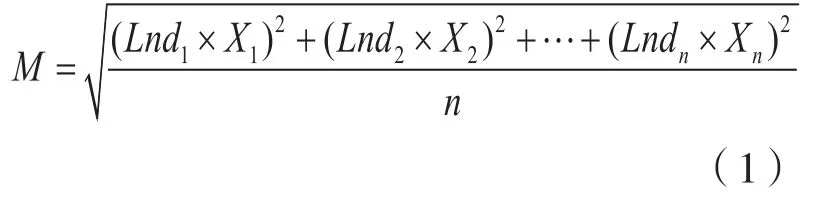
x1-xn表示各个区的人口标准化数，通过计算出每个城市人口密度最高的区，选择这些区作为人口中心区，将其人口赋值为1，其他区则以人口中心区为标准，得到标准化数据；d1-dn为距离，即人口中心区到各个区之间的距离，由于无法获取各个区具体的人口分布状况，因而无法确定各个区的人口重心，因此选择以各个区的区政府所在地为基本点（一般而言区政府所在地区往往是人口较为密集的地方），通过Google地图测量得到各个区政府到人口中心区政府的距离；最后将人口标准化数据与距离的对数相乘，得到一个平均平方数M。M代表的是城市内部人口的分散程度，若M越大，则表明城市内部的人口越分散，M越小则表明城市内部人口越集聚。

之所以构建这样一个指标来作为人口分散的代理变量，理由如下：

以人口中心区为1，实际上表现出了“位序关系”，相当于所有的分区人口都除以最高区人口，得到一个标准化数。这个标准化数是各个区相对于人口中心区的比较结果，数值越高意味着人口越接近中心区，而高数值区的数量会影响人口空间分布状况。假设人口第二大区与人口中心区的人口规模相差不大，那么就表示城市可能越趋向双中心分布；若人口第二大区、第三大区与人口中心区的人口数量非常接近，这就意味着城市可能有三个人口中心；反之若人口第二大区与人口中心区的人口规模差距非常大，城市就可能越倾向高度集聚。如果式1中x1-xn的值都比较大的话，M的值也会相应变得较大，也就意味着人口越趋向分散分布，反之若X1-X2的值都较小，M值也会变小，人口就越趋向集中分布。

除此之外，式1中还加入了距离的对数变量，因为若其他区与人口中心区间的距离过近，很容易形成连片发展，很难形成真正意义的分散。距离不仅可以表现出各市辖区中心与城市人口中心区的远近关系，同时还充当着权重的角色，传达出来的意思是人口分布在距离越远的地方，越趋向于分散。但是这可能存在一定问题，由于这里的距离为城市各区政府之间的距离，而不是人口重心间的距离，就可能导致一些偏差。不能否认可能存在个别区的区政府与中心区政府的距离虽然非常远，但比之其他区在实质上并未表现出更加分散。为了相对减少这种计算误差，对距离进行了对数处理，相对缩小了距离之间的差距，减小权重的影响作用，但同时又不妨碍反映远近关系。

（三）模型的建立

根据以往的实证研究，结合本文的研究对象，选取了6个解释变量，分别为：资本、劳动力、人力资本、制度、人口空间分散和交通。所有的指标均为人均化后的指标。

通常而言反映经济绩效的指标为GDP或人均GDP，这里选取人均GDP作为经济绩效的代理变量，为模型的被解释变量G，等于市区GDP/市区常住人口；资本（K）是柯布道格拉斯模型中最基本的要素之一，一般会选择资本存量来反映资本对经济增长影响，本文用永续盘存法进行计算，以5%作为折旧率，计算了2001年-2010年的资本存量，并进行人均化；劳动力(L)用人均劳动力来表示，即劳动力占总人口的比重，更能反映我国城市的人口结构；人力资本（H）选取了六普公报中提供的每十万人拥有大学生数来表示；自改革开放以来，我国的经济得到快速发展，不可否认制度改革的重要性，本文选择政府作用（I）来表示制度的影响，由政府支出减去科教支出/GDP的比值计算得到，表现了政府的控制；交通（T）用人均拥有道路面积表示。

根据所选取的被解释变量和解释变量，建立了广义柯布道格拉斯模型：

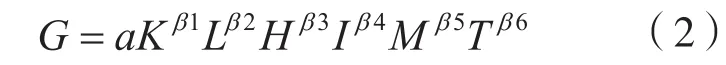
将模型进行对数化得到：

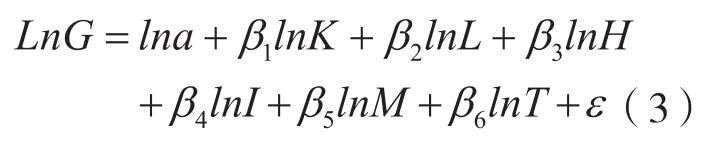
三、实证分析

（一） OLS回归模型的前提检验

在进行OLS回归模型前，先进行模型的正态性、异方差性及残差独立性检验，以确定模型是否满足假设条件，确定用OLS进行回归分析的可行性。

表中Shapiro -wilk w test未通过显著性检验，说明模型接受原假设，为正态模型；DW检验值为1.93，接近于2，说明模型的残差与变量互为独立；White检验未通过显著性检验，接受原假设，模型为同方差，无异方差；VIF小于5，表明模型不存在着严重共线性；Ramsey reset检验了模型遗漏变量或函数误设问题，其值为0.44，未通过显著性检验，接受原假设：模型不存在遗漏变量问题。通过以上检验表明可以用OLS进行回归分析。

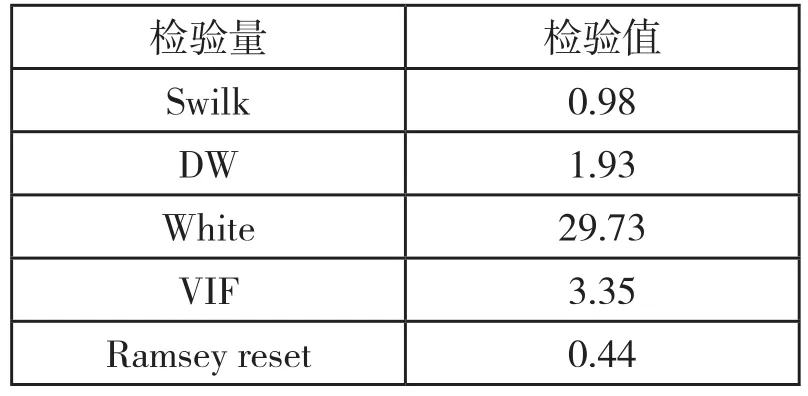
表1 模型假设条件检验

（二）回归分析结果

OLS1 和OLS2的回归分析结果显示，拟合R2由0.6046上升到0.6782，说明人口分散在这个模型中具有重要的作用。OLS2回归结果显示资本、人口分散和交通都通过了显著性检验。资本通过了0.01的显著性检验，人口分散和交通均通过了0.05的显著性检验，与经济增长呈现出正相关。人力资本、劳动力和制度均未通过显著性检验。

回归结果反映出目前中国仍然处于投资拉动经济增长的阶段，投资对经济增长的贡献率达到0.43。交通基础设施作为城市经济发展的必要保障，对城市的产业发展、规模布局产生了重要作用，对经济增长产生了积极影响。

人口分散对经济增长起到了积极的作用，每增加一个单位的分散，人均生产总值就会增加0.167个百分点，验证了本文开始的假设。随着城市规模的不断扩大，城市内部的交通压力、人口压力、住房和环境等压力也会随之变大，如果再继续无限制集聚下去，必定会引起更多的问题。因此城市发展不应盲目追求集聚经济，而是要适度分散发展。

新经济增长理论认为在知识经济时代人力资本对经济发展具有更为重要的意义，但是人力资本在中国特大城市中却没有显示出价值，究其原因主要是中国的产业大多处于较低端的位置，人力资本的作用尚未发挥出来。劳动力是道格拉斯函数最基本的要素之一，也是被广泛认可的一个要素，一直以来中国凭借其人口红利使经济得到了快速发展，但是对特大城市来说，传统的经济增长方式已不能适应城市的发展，依靠人口红利来拉动经济增长的时代即将过去。

（三）过度分散问题的探讨

回归分析的结果表明，人口的空间分散有利于城市经济增长，但是通过spline函数模拟曲线后，发现人口分散与经济增长之间呈现出倒U型曲线，也就意味着过度的分散可能会导致对经济增长的消极影响。这一点从理论来讲是合乎一定逻辑性的，过度的分散可能会引起效率的降低，因此考虑到有可能出现的问题，需要对过度分散进行验证。

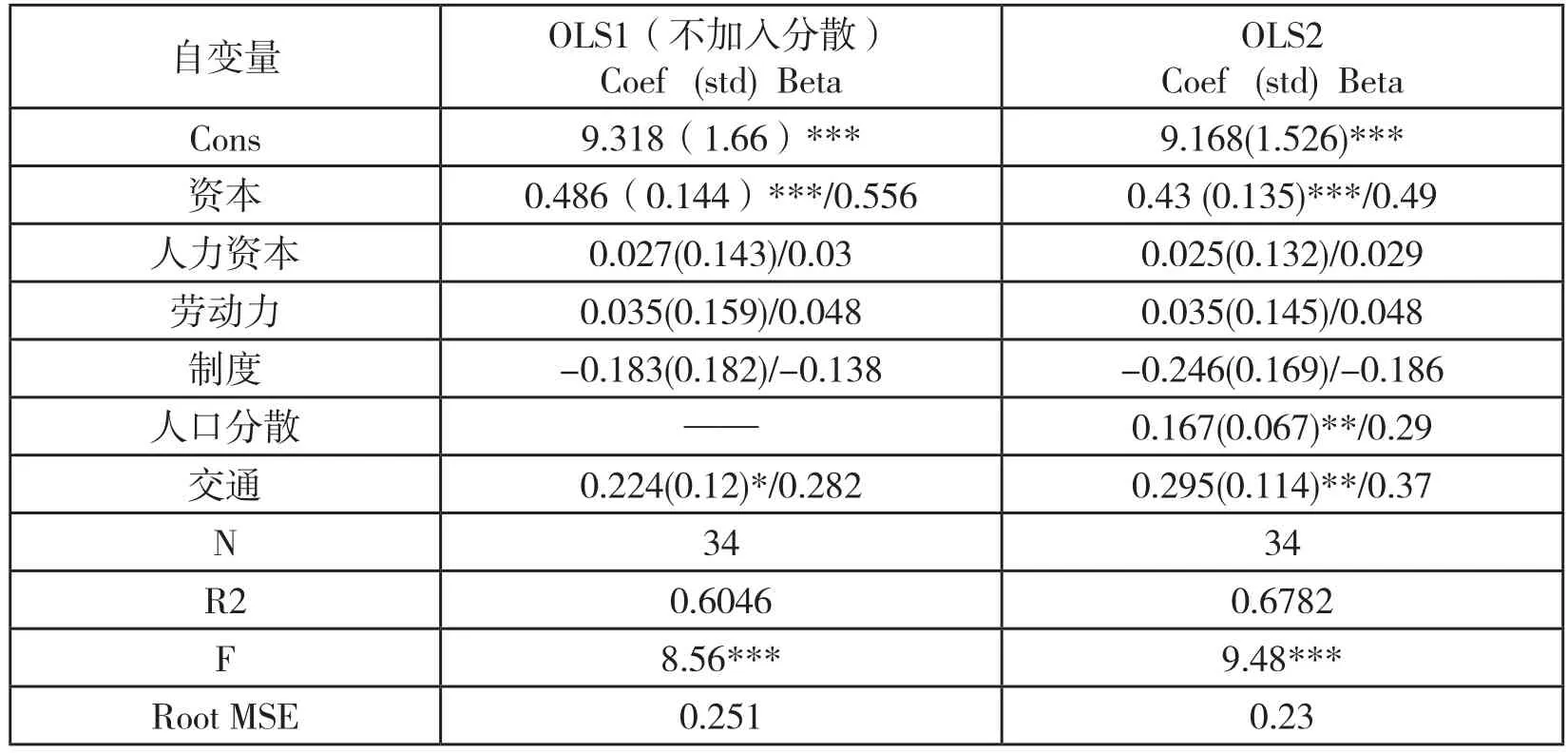
表3 OLS回归 和2SLS回归结果

既然人口分散与经济增长呈现出非线性，那么需要在模型中加入人口分散的二次项，从而形成多项式回归。多项式回归1中，只加入两个解释变量，即人口分散和人口分散的平方；多项式回归2中剔除了OLS回归中不显著的变量，只选择通过显著性检验的变量进入模型（减少其他因素的影响）。回归结果显示，模型1中人口分散和人口分散的平方均通过了0.05的显著性检验，且相关系数为一正一负，表明人口分散可以促进经济增长，而人口的过度分散则不利于经济增长；模型2中人口分散通过了0.01的显著度检验，回归系数为正，再次验证了人口分散对经济增长的积极影响；人口分散的平方虽然通过了0.1的显著度，但相比较资本、交通等因素而言，过度分散的影响并没有那么显著，或者说资本、交通等因素可能在一定程度上削弱了过度分散带来的负面效应，但目前并没有强有力的实证分析可以证明这一点，这是未来需要继续深入研究的内容。

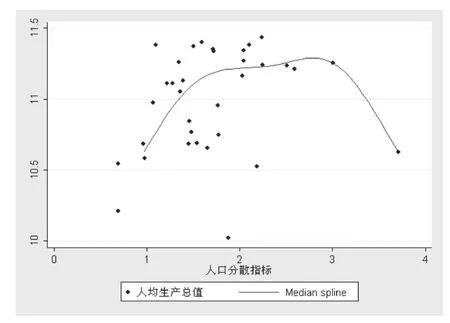
图1 样条曲线

四、结论与启示

本研究采普通最小二乘法、spline函数及多项式回归等统计方法，得到了以下结论：

1.特大城市内部人口空间分散的经济绩效已体现出来，人口分散对经济增长具有积极作用。因此对于这些城市而言，要考虑的可能不是继续扩大规模，一味追求集聚经济，而应当适当的分散人口，缓解城市的发展压力。

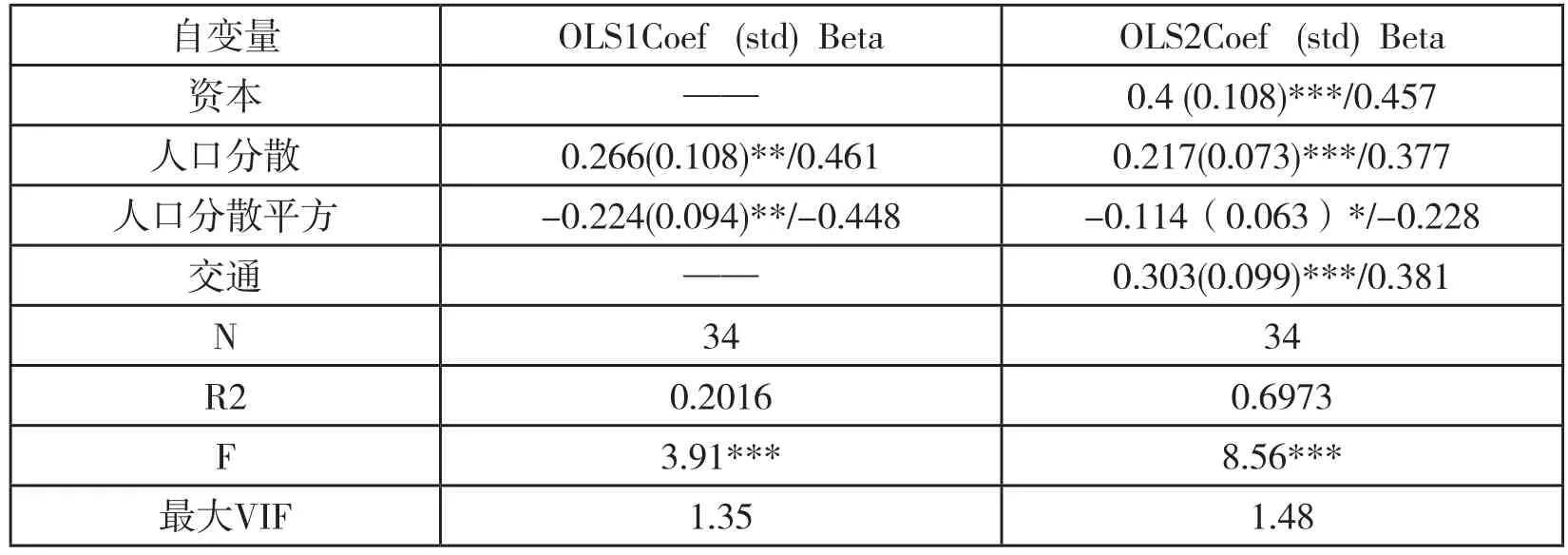
表4 多项式回归结果

2.实证研究还表明，过度分散并不利于城市经济增长，但是资本和交通可能会降低过度分散的影响，也就意味着对于过度分散的地区而言，可以通过加强地区的交通建设，完善交通通达性，加强资本的投入来弥补这个问题。

3.资本对我国经济发展仍然起到了非常重要的作用，验证了中国主要靠投资拉动经济的现状。但是拉动经济增长的是三驾马车，而不应该是资本独大，因此不能一味依赖于资本的拉动作用。

4.目前劳动力和人力资本对特大城市的作用并不显著。因此未来城市发展应加快发展方式转型、产业优化升级，充分发挥出人力资本的作用。

5.交通水平对经济增长的影响是显著的，因为交通通畅与否会影响资本、劳动力的流动，资源的组合方式。因而城市发展应充分认识到交通的作用，进一步完善交通基础设施建设，提高城市道路的运行效率，这不仅可以缓解交通拥堵，而且对城市分散具有推动作用，对城市经济增长至关重要。

[1]Masahisa Fujita, Paul Krugman. When is the economy monocentric? von Thiinen and Chamberlin unified[J]. Regional Science and Urban Economics, 1995(25): 505-528.

[2]Ciccone A, Hall R. Productivity and the Density of Economic Activity[J]. American Economic Review,1996(1): 54- 70.

[3]R.E.Baldwin, P.Martin, G.Ottavinao. Global Income Divergence, Trade and Industrialization: The Geography of Growth Take- off [ J]. Journal of Economic Growth, 2001(1): 5-37.

[4]Henderson JV. The urbanization process and economic growth: the so-what question[J]. Journal of Economic Growth, 2003(1): 47-71.

[5]Carlino G.A. Increasing Returns to Scale in Metropolitan Manufacturing[J]. Journal of Regional Science,1979(19) : 363-373.

[6] Futagam i K, Ohkusa, Y. The Quality Ladder and Product Variety: Larger Economies May not Grow Faster[J]. Japanese Economic Review, 2003(54) : 336-351.

[7]Anas A. Vanishing Cities: What does the New Economic Geography Imply about the Efficiency of Urbanization ? Journal of Economic Geography , 2004( 2) 181－199.

[8]Yoshitsugu Kanemoto. Agglomeration Economies and a Test for Optimal City Sizes in Japan[J].the Japanese and International Economies, 1996, (10):379-398.

[9] Marius Brülhart, Federica Sbergami.. Agglomeration and growth: Cross-country evidence[J]. Journal of Urban Economics, 2009(65): 48-63.

[10]Xiao-Ping Zheng. Determinants of agglomeration economies and diseconomies:empirical evidence from Tokyo[J]. Socio-Economic Planning Sciences , 2001(35): 131- 1441.

[11]Capello R and R Camagn i. Beyond Optimal City Size: An Evaluation of Alternative Urban Growth Pattern. Urban Studies, 2000( 37 ): 1479-1497.

[12]王小鲁,夏小林.优化城市规模,推动经济增长[J].经济研究,1999(9):22-29.

[13]马树才,宋丽敏.我国城市规模发展水平分析与比较研究[J].统计研究,2003(4).

[14]周国富,黄敏毓.关于我国城镇最佳规模的实证检验[J].城市问题,2007(6):6-11.

[15]张应武.基于经济增长视角的中国最优城市规模实证研究[J].上海经济研究,2009(5):31-38.

[16]肖文,王平.外部规模经济、拥挤效应与城市发展:一个新经济地理学城市模型[J].浙江大学学报，2011(2):94-105.

[17]陈彦光,周一星.城市规模—产出关系的分形性质与分维特征——对城市规模—产出幂指数模型的验证与发展[J].经济地理,2003,4:476-481.

[18]张艳,刘亮.经济集聚与经济增长——基于中国城市数据的实证分析[J].世界经济文选,2007(1):48-56.

[19]陈林生,李刚.聚集效应、区位差别与区域经济增长[J].四川大学学报,2004(2):32-35.

[20]韦亚平,赵民.都市区空间结构与绩效——多中心网络结构的解释与应用分析[J].城市规划.2006(4)：9-16.