盾构掘进速度及非正常停机对地面沉降的影响

林存刚 ，吴世明，张忠苗 ，刘俊伟 ，李宗梁

（1. 浙江大学 岩土工程研究所，杭州 310058；2. 浙江大学 软弱土与环境土工教育部重点实验室，杭州 310058； 3. 杭州庆春路过江隧道有限公司，杭州 310002）

1 引 言

近些年，随国内地铁及水底隧道建设热潮的兴起，盾构法隧道施工技术越来越广泛地在全国各大中城市应用。盾构隧道多穿越城市建筑物及地下管线密集区域，对隧道施工引起的地层位移控制较为严格，因此，国内外众多学者对于盾构隧道施工引起的地层位移进行了广泛深入的研究，主要有经验公式法[1－3]、解析法[4－8]、模型试验法[9]及数值模拟法[10]等。这些研究考虑了施工方法、地层条件、隧道埋深及直径、盾构掘进参数的控制等多种因素对地面沉降的影响。然而，盾构掘进速度及非正常停机对盾构隧道施工引起的地面沉降的影响研究，国内外文献中鲜有报道。

本文由盾构掘进速度及停机时间确定盾构压重在其下卧土层中产生的附加应力的持续时间后，运用太沙基一维固结理论和单向压缩分层总和法计算在该作用时间内的沉降，应用Peck 公式建立起盾构下卧土层沉降与地面沉降的关系，并以杭州庆春路过江隧道地面沉降的实测数据对该理论进行了验证。

本文仅考虑盾构掘进速度及非正常停机时间对盾构隧道施工引起的地面沉降的影响，对隧道开挖基底土体回弹、掘进参数控制等其他因素不加以考虑。

2 相关研究

Rowe 等[6]、Clough 等[11]对美国第1 条土压平衡盾构隧道施工引起的地面沉降分析认为，盾构长时间在某一断面搁置，会加剧该断面的地面沉降。盾构离开监测断面5 个月之后的隧道轴线位置地面沉降如图1 所示[6,11]。

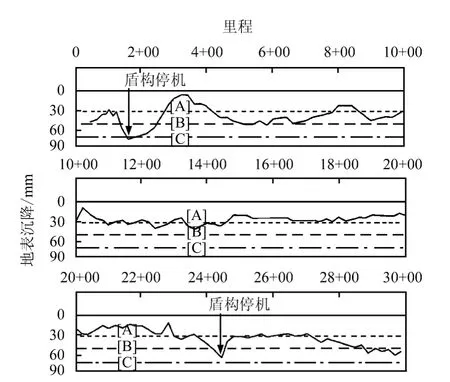
图1 隧道轴线位置地面沉降 Fig.1 Surface settlement profile along centerline of tunnel alignment

由图1 可见，沿隧道轴线位置里程1+60 和24+50 附近地面沉降最大，约为76 mm。盾构在里程1+160 位置停留15 d 进行动力系统与盾构机的连 接；盾构穿越木桩后有大量木屑残留在刀盘缝隙中，在里程24+50位置停留进行清理。Clough等[11]认为，该两处位置发生较大地面沉降和盾构在这两处长时间停留有关。

Rowe 等[6]认为，盾构停机时，由于土体的固结或水土压力的重分布，盾构土仓压力逐渐减少，由此引起较大的开挖面地层损失，进而加剧地面沉降。

除此[6,11]之外，鲜有关于盾构掘进速度及非正常停机对地面沉降的影响研究，并缺少相关的理论解释。

笔者认为，盾构长时间停机导致地面沉降加剧的原因，除盾构切口压力损失引起开挖面地层损失外，还有盾构压缩下卧土层引起固结沉降，该固结沉降持续时间由盾构掘进速度和停机时间确定。

3 计算模型的建立及求解

3.1 盾构下卧土层沉降计算

盾构在地层中掘进，计算模型纵剖面如图2 所示。

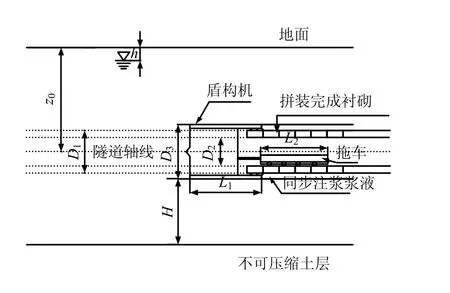
图2 盾构地层中掘进计算模型（纵剖面） Fig.2 Calculation model of shield tunnelling in soils（longitudinal profile）

如图2 所示，盾构在地层中掘进，z0为隧道轴线埋深(m)，D1为隧道外径(m)，D2为隧道内径(m)；D3为盾构机外径（开挖直径）(m)，L1为盾构机主机长(m)，L2为拖车长(m)，L 为盾构主机和拖车总长(m)，L=L1+L2，Wshield为盾构主机和拖车总重(kN)；h 为地下水位位于地表以下的深度(m)，H 为盾构机底部距离不可压缩土层（卵石层、碎石层或基岩）的长度(m)；假定自地面至不可压缩土层为均一地层，rsoil为土体重度(kN/m³)；rlining为衬砌管片重度(kN/m³)，rgrout为同步注浆浆液重度(kN/m³)，rw为地下水重度(kN/m³)。

图2 计算模型对应横断面见图3。

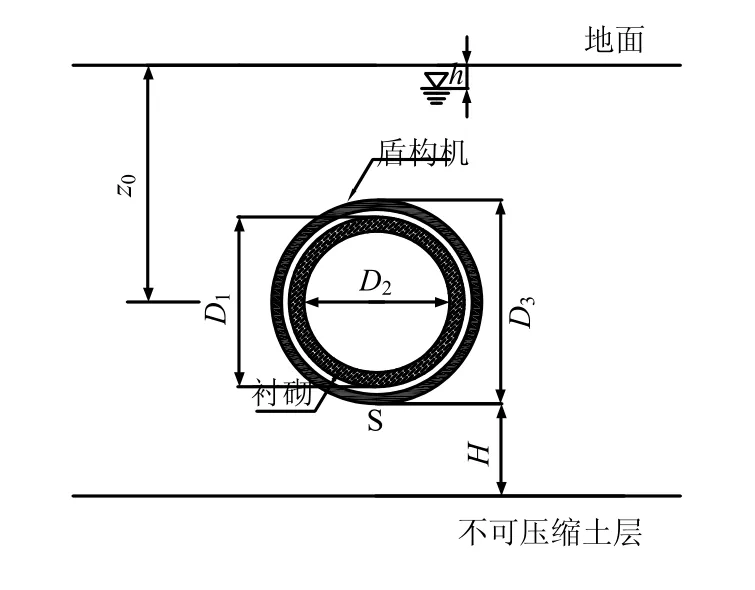
图3 盾构地层中掘进计算模型（横断面） Fig.3 Calculation model of shield tunnelling in soils（transverse section）

Verruijt 等[12]认为，由于建成隧道的重量小于开挖土体的重量，会在隧道底部产生“浮力效应”，该“浮力效应”会对隧道开挖引起的地面沉降产生影响。通过建立隧道在均质各向同性土体中开挖的弹性半平面模型，仅考虑地层损失和“浮力效应”，通过复变函数方法求解得出隧道开挖引起的横断面地面沉降。计算结果显示，“浮力效应”会对隧道开挖引起的地面沉降产生影响，建成隧道相对于开挖土体越轻，地面沉降将越小，且横向地面沉降槽宽度较仅考虑地层损失时计算所得沉降槽要窄；考虑“浮力效应”后，计算所得沉降槽与实测值更吻合。Verruijt 等的分析不考虑扰动土体固结，土体发生弹性变形，瞬时完成，与时间因素无关。

笔者认为，不仅开挖土体与建成隧道的重量差会对隧道开挖引起的地面沉降产生影响，而且盾构与建成隧道的重量差也会对其产生影响，且该影响与盾构掘进速度和停机时间相关。

不计扰动土体超孔隙水压力的消散，仅考虑开挖出土体与盾构及成型管片重量差引起的盾构下卧土体的应力释放，短期内盾构机底部S 位置（见图3）土体有效应力经历了4 个阶段：

（1）应力状态0 为初始应力状态0σ

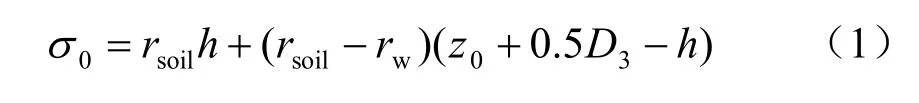
（2）应力状态1 为土体挖出后土应力1σ

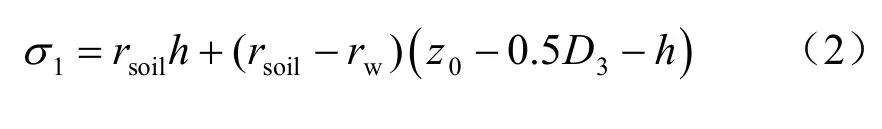
（3）应力状态2 为盾构机置换开挖出土体后土应力2σ

盾构机置换土体重量为Wsoil

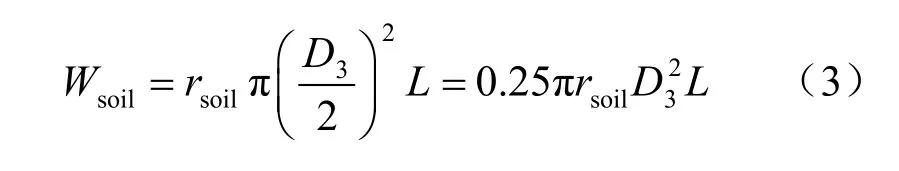
定义盾构机与其置换土体重量比为1λ ：

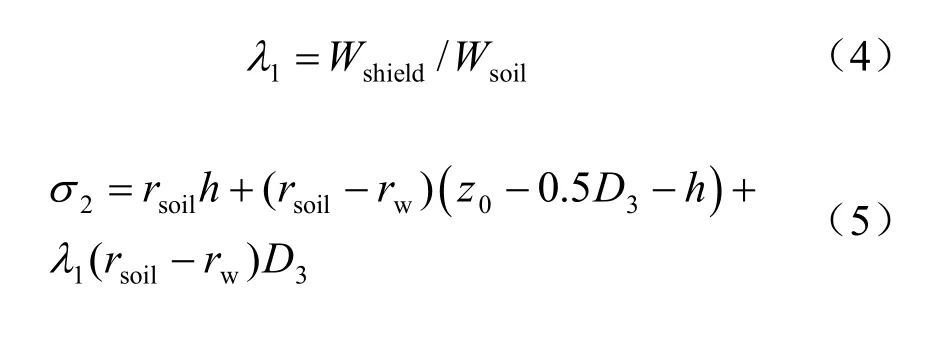
（4）应力状态3 为盾尾脱离，拼装成型管片和同步注浆浆液置换开挖出土体后土应力3σ

拼装成型管片和同步注浆浆液沿隧道轴线方向L 长度重量为Wlining：

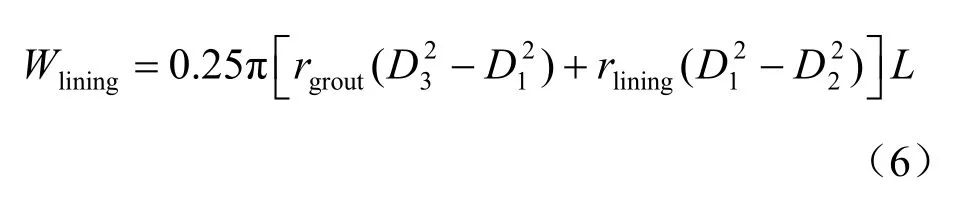
定义拼装成型管片和同步注浆浆液重量与其置换土体重量比为2λ ：

由于盾构机的重量及拼装成型管片和同步注浆液的重量与置换出的土体重量不相等，即 λ1≠1，λ2≠1，所以盾构通过以及离开时，对其底部土体加载或卸载，土体瞬时发生弹性压缩或回弹。该土体变形瞬时完成，可由弹性理论近似求得，与时间因素无关，与上述各有效应力状态维持时间长短无关，因此，与盾构掘进速度及停机时间相关性不大。盾构掘进速度及停机时间不影响隧道下卧土层因加载或卸载（应力状态σ0转化为σ1，再转化为σ2，最后转化为 σ3）引起的土体弹性变形，因此，本文研究盾构掘进速度及停机对地面沉降的影响时，未考虑盾构底部土体因加载或者卸载引起的土体弹性变形。

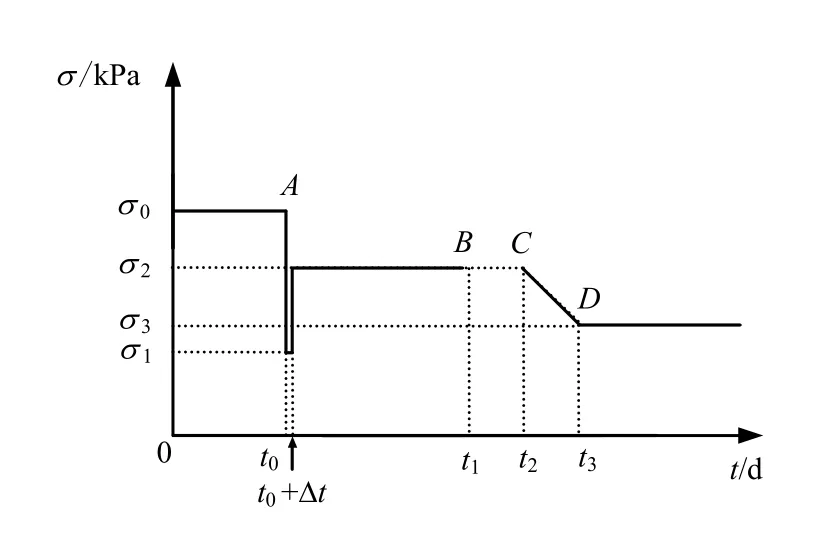
图4 盾构底部土体有效应力变化 Fig.4 Changes of effective soil stresses beneath the shield

图4 表示任一断面X 盾构底部S 位置土体有效应力随盾构机掘进的变化。图中，t0时刻盾构切口到达该断面，t2时刻盾构拖车尾部离开该断面。

图中Δt 相对较小，忽略不计。

考虑到附加应力的扩散，盾构拖车离开X 断面时，其隧道下卧土层仍受到盾构压重的影响；假定随着盾构逐渐远离土体有效应力线性递减，至拖车尾部离开10 m 盾构压重的影响已完全消失。即图4中，t3时刻对应拖车尾部离开X 断面10 m。

图4 中虚线段BC 对应盾构在X 断面停机时间tstop。

设盾构通过X 断面前后掘进速度为v(m/d)，则：

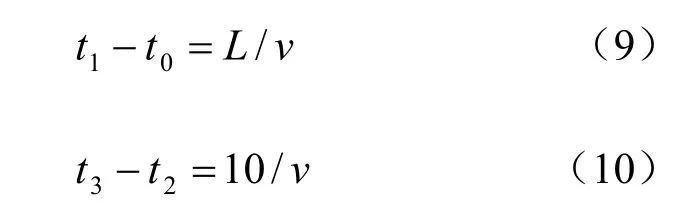
为简化计算，图4 转化为图5。

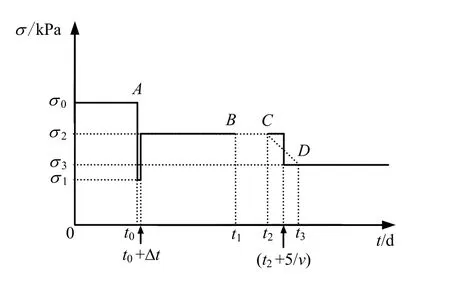
图5 盾构底部土体有效应力变化(简化后) Fig.5 Changes of effective soil stresses beneath the shield（simplified）

X 断面2σ 持续时间 2tσ：

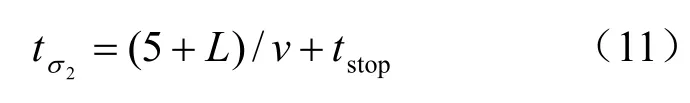
土体经开挖，由初始应力状态0σ 转变为1σ ，随后盾构压重相对于 1σ 应力状态施加附加应力2σΔ ；盾构远离后管片拼装完毕，管片压重相对于1σ 应力状态施加附加应力 3σΔ 。由 2σΔ 和 3σΔ 共同作用t 时间段下盾构下卧土层沉降St：

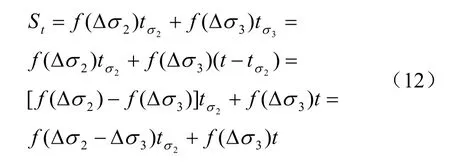
式中：f (Δ σi)tσi为附加应力 Δσi相对于应力状态σ1作用时间 tσi产生的土体沉降，i=2、3；[ f ( Δσ2)- f (Δ σ3)]tσ2表示 tσ2时间段内附加应力 Δσ2与 Δσ3相对于应力状态 σ1压缩盾构下卧土层产生的土体沉降差，等价于 tσ2时间段内附加应力 Δσ2与 Δσ3之差相对于应力状态 σ1压缩盾构下卧土层产生的土体沉降，即 [ f (Δ σ2-Δσ3)]tσ2，亦等价于 tσ2时间段内应力状态 σ2相对于应力状态 σ3产生的附加应力压缩盾构下卧土层产生的土体沉降。

由式（12）可见，从盾构切口到达开始，任意时刻t某一断面盾构下卧土层的沉降，仅与 2tσ相关，即应力状态2σ 持续时间。而由式（11）可见，2tσ取决于盾构掘进速度和停机时间。

一般情况下，Wshield>Wlining，故2σ >3σ ，相对于3σ 应力状态，2σ 应力状态相当于对盾构底部土体施加附加荷载Wload：

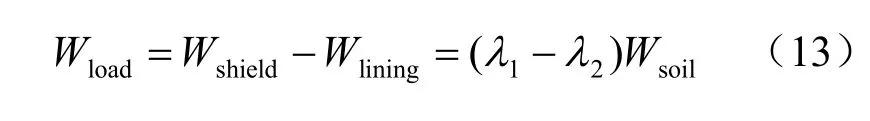
假定Wload均匀作用于盾构机在其底面投影面上，如图6 所示。

图中，Pload=Wload/(LD3)。盾构沿隧道轴线方向掘进，图中矩形分布荷载以速度v 沿盾构前进方向移动。对于任一X 断面盾构底面土体附加应力及沉降的计算，考虑到图中矩形荷载将移动通过X 断面前后，掘进速度均衡的情况下，各个断面先后经历的应力状态基本相同，因此，可将图6 所示计算模型进行简化，将矩形均布荷载转化为条形均布荷载。转化后计算模型如图7 所示。

Mindlin[13]给出竖向点荷载作用在弹性半无限空间内部时的应力弹性解；在Mindlin 解基础之上，Skopek[14]和Poulos 等[15]推导得到条形均布荷载作用在弹性半无限空间内部时竖向应力的弹性解，见式（14），其计算模型见图8。

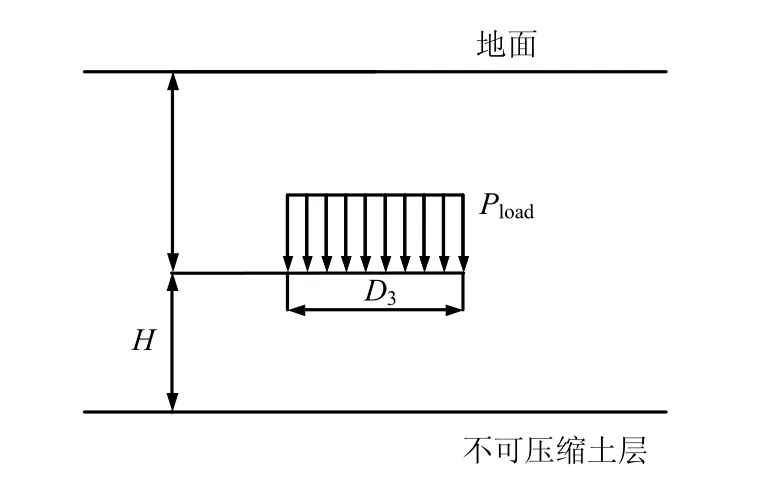
图7 盾构机底面土体附加荷载示意图（简化后） Fig.7 Additional loads imposed on soils beneath the shield（simplified）

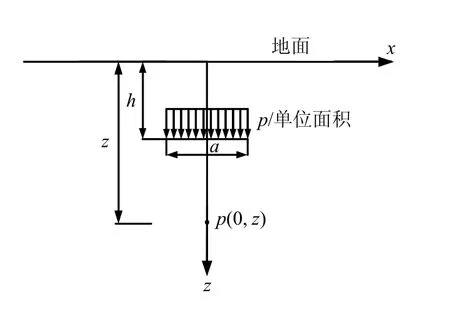
图8 弹性半无限空间内部作用条形荷载 Fig.8 Strip load inside a semi-infinite mass

当x =0时

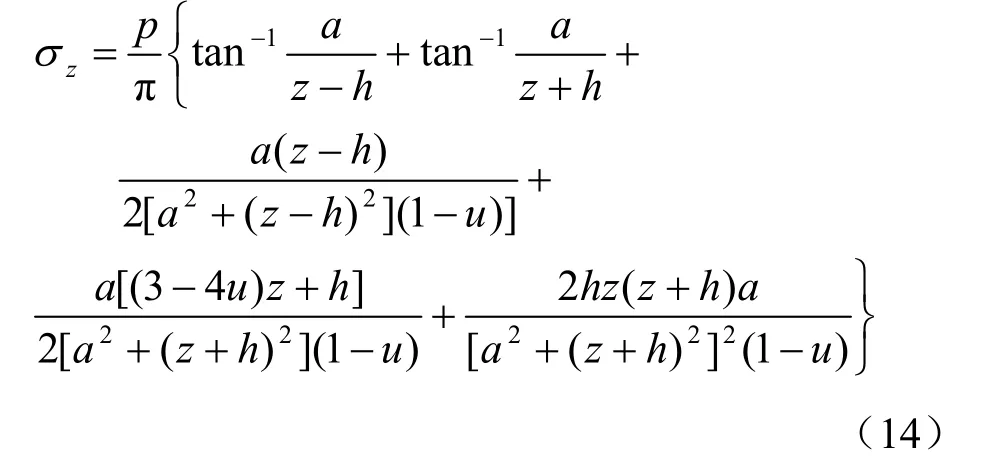
式中：u 为土体泊松比；zσ 为图中P 点竖向附加应力。

将图7 所示计算模型代入式（14），即可得盾构下卧土体轴线位置深度z 处竖向附加应力 σz。

计算得出盾构下卧土层 σ2状态相对于 σ3状态的附加应力之后，在获取计算范围内土体的初始孔隙比、压缩系数等参数后，采用单向压缩分层总和 法[16]即可算得盾构下卧土体因盾构产生的附加应力压缩下卧土层产生的总固结沉降Sc。

在盾构产生的附加应力作用下，其下卧土体排水固结，引述太沙基一维固结理论[16－17]：

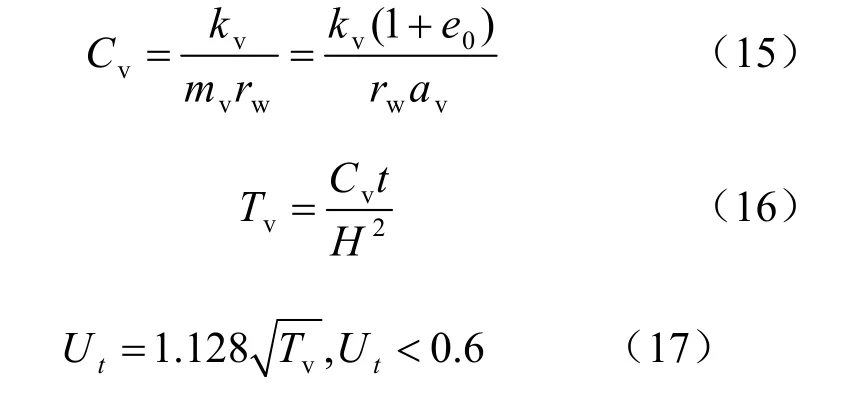
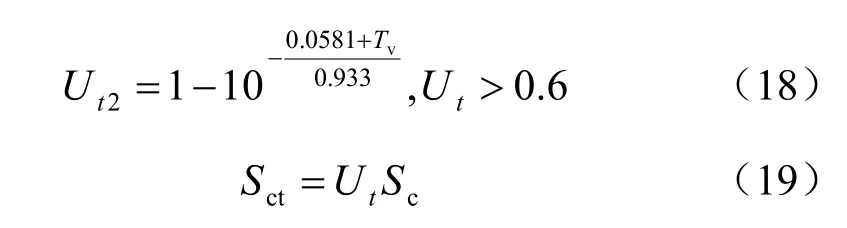
式中：Cv为固结系数（m2/s）；kv为竖向渗透系数（m/s）；mv为体积压缩系数（kPa-1）；rw为水的重度（kN/m3）；av为竖向压缩系数（kPa-1）；e0为土体初始孔隙比；Tv为竖向固结时间因子，无量纲；t 为固结沉降历时（s）；H 为地基土层的最大竖向排水距离（m），对于双面排水为土层厚度的一半，单面排水为土层厚度；Ut为t 时刻平均固结度；Sct为地基t 时刻的主固结沉降（mm）；Sc为地基的总固结沉降（mm）。

获得盾构下卧土层的初始孔隙比、渗透系数、压缩系数等参数后，代入式（15）～（19），即可得到任意时刻t 的固结沉降。

式（11）给出了盾构产生的附加荷载对下卧土层的作用时间，与式（15）～（19）联立，则可算得相对于3σ 状态，在盾构产生的附加应力作用下其下卧土层产生的固结沉降Sct。

3.2 地面沉降计算

盾构机作为一个刚性体，认为其整体位移Sshield与其下卧土层固结沉降相等，即Sshield=Sct。

笔者认为，盾构机下卧土层固结沉降将引起盾构机整体下沉，从而在盾构机顶部与其上部土层之间产生空隙，周围土层填充该空隙引起地面沉降。计算模型如图9 所示。

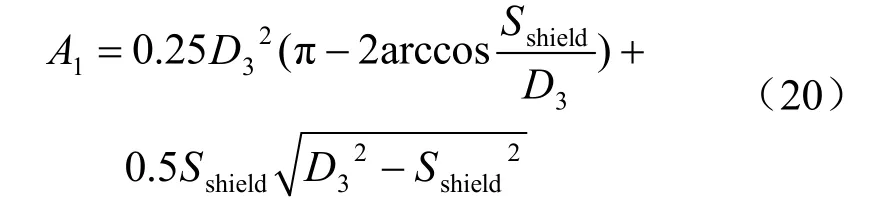
由盾构机位移产生的额外地层损失Vl-a：

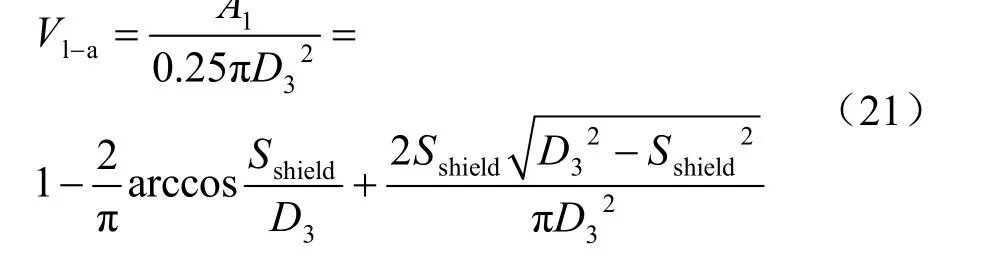
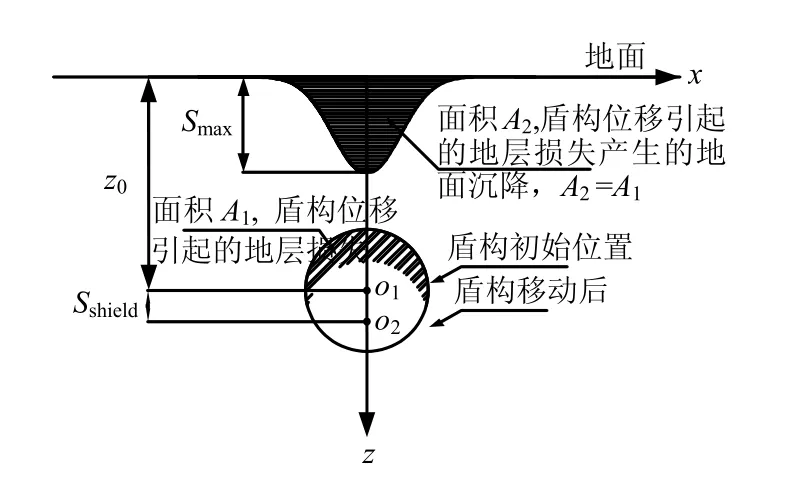
图9 盾构机位移引起的地面沉降计算模型 Fig.9 Calculation model of ground surface settlements due to the shield’s movement

由地层损失引起的地面沉降，本文应用Peck公式[1,18]计算：

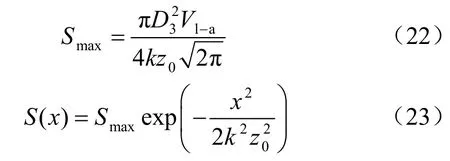
式中：S(x)为地面距离轴线x处地面沉降（mm）；x为距隧道轴线水平距离（m）；Smax为隧道轴线位置地面沉降（mm）；k为沉降槽宽度参数，无量纲。

求得盾构位移Sshield后，代入式（20）～（23），即可求得由于盾构机整体位移引起的地面沉降。

3.3盾构掘进速度及停机时间与地面沉降关系

（1）引入Mindlin解计算盾构下卧土层2σ状态相对于3σ状态的附加应力作用下引起的固结沉降，固结时间由盾构掘进速度及停机时间确定；

（2）盾构整体位移与其下卧土层固结沉降相等，联立式（20）～（23），计算盾构位移引起的地面沉降。

通过以上2步，可以建立盾构掘进速度及停机时间与地面沉降的联系。

4工程实例分析

4.1工程概况及地质条件

杭州市庆春路过江隧道是浙江省重点建设工程，已于2010年12月28日建成通车。该隧道南北方向垂直穿越钱塘江，盾构段总长为3532.442m，其中东线长为1765.478m，西线长为1766.924m。管片外径为11.3m，内径为10.3m，厚为50cm，环宽为2m。管片采用通用契型环，采用6标准块+2邻接块+1封顶块的分块形式，错缝拼装，纵环向采用高强螺栓连接。

盾构隧道采用2台泥水平衡盾构机掘进，2台盾构机均从江南盾构工作井始发，始发段纵向坡度为-4.25%。盾构主机长为10.8m，总重为1170t，外径为11.65m；盾尾后连接3节拖车，上载砂浆泵、电器液压设备、主控室等，长约20m，重约2000t。

沿线场地地貌主要为钱塘江河床及两岸的钱塘江河口冲海积平原，钱塘江南北两岸已建成标准堤塘，岸区已不受潮汐影响，地貌上属平原。拟建隧道与钱塘江垂直，该段河面宽度约为1200m，岸区标高为5.0～6.5m（85国家高程），北岸为钱江新城，已建成庆春路，道路两侧以绿化带为主；南岸以苗木、鱼塘为主，因人工鱼塘开挖影响，微地貌有一定起伏。

盾构施工主要穿越③层粉砂夹粉土、④层淤泥质粉质黏土、⑤层粉质黏土、⑥层粉质黏土、⑦层粉细砂和⑧层圆砾。各土层物理力学指标见表1。

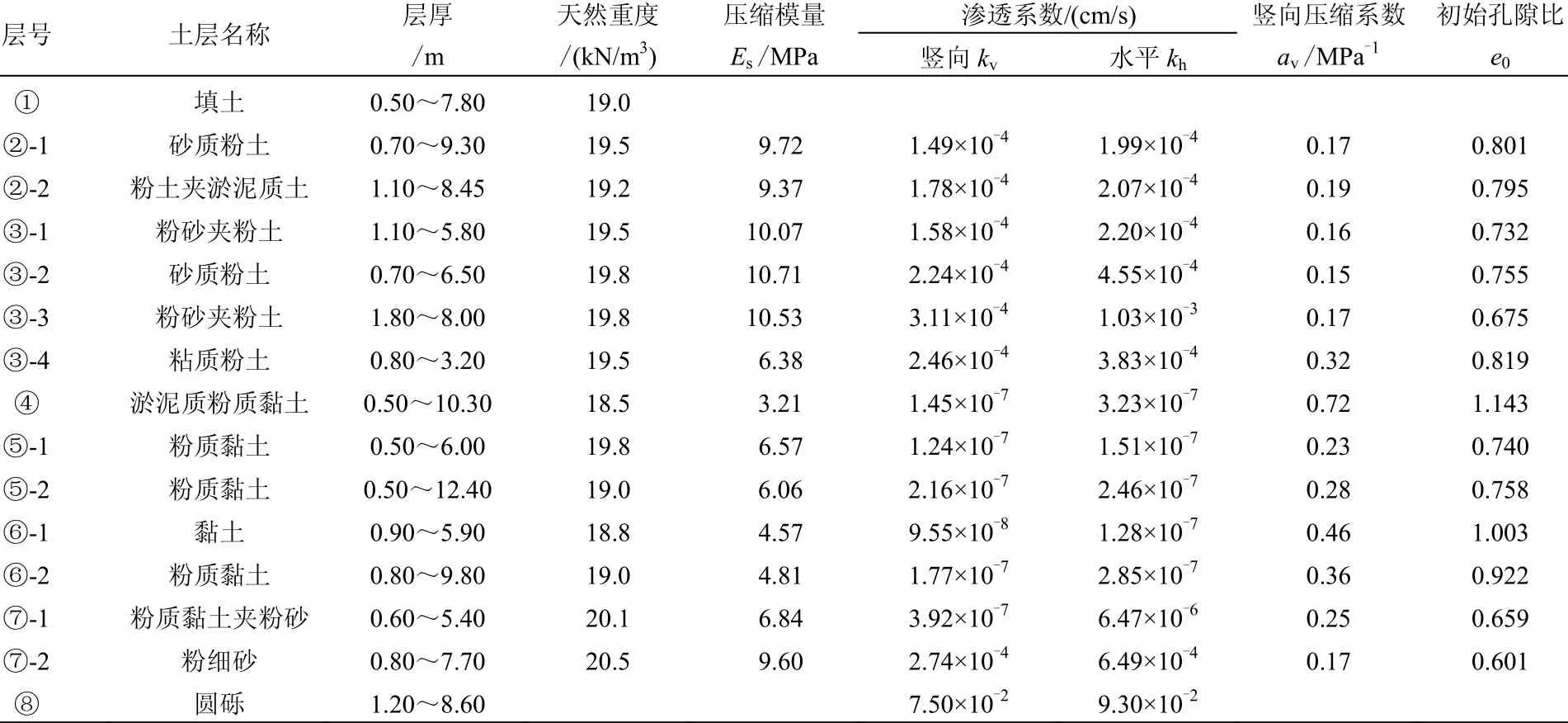
表1场地主要土层物理力学指标Table 1 Soil stratification and physico-mechanical properties

4.2盾构隧道施工引起的地面沉降

东西两线隧道盾构均从江南工作井出发，穿越钱塘江南岸大堤进入钱塘江底。为控制地面沉降和优化盾构掘进参数控制，在江南工作井和大堤之间地面垂直于隧道轴线方向设置了15个地面沉降监测断面，编号S1～S15。以示区分，西线监测断面记为SW，东线记为SE。监测断面布置如图10所示。

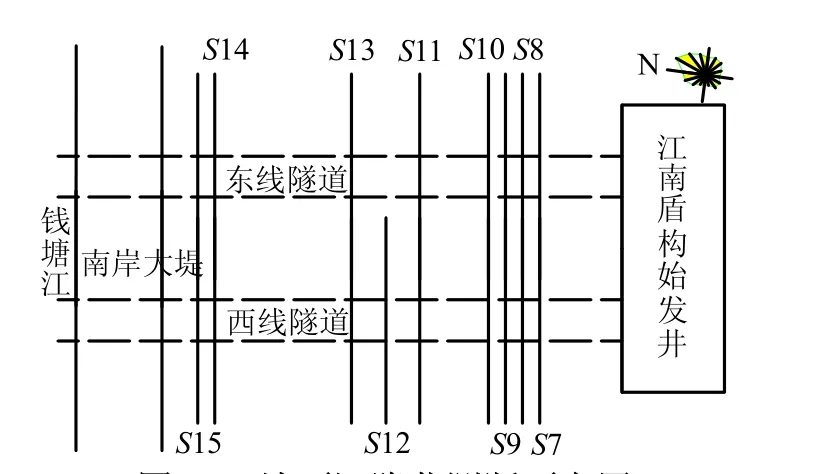
图10 地面沉降监测断面布置 Fig.10 Layout of surface settlements monitoring sections

S1～S6 监测断面处于工作井加固区，地层经加固处理，其沉降已不能反映原状土体位移受盾构施工的影响，故未加以分析。S7～S15 断面隧道施工之前为农田，未曾有施工扰动。

图11 为两线盾构穿越监测断面期间掘进进度曲线。图中虚线自下而上依次代表S7～S15 断面所处里程。

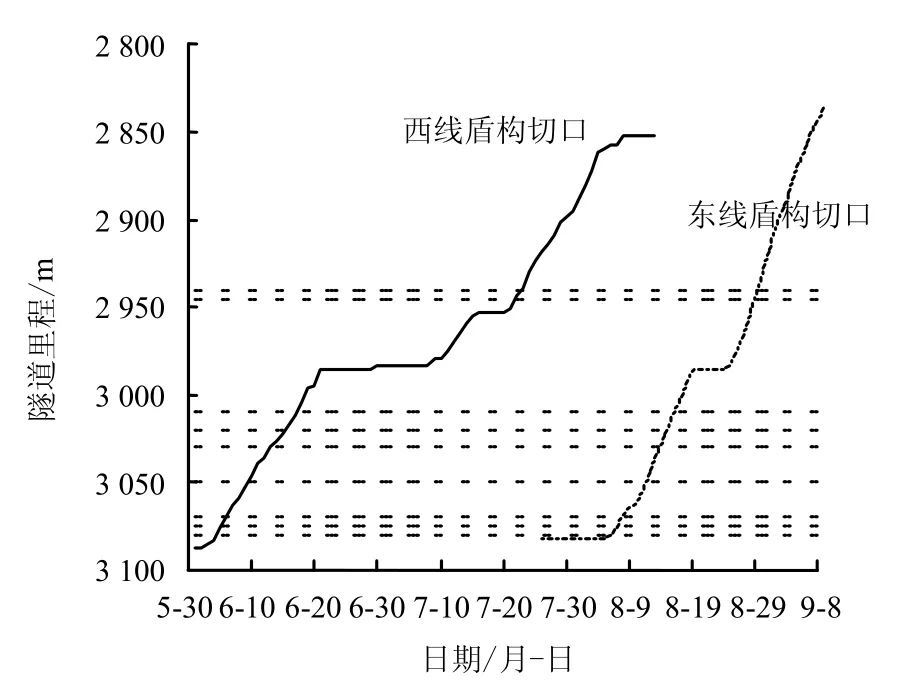
图11 盾构掘进进度曲线 Fig.11 Advance-time curves of shield machines

由图11 可见，两线盾构穿越监测断面期间掘进速度较均匀，西线盾构非正常停机2 次，东线1 次。若不计停机时间，东西线盾构平均掘进速度分别为8.59 m/d 和5.74 m/d。

图12 为西线各监测断面隧道轴线位置地面沉降随盾尾离开时间的变化曲线。S14、S15 断面靠近钱塘江南岸大堤堤脚，其地面沉降受大堤影响较大，与之前断面地面沉降差别较大，未加以分析。t 为盾构盾尾离开监测断面时间（d），正值表示盾尾已经脱离监测断面，而负值表示盾尾尚未到达监测断面；S 为地面位移值，地面隆起记为正值，地面沉降记为负值（mm）。

由图12 可见，SW7～SW11 沉降规律基本一致：在盾尾脱离约10 d之后，各断面沉降曲线基本平行，表明各断面地面沉降速率基本相同，此时地面沉降主要为扰动土体固结引起，可见SW7～SW11 地面固结沉降速率基本一致。

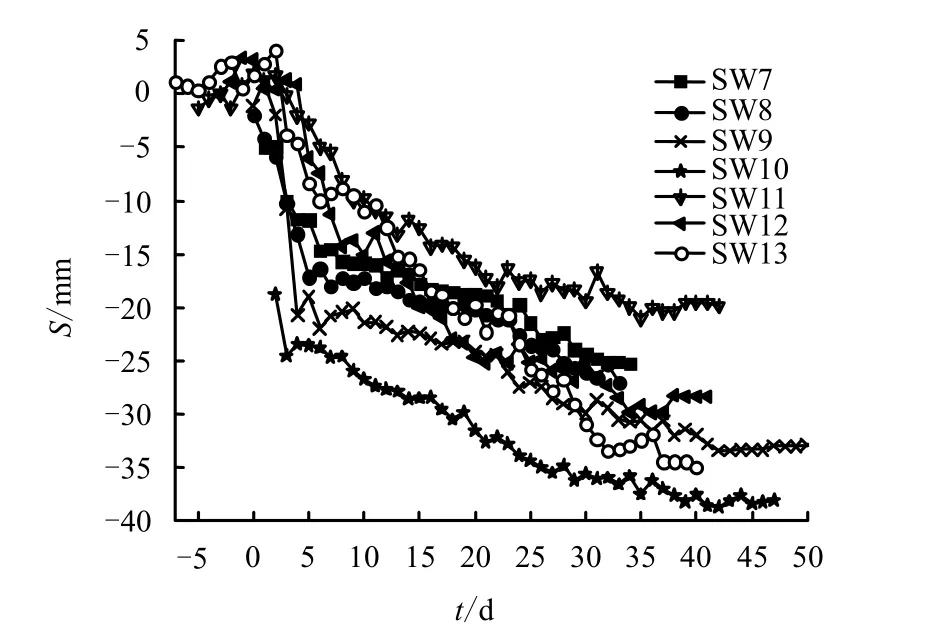
图12 西线隧道轴线地面沉降随盾尾离开时间变化曲线 Fig.12 Settlement-time curves of ground surface of west axis

而SW12 和SW13 沉降曲线与SW7～SW11 差别较大：t =10～23 d 期间，SW12 和SW13 沉降曲线基本平行，其斜率明显大于SW7～SW11 沉降曲线；23 d 之后，SW12 沉降曲线与SW7～SW11 基本平行，而SW13 沉降曲线斜率还是明显大于其他断面。

如图11 所示，西线盾构切口穿越SW12、SW13后停机长达18 d，此时，盾构拖车刚好位于SW13断面正下方，拖车尾部离开SW12 断面约2.9 m。

图13 为东线各监测断面隧道轴线位置地面沉降随盾尾离开时间的变化曲线。同样，S14、S15 断面未加以分析。

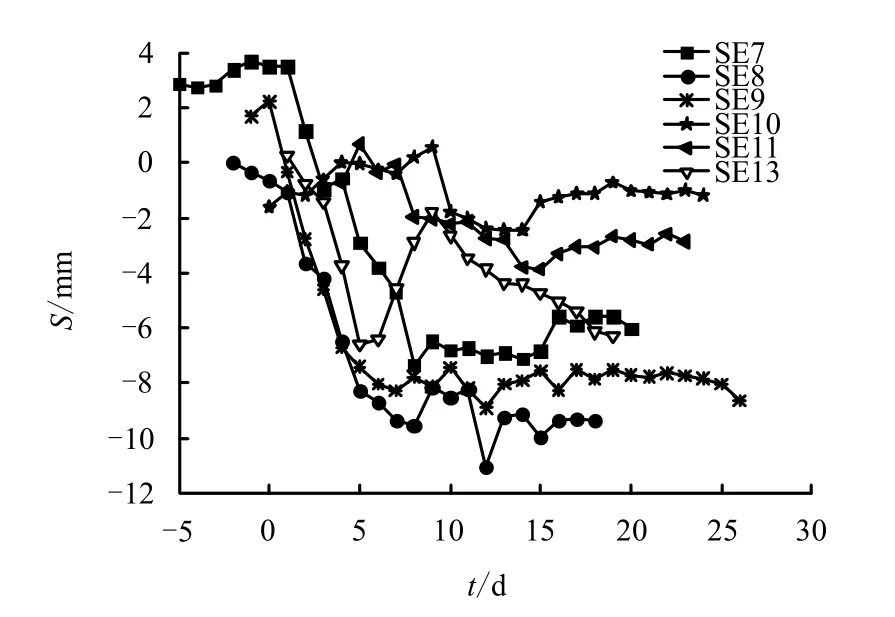
图13 东线隧道轴线地面沉降随盾尾离开时间变化曲线 Fig.13 Settlement-time curves of ground surface of east axis

由图13 可见，盾尾脱离0～9 d 期间，各断面沉降规律差别较大，主要受盾尾同步注浆控制差异所致；SE7～SE9 在盾尾脱离约8 d 之后地面沉降趋于稳定；SE10、SE11 在盾尾脱离约14 d 之后地面沉降趋于稳定；而SE13 断面在盾尾脱离约19 d 时，地面仍保持较大的沉降速度。盾尾脱离约9 d 之后，SE13 沉降曲线斜率明显大于其他断面，反应了其固结沉降速度远大于其他断面。

由图11 可见，东线盾构切口离开SE13 断面23.85 m 后，由于设备故障停机7 d，此时盾构拖车刚好位于SE13 正下方。

4.3 理论验证

由以上分析可见，盾构长时间停机后，所在断面地面固结沉降速度往往大于其他断面。现选取SW13 断面，采用前面所述方法，建立盾构掘进速度及停机时间与地面沉降的联系。

SW13 剖面如图14 所示。

图14 SW13 地质剖面及土中应力计算 Fig.14 Geological profile of monitoring section SW13 and calculation results of soil stresses

4.3.1 土中有效应力计算

计算参数选取：z0=23.26 m，D1=11.3 m，D2= 10.3 m，D3=11.65 m，L =30.8 m，Wshield=34 006 kN（盾构主机与后续拖车重量之和，并考虑到管片运输行车、拖车长度范围内拼装完成管片重量、砂浆运输行车及施工班组等产生的额外压重300 t），h = 0.8 m，H = 7.525 m，各土层土体重度见表1，rlining= 25 kN/m3，rgrout=20 kN/m3，rw=9.8 kN/m3，土体泊松比u =0.45，依照施工经验，取k =0.25。

图中各个阶段应力状态计算结果见图14。盾构底部土体有效应力状态3 及盾构压重相对于应力状态3 在土体内部的附加应力详见图15。

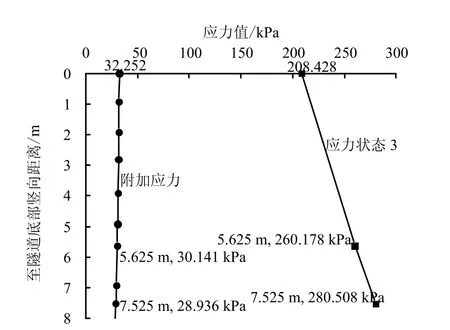
图15 盾构机底部土体应力状态3 及附加应力 Fig.15 Stress conditions 3 and additional stress in soils beneath the shield

4.3.2 固结沉降计算

（1）总固结沉降量计算

采用单向压缩分层总和法[16]计算盾构底部土体固结沉降Sc。图15 可见，盾构底部土层中附加应力曲线可近似以直线取代，故可取各土层中间位置附加应力值进行计算。

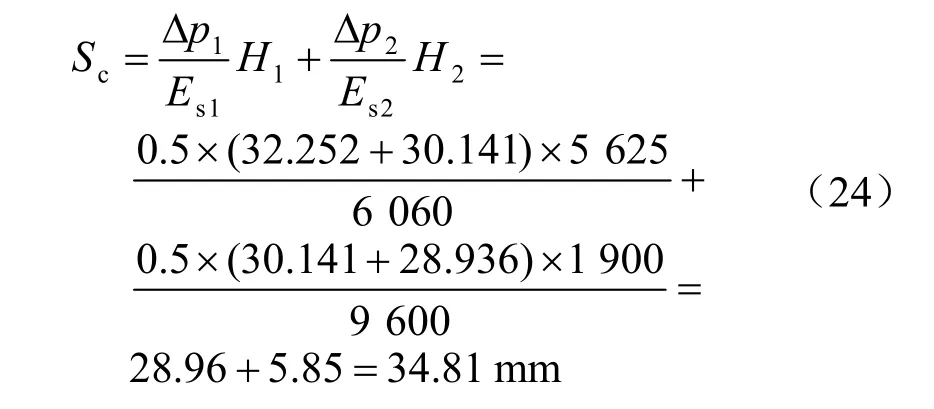
式中：Δp1、Δp2分别为盾构机底部⑤-2 粉质黏土层和⑦-2 粉细砂层中间位置附加应力值（kPa）；Es1、Es2分别为⑤-2 粉质黏土层及⑦-2 粉细砂层压缩模量，取值见表1（kPa）；H1、H2分别为盾构机底部⑤-2 粉质黏土层及⑦-2 粉细砂层厚度（m）。

由式（24）计算可得，盾构下卧土体，⑤-2 粉质黏土层总固结沉降Sc1=28.96 mm，⑦-2 粉细砂层总固结沉降Sc2=5.85 mm。

（2）平均固结度的计算

国内外众多工程实例表明，采用太沙基一维固结理论[16－17]计算所得固结沉降速率较实测值明显要小，这主要因为太沙基一维固结理论仅考虑了孔隙水压力的竖向消散，而实际问题中水平向的排水加速了超静水压力的消散[19－22]。

由表1 可见，本工程盾构穿越各土层水平向渗透系数kh远大于竖向渗透系数kv，若采用仅考虑竖向渗流的太沙基一维固结理论计算固结度，计算结果将较实际情况偏小。

盾构匀速掘进时，盾构对其下卧土层的附加荷载可简化为条形均布荷载；而盾构停机时，可简化为矩形均布荷载，若仍按条形均布荷载计算，结果偏保守；而本文以盾构下方轴线位置的附加应力进行固结沉降计算，最终固结沉降量也偏大。考虑到采用一维固结理论计算固结度结果偏小，可与最终沉降量偏大的计算结果部分抵消，且一维固结理论较二维、三维固结问题简单，便于工程应用，故本文仍采用太沙基一维固结理论计算盾构下卧土层固结度。

盾构底部有2 层土体，代入式（15）～（19），分别计算各土层的固结沉降，假定单面排水。计算参数取值见表1。计算结果如下：

⑤-2 粉质黏土层

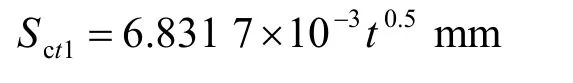
⑦-2 粉细砂层

Ut2=0.99 时，t =2 441.728 s=0.678 3 h 可见，盾构底部⑦-2 粉细砂层孔隙水压力消散较快，可认为其瞬时完成压缩沉降，盾构掘进速度快慢及停机时间对该土层沉降不会产生影响。

综上所述，

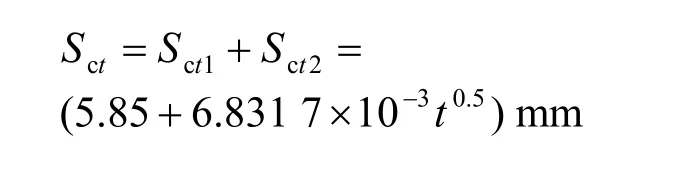
4.3.3 地面沉降计算

应用式（20）～（23）建立盾构下卧土体固结沉降与其引起的地面沉降的关系。计算结果见图16、17。

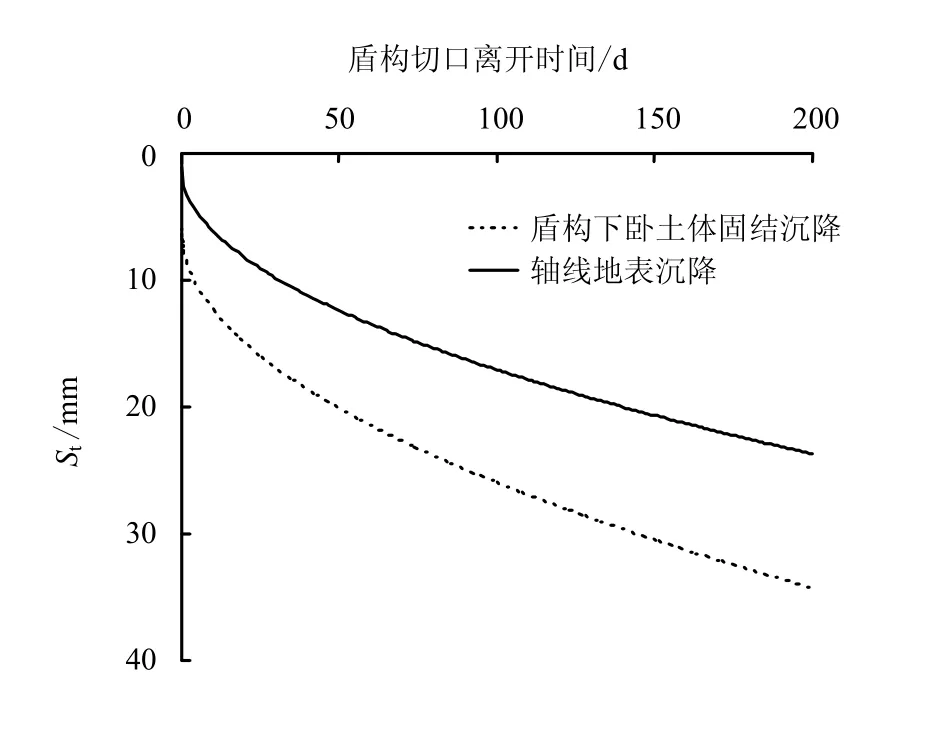
图16 SW13 断面盾构底部土体固结沉降及轴线地面沉降 Fig.16 Settlements-time curves of soils beneath the shield machine and ground surface above centerline of the tunnel

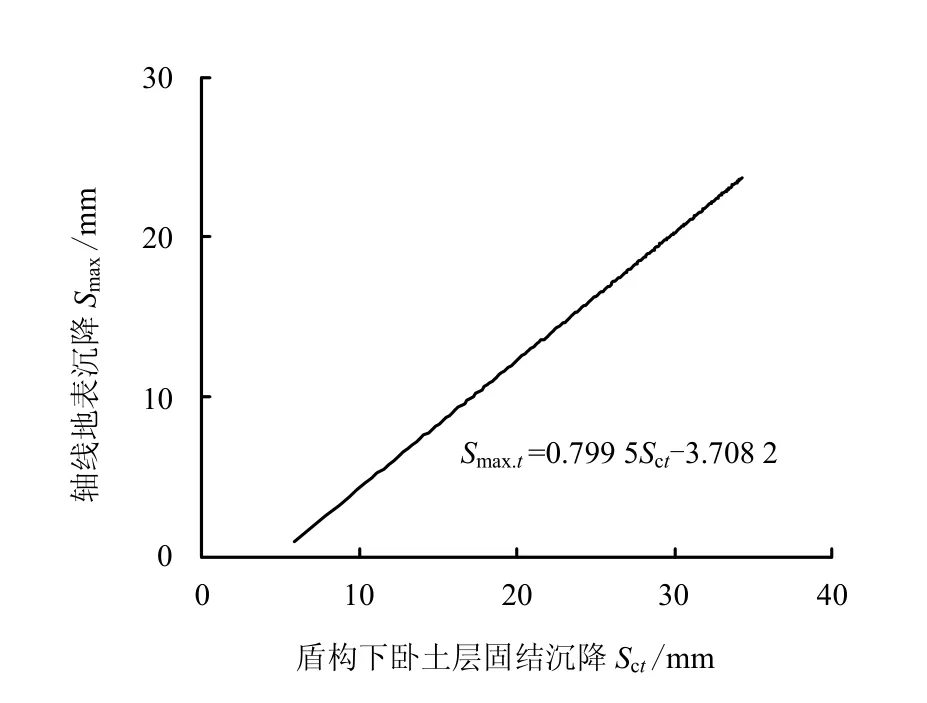
图17 Smax.t 与Sct 关系曲线 Fig.17 Relation between Smax.t and Sct

由图17 可见，轴线地面沉降Smax.t和盾构下卧土层沉降Sct近似呈线性关系：

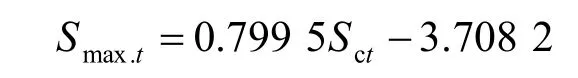
4.3.4 地面沉降比较

（1）西线地面沉降

西线盾构下卧土层受盾构压重影响时间 2tσ：

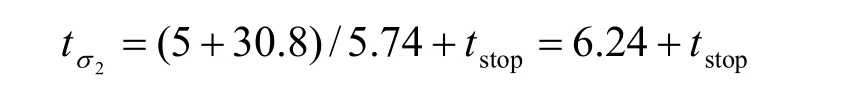
盾构主机长为10.8 m，盾构切口到达某断面至盾尾离开的时间约为1.88 d，故以盾尾离开监测断面时间表示，盾构压重在各监测断面影响时间为[-1.88 d，4.36 d+tstop]。

盾构盾尾离开SW13 断面2 d 后，因设备故障停机18 d，之后恢复正常掘进。

SW13 盾构压缩下卧土层时间为24.24 d，时间段为[-1.88 d，22.36 d]，SW12 断面盾构压缩下卧土层时间段为[-1.88 d，22.36 d]，其他断面盾构压缩下卧土层时间段为[-1.88 d，4.36 d]。

t =[-1.88 d，4.36 d]，各监测断面盾构下卧土层均受到盾构产生的附加应力的影响，随后[4.36 d，22.36 d]期间，仅SW12、SW13 还受其影响。

由于各监测断面地质剖面及隧道埋深不尽相同，因此，盾构下卧土层固结沉降及固结沉降与地面沉降的关系不尽相同。考虑到各监测断面相离较近，土层及隧道埋深情况基本一致，近似用图16曲线计算其他断面盾构压缩下卧土层固结沉降及引起的地面沉降。

图18 为各断面沉降比较。图中，Sstop为计算所得由盾构停机引起的地面沉降，SW12-Sstop、SW13-Sstop分别为SW12 和SW13 地面实测沉降与由盾构停机引起的地面沉降之差。

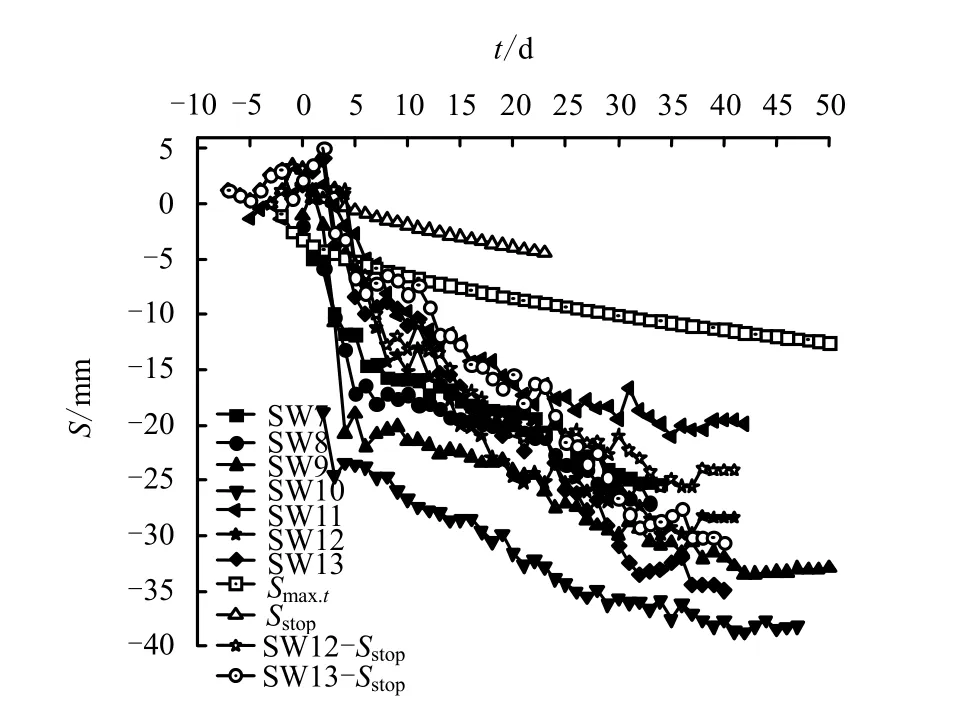
图18 西线各断面沉降情况 Fig.18 Ground settlements of monitoring sections for west route

由图18 可见，去除盾构停机引起的地面沉降之后，SW12 断面沉降与其他断面沉降规律基本相同。而SW13 断面，去除盾构停机引起的地面沉降之后，在停机时间段内（t=[4.36 d，22.36 d]）的地面沉降规律与其他断面基本一致，而随后监测时间内的地面沉降速度还是较其他断面要大。

造成以上差别的原因，笔者认为，由于盾构机停机时产生较大沉降，再次掘进时姿态较难控制，由于拖车尾部已经离开SW12 断面约2.9 m，掘进不会对SW12 产生显著扰动；而SW13 断面刚好位于拖车中部，对其扰动较大，这是图18 所示SW13断面地面沉降虽已不受盾构压重影响但仍保持较大沉降速度的原因。

（2）东线地面沉降

东线盾构下卧土层受盾构压重影响时间 1tσ：

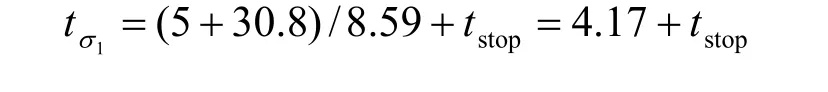
盾构机切口到达某断面至盾尾离开的时间约为1.26 d，故以盾尾离开监测断面时间表示，盾构压重在各监测断面影响时间为[-1.26 d，2.91 d+tstop]。

盾尾离开SE13 断面约13.05 m 后（拖车刚好位于SE13 正下方），因设备故障停机7 d，之后恢复正常掘进。

SE13 断面盾构压缩下卧土层时间为11.17 d，时间段为[-1.26 d，9.91 d]，其他断面盾构压缩下卧土层时间段为[-1.26 d，2.91 d]。

SE13 断面地质情况及隧道埋深与SW13 基本一致，因此，可近似使用图16 结果。对于其他断面，盾构压缩下卧土层引起的地面沉降仍近似用图16曲线表示。

图19 为各断面沉降比较。

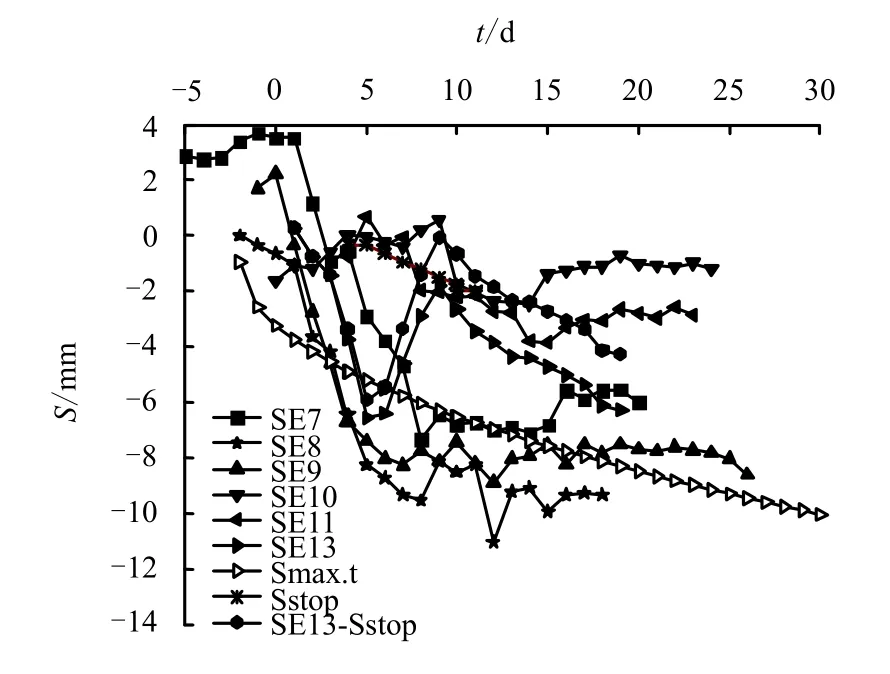
图19 东线各断面沉降情况 Fig.19 Ground settlements of monitoring sections for east route

由图可见，扣除时间段[2.91 d，9.91 d]内由盾构停机引起的地面沉降之后，在该时间段内SE13断面沉降规律与其他断面仍不一致。究其原因，主要为该段时间盾尾注浆差异引起的。SE8 和SE9 断面该时间段内地面持续沉降，而SE10、SE11 断面则发生隆起，SE13 断面先是持续沉降后又较大隆起。由于盾尾注浆压力作用差异，各个监测断面总沉降在时间段[0，10 d]差异较大，所以SE13 扣除盾构停机引起的地面沉降后，其沉降规律在该时间段内与其他断面仍不同。

盾尾脱离10 d 之后，SE13 已不受盾构附加荷载影响，但其地面沉降速度仍较其他断面要大，而其他断面较一致。该差别主要为盾构恢复掘进时对SE13 断面的施工扰动所致。

（3）两线地面沉降

综上可见，西线盾构各监测断面地面沉降受盾尾同步注浆引起的差异较小，总沉降规律基本相同，扣除盾构停机影响后，本文所述理论较好地解释了盾构停机期间地面沉降较大的原因，盾构下卧土层固结沉降及其引起的地面沉降计算理论基本正确。

东线盾构各监测断面地面沉降受盾尾同步注浆引起的差异较大，总沉降规律在盾尾刚脱离初期(0～10 d)差别较大，所以扣除盾构停机影响后，各断面沉降规律仍难一致。

两线隧道地面沉降可以看出，盾构长时间在某一断面搁置时，由于压缩下卧土层引起盾构整体下沉，在恢复掘进时，盾构姿态较难控制，会引起较大施工扰动，加剧地面沉降。

5 结 论

（1）引入Mindlin 解计算盾构压重在其下卧土层产生的附加应力，采用单向分层总和法计算下卧土层总固结沉降，使用太沙基一维固结理论计算盾构压重影响时间内的沉降量，并用Peck 公式建立起该固结沉降与地面沉降的联系。杭州庆春路越江隧道地面沉降的实测数据验证表明，上述理论基本可以建立盾构掘进速度与停机时间和盾构压缩下卧土层引起的地面沉降的联系。

（2）当盾构下卧土层为黏性土，黏土层下卧砂土或圆砾等透水层时，盾构压重引起的地面沉降较大。盾构下卧土层的固结沉降和其引起的地面沉降基本呈线性。

（3）盾构附加荷载在其下卧土层的作用时间取决于盾构掘进速度和停机时间；掘进速度越快，正常停机或非正常停机时间越短，盾构附加应力作用下其下卧土层固结沉降越小，进而其引起的地面沉降越小。因此，在其他掘进参数控制一致的前提下，提高掘进速度，避免非正常停机或降低停机时间，有利于减少盾构施工引起的地面沉降。

（4）盾构长时间停机后整体下沉，恢复掘进时，姿态较难控制，会加大地层扰动，加剧地面沉降。

本文在建立计算模型时，应用了许多假定，附加应力、固结沉降及固结度的计算受计算公式和土体参数选取的影响较大，且计算结果仅在本工程中得到验证。因此，对于本文理论的普遍适用性有待在更多的工程实践中加以验证和改进。

[1] PECK R B. Deep excavations and tunneling in soft ground[C]//Proceedings of 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City: Thomas Telford, 1969: 225－290.

[2] YOSHIKOSHI WATARU, WATANABE OSAMU, TAKAGI NOBUO. Prediction of ground settlements associated with shield tunnelling[J]. Soils and Foundations, 1978, 18(4): 47－59.

[3] 朱才辉, 李宁, 柳厚祥, 等. 盾构施工工艺诱发地表沉降规律浅析[J]. 岩土力学, 2011, 32(1): 158－164. ZHU Cai-hui, LI Ning, LIU Hou-xiang, et al. Analysis of ground settlement induced by workmanship of shield tunnelling[J]. Rock and Soil Mechanics, 2011, 32(1): 158－164.

[4] LEE K M, ROWE R KERRY, LO K Y. Subsidence owing to tunneling. I. Estimating the gap parameter[J]. Canadian Geotechnical Journal, 1992, 29: 929－940.

[5] ROWE R KERRY, LEE K M. Subsidence owing to tunneling. II. Evaluation of a prediction technique[J]. Canadian Geotechnical Journal, 1992, 29: 941－954.

[6] ROWE R KERRY, LEE K M. Subsidence owing to tunneling. II. Evaluation of a prediction technique:1Reply[J]. Canadian Geotechnical Journal, 1994, 31: 467－469.

[7] PARK K H. Elastic solution for tunnelling-induced ground movements in clays[J]. International Journal of Gemechanics, 2004, 4(4): 310－318.

[8] WEI-I CHOU, ANTONIO BOBET. Predictions of ground deformations in shallow tunnels in clay[J]. Tunnelling and Underground Space Technology, 2002, 17(1): 3－19.

[9] NOMOTO TOSHI, IMAMURA SHINICHIRO, HAGIWARA TOSHIYUKI, et al. Shield tunnel construction centrifuge[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(4): 289－300.

[10] FINNO RICHARD J, CLOUGH G WAYNE. Evaluation of soil response to EPB shield tunneling[J]. Journal of Geotechnical Engineering, 1985, 111(2): 155－173.

[11] CLOUGH G WAYNE, SWEENEY BRYAN P, FINNO RICHARD J. Measured soil response to EPB shield tunneling[J]. Journal of Geotechnical Engineering, 1983, 109(2): 131－149.

[12] VERRUIJT A, STRACK O E. Buoyancy of tunnels in soft soils[J]. Géotechnique, 2008, 58(6): 513－515.

[13] MINDLIN R D. Force at a point in the interior of a semi-infinite solid[J]. Journal of Applied Physics, 1936, 7(5): 195－202.

[14] SKOPEK J. The influence of foundation depth on stress distribution[C]//Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering. Paris: [s. n.], 1961.

[15] POULOS H G, DAVIS E H. Elastic solutions for soil and rock mechanics[M]. New York, London, Sydney, Toronto: John Wiley & Sons, inc., 1974.

[16] 龚晓南. 土力学[M]. 北京: 中国建筑工业出版社, 2002: 99－114.

[17] 龚晓南. 高等土力学[M]. 杭州: 浙江大学出版社, 1996: 92－111.

[18] O’REILLY M P, NEW B M. Settlements above tunnels in the United Kingdom-their magnitude and prediction[C]// Tunneling 82. Papers Presented at the third International Symposium. London: Institution of Mining and Metallurgy, 1982: 173－182.

[19] 李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004.

[20] 顾晓鲁, 钱鸿缙, 刘惠珊, 等. 地基与基础(第三版)[M]. 北京: 中国建筑工业出版社, 2003: 138－198.

[21] CRAWFORD C B. State of the art: evaluation and interpretation of soil consolidation tests[R]// Consolidation of Soils: Testing and Evaluation. Lauderdale: the ASTM Symposium on Consolidation Behavior of Soils, Ft., 1985: 71－101.

[22] DAVIS E H, POULOS H G. The use of elastic theory for settlement prediction under three-dimensional conditions[J]. Géotechnique, 1968, 18(1): 67－91.