一种新型数控可变电感的研究与设计*

刘漫霞，张 辉，陈古典，龚 文

(中山大学智能交通研究中心，广州510006)

近年来，电路系统的数字化控制需求日益增加，因此往往需要电路中的各种原件参数也能够进行数字化调节和控制，数控电阻［1］、数控电容［2］等可以通过数字控制参数的电路元器件应运而生。但是，由于电感换路过程中出现的过压等问题［3］，使得电感量数字可控的电感元件难以实现。

目前，电感元件电感量的改变通常采用机械式调节，其基本方式包括:磁芯可调电感器、铜芯可调电感器、滑动接点可调电感器、串联互感可调电感器和多抽头可调电感器［4-7］等。这些方式很难实现实时在线自动调节，且不能够按照使用者需求来精确定量控制电感值的大小。因此在实际应用中存在很大的局限性。因此，需要设计一种电感量电子可调的结构和方法，才能实现电感量的数字化控制。已有一些学者应用电力电子技术设计，实现电感量的电子调节［8］，但是由于其结构和成本方面的原因，通常应用于电力网络中，并不适合一般电子线路的使用。

为此，本文针对这一问题，应用电感间的互感特性，设计了一种结构简单，适用于一般电子线路的新型数控可变电感，实现了电路中电感量的数字化控制。

1 数控可变电感设计原理

由一般电路知识［3］可知，当两个电感距离比较近，且其中都有电流流过时，两者电磁场会相互影响导致两个电感的特性发生改变，两者之间影响的大小即为两个电感之间的互感。本文设计的可变电感就是应用了这一基本特性。其基本原理如图1所示。

图1中，电感L1即为接入电路的被控制电感称为主电感;电感L2称为附属电感，用于调节和控制，且电感L1和电感L2之间的互感为M。设L1接入电路后两端的电压为ui，流经L2的电流为i1;控制电路按照ui的大小产生一个电压kui加载在附属电感L2两端，流经L2的电流为i2。

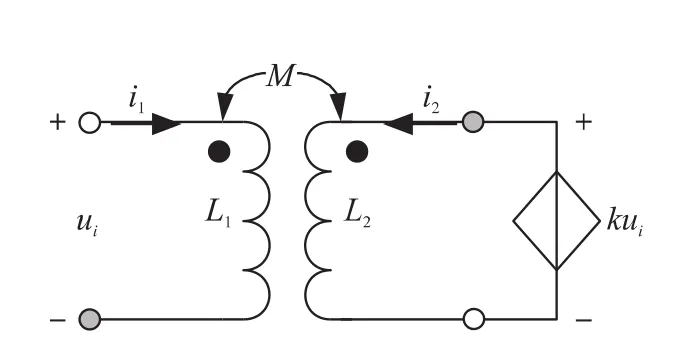
图1 可变电感原理结构图

此时，图1的原理结构图中主电感L1和附属电感L2两个回路中可以推导出以下两个等式:

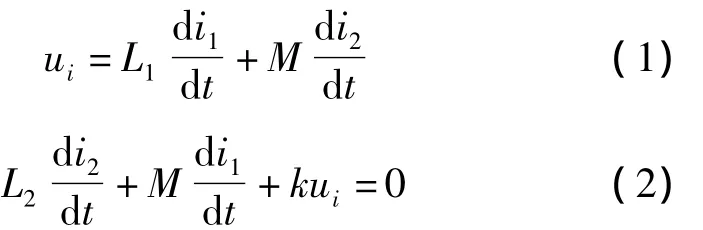
对于正弦交流输入［9］，不考虑瞬态过程［10］的情况下，式(1)和式(2)的稳态表达式为:

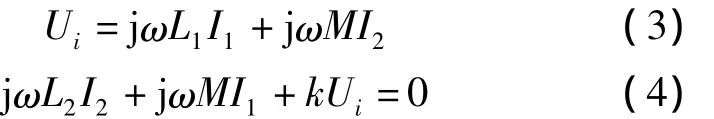
其中，I1是流经电感L1的稳态电流，I2是流经电感L2的稳态电流，Ui是L1接入电路后的稳态电压。

由式(3)、式(4)可得到主电感输入端的等效电抗为:

对比式(5)和一般电感Lx的感抗特性:

其中，UL为电感上交流电压的幅值，IL为电感上交流电流的幅值，可以发现对于主电感输入端，其等效电感为:

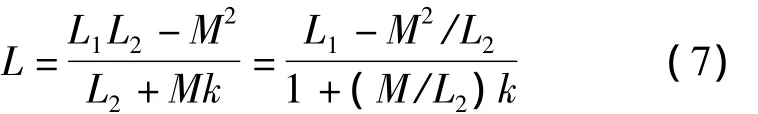
由式(7)可知，L1，L2，M都是定值，等效电感L值的只与放大倍数k值的大小相关。因此可以通过改变k值的大小来调节等效电感L的电感量。

根据以上讨论，只需设计一个数字可控的放大器，对主电感的电压进行k倍的放大作为附属电感的驱动信号，即可实现对电感参数的数字化控制。

2 电感调节控制电路模块设计

为了实现式(7)的电感量控制，本设计如图2所示的数控可变电感电路，其主要包括:主电感L1，附属电感L2，以及控制电路——电压跟随器电路、比例运算电路、数字电位器电路和功率放大电路。

(1)电压跟随器电路一

电压跟随器电路的主要功能是提高输入阻抗，减小对前级电路的负担，在所设计的电路结构中，电压跟随器1主要保证控制电路不对主电感所在的主回路电压电流造成额外干扰;电压跟随器2主要用于减小数字电位器的负载，降低输出电流。这两个跟随器电路可以统一采用运算放大器构成的跟随器(结构如图3所示)，它不仅结构简单，而且输入输出之间没有相位差，不会对式(7)的实现造成不利影响。

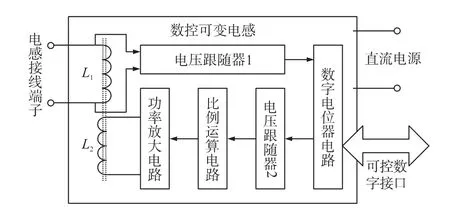
图2 数控可变电感结构示意图

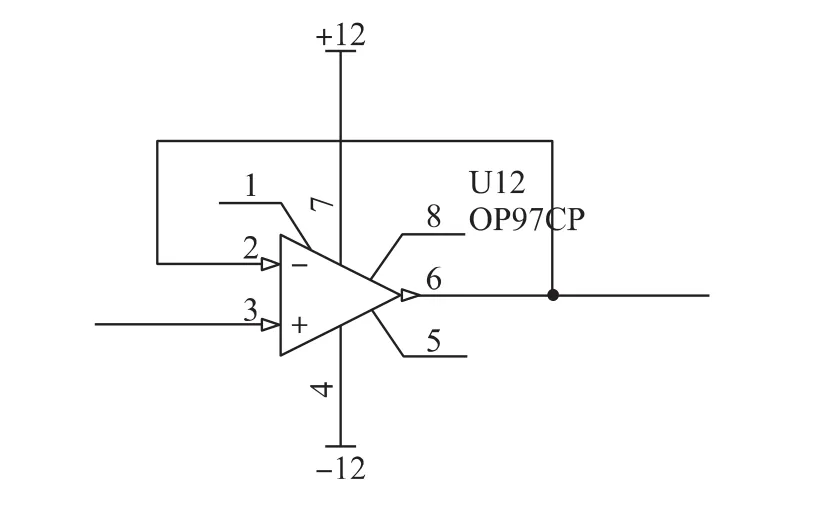
图3 电压跟随器电路

(2)数字电位器电路模块

数控可变电感的核心在于设计数字可控的放大器，根据输入的数字量调节放大系数k以实现电感参数的数字可控。而数字电位器正是这样一种器件，他可以根据输入数字指令准确地进行电阻值调节，从而实现对输入信号的分压。本文采用X9241数字电位器实现这一过程。

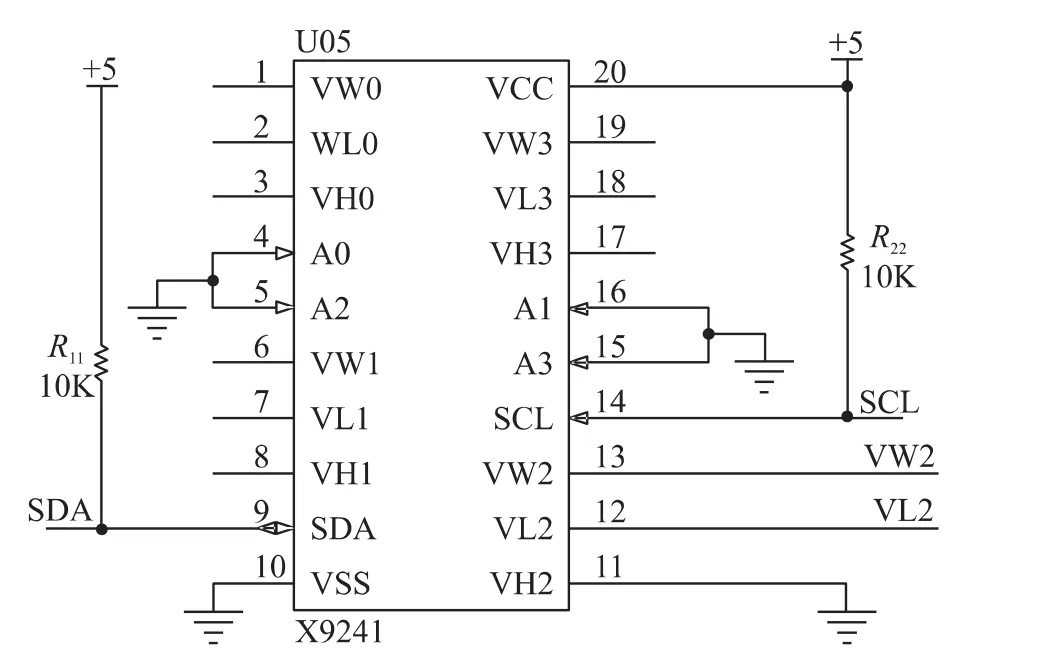
图4 数字电位器X9241电路图

数字电位器X9241的电路图如图4所示，其中，SCL和SDA分别为I2C总线的时钟线和数据线，用于接收外部的数字指令，需要加上拉电阻，起限流和输出高电平的作用［11］。数字电位器X9241里有4个电位器，本电路中使用第3个电位器，即高端、低端和滑动端分别为VH2、VL2和VW2。VL2接经过跟随器隔离的输入信号ui，VH2接地，VW2端则输出经过数字电位器改变的输出信号kui。

外部控制系统通过SDA和SCL给X9241发送数据指令，改变数字电位器滑动计数寄存器(WCR)的数值(最大为63，最小为0)，k1随即发生变化，其具体表达式可以表示为:

因此0≤k1≤1。例如，当滑动端的数据内容为10时，k1=10/63。

(3)比例运算电路

由于数字电位器只能实现分压的功能，即它的调节系数0≤k1≤1，数值范围过小，往往难以满足实际需要，为此加入比例运算环节，将数字电位器的输出信号进行k2倍放大，进而得到附属电感上的加载电压值kui=k1k2ui。其中k2可以通过同相比例运算电路实现，结构如图5所示。同相比例运算电路中，输出电压与输入电压成正比关系，且二者相位相同［11］，放大系数k2为:

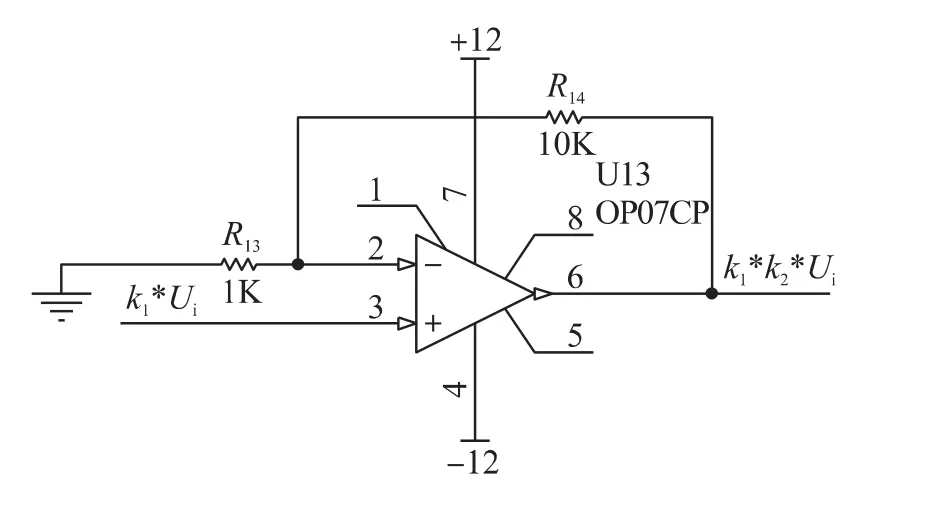
图5 同相比例运算电路

(4)功率放大电路

通过数字电位器和比例运算电路初步的确定了一个变化系数k值之后，需要功率放大电路来放大电路的输出功率，从而推动电感L2工作，使其与电感L1产生互感效应，最终实现可变电感的数字可控。

功率放大电路采用的无输出电容的功率放大电路(OCL电路)，如图6所示。这一电路不对输入信号的电压幅度进行放大(即放大系数为1)，只提高电流的输出能力用以驱动较重的负荷。其特点是结构简单，输入输出之间没有相位差。

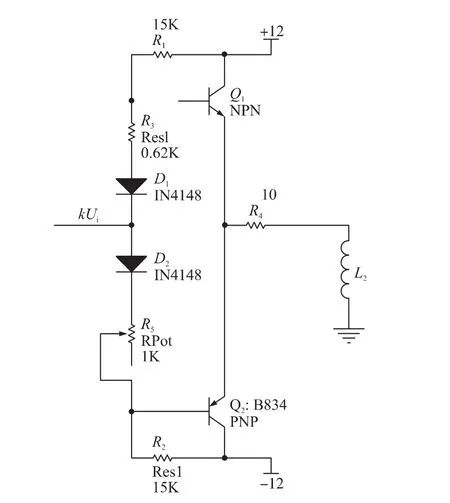
图6 功率放大电路

3 实验测试结果与分析

为了验证电路的有效性，应用第2节所述电路进行实验测试，在L1=L2=65 μH，k2=10的条件下，调节WCR值，通过谐振频率法测得对应的电感值如表1所示。从表1中可见，电感值与WCR的数值呈反比，即电感值随着k值的增大而减小，与式(7)的规律一致。

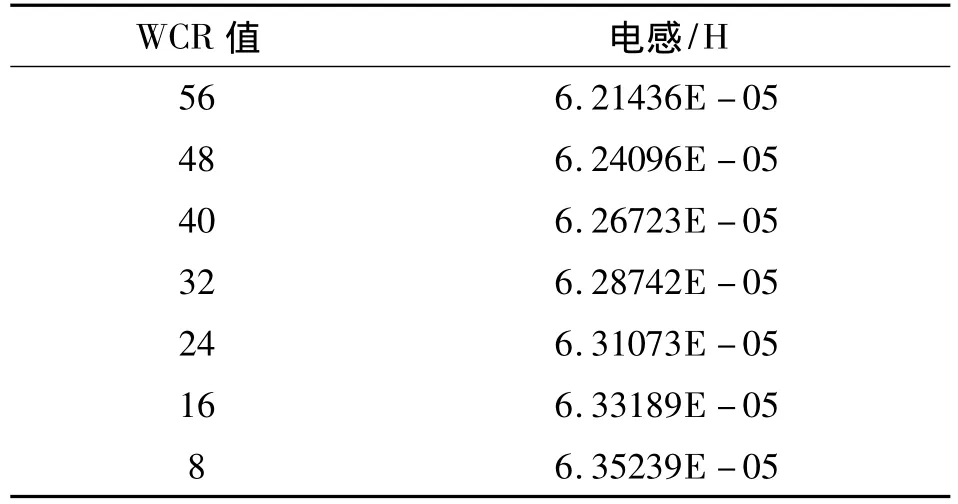
表1 数控可变电感调节实验结果

通过对WCR的阶梯性调节改变电感值，记录结果如图7所示。从结果中可以看出其响应较为迅速，不存在显著的过渡过程，可以适应连续调节。

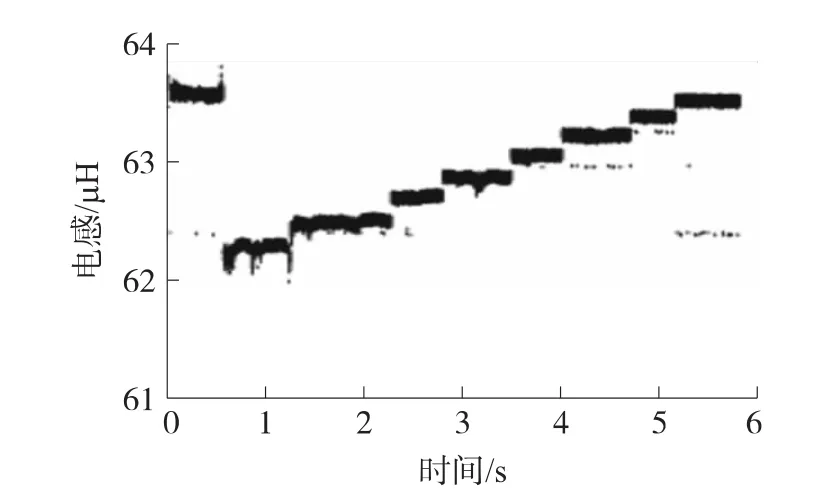
图7 数控可变电感连续调节实验

实验结果表明，所设计的数控可变电感完全可以实现电感的数字可控。但是，由于互感值比较小，因此在k2=10的情况下，调节范围比较小，想获得大的调节范围可以增大k2，或者将比例运算电路改为反相比例放大器。另外，由于控制量k位于式(7)的分母上，它与等效电感值之间不是线性关系，实际使用中需要注意。

4 总结

所设计的数控可变电感在克服了传统机械式可变电感不能实时在线数字化控制的缺点，而且结构简单，设计灵活，可以针对不同的主电感电流、电压要求进行设计，是一种较为方便的电感数字化调节方案。另外，需要指出的是，本文设计的数控可变电感采用了多个集成运算放大器来实现，其适用电压范围、工作频率范围均受集成运算放大器对应性能的影响。

［1］张立科，付永庆，宋宝森.基于网络可操控的电阻元件实现技术［J］.实验室研究与探索，2007，26(3):54-55，60.

［2］张岭，孙宏志，梅栋良，等.基于PSCAD/EMTDC的数控电容在PWM整流器中的应用仿真研究［J］.电子技术应用，2011，37(9):74-76.

［3］Paul R Gray，Paul J Hurst，Steven Lewis.Analysis and Design o Analog Integrated Circuits［M］.John Wiley ＆ Sons Inc，2009.

［4］Hirohito Funato，Kenzo Kamiyama，Atsuo Kawamura.A New In stantaneous Power Flow Control Method Using Variable Inductance Realized by Variable Active-Passive Reactance［J］.T.IEE Japan 2000，120(10):1205-1211.

［5］Cho G C，Jung G H，Cho G H.Analysis and Design of Power Efficient Classed Amplifier Output Stages［J］.IEEE Trans.on Circuits and Systems，1996，11:57-65.

［6］Akira Tanabe，Ken’ichiro Hijioka，Hirokazu Nagase.A Novel Vari able Inductor Using a Bridge Circuit and Its Application to a 5-20 GHz Tunable LC-VCO［J］.IEEE Journal of Solid-State Circuits 2011，46(4):883-892.

［7］Hamill D C，Tavakoli Bina M.The Bootstrap Variable Inductance and Its Applications in AC Power Systems［C］//Applied Power Electronics Conf.，1999，2:896-902.

［8］龙云，肖国春，王兆安.电力电子可变电感的原理与实现［J］.电力电子技术，2006，40(5):13-15.

［9］郑莉平，候浩录，王宏江.空心电抗器电感的解析计算［J］.电子器件，2011，34(4):392-394.

［10］苏振中，武占成，罗锦.瞬态冲击电流测量传感系统的研究［J］.传感技术学报，2002，4:307-310.

［11］胡汉才.单片机原理及接口技术［M］.清华大学出版社，2006 114-117.