SST-LL重力测量卫星轨道分析
覃政 张立华 丁延卫
(航天东方红卫星有限公司,北京 100094)
1 引言
低-低卫星跟踪卫星(SST-LL)模式利用两颗低轨卫星相互跟踪测距,从而感知星下重力异常区域,是利用卫星测量地球重力场的主要方法之一,对测绘、地震、海洋、水文、地球物理、资源勘探、军事等均有非常重要的意义。2002年发射的美德联合研制的“重力恢复和气候实验”(GRACE)双星(至今仍延寿运行),取得了极大的成功,获得了大量的地球重力场原始数据,成为SST-LL重力测量卫星的成功典范。
卫星轨道高度、倾角、偏心率、星间距离等轨道参数,不仅直接影响地球重力场的测量精度和时变特性,还对卫星平台和分系统的设计产生重要影响,是SST-LL重力测量卫星极为重要的系统级参数。本文从卫星工程角度出发,进行SST-LL 重力测量卫星轨道参数的分析和仿真,获得了满足科学任务要求的轨道参数及轨道控制策略,可为我国开展SST-LL重力测量卫星项目提供参考。
2 卫星工作原理及轨道需求
2.1 卫星基本工作原理
卫星系统的基本工作原理如图1所示。在图1中,两颗低轨卫星A、B(图中小车)在同一条极地近圆轨道上编队飞行。当卫星编队经过地球重力异常区域(图中深坑)时,星间相对速度和距离L会发生变化(如图中L1、L2、L3),微米级的精密测距设备可以实时测量星间距离变化量,从而反推出地球重力场的情况(深坑的形状)。
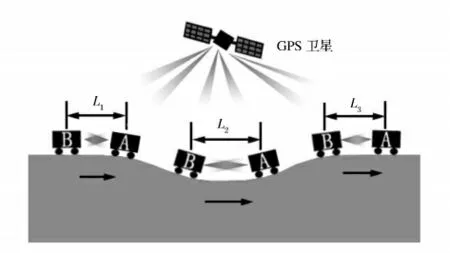
图1 SST-LL模式原理示意图Fig.1 SST-LL gravity satellites system
2.2 轨道需求
目前,SST-LL 重力测量卫星的一般科学目标是:5 000km 重力场波长的大地水准面精度为0.01mm,500~5 000km 波长的大地水准面精度为0.01~0.1mm;以2~4个星期的观测数据测定地球重力场的动态部分。根据上述科学目标,地球物理和地球重力场反演领域的研究人员进行了大量的理论分析,提出了对卫星轨道的一些限制性要求。通过文献调研和分析总结,归纳出了科学目标对卫星轨道参数的具体需求如下。
1)轨道高度
轨道高度与卫星测量的重力场波段相关。轨道越低,重力场中短波信号越强烈,在相同的测量设备精度下,可获得的重力场模型高阶系数精度越高,因此轨道不宜高于500km。此外,由于卫星需要长时间地采集重力场数据来进行时变分析,因此卫星有效工作寿命应不少于5年,在此期间内卫星的轨道高度衰减量应不超过50km[1-2]。
2)地面覆盖性能
卫星的地面覆盖性能主要受轨道倾角的影响。重力场动态测量任务要求卫星在2~4个星期内对全球进行均匀的覆盖,且4个星期内覆盖间隙小于120阶重力场所对应的166km 空间分辨率[1]。为了保证卫星对极地地区的覆盖能力,卫星应采用近极地轨道;为保证极区重力反演精度,星下点轨迹南北极区的覆盖空白直径应小于双星编队距离。
3)轨道偏心率
为保证测量数据的时间均匀性,必须控制卫星在单圈运动过程中的高度波动不超过50km[1],这对轨道偏心率提出了要求。
4)星间距离
两颗卫星距离越远,重力场测量精度越高,但为了控制测量噪声,星间距离不能过大。SST-LL 重力测量卫星的星间距离标称值为220km,且不能超出170~270km 的范围[2-3]。
3 轨道参数分析
在轨道参数分析中,将科学目标对轨道参数的具体需求作为输入条件,采用卫星轨道设计的相关方法对合理的轨道参数取值进行分析,主要从以下几方面展开。
3.1 轨道高度衰减分析
轨道高度自然衰减主要由大气阻力引起。大气阻力与大气密度有关,而大气密度主要受太阳活动率的影响。太阳活动以11年为一个周期,本文采用2000-2011年这11年的太阳活动数据[4],在此基础上采用国际空间研究委员会下属国际基准大气委员会(CIRA)大气模型进行数值仿真[5]。
以500km和450km初始轨道高度的质量500kg、迎风面积1m2的卫星为例,进行仿真分析,其余轨道参数设定为:轨道偏心率e为0.002 0,轨道倾角i为90°。仿真得到的太阳峰年和太阳谷年发射卫星的轨道高度h随时间t的衰减曲线,如图2所示。
由图2可知,500km 初始轨道经过5年将衰减至475km,满足衰减高度不超过50km 的要求;450km初始轨道经过5 年将衰减至380km,衰减高度超过50km。因此,应尽量选用500km初始高度的轨道。
卫星发射时的太阳活动情况影响了轨道高度衰减的历程。由图2(a)可知,太阳峰年发射曲线在中段较为平缓,适于开展长期科学观测;图2(b)显示,太阳峰年发射卫星可获得更长的轨道寿命。综上,卫星太阳峰年发射更有利于测量任务实施。
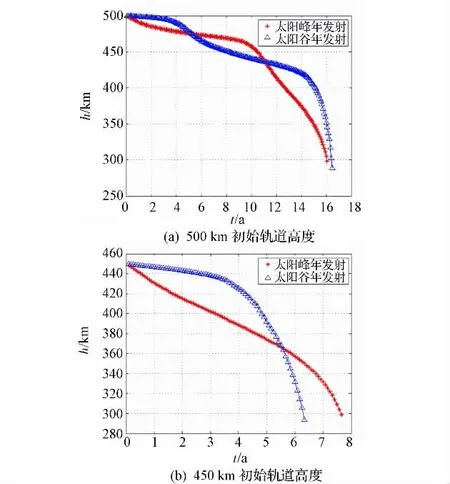
图2 轨道高度衰减仿真结果Fig.2 Simulation results of aerodynamic loss of altitude
3.2 轨道倾角取值影响因素分析
3.2.1 全球覆盖对轨道倾角的要求
为了保证卫星能采集到全球的重力场数据,要求卫星轨道倾角尽量接近90°。
卫星星下点轨迹在极区的空白直径dP为

式中:RP为地球极半径,取值为6 356.755km。
若要求轨道在极区的dP小于星间标称距离220km,则89°<i<91°。
3.2.2 运载能力对轨道倾角的要求
由于倾角为90°的极轨卫星发射时无法借助地球自转速度,若能采用小于90°的顺行轨道,则能节省部分运载能力,提高有效载荷质量。根据调研,SST-LL重力测量卫星单星质量在500kg左右,双星采用支架连接固定在整流罩内,总质量mPL=1.5t。假定采用我国长征-2D运载火箭发射,其主要参数如下:第一级总质量m1为192.3t,燃料质量mP,1为183.0t,比冲Ⅰsp,1为2 550N·s/kg;第二级总质量m2为40.6t,燃料质量mP,2为29.0t,比冲Ⅰsp,2为2 822N·s/kg。二级火箭关机速度vbo可表示为

式中:n1、n2是第一、二级火箭的质量比。
选取3.2.1节结论的下限,即采用89°倾角,最大限度借助地球自转速度,假设火箭关机高度不变,则卫星入轨对火箭关机速度的要求降低了1.1‰,可增加有效载荷质量为Δm,则有
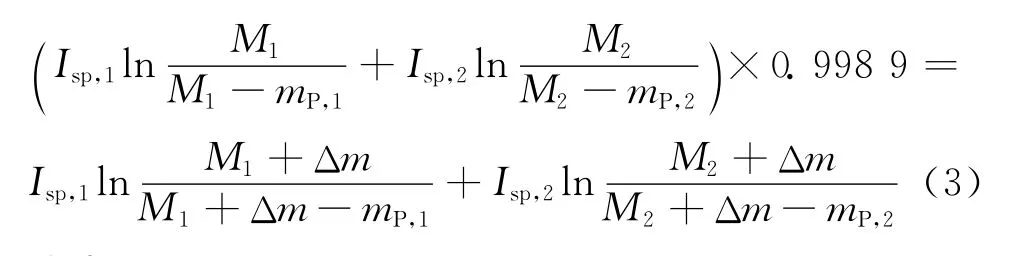
式中:M1=m1+m2+mPL;M2=m2+mPL。
将火箭参数带入式(3)得,Δm=43.2kg。由此可知,若将倾角放宽到89°,单颗卫星至少可增加20kg质量,运载能力增加约3%。
3.2.3 地面覆盖特性分析
下面分析倾角为89°轨道的地面覆盖特性是否满足要求。
近地轨道覆盖特性主要受轨道高度和倾角的影响。为了分析卫星星下点的回归周期,考虑升交点经度λ的变化。在卫星运行一个周期内,λ的变化主要由两部分组成,即地球旋转导致的(Δλ)′2π和地球扁率摄动导致的(Δλ)″2π。两种因素耦合作用,得到λ单圈总变化量(Δλ)2π[5]为

式中:ωE为地球旋转角速度;a为轨道半长轴;μ为地球引力常数;J2为地球扁率摄动常数;RE为长轴半径(即赤道半径),取值为6 378.140km。
若存在正整数X和Y,使得

则在卫星运行Y圈后,星下点轨迹以X天的周期重复,这样的轨道称为回归轨道。将式(4)带入式(5),可得
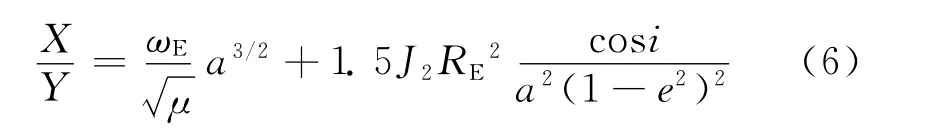
根据反演120阶重力场对4个星期内地面覆盖间隙小于166km 的要求,可知重访圈数Y>240,由式(6)得X>15,结合2~4个星期内进行全球覆盖的要求,卫星的回归周期应尽量在15~30d范围内。3.2.4 考虑轨道高度衰减历程的回归周期分析
随着轨道高度的变化,轨道的回归周期呈现不规则变化,倾角89°轨道的共振回归点分布如图3所示。图3中显示了共振轨道重访天数X与卫星轨道高度h的关系。图中附加了太阳峰年发射的卫星高度自然衰减曲线(图中红色曲线,初始轨道高度为500km),阴影部分为卫星平稳工作时间段。可以看出,当倾角为89°时,卫星平稳工作时间段不包含3d(Ⅰ族)和4d(Ⅱ族)倍数序列,避开了多个重访天数小于15d的共振点,具有良好的地面覆盖特性。

图3 倾角89°轨道随高度衰减所经历的回归周期Fig.3 Repeatable orbit of 89°inclination in life time
3.3 轨道偏心率对单圈高度波动影响的分析
3.3.1 轨道偏心率与地球形状共同影响轨道高度
卫星轨道高度主要受两种因素的影响:一是地球形状,地球的形状为椭球体,赤道半径和极半径的差值ΔhE约为21.4km。二是轨道偏心率e,e的理想值为0.0000,若为0.002 0时,近地点与远地点地心距差值ΔhO约为27.5km。随着近地点的进动,ΔhO与ΔhE相耦合,共同决定了卫星单圈轨道高度变化历程。
3.3.2 轨道偏心率的摄动分析
轨道偏心率矢量的方向由近地点幅角ω来决定。ω的变化主要由地球扁率摄动引起[5],单天ω变化值(Δω)day为
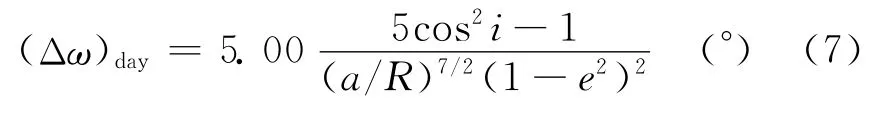
式中:R为地球平均半径,取值为6 371.004km。
经计算,(Δω)day=-3.833°,ω进动360°需94d,远小于卫星寿命。
轨道偏心率的大小受大气阻力影响,有逐渐变小的趋势(圆化效应),因此,只需分析卫星入轨时的初始偏心率,即可保证卫星寿命内偏心率均满足要求。
3.3.3 轨道高度单圈波动分析
设定卫星初始轨道高度为500km,入轨初始偏心率为0.002 0,倾角为90°,近地点幅角在0°~360°变化时,轨道高度h的单圈变化曲线集如图4所示,图中θ为卫星绕地运动真近点角。入轨初始偏心率为0.002 0,可使轨道高度波动范围不超过480~530km,满足SST-LL重力测量卫星轨道高度波动幅度不超过50km 的要求。
3.4 星间距离变化分析
3.4.1 星间距离变化趋势
根据SST-LL重力测量卫星的要求,双星的理想距离为220km。实际上,随着卫星绕地飞行,星间距离L会随时间t发生变化,这种变化表现为短周期波动和长周期变化,如图5所示。
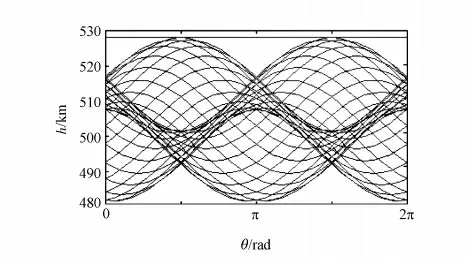
图4 单圈轨道高度变化曲线集Fig.4 Curves of altitude in one circle
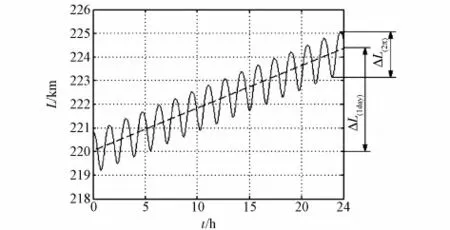
图5 星间距离在1d内的变化Fig.5 Satellite-to-satellite distance change in one day
3.4.2 典型轨道参数对星间距离变化的影响分析
下面分析各轨道参数绝对值及相对差值对ΔL(2π)和ΔL(1day)的影响,结果如表1、2所示。

表1 轨道参数对星间距离的影响Table 1 Effects on satellite-to-satellite distance by orbit parameters

表2 轨道参数差值(前星A-后星B)对星间距离的影响Table 2 Effects on satellite-to-satellite distance by relative differences(A-B)of orbit parameters
由表1可得,SST-LL 重力测量卫星的典型轨道参数对星间距离影响,主要表现在短周期项ΔL(2π),长周期项ΔL(1day)可忽略。由表2可以看出,星间距离L变化主要由di、de和da引起。其中:di、de主要影响ΔL(2π);da主要影响ΔL(1day)。
3.4.3 星间距离变化的控制途径
由3.4.2节分析可知,控制di、de可对ΔL(2π)进行控制,控制da可对ΔL(1day)进行控制。
di、de主要由入轨误差带来,在后期受其他摄动力影响极小,因此只需要在卫星入轨后对di、de进行一次性控制。da主要由轨道半长轴a的变化引起,由前文分析可知,a的变化主要受大气阻力摄动影响。由于双星姿态偏置角及迎风面不同,前后星大气阻力存在差异,因此,双星da会持续变化。国外GRACE卫星采取了一系列构型和气动力学措施,使后星受到的大气阻力比前星大2%[6-7]。
为保证星间距离在170~270km 范围内,需对星间距离长期漂移进行控制,最有效的办法就是定期对大气阻力较大的卫星进行轨道高度抬升。具体方案如图6所示,其中VA和VB分别表示A 星和B星的速度。

图6 星间距离控制模式图Fig.6 Satellite-to-satellite distance control mode
图6中描述了通过轨道机动对星间距离进行控制的模式。B星为后星,受到大气阻力较大,因此轨道高度衰减较快。B 星的初始轨道高度比A 星高30m,星间距离为下限170km,且VB<VA,星间距离逐渐拉大;当B星高度降至与A 星相同时,星间距离正好为上限270km,且VB=VA,此时星间距离开始减小;当B星轨道高度比A 星低30m 时,星间距离为下限170km,且VB>VA,此时,B星启动发动机抬高轨道60m,完成一个控制周期,时间约为90d。
4 结论
本文对SST-LL重力测量卫星的轨道参数进行了分析,得到的主要结论如下。
(1)卫星初始轨道高度为500km 左右,可保证5年轨道高度自然衰减不超过50km。卫星在太阳峰年发射更有利于测量任务实施。
(2)综合考虑地面覆盖效果及火箭的运载能力,在初始轨道高度为500km时,轨道的最佳倾角为89°。
(3)轨道偏心率小于0.002 0,可保证500km以下轨道单圈高度波动幅度不超过50km。
(4)星间距离变化的短周期项主要由di、de引起,长周期项主要由da引起,由于双星受到的大气阻力存在差值,因此,需要不断地对阻力较大的卫星进行轨道抬升,以将星间距离控制在合理范围内。
(References)
[1]姜卫平,章传银,李建成.重力卫星主要有效载荷指标分析与确定[J].武汉大学学报(信息科学版),2003,28(5):104-109
Jiang Weiping,Zhang Chuanyin,Li Jiancheng.Analysis and determination of the major payload indexes for gravity exploring satellite[J].Geomatics and Information Science of Wuhan University,2003,28(5):104-109(in Chinese)
[2]郑伟,许厚泽,钟敏,等.卫星跟踪卫星模式中轨道参数需求分析[J].天文学报,2010,51(1):65-74
Zheng Wei,Xu Houze,Zhong Min,et al.Requirement analysis of orbital parameters in the satellite-to-satellite tracking model[J].Acta Astronomica Sinica,2010,51(1):65-74(in Chinese)
[3]周旭华,吴斌.模拟研究卫-卫跟踪中星间隔的选择问题[J].天文学报,2005,46(1):62-69
Zhou Xuhua,Wu Bin.Discussion on separation parameter from satellite to satellite tracking numerical simulation[J].Acta Astronomica Sinica,2005,46(1):62-69(in Chinese)
[4]National Oceanic and Atmospheric Administration(NOAA).Solar data of sunspot[EB/OL].[2011-05-04].ftp://ftp.ngdc.noaa.gov/stp/solar_data
[5]肖业伦.航天器飞行动力学原理[M].北京:中国宇航出版社,1995
Xiao Yelun.Spacecraft flying dynamical principle[M].Beijing:China Astronautics Press,1995(in Chinese)
[6]Mazanek D D,Kumar R R,Min Qu,et al.Aerothermal analysis and design of the Gravity Recovery and Climate Experiment (GRACE)spacecraft,NASATM-2000-210095[R].Washington:NASA,2000
[7]University of Texas.GRACE data[EB/OL].[2011-05-04].http://www.csr.utexas.edu/GRACE

