多目标优化方法在机器学习中的应用简述

郑秀莲

(泰州机电高等职业技术学校，江苏泰州 225300)

多目标优化方法在机器学习中的应用简述

郑秀莲

(泰州机电高等职业技术学校，江苏泰州 225300)

文章概述了多目标优化方法解决机器学习问题的现状，重点对基于Pareto的多目标优化方法进行分析，通过有监督学习中的分类问题和无监督学习中的聚类问题，表明使用基于Pareto多目标优化方法解决机器学习问题的优点，得到对所解决问题的更深的认识。

多目标优化;有监督学习;无监督学习

一、引言

机器学习可以大致分为三类，一类是有监督学习，该类问题的模型能近似地实现给定的输入数据和输出数据之间的映射，典型的有回归问题或分类问题;二是无监督学习，数据聚类是一个典型的无监督的机器学习，聚类将给定的数据集中的数据分配到不同的簇中，使属于同一簇的数据具有较高的相似度;第三类是强化学习，其目的是在某一特定的环境下，找到一个模型能最大限度地累积奖励。

在机器学习中按词典排序的多目标优化，标量式的多目标优化以及基于Pareto的多目标优化较常用，下面就多目标优化在有监督学习和无监督学习中用法做出具体阐述。

二、多目标优化的有监督学习

多目标优化的有监督学习的关注点是必须产生具备良好性能的学习模型，该模型既对训练数据集有良好的逼近性能，又对测试数据集有效。

近年来，关于将多目标优化算法应用到分类问题中的研究越来越多，分类算法经常使用总体分类精确度为指导标准来构造一个模型，最主要的目标是最大化模型的分类性能。文献中利用多目标优化算法NSGAⅡ来建立对于某个特定的类的分类模型。算法步骤总结如下：

步1：将分类问题转化为一个二维多目标优化问题，确定多目标优化算法的目标为同时最大化精确度和覆盖率;

步2：利用统一的编码形式来表示解(二进制编码字符串)，并通过初始化程序来初始化解集(种群);

步3：对种群中的每个解进行解码，再评估，评估的过程就实现了规则的选取，主要是对规则的前提中所包含的属性集进行筛选;若达到最大迭代次数，则算法终止，输出当前非支配解集;否则，继续执行步4;

步4：利用多目标进化算法NSGAⅡ来产生新一代的种群，转步3。

将该算法应用到一些典型的分类数据集中，并与一般启发算法(如：遗传算法)的实验结果进行比较，结果表明应用多目标进化算法来解决该分类问题效果更好。这主要体现在三个方面：

第一，启发算法搜索到的解之间存在相互支配关系，也就是说启发算法最终搜索到的最优解集不是实际最优的，不能充分满足分类问题的需求。而多目标进化算法最终搜索到的解就是最后一轮迭代产生的非支配集，这些解都是非支配的，不可能存在某个解在各维目标上都优于另一个解。

第二，这里的启发算法其实是一种标量式的多目标优化算法，将多个目标聚集成一个目标来解决，所以算法的搜索空间很小，实验结果表明对于某些数据集，启发算法无法搜索到全局最优解。而多目标进化算法把每个目标看成独立的函数来解决，搜索空间更大，对于实验中的每个数据集，多目标进化算法都能找出全局最优解。

第三，启发算法搜索到的最优解的分布性很差，容易聚集到同一个区域内;而多目标进化算法中本身就带有分布性控制的部分，因而，得出的解能够均匀分布到最优边界上。

如上所述，对于一个分类问题，若要实现最大化模型的分类性能这一主要目标，应用多目标优化算法效果更好，得出的解集更优，实验表明多目标优化算法在分类问题上有很大的应用前景。

在此基础上，产生了越来越多的关于将多目标优化算法应用到分类问题上的深入研究。最大化模型的分类性能是研究的主要内容，同时模型的系统易理解性也是研究的重要内容。文献中详细讲述了如何利用基于Pareto的多目标优化算法来产生易理解的模糊分类规则系统。算法基本思想概括如下：

步1：对数据集做标准化处理，即基于各维属性值的范围做模糊分割，将属性值划分为特定的几个区域值。

步2：初始规则集的产生，基于短规则的原理，只选取前提条件长度较短的规则来构建分类系统，假定对于一个有维属性值的数据集，各个属性值模糊处理后都为个值，现在要选择长度小于等于的规则，则可以产生的规则数为个，由此产生的规则数量仍然很庞大。

步3：应用数据挖掘知识，产生候选规则集。这里产生候选规则集的方法就是一个单目标算法，基本思想就是根据评估标准(如：置信度，支持度，两者的乘积)对步2产生的初始规则集排序来选择指定数量的候选规则，通过对不同标准进行实验，实验结果表明利用置信度和支持度的乘积作为标准选取的候选规则生成的系统，在测试分类时正确率最高。

步4：在候选规则集的基础上应用多目标优化算法抽取候选规则集的一个子集来构成易理解的分类系统。将候选规则集中的每个规则编号，利用二进制串来表示某一分类系统的构成，即二进制串某一位上为1表示对应编号的规则包含在该分类系统中，否则为0表示不包含。由这样的一些二进制串就构成了多目标优化算法的种群，再根据多目标优化算法的原理，经过迭代最后产生的非支配集就是所求的解。

实验结果表明，对数据集的预处理操作可以提高整个算法的效率，利用多目标进化算法产生的分类模型是有效的，且模型比较简单易于被用户理解，此外，文中还对多目标进化算法进行了扩展，即结合了局部搜索算法和规则权重的概念。

总之，从上面两个例子可以看出多目标进化算法在分类问题上的应用是有效的，也具备良好的发展前景。此外，多目标进化算法在有监督学习的其他一些问题上也有研究，如神经网络，系统控制等。这些研究足以表明将多目标进化算法应用到有监督学习问题的解决中是有效的。

三、多目标优化的无监督学习

聚类问题通常被定义为将一个数据集分成几个自然组合，属于同一个组合的数据之间的相似性较大，而不同组合的数据之间的相似性较小。在实践中，聚类往往很难实现，主要是因为对于有的数据集，即使是人工来分类也很难分清数据该属于什么组合;另一个原因就是聚类算法的发展还不成熟，具体实现的过程中只侧重于优化一个目标函数。后来的研究提出了对多个目标进行优化的要求，研究表明多目标进化算法也可以应用到聚类问题中。如提出基于Pareto的多目标聚类算法，该算法中考虑了四个目标：第一个目标是簇的内聚性，该目标偏爱密集型的类;第二个目标是最大化簇之间的距离;第三个目标是减少簇的个数;第四个目标是减少所选的特征数。

将基于Pareto的多目标进化算法应用到聚类问题中的优势也得以证明。算法主要分为两个步骤，首先利用多目标优化算法PESAⅡ来寻求非支配解，再通过分析Pareto最优边界来自动确定簇的个数。文中多目标优化算法的目标为最小化两个目标，这两个目标分别表示簇的紧凑性(如式6)和数据点的连通性(如式7)。簇的紧凑性是指对于某个分割部分的数据点与簇中心点之间的整体偏离值;连通性用于检查相邻区域内的数据点分到同一个簇的可能性。

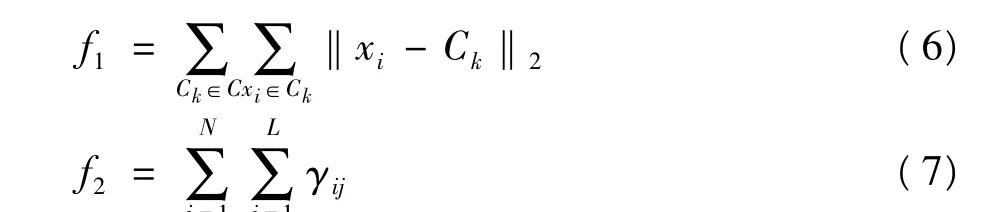
其中C={C1，C2，…，Ck} 是簇的集合，ck是簇Ck的中心，k=1，2，…，K，K是簇的个数，xi是属于簇Ck的一个数据点，L是预先定义的一个领域参数，N是数据集大小，γ定义：若x与NN(x)属于同一个簇，则γ=，否则γ=0。NN(x)是数据点x的第j个邻居点。通过以上的多目标优化算法可以得出一组基于Pareto的非支配解集，这些解都是通过取两个目标函数的折中而得到的，且各个解所包含的簇的数量不同。基于此，算法又设计出一个自动的方法以选择其中某一个解作为最终结果。该自动选择方法根据目标空间的结果图定义了一个关于簇的个数的函数以选择最优解。文中将算法应用到一些数据集的聚类中，并与其他的算法结果进行了比较，实验表明能够找出高质量的解且能够正确的确定簇的个数。

通过实现对多个目标同时进行优化来聚类的，这样的聚类不同于单目标优化算法只局限于优化一个目标而找不到较优的解，通过多目标优化算法找到的解不会只受单一的目标牵制着，能够达到全局优化，因而解的质量更好，效果更佳。以上分析表明，多目标优化算法可以用于解决聚类问题，且在聚类问题的解决中有良好的应用前景。

四、结论

实例表明：源于多目标进化算法本身的特点，使得在解决机器学习问题时，免去了用户对参数设置的责任，也不需要对具有不同意义的目标函数进行整合，多目标进化算法还可以得到一组Pareto最优解集，用户可以从中抽取关于问题的知识，因而在做最后的决策时能做出更好的选择，并得到对问题的更深的认识。

［1］Beatriz de la Iglesia，Mark S.Philpott，Anthony J.Bagnall and Vie J.Rayward－Smith.Data Mining Rules Using Multi－Objective Evolutionary Algorithms.IEEE 2003

［2］Hisao Ishibuchi and Takashi Yamamoto.Fuzzy Rule Selection by Multi－Objective Genetic Local Search Algorithms and Rule Evaluation Measures in Data Mining.Department of Industrial Engineering，Osaka Prefecture University.

［3］H.Abbass，“A memetic Pareto approach to artificial neural networks，”in Proc.14th Aust.Joint Conf.Artif.Intell.，2001，pp.1–12.

［4］S.Park，D.Nam，and C.H.Park，“Design of a neural controller using multi－objective optimization for nonminimum phase systems，”in Proc.IEEE Int.Conf.Fuzzy Sets Syst.，1999，vol.I，pp.533 – 537.

［5］Y.Kim，W.Street，and F.Menczer，“Evolutionary model selection in unsupervised learning，” Intell.Data Anal.，vol.6，pp.531–556，2002.

［6］Julia Handl and Joshua Knowles.Exploiting the Trade－ Off—The Benefits of Multiple Objectives in Data Clustering.Springer－Verlag Berlin Heidelberg 2005.

The Application of Multi－objective Optimization Method in Machine Learning

ZHENG Xiu－lian
(Taizhou Vocational School of Mechanical＆ Electrical Technology，Taizhou Jiangsu 225300)

The article provides an overview of the use of multi－objective optimization methods to solve machine learning problems，focusing on the multi objective optimization method based on Pareto，through the analysis of specific examples，including the classification problem in supervised learning and the clustering problem in unsupervised learning.The author introduces the advantage of the use of multi－objective optimization method based on Pareto to solve machine learning problems，and the users can get to the deeper understanding of problem solving.

multi－objective optimization;supervised learning;unsupervised learning

O153 < class="emphasis_bold">文献标识码：A

A

1671－3974(2012)03－0084－03

2012－05－10

郑秀莲(1985－)，女，大学，泰州机电高等职业技术学校教师，助教，研究方向为计算机软件及网络安全技术。