脉冲时滞Lotka－Volterra食物链系统的正周期解

陈应生，汪东树

（华侨大学 数学科学学院，福建 泉州 362021）

脉冲时滞Lotka－Volterra食物链系统的正周期解

陈应生，汪东树

（华侨大学 数学科学学院，福建 泉州 362021）

利用一些分析技巧和重合度理论，得到一类具有脉冲和时滞Lotka－Volterra食物链系统存在正周期解的新结果.所得的结论表明：脉冲是对该食物链系统正周期解存在性是有影响的 .特别地，在每个种群的内禀增长率（出生率a1和死亡率a2，a3）、种群间相互作用率（捕食率b1，2，b2，3和消化率b2，1，b3，2），以及非线性种内干扰反应系数αi，j都确定的情况下，可以通过适当控制每个种群的（投放率或收回率）hi，k，使每个种群达到平衡（即存在正周期解）.

时滞；脉冲；Lotka－Volterra食物链系统；周期解；重合度理论

对于生物种群系统的持续生存和正周期解的存在性，许多学者已经进行了深入研究，并取得了许多结果［1-5］.文献［1，3］分别研究了具时滞的3种群食物链系统，得到系统存在ω正周期解的一些结果.对于种群生态学而言，脉冲效应是经常存在的，因此研究脉冲种群系统更具有实际意义.本文利用重合度理论，研究脉冲和时滞的非自治周期Lotka－Volterra食物链系统

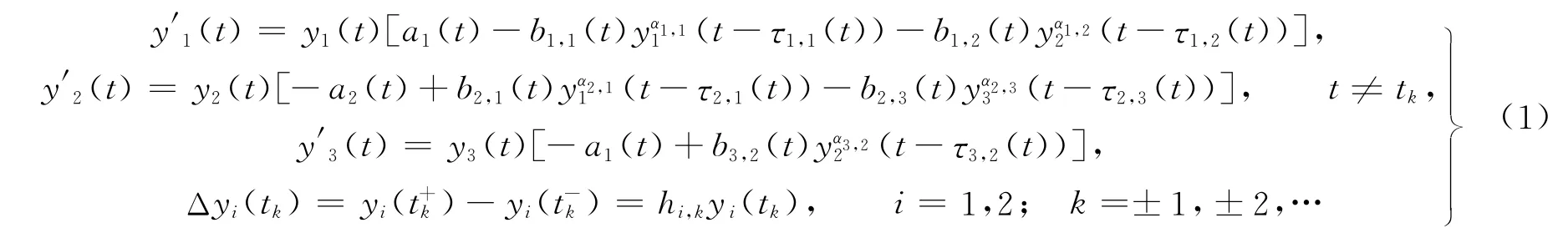
的正周期解的存在性问题.系统（1）满足以下3个假设：1）0＜t1＜t2＜…＜tp＜ω，tk＋p＝tk＋ω且∞，k＝1，2，…；2）｛hi，k｝是一个实序列hi，k，可看成是种群xi在tk时刻的出生率或收获比率，且hi，k＞－1，hi，k＝hi，（k＋p），i＝1，2，3，k＝1，2，…；3）ai（t），bi，j（t），τi，j（t）是非负连续的ω 周期函数，且满足是正常数，i，j＝1，2，3.

1 预备知识

设X，Z是赋范向量空间，L∶DomL⊂X→Z为线性映射，N∶X→Z连续映射.若dim ker L＝co dim ImL＜＋∞，且ImL为Z中闭子集，则称L为指标为零的Fredholm映射.如果L是指标为零的Fredholm映射，且存在连续投影P∶X→X及Q∶Z→Z，使得Im P＝Ker L，ImL＝Ker Q＝Im（IQ），X＝Ker L⊕Ker P和Z＝ImL⊕ImQ，则∶DomL∩Ker P→ImL可逆.

设逆映射为KP，Ω为X中的有界开集，若QN∶¯Ω→Z与KP（I－Q）N∶→X都是紧的，则称N在上是L－紧的.由于ImQ与Ker L同构，因而存在同构映射J∶ImQ→Ker L.

引理1［6］设X，Z，L，N如上定义，而且L是指标为零的Fredholm映射.又设Ω为X 中的有界开集，N在上是L－紧的.假设

2）对任意的x∈∂Ω∩Ker L，QNx≠0；

3）Brouwer度deg｛JQN，Ω∩Ker L，0｝≠0，J，Q如上定义，则方程Lx＝Nx在DomL∩内至少存在一个解.

为运用重合度理论证明主要的结论，需要引入一些函数空间.记

2 正周期解存在性

证明 变换yi（t）＝exp｛xi（t）｝，i＝1，2，3，则系统（1）可化为

记

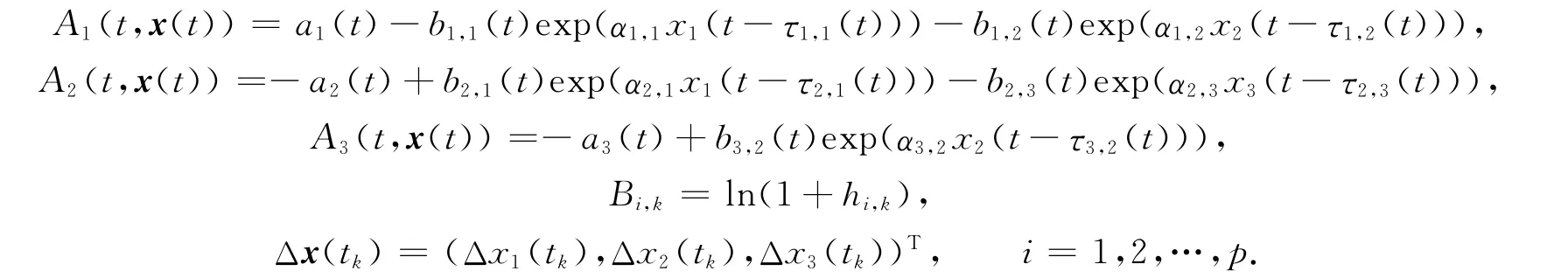
现定义线性算子L∶DomL⊂X→Z为

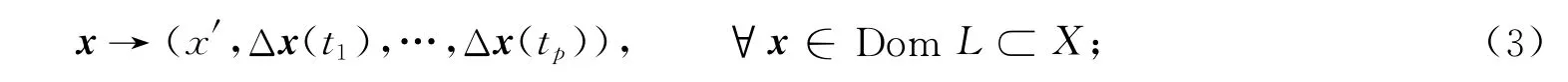
又定义算子N∶X→Z为

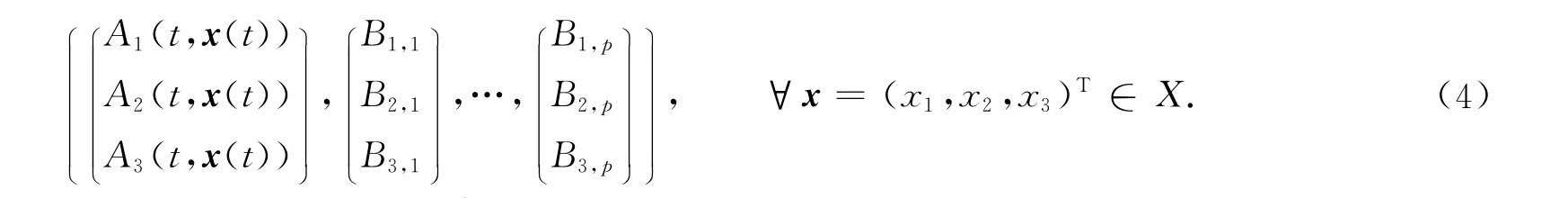
又定义投影算子P∶X→X及Q∶Z→Z为

设x＝（x1（t），x2（t），x3（t））T∈X 是系统（7）对应于某一λ∈（0，1）的解，将式（7）的两端从0到ω进行积分，可得

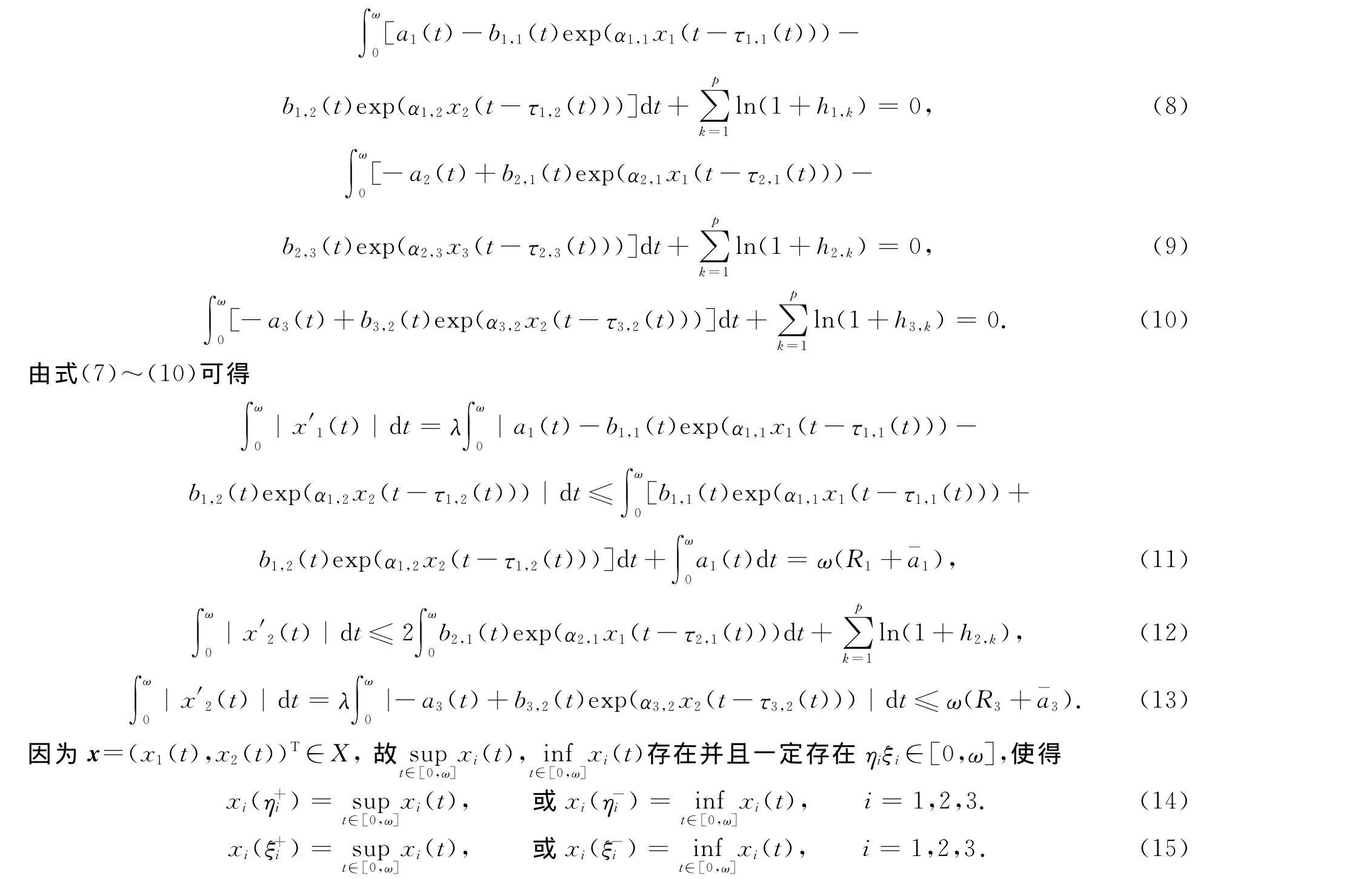
为了方便讨论，不妨设（14），（15）中的第1式成立，至于其他情况，则同理可得以下相同的估计.首先估计xi（t）（i＝1，2，3）的上界.由式（9），（15）可得

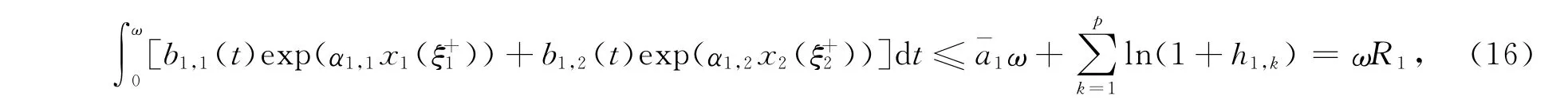
于是有

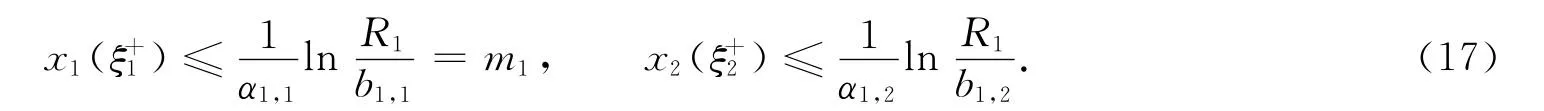
因此，由引理2可知，当t∈［0，ω］时，有

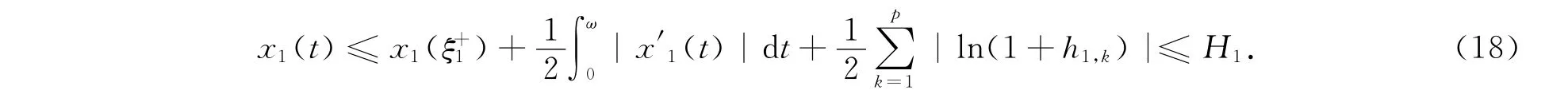
由式（10）和式（15）可得

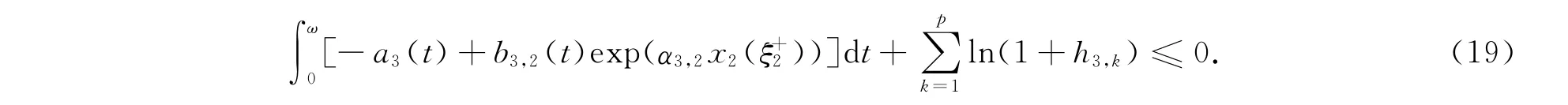
于是有

从而由式（13）与式（20）可知

由式（12），（18），（21）及引理2可知，当t∈［0，ω］时，有

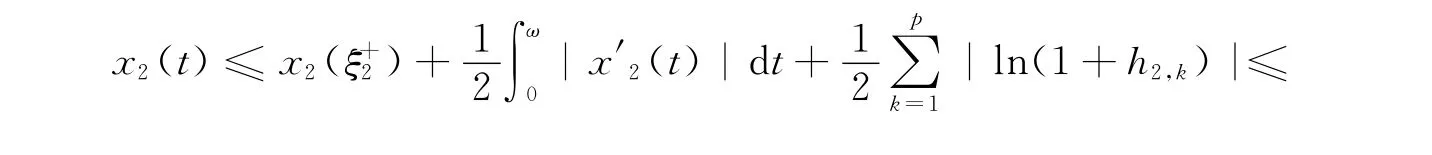
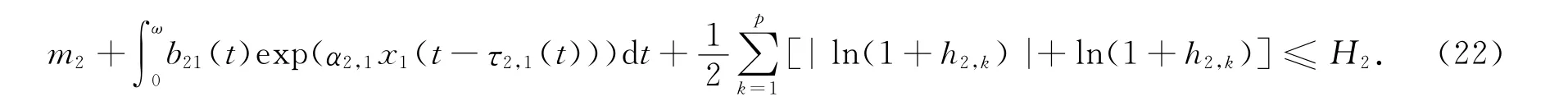
由式（9）和式（15）可得

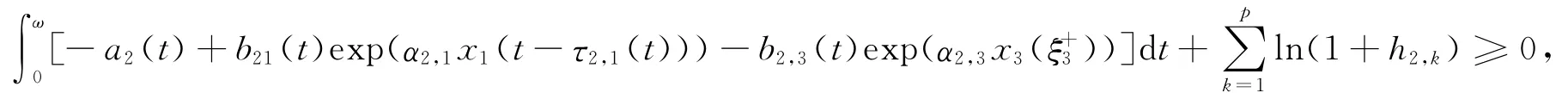
即有

这里ω¯b2，1（exp（α2，1H1）－R2）＞0是由条件保证的，故有

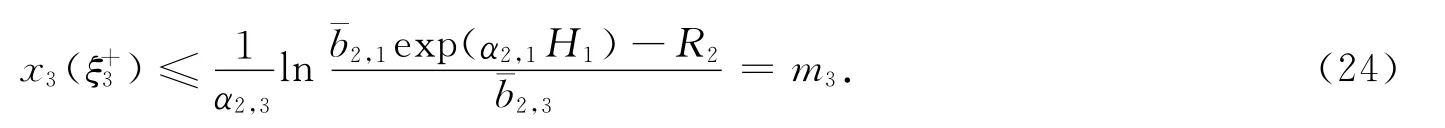
由式（13），（24）及引理2可知，当t∈［0，ω］时，有

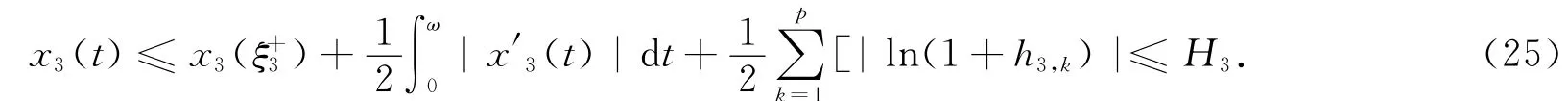
下面估计xi（t）（i＝1，2，3）的下界.由式（9），（14）和（22）可知

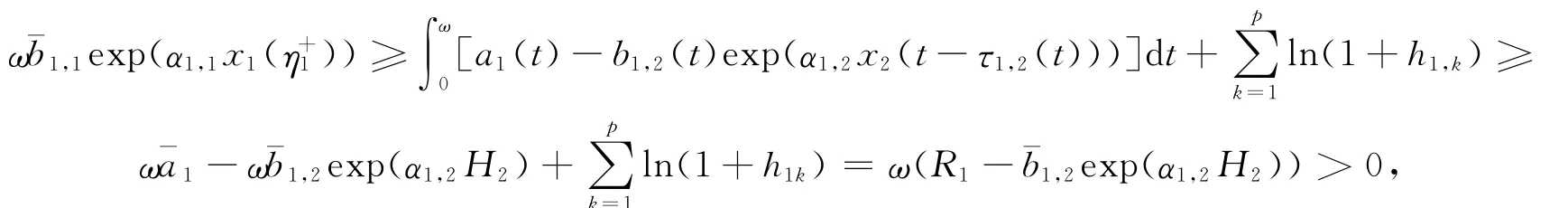
从而有

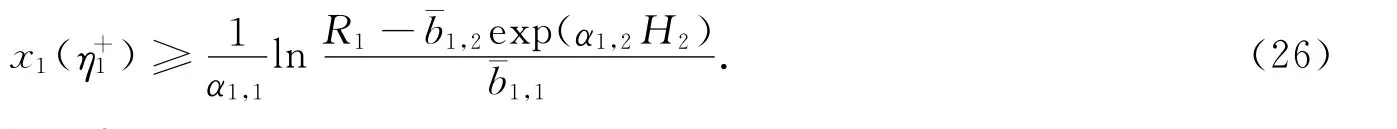
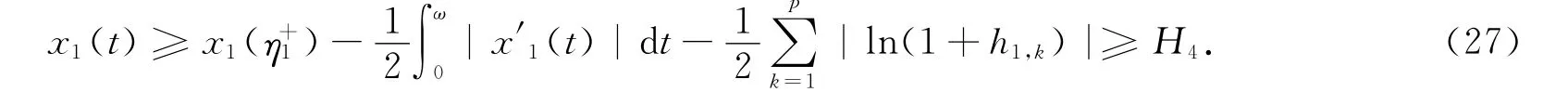
又由式（10）和（14）可知

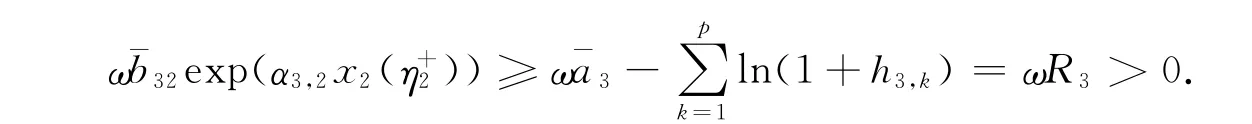
从而有

于是，由式（12），（28）及引理2可知，当t∈［0，ω］时，有

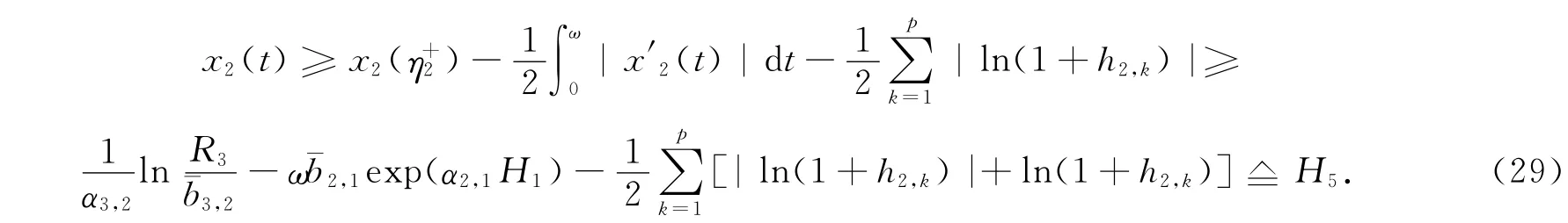
由式（9），（14）和式（28）可知

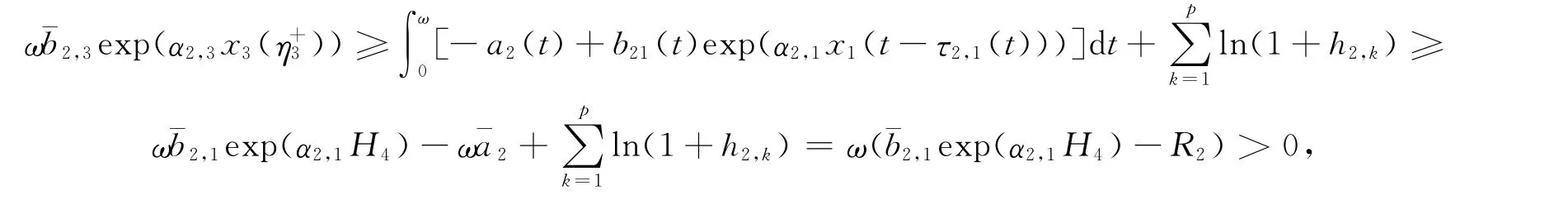
故有

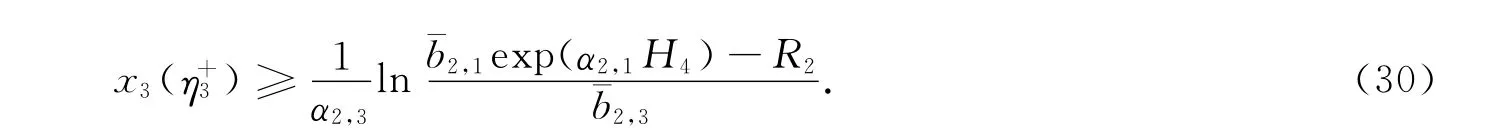
由式（13），（30）及引理2可知，当t∈［0，ω］时，有

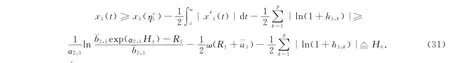
令，由式（18），（22），（25），（27），（29），（31）的讨论可知‖x‖≤H.

显然，正常数H与λ（λ∈（0，1））是无关的.由已知条件易知，代数方程组

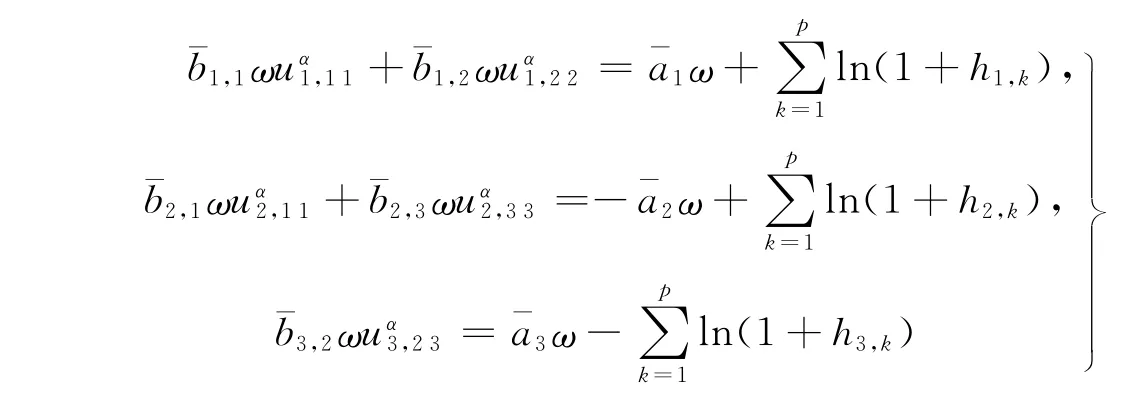
令Ω＝｛x＝（x1，x2，x3）T∈X∶‖x‖＜M｝，则Ω满足引理1中的条件1）.当x∈Ker L∩∂Ω时，x是R3中的常值向量且‖x‖＝M，于是有

即引理1中的条件2）也被满足.下面证明引理1中的条件3）也成立.

从而引理1中的条件3）也满足.因此，系统（1）至少有一个ω－周期解，从而系统（1）至少存在一个正的ω－周期解.

3 应用

下面分别考虑文献［1，3］中研究的具时滞的3种群食物链系统

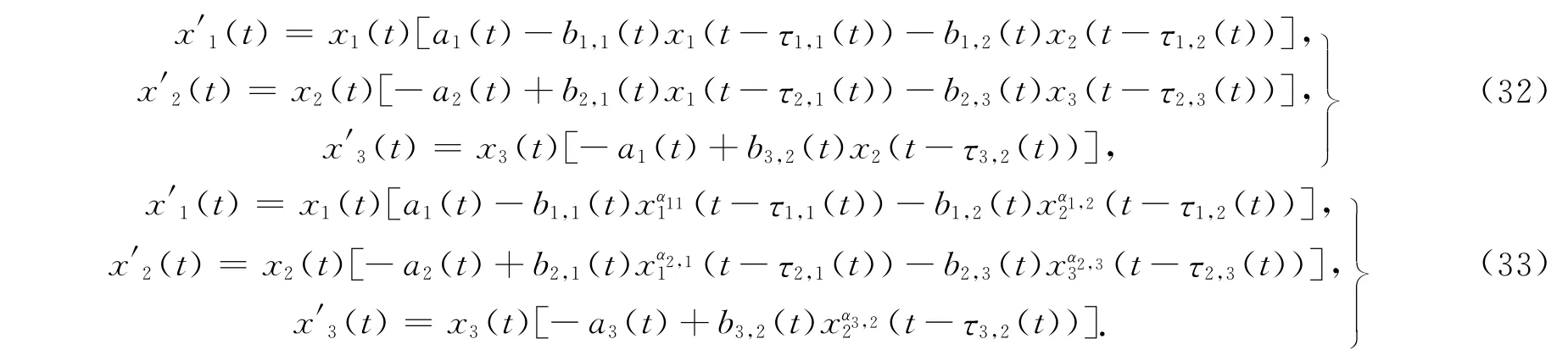
由定理1可得如下定理.

注1 定理2的结果与文献［1］中的主要结果是不相同的，不被文献［1］中的主要结果所包括.

注2 定理3的条件要比文献［3］中的结果成立的条件弱得多，即结论推广并改进了文献［3］中的主要结果.

4 结束语

显然，系统（1）包含了系统（32），（33）.利用重合度理论研究系统（1）的正周期解存在性问题，得出了脉冲对系统（1）的正周期解存在是有影响的新结果.当应用得到的结果研究系统（32），（33）的正周期解存在性问题时，推广并改进了文献［1，3］中的相关结果.这一研究无论是在理论上，还是在物种保护的应用上，都具有广泛的前景和重大意义.

［1］张树文，陈兰荪.具有偏差变元的三种群食物链系统的全局正周期解的存在性［J］.数学杂志，2003，23（1）：125－28.

［2］汪东树，王全义.一类具时滞和比率的扩散系统正周期解［J］.华侨大学学报：自然科学版，2006，27（4）：358－361.

［3］SHEN Chun－xia.Positive periodic solution of a kind of nonlinear food－chain system［J］.Appl Math Comp，2007，194（1）：234－242.

［4］SAITO Y.Permanence and global stability for general Lotka－Volterra predator prey systems with distributed delays［J］.Nonlinear Anal，2001，47（9）：6157－6168.

［5］KORMAN P.Some new results on the periodic competition model［J］.J Math Anal Appl，1992，171（1）：131－138.

［6］GAINES R E，MAWHIN J L.Coincidence degree and nonlinear differential equations［M］.Berlin：Springer－Verlag，1977：40－60.

［7］WANG Qi，DAI Bin－xiang，CHEN Yu－ming.Multiple periodic solutions of an impulsive predator－prey model with Holling－typeⅣfunctional response［J］.Math Comput Modelling，2009，49（9／10）：1829－1836.

Positive Periodic Solutions of a Lotka－Volterra Food－Chain System with Impulses and Delays

CHEN Ying－sheng，WANG Dong－shu
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

By means of coincidence degree theory and some analysis techniques，we obtain a new result on the existence of positive periodic solutions to a Lotka－Volterra food－chain system with impulses and delays.The result showed that impulses have effects on the existence of positive periodic solutions of a Lotka－Volterra food－chain system.Especially，if the growth rate（the birthrate a1and the mortality a2，a2），the population interacting rate（the pery rate b1，2，b2，3and digest rate b2，1，b3，2），and the nonlinear interference reaction coefficient（αi，j）of every one of populations are given，each population may be balanced by controlling the putting rate or recovering rate（hi，k）of every group.

delay；impulse；Lotka－Volterra food－chain system；positive periodic solution；coincidence degree theory

陈志贤 英文审校：张金顺，黄心中）

O 175.6

A

1000－5013（2012）02－0218－07

2011－05－25

陈应生（1976－），男，讲师，主要从事常微分及泛函微分方程的研究.E－mail：cyssheng＠hqu.edu.cn.

国务院侨办科研基金资助项目（09QZR10）；福建省自然科学基金资助项目（Z0511026）