不确定性超混沌系统的自适应鲁棒反同步

李钟慎，傅桂元，杨凯

（华侨大学 机电及自动化学院，福建 厦门 361021）

不确定性超混沌系统的自适应鲁棒反同步

李钟慎，傅桂元，杨凯

（华侨大学 机电及自动化学院，福建 厦门 361021）

针对一类具有外部不确定性的反同步问题，提出一种自适应鲁棒控制方法.基于Lyapunov稳定性理论和自适应控制，设计自适应鲁棒控制器和参数的自适应更新律；通过在输入控制量中引入一补偿项以消除不确定性的影响，实现自适应鲁棒反同步，将系统的反同步误差控制在任意小的范围内.最后，通过数值仿真验证所提出控制方法的有效性.

超混沌系统；反同步；自适应；鲁棒控制；不确定性

同步是指具有相近或相同性质的两个或多个动力系统，通过系统间的相互作用，使得在不同的初始条件下各自演化的动力系统其状态逐步接近，最后达到全同的状态，它是自然界的一种常见的现象［1］.自Pecora和Corroll关于混沌同步的开创性工作［2］以来，混沌同步得到了广泛而深入的研究 .在诸多混沌同步中，反同步也是一个值得关注的现象.所谓反同步就是两个混沌系统的状态变量的绝对值相同但符号相反，即状态变量的和为0的同步现象［3］.超混沌系统一般为具有一个以上正的Lyapunov指数的混沌系统，具有比低维混沌系统更加复杂的动力学特性，使得实现超混沌的控制、同步（反同步）问题成为一项更具有挑战性的研究工作［4］.文献［5］提出了一种基于主动控制和自适应控制相结合的方法，实现对在参数已知和参数未知两种情况下的两超混沌系统的反同步控制.文献［6］基于非线性控制实现两不同结构超混沌系统的反同步.但是，至今含有不确定性的超混沌系统的反同步问题的研究较少，而现实应用中不可避免要受到各种外部不确定性的影响 .因此，研究一类不确定性超混沌系统的反同步问题具有重要的意义.本文设计一种自适应鲁棒反同步控制器，实现一类具有外部扰动不确定性异结构超混沌系统的反同步.

1 问题描述

考虑驱动混沌系统具有的形式为

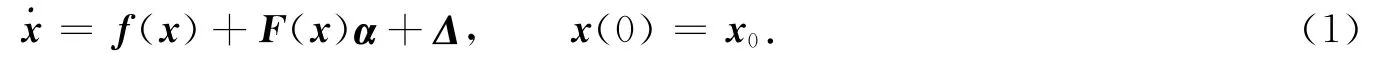
式（1）中：系统状态变量x∈Rn；x0为初始值；未知参数α∈Rm；f（x）为n×1矩阵；F（x）为n×m 矩阵，且Fi，j（x）∈L∞；不确定性项Δ＝［Δ1，Δ2，…，Δn］T为n×1矩阵.假定不确定性项有界，且满足‖Δi‖≤ρi（i＝1，2，…，n ），ρi为已知常数，则记ρ＝［ρ1，ρ2，…，ρn］T.

考虑响应混沌系统的形式为

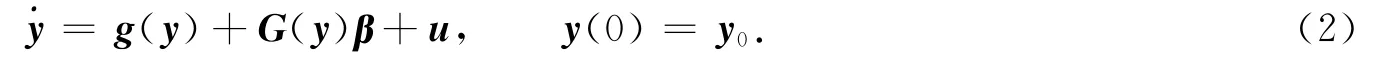
式（2）中：系统状态变量y∈Rn；y0为初始值，且x0≠y0；未知系统参数β∈Rq；g（y）为n×1矩阵；G（y）为n×q矩阵；且Gi，j（y）∈L∞；u∈Rn为系统的控制输入.

定义反同步误差e＝y＋x，设计控制器u的控制目标是使反同步误差e满足

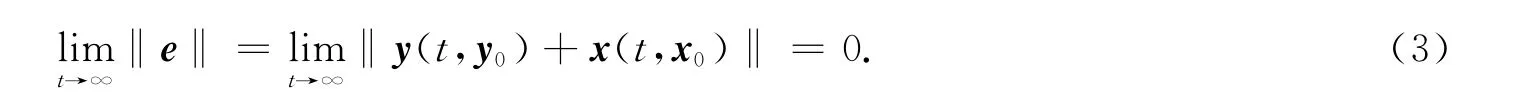
2 反同步控制器设计

将式（1）与式（2）相加，可得系统的反同步动态误差方程为

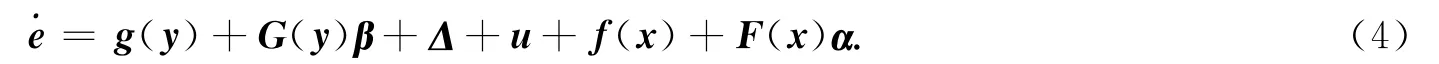
将式（5）沿动态误差系统（4）对时间求导，则可得

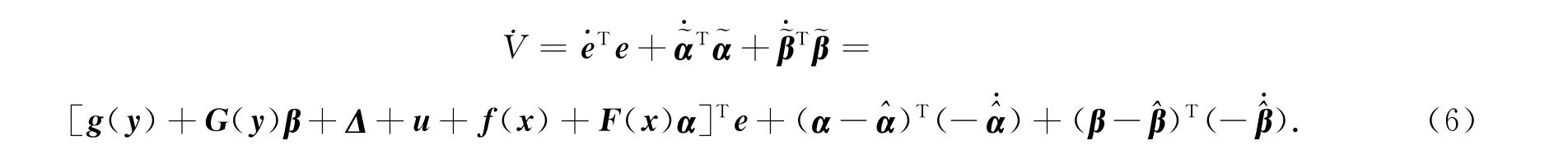
当选取控制器u为

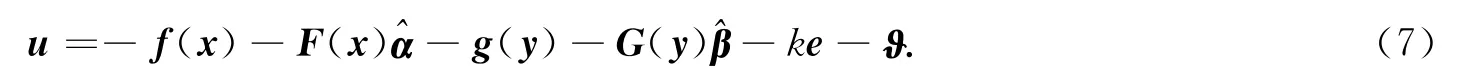
系统参数的自适应律为

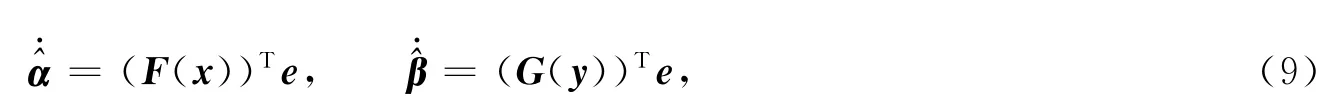
则式（6）可写成如下形式，即

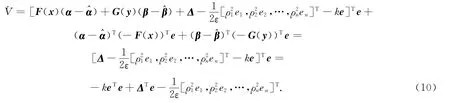
根据Young不等式

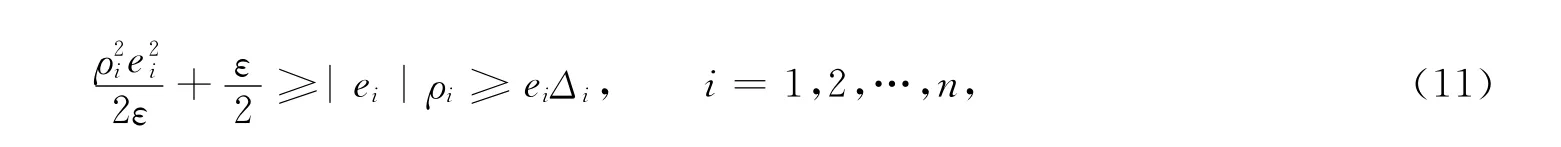
则式（10）可改写为

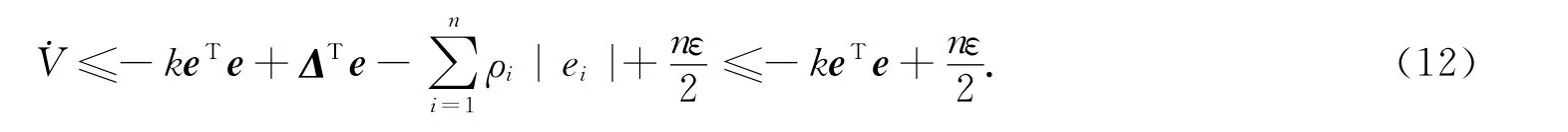
令Γ＝eTe，则Γ≥0.由于ε和k为任意正数，则总是存在ε和k，使得其满足：对∀Γ＞0，有此时˙V＜0.因此，系统（4）将渐近稳定于状态空间原点，系统的误差将处在以为半径的圆内，可以通过选取适当的ε，k值，使误差趋近于无穷小.此时，有

因此，对于被控动态误差系统（4），当采用式（7），（8）所示的控制器及式（9）所示的参数自适应律，则系统将渐近趋于零平衡点，即响应系统（2）将渐近反同步于驱动系统（1）.

3 仿真实例

以超混沌Chen系统［7］和超混沌Lü系统［8］为例，通过数值仿真验证该控制方法的有效性.

3.1 系统描述

假定超混沌Chen系统为驱动系统，写成式（1）的形式，则可描述为

式（13）中：Δ＝［Δ1，Δ2，Δ3，Δ4］T为系统的外部扰动不确定性项，且Δi界限为已知，假定其值为Δ＝［0.25sin（0.25πt），0.8cos（0.5πt），0.9sin（0.6πt），2cos（3πt）］T，则可得其界限ρ＝［0.25，0.8，0.9，2］T.

选取超混沌Lü系统为响应系统，写成式（2）的形式，即

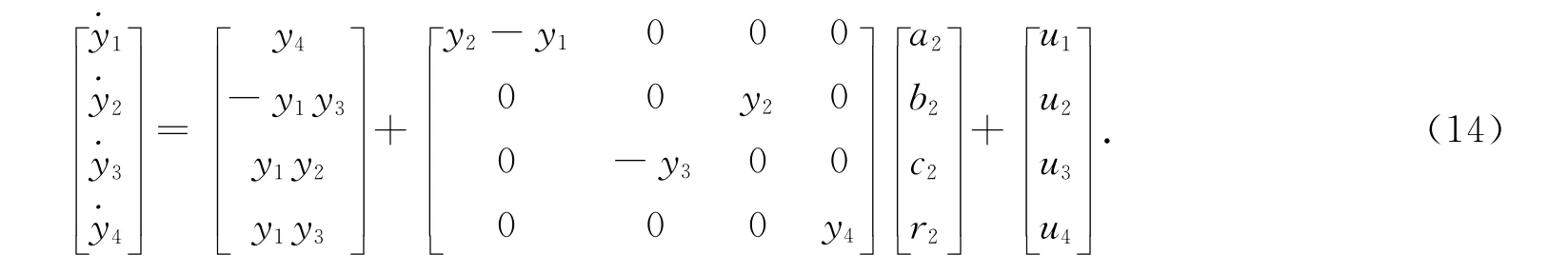
式（14）中：u＝［u1，u2，u3，u4］T为系统的控制输入.当选取系统参数a1＝35，b1＝3，c1＝12，d1＝7，r1＝0.5时，系统（13）表现为超混沌系统特性；而当选取系统参数a2＝36，b2＝3，c2＝20，r2＝1时，系统（14）在未施加控制u 的表现为超混沌系统.系统参数的估计值＾α＝［＾a1，＾b1，＾c1，＾d1，＾r1］T，＾β＝［＾a2，＾b2，＾c2，＾r2］T.

定义系统的反同步误差定义误差为

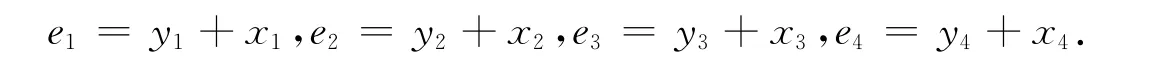
由式（13）和式（14）可得反同步误差动态系统为

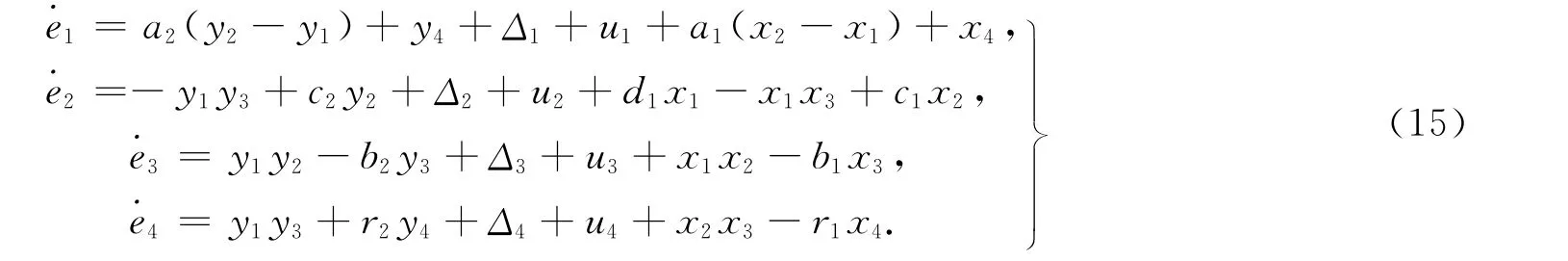
根据式（7），（8），（9）可得自适应鲁棒控制器为

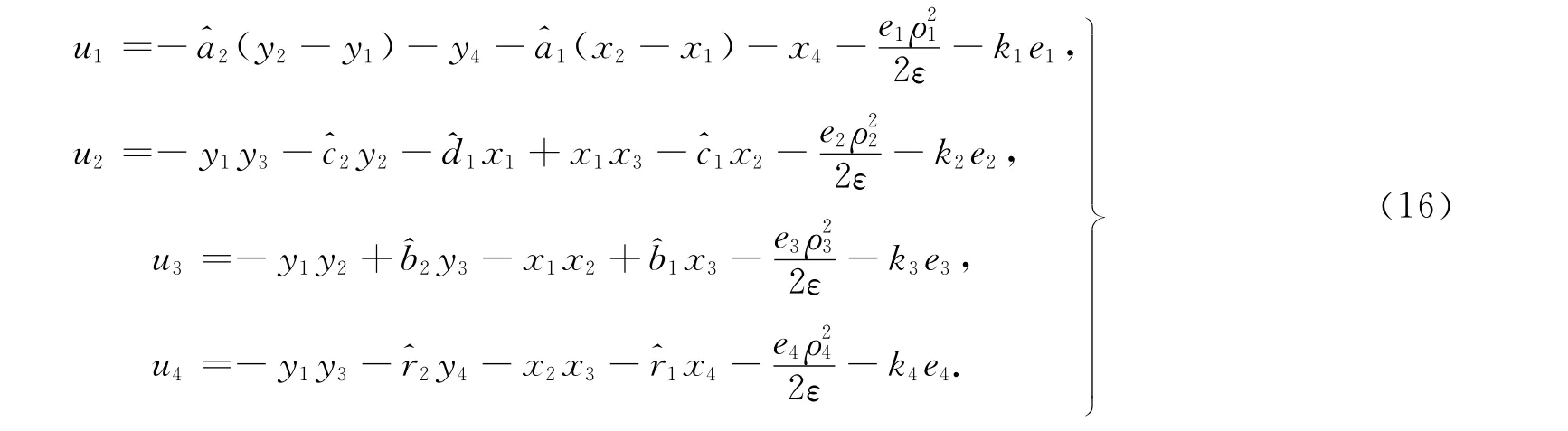
式（16）中：ki＝k（i＝1，2，3，4），ε均为任意大于零的常数.系统参数的自适应律为

3.2 仿真结果

选取超混沌Chen系统各状态变量初值x1（0）＝－2，x2（0）＝－3，x3（0）＝8，x4（0）＝10；超混沌Lü系统各状态变量的初值y1（0）＝5，y2（0）＝8，y3（0）＝－1，y4（0）＝－3，则反同步动态误差变量的初值为e1（0）＝3，e2（0）＝5，e3（0）＝7，e4（0）＝7，参数估计初值＾α（0）＝［4，6，8，10，3］T，＾β（0）＝［5，7，9，11］T；系统的设计参数k＝5，ε＝0.001.

超混沌Chen系统（13）、超混沌Lü系统（14）的反同步各状态变量的时间响应曲线、反同步误差曲线及各参数的估计值，分别如图1，2，3所示 .从图2中可以看出：在控制器（16）的作用下，系统的反同步误差信号快速趋近于零.从图3可知：随着时间t的推移，系统的未知参数也逐渐收敛于稳定值.

图1 超混沌系统各状态变量的时间响应曲线Fig.1 Curve about time response of each state of the hyperchaotic systems

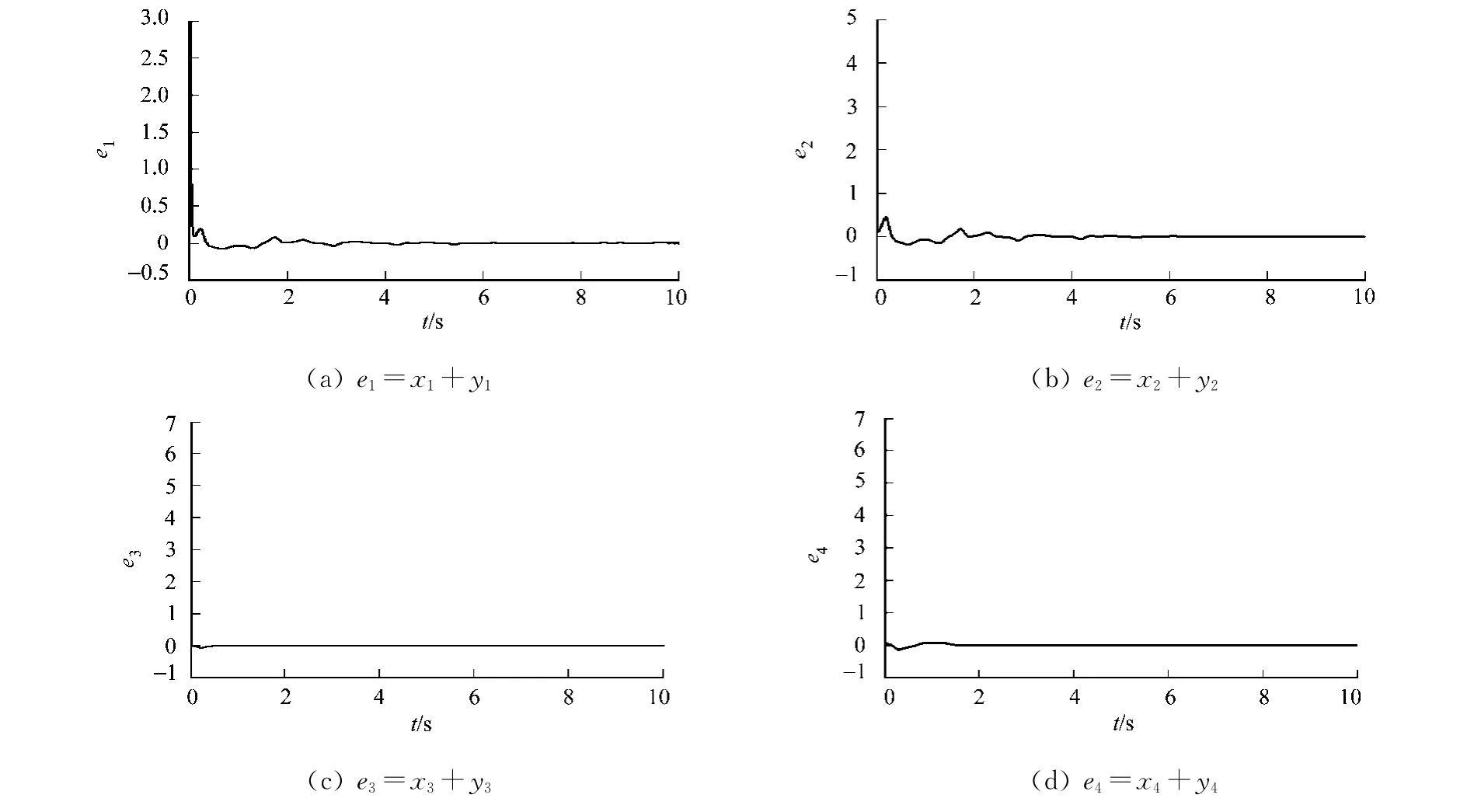
图2 超混沌系统的反同步误差曲线Fig.2 Curve of the anti－synchronization error of the hyperchaotic systems

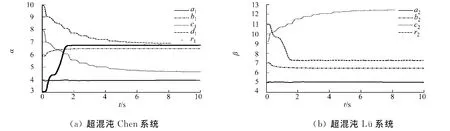
图3 超混沌系统各参数的估计值Fig.3 Estimated value of the parameters of the hyperchaotic systems

4 结束语

研究一类具有外部扰动不确定性的不同结构超混沌系统的鲁棒自适应反同步问题.基于稳定性理论和自适应控制，设计一种改进的鲁棒自适应控制器，通过加入补偿器，消除了不确定性的影响，从而实现系统的反同步及系统未知参数的辨识.通过选择适当的设计参数ε，k，使系统反同步误差趋于无穷小.以超混沌Chen系统和超混沌Lü系统为例，数值仿真结果证明了所提出的控制策略的有效性及具有较强的鲁棒性.该控制方法应用范围广泛，响应速度较快.

［1］傅桂元，李钟慎.无源控制的超混沌Chen系统的自适应同步［J］.华侨大学学报：自然科学版，2010，31（4）：378－382.

［2］PECORA L M CARROLL T L.Synchronization in chaotic systems［J］.Phys Rev Lett，1990，64（8）：821－824.

［3］朱少平.不确定超混沌系统的反同步研究［J］.计算机工程与应用，2011，47（10）：145－145，175.

［4］刘福才，李俊义，臧秀凤.基于自适应主动及滑模控制的分数阶超混沌系统异结构反同步［J］.物理学报，2011，60（3）：030504（1－9）.

［5］WANG Zuo－lei.Anti－synchronization in two non－identical hyperchaotic systems with known or unknown parameters［J］.Commun Nonlinear Sci Numer Simulat，2009，14（5）：2366－2372.

［6］Al－SAWALHA M M，NOORANI M S M.Anti－synchronization of two hyperchaotic systems via nonlinear control［J］.Commun Nonlinear Sci Numer Simulat，2009，14（8）：3402－3411.

［7］LI Yu－xia，TANK W K S，CHEN Guan－rong.Generating hyperchaos via state feedback control［J］.Int J Bifurcat Chaos，2005，15（10）：3367－3375.

［8］CHEN Ai－min，LU Jun－an，LÜJin－hu，et al.Generating hyperchaotic Lüattractor via state feedback control［J］.Physica A，2006，364：103－110.

Self－Adaptive Robust Anti－Synchronization of Hyperchaotic Systems with Unicertainties

LI Zhong－shen，FU Gui－yuan，YANG Kai

（College of Mechanical Engineering and Automation，Huaqiao University，Xiamen 361021，China）

A novel self－adaptive robust control method is proposed to anti－synchronize a kind of hyperchaotic systems with different structures and external uncertainties.Based on Lyapunov stability theory and adaptive control，a self－adaptive robust controller is designed and the updating laws of unknown parameters are given as well.The self－adaptive antisynchronization is achieved by adding a compensator into the input to eliminate the influence of uncertainties，and the anti-synchronization error of a system is bounded within an arbitrarily small value.Numerical simulations are provided to demonstrate the effectiveness of the presented control scheme.

hyperchaotic system；anti－synchronization；self－adaption；robust control；uncertainty

O 19；TP 13

A

1000－5013（2012）02－0129－05

2011－08－11

李钟慎（1971－），男，教授，主要从事先进控制理论与控制工程的研究.E－mail：lzscyw＠hqu.edu.cn.

福建省自然科学基金计划资助项目（2011J01350）；华侨大学基本科研业务费专项基金资助项目（JBZR1107）

（责任编辑：黄晓楠 英文审校：郑亚青）