一类二阶奇异微分方程三点积分边值问题的正解

林秋莲，王全义

（华侨大学 数学科学学院，福建 泉州 362021）

一类二阶奇异微分方程三点积分边值问题的正解

林秋莲，王全义

（华侨大学 数学科学学院，福建 泉州 362021）

研究一类带有积分边值的二阶奇异微分方程正解的存在性问题，应用锥不动点定理及一些分析技巧，得到该边值问题正解存在性的一些新结果.

三点边值问题；二阶奇异微分方程；锥不动点；积分边值；正解

常微分方程的多点边值问题起源于各种不同的应用数学问题，在物理学、化学工程、弹性力学等方面都有着广泛的应用.对于二阶微分方程的三点边值问题，已有许多作者研究并取得一些成果［1-8］.然而，对于二阶微分方程的三点积分边值问题还很少有人研究过.对于二阶奇异微分方程边值问题

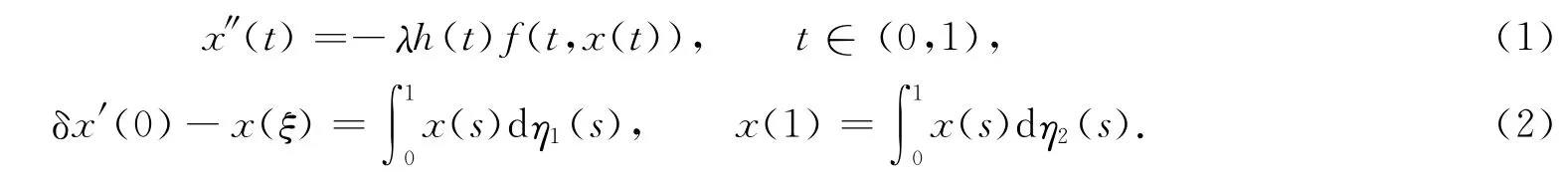
其中：λ＞0，δ≥ξ，ξ∈［0，1］；η1（s），η2（s）在［0，1］上是 Riemann－Stieltjes可积；f∶［0，1］×（0，＋∞）→［0，＋∞）是连续的；h（t）∶（0，1）→［0，＋∞）是连续的，h（t）在t＝0，1和f（t，x）在x＝0处还可能奇异.本文利用锥不动点定理及一些分析技巧，得到了边值问题（1），（2）正解的存在性的一些新结果.

1 预备知识及引理

设X是Banach空间，K⊂X是一个非空子集，且满足1）对任意的u，v∈K和实数α，β≥0，αu＋βv∈K成立；2）若u，－u∈K，则必有u＝0.那么，称K是X 中的一个锥.

引理1［9］设X是Banach空间，K是X中的一个锥.Ω1，Ω2是X中的开集，0∈Ω1，¯Ω1⊂Ω2，T∶K∩（¯Ω2＼Ω1）→K是全连续算子.若满足如下两个条件之一，则算子T在K∩（¯Ω2＼Ω1）中有不动点.

1）若x∈K∩∂Ω1，则；若x∈K∩∂Ω2，则.

2）若x∈K∩∂Ω1，则；若x∈K∩∂Ω2，则.

定义K＝｛x｜x∈X，x（t）≥0，x（t）≥t（1－t），t∈［0，1］｝，易知K 是X 中的一个锥.对任意正常数r，R，R＞r，记

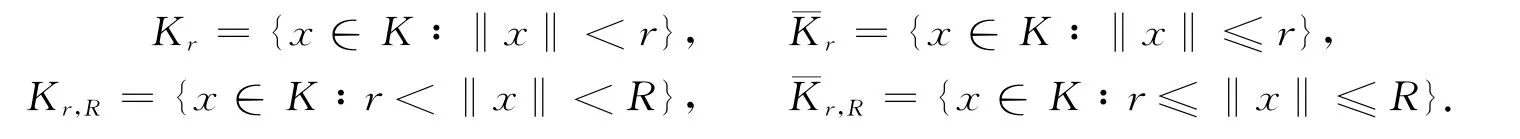
假设下列条件成立，有

H1）η1（t），η2（t），［（δ－ξ）η2（t）－η1（t）］在［0，1］上是非减函数，且

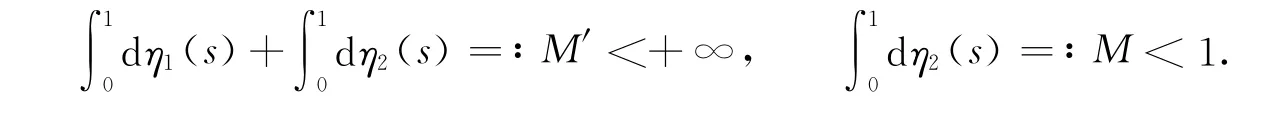
H2）h∈C（（0，1），［0，＋∞）），且在（0，1）的任一子区间上有

式（3）中：ρ＝1＋δ－ξ≥1，有如下几点性质：

A1）当0≤t，s≤1时，G（t，s）≥0，而当0＜t，s＜1时，G（t，s）＞0；

A2）当0≤t，s≤1时，0≤G（t，s）≤G（t，t）≤1－t，G（t，s）≤G（s，s）≤1－s；

A3）当0≤t，s≤1时，G（t，s）≥t（1－t）·G（s，s），G（t，s）≥s（1－s）·G（t，t）；

A4）对任意给定的θ∈（0，1／2），当t∈［θ，1－θ］，s∈［0，1］时，有G（t，s）≥θ（1－θ）·G（s，s）.

引理证略.

现定义线性算子A1∶K→X为

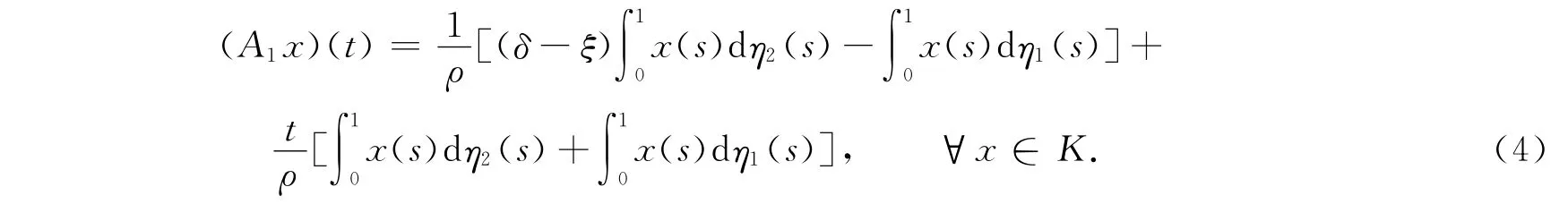
定义算子A2∶K＼｛θ｝→X 为

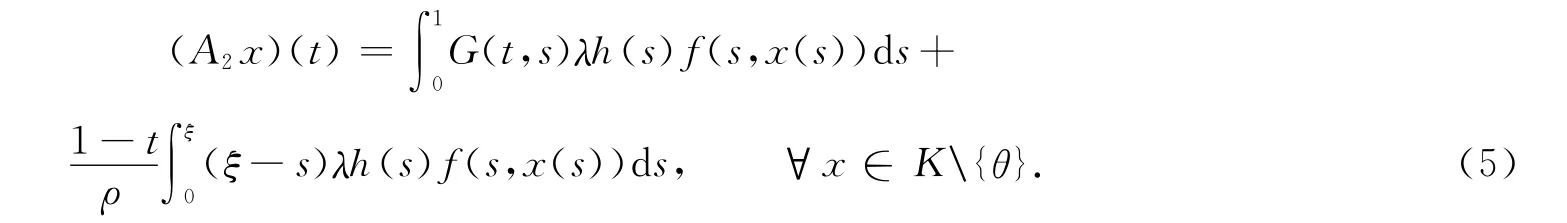
式（5）中：ρ＝1＋δ－ξ，G（t，s）由式（3）给出.易见在条件 H1）～H3）下，上述定义的算子A1x，A2x的右边积分都是存在的.

引理3 在条件H1）下，线性算子A1∶K→K是全连续算子.引理证略.

引理4 在H2），H3）条件下，算子A2∶K＼｛θ｝→K是全连续的.引理证略.

再定义算子T∶K＼｛θ｝→K为

由算子T的定义和上述的引理3，4可知，T∶K＼｛θ｝→K是全连续算子.

引理5 假设条件H1）～H3）成立，如果x＝x（t）是全连续算子T∶K＼｛θ｝→K的一个不动点，则x＝x（t）是积分边值问题 （1），（2）的一个正解.

证明 若x＝x（t）是算子方程Tx＝x的解，则由式（6）可知

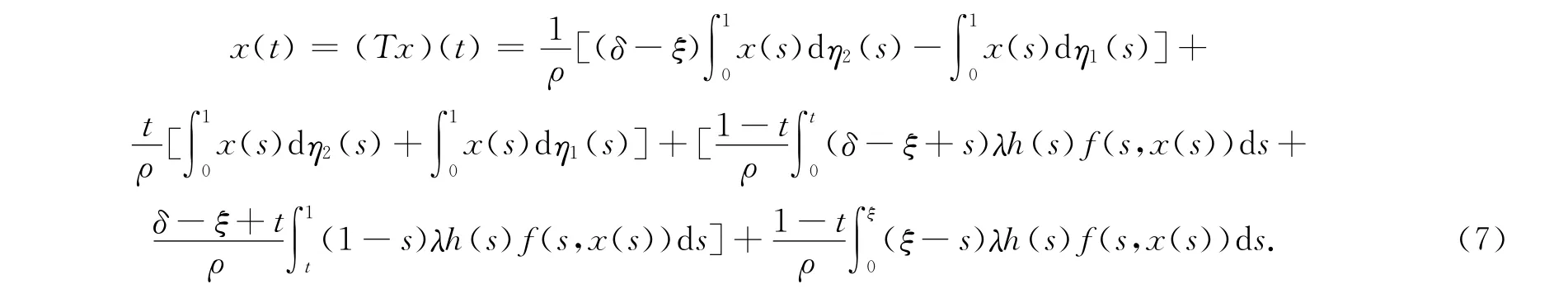
在上式中，分别令t＝ξ，1，则可得

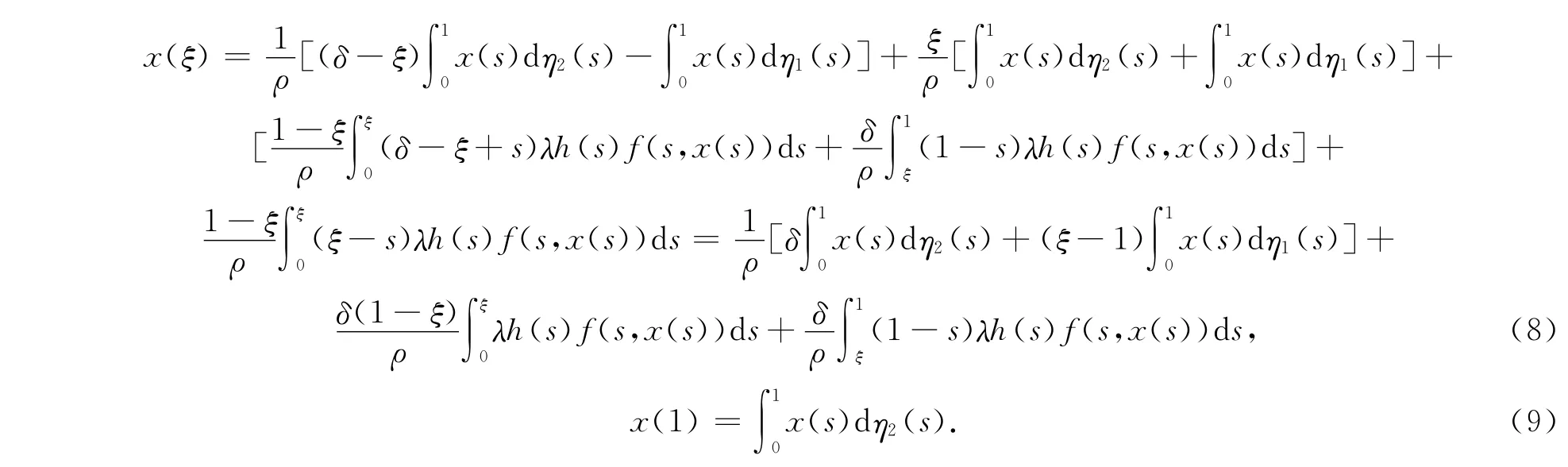
又在式（7）两端对t求导，可得

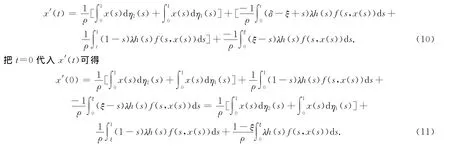
于是，由式（8），（11）可得

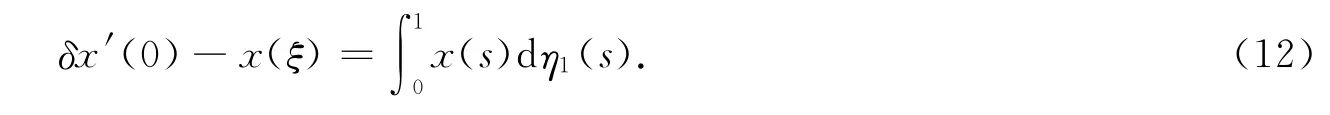
由式（9），（12）即可知式（2）的边值条件也成立.在式（10）两端对t求导，可得

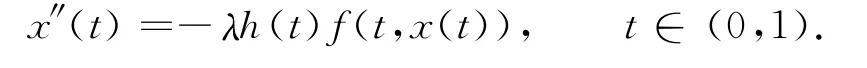
所以，x＝x（t）是积分边值问题 （1），（2）的一个正解.引理5证毕.

2 主要结果及其证明

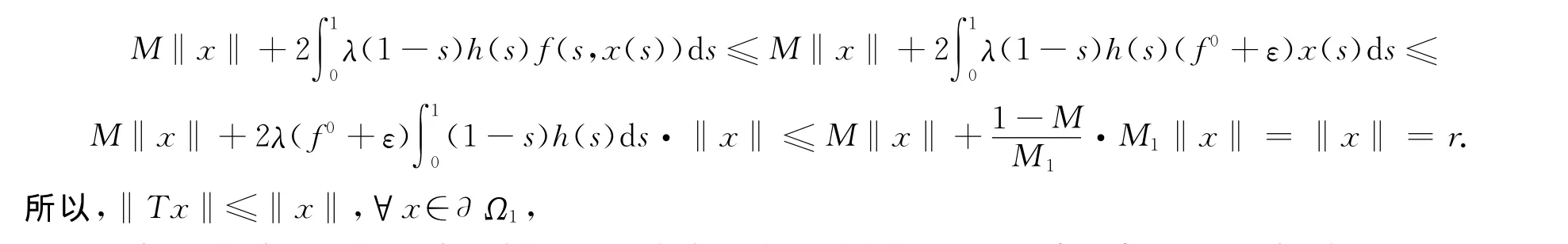
再由f∞的定义可知，对上述的ε＞0，存在一个足够大的R0＞0，使得当x≥R0时，有

取R1＝max｛2r，［θ（1－θ）］－1R0｝.令Ω2＝｛x∈K∶‖x‖≤R1｝，对任意的x∈∂Ω2，‖x‖＝R1.于是，当t∈［θ，1－θ］时，x（t）≥θ·（1－θ）‖x‖＝θ·（1－θ）R1≥R0.因此，由式（6）可得

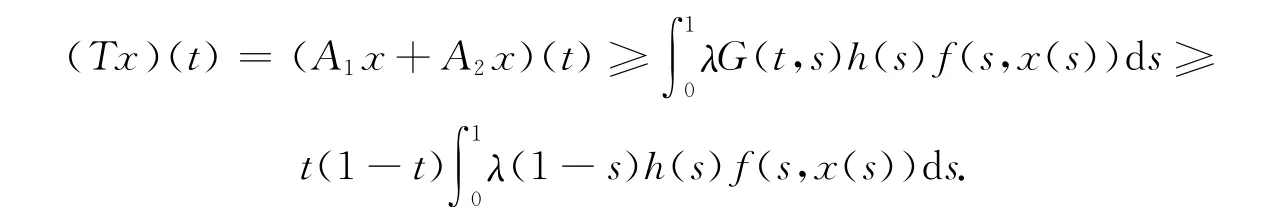
故由式（14）及上式可得

再由引理1可得，算子T在K∩（¯Ω2＼Ω1）中有不动点x＊.又因为x＊（t）≥rt（1－t）＞0，∀t∈（0，1），所以x＊是一个正解.又由引理5可知，边值问题（1），（2）存在一个正解.定理1证毕.

由定理1的证明，易见以下推论1成立.

推论1 假设条件H1）～H3）成立，如果下列条件之一成立：

所以，‖Tx‖≥‖x‖，∀x∈∂Ωr.

又由f∞的定义可得，对上述的ε＞0，存在一个足够大的R0＞0（R0＞2r），使得当x≥R0时，有

同理由定理2的证明，易见以下推论2成立.

推论2 假设条件H1）～H3）成立，如果下列条件之一成立：

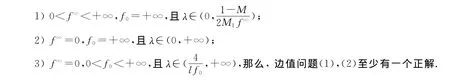
注1 在推论2中，f0＝＋∞可以对应于f（t，x）在x＝0奇异的情形.

3 应用举例

考虑如下的二阶奇异微分方程的积分边值问题

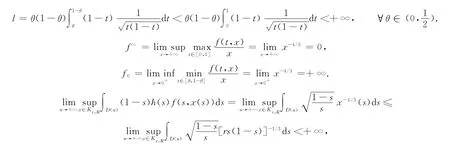
其中：D（n）＝［0，1／n］∪［n－1／n，1］.又λ＝1∈（0，＋∞），故推论2中条件2）的所有条件都被满足，因此边值问题（17）至少有一个正解.

［1］KONG Ling－ju.Second order singular boundary value problems with integral boundary conditions［J］.Nonlinear A－nalysis，2010，72（5）：2628－2638.

［2］JIANG Ji－qiang，LIU Li－shan，WU Yong－hong.Second－order nonlinear singular Sturm－Liouville problems with integral boundary conditions［J］.Applied Mathematics and Computation，2009，215（4）：1573－1582.

［3］SUN Yan，LIU Li－shan，ZHANG Ji－zhou，et al.Positive solutions of singular three－point boundary value problems second－order differential equations［J］.Journal of Computational and Applied Mathematics，2009，230（2）：738－750.

［4］曹君艳，王全义.一类二阶微分方程两点边值问题的正解存在性［J］.华侨大学学报：自然科学版，2010，31（1）：113－117.

［5］ZHANG Xue－mei，FENG Mei－qiang，GE Wei－gao.Multiple positive solutions for a class of m－point boundary value problems［J］.Applied Mathematics Letters，2009，22（1）：12－18.

［6］FAN Hong－xia，MA Ru－yun.Loss of positivity in a nonlinear second order ordinary differential equations［J］.Nonlinear Analysis，2009，71（1／2）：437－444.

［7］LI Gao－shang，LIU Xi－ping，JIA Mei.Positive solutions to a type of nonlinear three－point boundary value problems with sign changing nonlinearities［J］.Computers and Mathematics with Applications，2009，57（3）：348－355.

［8］ZHAO Jun－fang，GE Wei－gao.A necessary and sufficient conditions for the existence of positive solutions to a kind of singular three－point boundary value problem［J］.Nonlinear Analysis，2009，71（9）：3973－3980.

［9］郭大钧.非线性泛函分析［M］.济南：山东科学技术出版社，2001.

Positive Solutions of Three－Point Integral Boundary Value Problems for A Kind of Second－Order Singular Differential Equations

LIN Qiu－lian，WANG Quan－yi
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

In this paper，we study the problems on the existence of positive solutions for a kind of second－order singular differential equations with integral boundary value.By means of the cone fixed point theorem and some analysis skills，we get some new results on the existence of positive solutions for the boundary value problem.

three－point boundary value problem；second－order singular differential equations；cone fixed point；integral boundary value；positive solutions

钱筠 英文审校：张金顺，黄心中）

O 175

A

1000－5013（2012）02－0212－06

2011－05－23

王全义（1955－），男，教授，主要从事常微分方程和泛函微分方程的研究.E－mail：qywang＠hqu.edu.cn.

国务院侨办科研基金资助项目（09QZR10）