The Budget Constrained Multi-product Newsboy Problem with Reactive Production: A Problem from Entrepreneurial Network Construction∗

LI WEN-JINAND PANG YAN-NI

(1.School of Management,Jilin University,Changchun,130025)

(2.School of Mathematics,Jilin University,Changchun,130012)

The Budget Constrained Multi-product Newsboy Problem with Reactive Production: A Problem from Entrepreneurial Network Construction∗

LI WEN-JIN1AND PANG YAN-NI2

(1.School of Management,Jilin University,Changchun,130025)

(2.School of Mathematics,Jilin University,Changchun,130012)

This paper develops an extended newsboy model and presents a formulation for this model.This new model has solved the budget contained multi-product newsboy problem with the reactive production.This model can be used to describe the status of entrepreneurial network construction.We use the Lagrange multiplier procedure to deal with our problem,but it is too complicated to get the exact solution.So we introduce the homotopy method to deal with it.We give the flow chart to describe how to get the solution via the homotopy method.We also illustrate our model in both the classical procedure and the homotopy method.Comparing the two methods,we can see that the homotopy method is more exact and efficient.

newsboy problem,entrepreneurial network,construction,multi-product, budget constrained,reactive production,homotopy method

1 Introduction

The classical newsboy problem is a single period stochastic inventory model.Harris[1]presented a formula for the optimal economic order quantity(EOQ)in simple inventory models. Afterwards,much more attention was paid to the character of the single period product, and this problem was called single-period problem(SPP)or newsboy problem(NP).Hadley and Whitin[2]developed the constrained newsboy problem in 1963.Khouja[3]classi fi ed the extensions into 11 categories in 1999.The newsboy problem with reactive production isnot in the 11 extensions.Chung and Flynn[4]first developed this extension to the newsboy problem in 2001,and they divided the production into two stages,an anticipatory stage and a reactive stage.But there are two aspects of localization in[4],only one product is concerned and there are no budget constraints to the production.Some constrained newsboy problems have been studied(see[4–6]).

In today’s supply chain management,the most frequent instance we have to face is the newsboy problem which contains multiple products and has to constrain the budget.If the products are seasonal products with a long-selling season and a highly volatile stochastic demand,we have to divide the production into two parts,an anticipatory stage and a reactive stage.So we extend the newsboy problem to deal with this situation.In this paper we consider the newsboy model which contains multiple products.The production occurs in two stages,an anticipatory stage and a reactive stage.The budgets in both stages have to be constrained.It can be explained as follows.There are several products that are all the seasonal ones.And each of them has a highly volatile stochastic demand.The demand of each product is very high at the peak period and is negligible at the o ff-peak period.Chung and Flynn[4]said that if this situation was solved by the classical newsboy problem model, it leads to a low service level or a highly volatile demand.Both of the two results are not what we want to see.So Chung and Flynn[4]modi fi ed the classical model,and introduced two production periods,which are the anticipatory stage and the reactive stage.

In the real world,the budgets in both of the two production periods should be constrained.Our main work is to find whether the optimal order quantities for each product in the two stages exist or not.To solve our problem,we can follow the classical procedure which is used to solve the constrained multi-product newsboy problem.However,it is too complex for us to get the exact solution of the model.So we introduce a new method,the homotopy method,to deal with our problem.We illustrate our model in both the classical procedure and the homotopy method.Compared with the two methods,we can find that the homotopy method is more exact and efficient.In entrepreneurial network construction, we face that the energy is constrained.So we must optimize the network,as the budget is constrained in[7].

This paper is organized as follows.In Section 2,we give a brief review of the newsboy Problem.We uniformize the formula into the same parameter,and give the solution procedure.In Section 3,the model formulation of our problem is given.We use the classical procedure and the combined homotopy interior point method to deal with our problem respectively.And then compared with the two procedures,we find the better one.In Section 4,We give a numerical example to illustrate our solution procedure.

2 A Brief Review of the Newsboy Problem

In this section,we review the classical newsboy problem and its two extensions.First,we give some notations and assumptions.

2.1 Notations and Assumptions

Notations:

N the amount of products;

cicost per unit for product i;

rcicost per unit for productiin reactive production;

piselling price per unit for product i;

sisalvage value per unit for product i;

licost of lost sales per unit for product i;

clichance loss value per unit for product i;

Qiorder quantity for product i;

RQiorder quantity in reactive production for product i;

SLiservice level for product i;

Dia random variable of the demand for product i;

fi(·) demand density function for product i;

Fi(·) cumulative demand function for product i;

C the budget constraint of products’cost;

RC the budget constraint of products’cost in reactive production.

Assumptions:

(1) li=(pi−ci)+cli;

(2) 0＜si＜ci＜rci＜pi;

(3) SLi=Fi(Qi);

(4) 2ci＞rci+si;

(5) all the products demands are independent.

These assumptions can be explained as follows:

(1)means that the cost of lost sales consists of two parts,which are the pro fi t in the normal instance and the chance loss value.(2)means that if the order quantity exceeded a real demand,the product would be sold at a salvage price which is much lower than the cost of the product.(3)gives us the formula to count each product’s service level.(4)means that the reactive production may save the cost.

In our problem,there are many products,and their demands are all independent.

2.2 The Classical Model and Its Extensions

One of the classical newsboy formulation is to minimiaze each product-i’s risk-neutral expected cost function as follows:

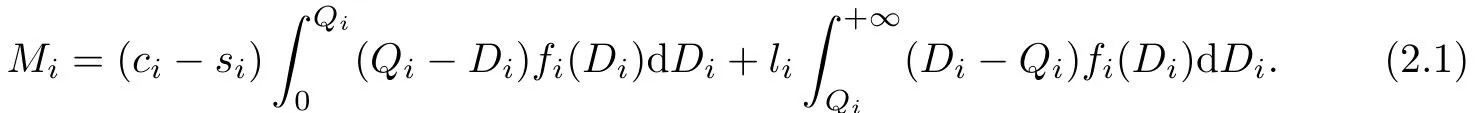
In order to find product-i’s optimal order quantity and optimal service level that minimize Mi,we solve

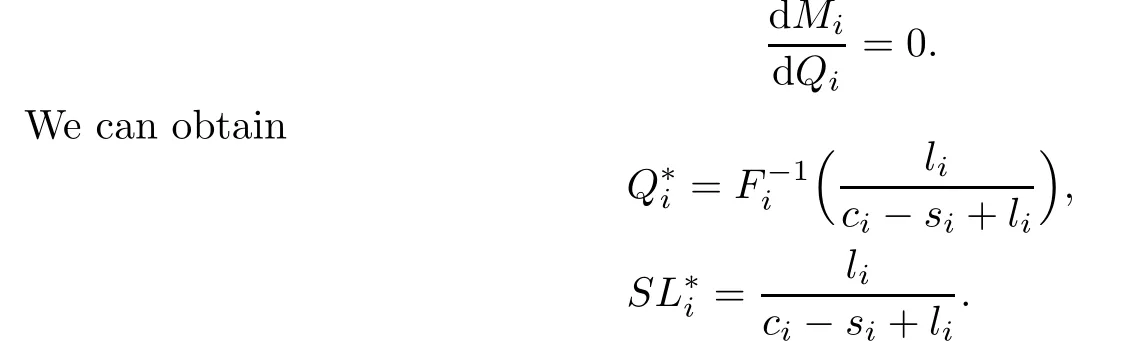
There are many extensions to the classical newsboy problem.Among them the extension to budget constrained multi-product is very important,because we never sell only one product and the budget is always constrained in the real world.

Hadley and Whitin[2]originally introduced the multi-product constrained model as follows:

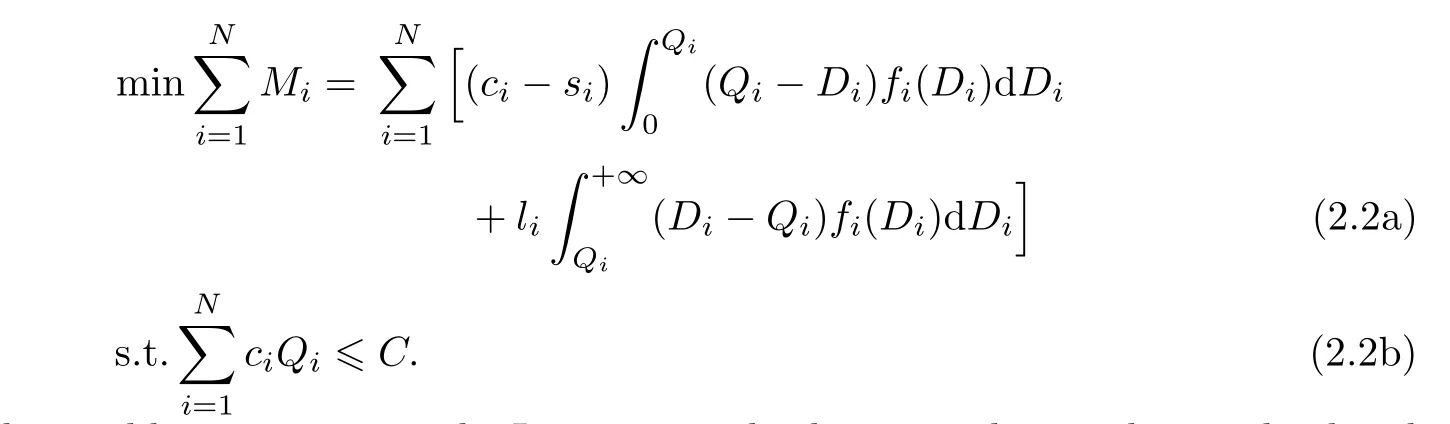
To solve this problem,we can use the Lagrange multiplier procedure and omit the detail of this procedure here.In next section we use it to deal with the new model.

3 Model Formulation

Our main work is to formulate a model to extend the budget constrained multi-product newsboy problem with reactive production.First we represent the formula of the model with a reactive production.different from Chung and Flynn[4],the formula in our paper is presented with the classical frame.We use the same parameters as in Section 2.

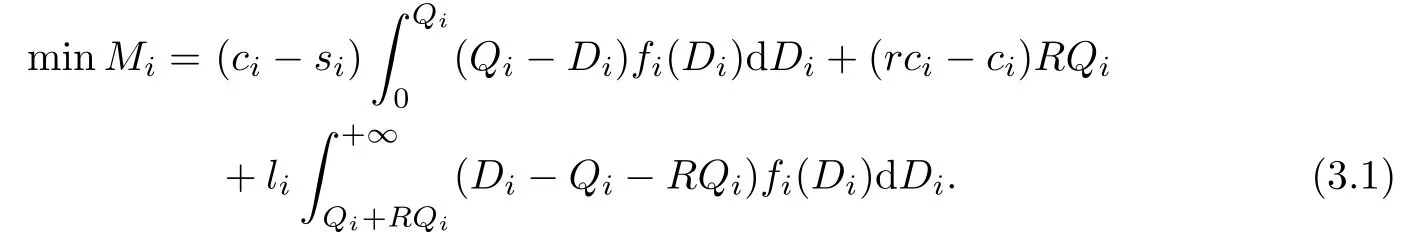
To get the optimal order quantity,we solve

We obtain

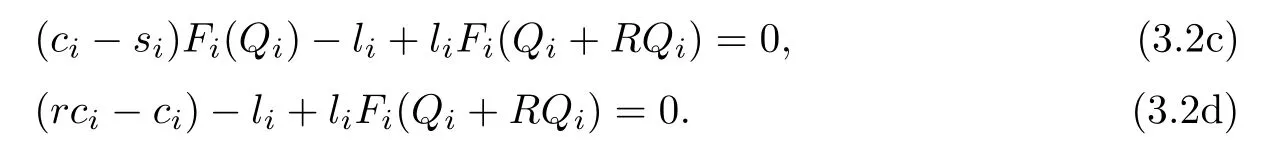
The optimal order quantity can be expressed as follows:

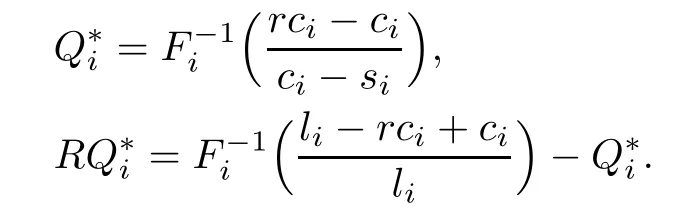
In this model,we also want to get the optimal service level for each product.However it is too complex,because of two stages and that the production occurs between them.So we de fi ne the optimal service level in each stage,and the optimal service level of the whole in the model can be calculated from the two service levels.

The optimal service level in the anticipatory stage is

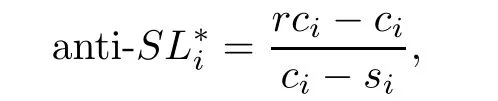
and the optimal service level in the reactive stage is

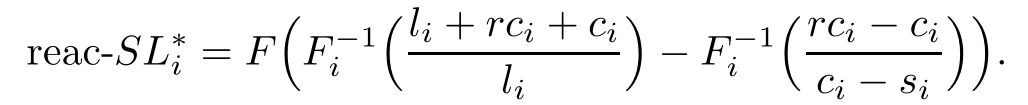
Then the optimal service level of the whole stage can be de fi ned as

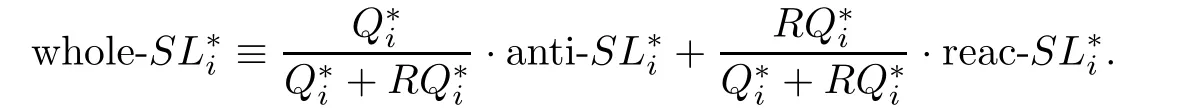
This model can solve a single-product newsboy problem.As we said before,we never sell only one product and the budget is always constrained.So we have to extend it to the budget constrained multi-product situation as follows:

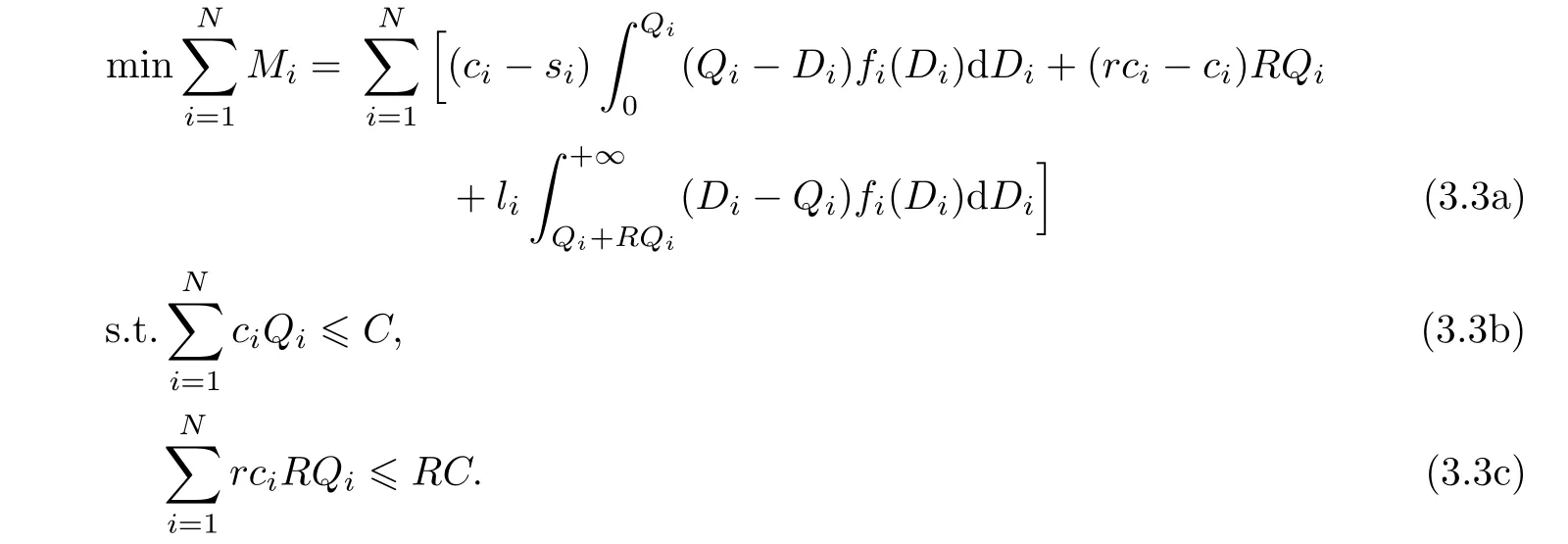
To solve it,we can use the procedure that deals with the constrained multi-product model.

Step 1.Relax the constraint

If we relax the constraint,the problem is the one that Chung and Flynn[4]have solved, i.e.,

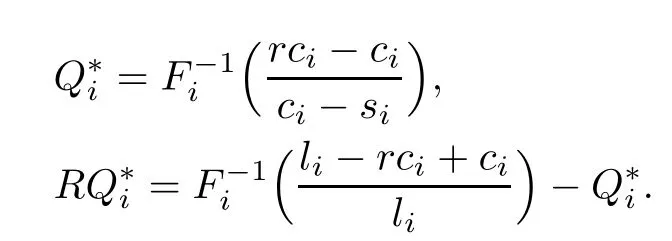
Step 2.Check up the constraint

Substituting Q∗iand RQ∗iin the budget constraints,we can find whether they are binding or not.If the constraint does not work,then Q∗iis RQ∗iand is the optimal solutions that we want.So the problem is solved.If the constraint works,then we go to Step 3.

Step 3.Lagrange multiplier procedure

The Lagrange function can be de fi ned as follows:

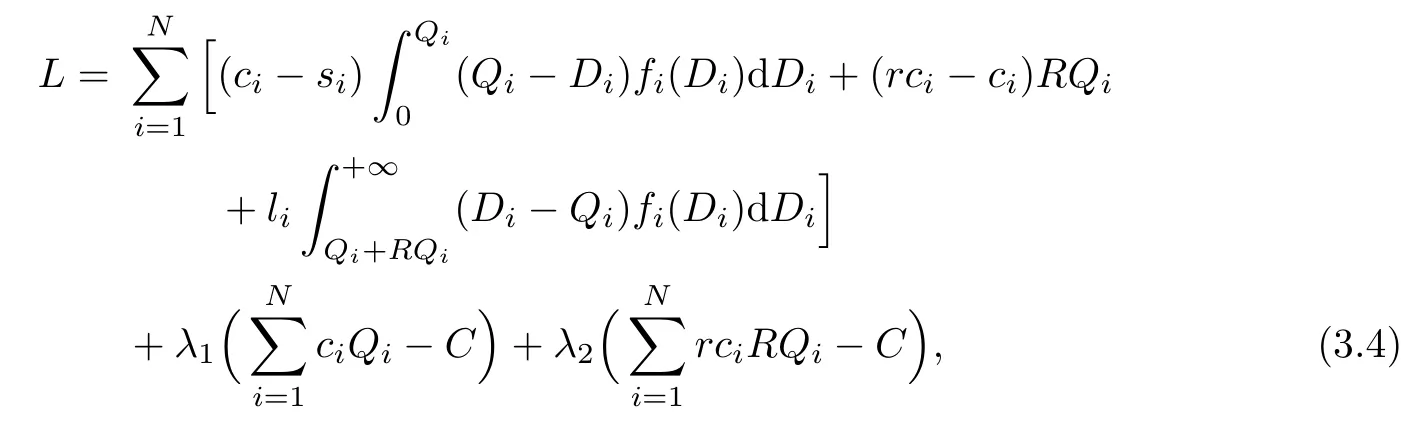
where λ1and λ2are Lagrange multipliers.

We can obtain

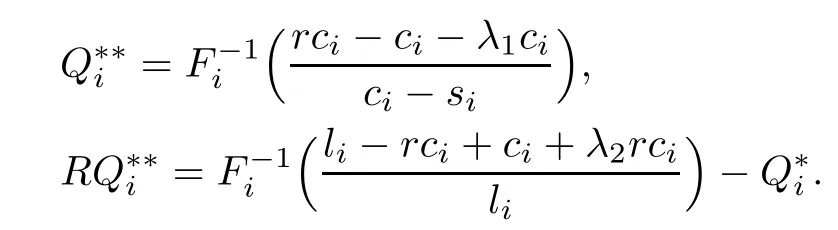
The values of the Lagrange multipliers λ1and λ2can be determined by solving the following nonlinear equations:

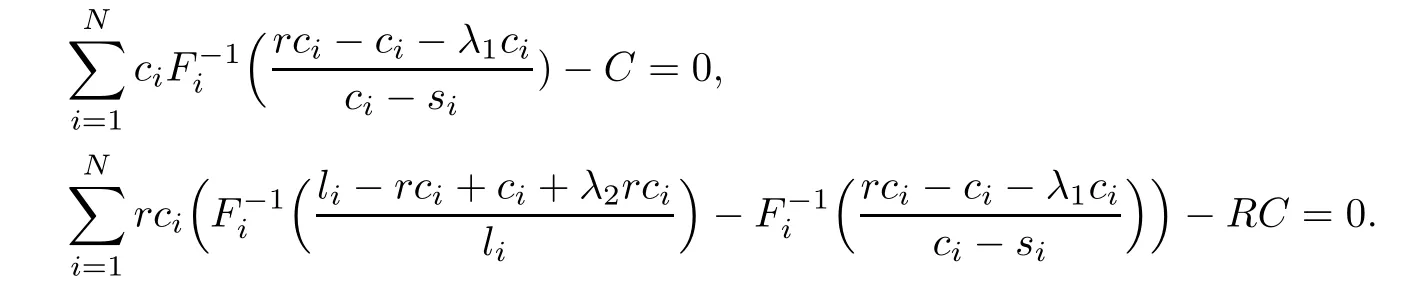
We can see that it is so hard to get the exact solutions of the problem.So we try to find a better method to solve the problem.As we know,it is a nonlinear programming problem. We can use the combined homotopy interior point method to our problem(see[8]).

We de fi ne

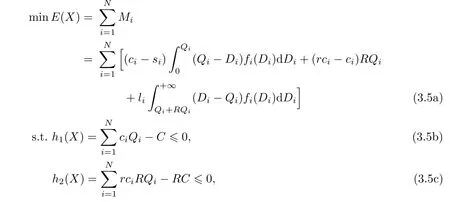
where

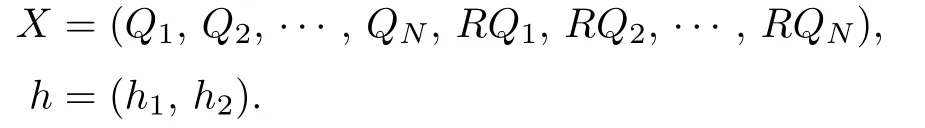
The Kuhn-Tucker point of(3.5a)–(3.5c)must satisfy

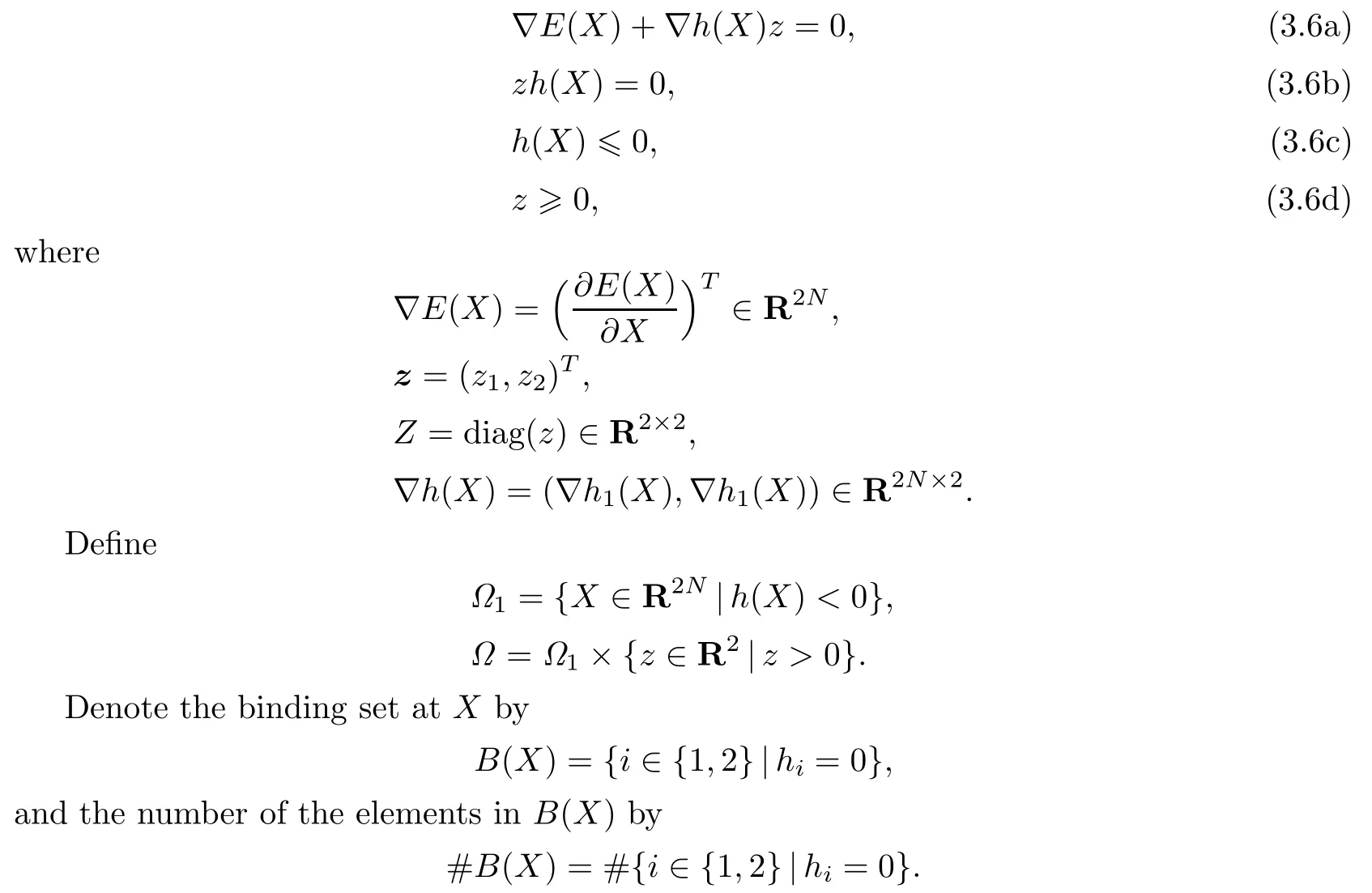
In our problem,the following three conditions are satis fi ed.

(C1)Ω1is nonempty and bounded;

To solve(3.6a)–(3.6d),we construct a homotopy as follows:

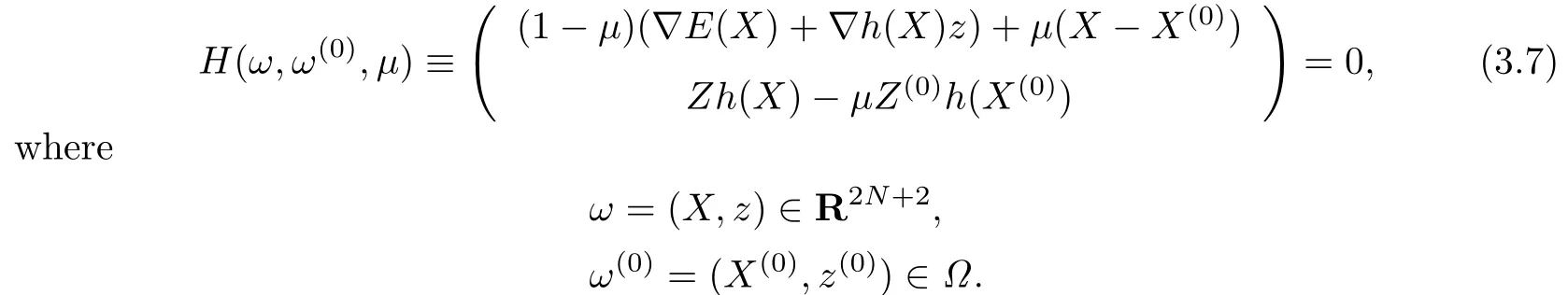
This is a combined homotopy and the corresponding algorithm is the combined homotopy interior point method.

Whenµ=1,the homotopy equation becomes

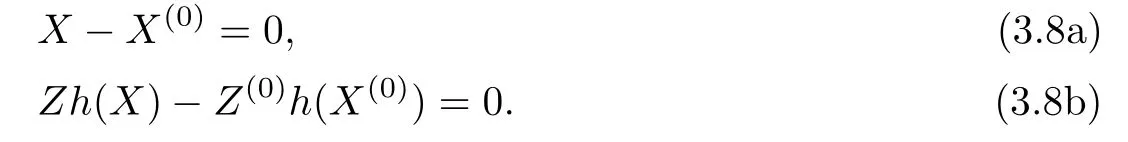
The solution of this equation is ω=ω(0).

Asµ=0,H(ω,ω(0),µ)=0 turns to the problem we considered.

For a given ω(0),write H(ω,ω(0),µ)as Hω(0)(ω,µ).The zero-point set of Hω(0)(ω,µ)is

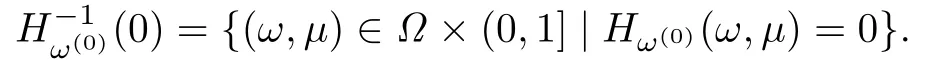
The following theorem shows the convergence of the method.

Theorem 3.1IfE(X),h1,h2are three times continuously differentiable functions,and the conditions(C1)–(C2)hold,then the problem has at least one solution.

For almost allω(0)∈Ω,the zero-point set ofH−1

ω(0)(0)of homotopy mapH(ω,ω(0),µ)contains a smooth curve Γω(0)⊂Ω×(0,1],which starts from(ω(0),1).Asµ→0,the limit setT×{0}⊂ ¯Ω×{0}of Γω(0)is nonempty,and every point inTis a solution of the problem. Speci fi cally,if the length of Γω(0)is finite and(ω∗,1)is the end point of Γω(0),thenω∗is a solution of the problem.

The proof is omitted(see[7]).

We can parameterizeΓω(0)with respect to s,

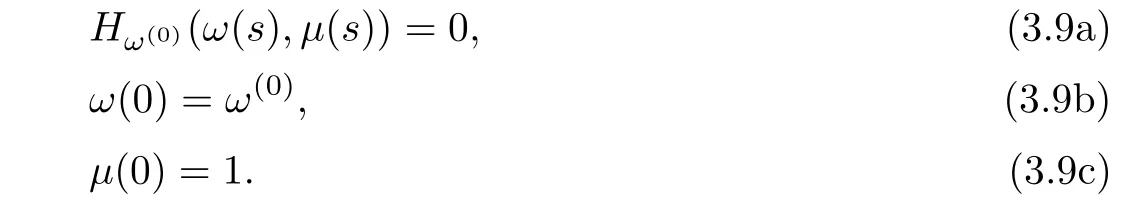
The homotopy pathΓω(0)is determined by the following initial value problem of an ordinary differential equation:

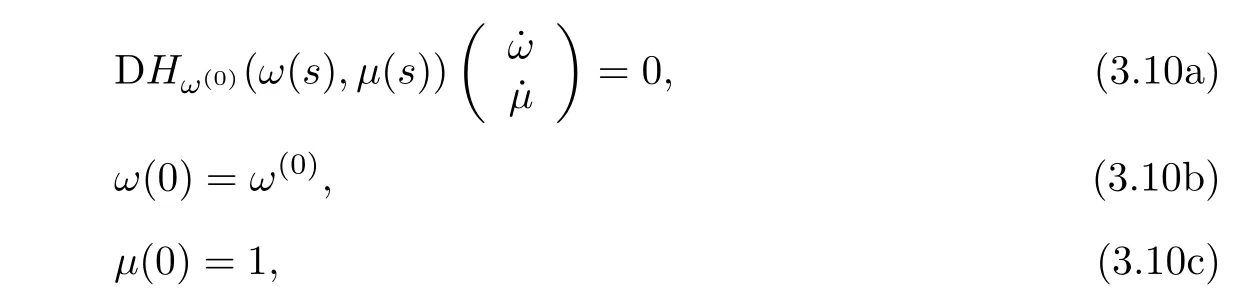
where“D”denotes the differential,i.e.,(3.10a)is the differential of(3.9a).

We give the flow chart to actualize the combined homotopy interior point method.It is the classical predictor-corrector procedure.

Step 1.Let(ω(0),µ(0))∈Ω×{1}be an initial point,h0＞0 be an initial steplength, ε1,ε2,ε3＞0 be small positive numbers and k=0.

Step 2.Compute the direction η(k)of the predictor step.Firstly,compute a unit tangent vector ξ(0)∈R2N+3.Secondly,determine the direction η(k)of the Step 1.

If the sign of the determinant

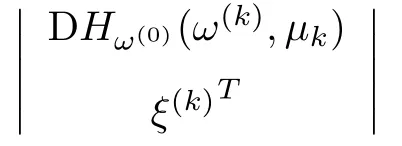
is(−1)2+1,then η(k)=ξ(k).

If the sign of the determinant is(−1)2,then η(k)=−ξ(k).

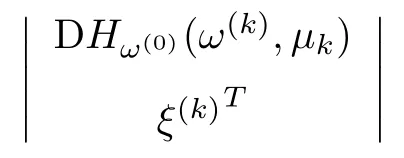
Step 3.Compute a corrector point(ω(k+1),µ(k+1)).One has

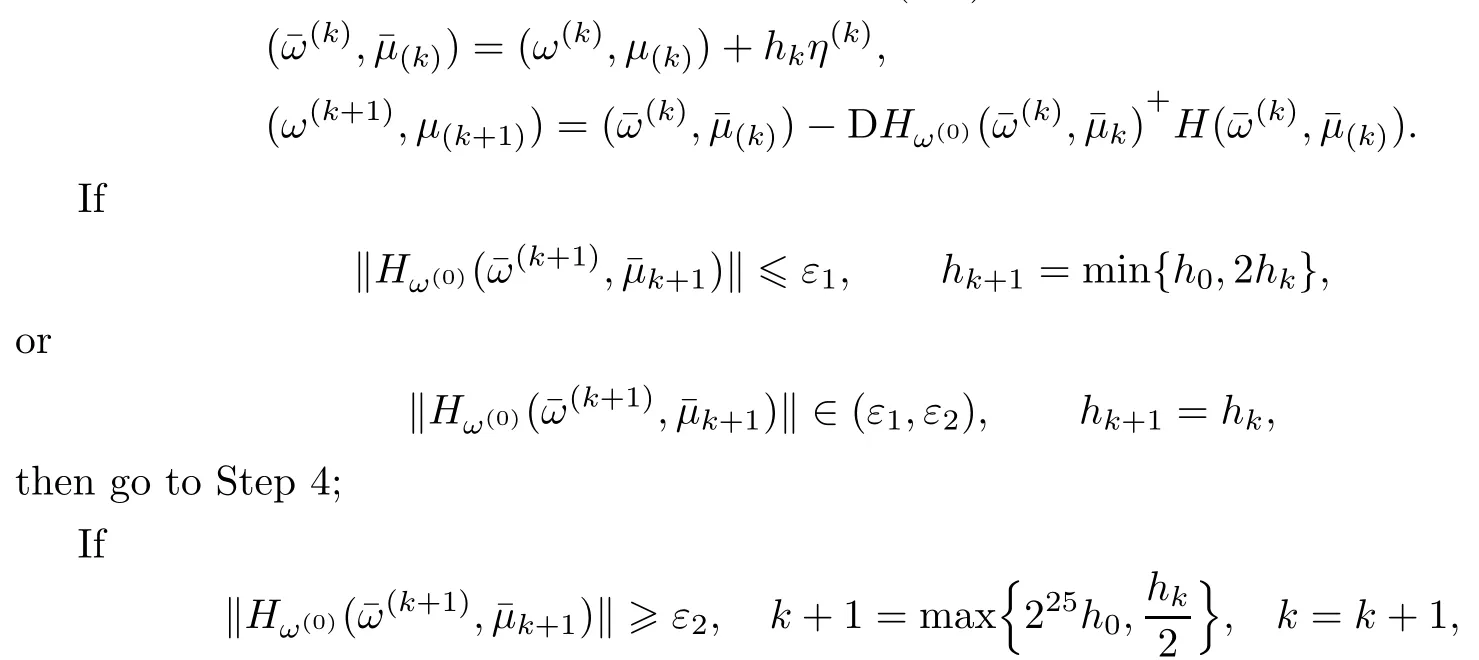
then go to Step 3;

Step 4.Ifµk+16 ε3,then stop.If not,set k=k+1,then go to Step 2.

In the procedure,we have

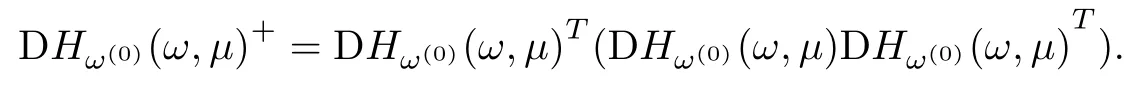
4 Numerical Example

In this section,a simple example is given.There are only two products in this problem.The cumulative demand function of both products is a normal distribution function.

The demand density function of each product is

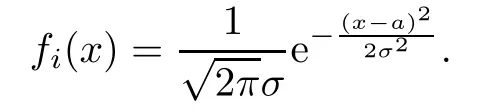
First,we use the classical method to solve the problem.Follow the Lagrange multiplier procedure.

Step 1.Relax the constraint

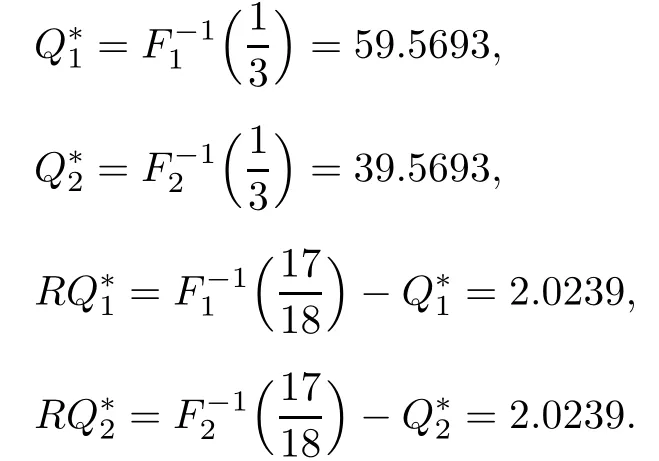
Step 2.Check up the constraint

Substitute Q∗iand RQ∗iinto the budget constraints,and we can find that they are binding.So we go to Step 3.

Step 3.Lagrange multiplier procedure

The Lagrange function can be introduced as follows:

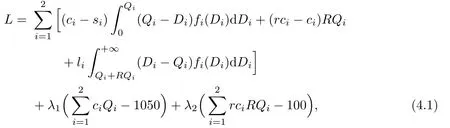
where λ1and λ2are Lagrange multipliers.

We can obtain

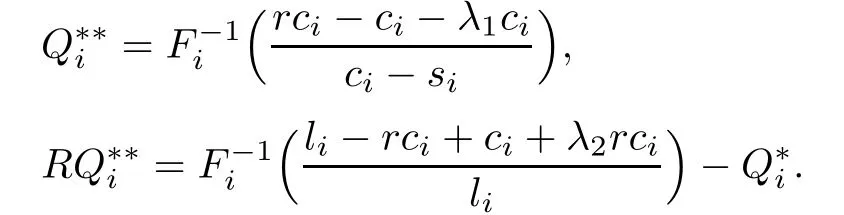
The values of the Lagrange multipliers λ1and λ2can be determined by solving the following non-linear equations:

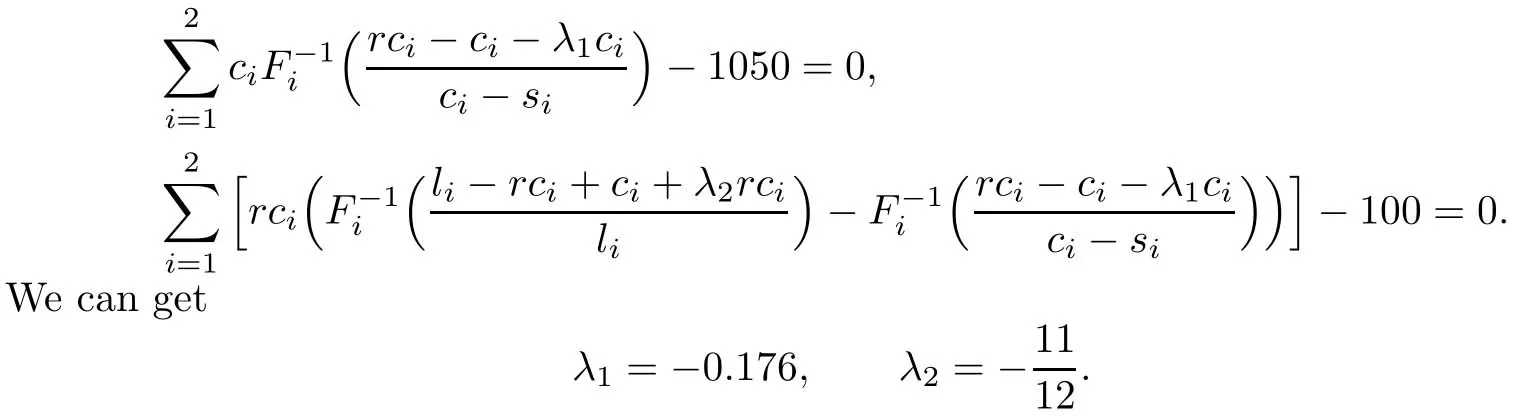
So the optimal order quantitiy for each product is

The optimal order quantity in a reactive production for each product is

We use the homotopy interior point method to deal with this problem.The optimal order quantity in a reactive production for each product is

It shows that the homotopy interior point method can give us the optimal order quantity in theory.Getting its inverse function is not an easy problem,so the homotopy method is more exact and efficient.

[1]Harris F W.How many parts to make at once.Oper.Res.,1999,38:947–950.

[2]Hadley G,Whitin T M.Analysis of Inventory Systems.Englewood Cli ff s.NJ:Prentice Hall, 1963.

[3]Khouja M.The single-period(news-vendor)problem:Literature review and suggestions for future research.Omega,Internat.J.Management Sci.,1999,27:537–553.

[4]Chung C,Flynn J.A newsboy problem with reactive production.Comput.Oper.Res.,2001, 28:751–765.

[5]Lau H,Lau A H.The multi-product multi-constraint newsboy problem:Applications,formulation and solution.J.Oper.Management,1995,13:153–162.

[6]Lau H,Lau A H.The newsstand problem:A capacitated multiple-product single-period inventory problem.European J.Oper.Res.,1996,94:29–42.

[7]Lin Z H,Li Y,Yu B.A combined homotopy interior point method for general nonlinear programming problems.Appl.Math.Comput.,1996,80:209–224.

[8]Cai L,Zhu X M,Li W J,Harris M S.Social network ties and resource acquisition:Evidence from China’s transitional economy,Internat.J.Business and Systems Research.2010,4:648–672.

Communicated by Li Yong

91F20,78M50

A

1674-5647(2012)02-0097-11

date:Nov.7,2007.

The NSF(70732005)of China.