Stability of Global Solution to Boltzmann-Enskog Equationwith External Force∗

JIANG ZHENG-LU,MA LI-JUNAND YAO ZHENG-AN

(1.Department of Mathematics,Sun Yat-Sen University,Guangzhou,510275)

(2.School of Mathematics,Hebei University of Technology,Tianjin,300401)

Stability of Global Solution to Boltzmann-Enskog Equation
with External Force∗

JIANG ZHENG-LU1,MA LI-JUN2AND YAO ZHENG-AN1

(1.Department of Mathematics,Sun Yat-Sen University,Guangzhou,510275)

(2.School of Mathematics,Hebei University of Technology,Tianjin,300401)

In the presence of external forces depending only on the time and space variables,the Boltzmann-Enskog equation formally conserves only the mass of the system,and its entropy functional is also nonincreasing.Corresponding to this type of equation,we first give some hypotheses of its bicharacteristic equations and then get some results about the stablity of its global solution with the help of two new Lyapunov functionals:one is to describe interactions between particles with different velocities and the other is to measure the L1distance between two mild solutions. The former Lyapunov functional yields the time-asymptotic convergence of global classical solutions to the collision free motion while the latter is applied into the verifi cation of the L1stability of global mild solutions to the Boltzmann-Enskog equation for a moderately or highly dense gas in the in fl uence of external forces.

Boltzmann-Enskog equation,global solution,stability,Lyapunov functional

1 Introduction

We are interested in the time-asymptotic behaviour and the Lyapunov stability of the global classical solution to the Enskog equation for a moderately or highly dense gas in the in fl uence of external forces.As the generalization of the Boltzmann equation,the Enskog equation is a model first proposed by Enskog[1]in 1922 for a description of the dynamical behavior of the density of a moderately or highly dense gas.This is because the Boltzmann equation is no longer suitable for gases with high-density e ff ects although it models dilute gases successfully.The Enskog equation is a partial differential integral equation of the hyperbolic type.There are some different versions of the Enskog equation in order that they formally satisfy some properties,such as entropy bound and consistence with irreversible thermodynamics(see [2–3]).We now take into account the so-called Boltzmann-Enskog equation,in the presence of external forces E(t,x)depending on the time and space variables t∈R+and x∈R3,as follows:

for a one-particle distribution function f=f(t,x,v)that depends on time t∈R+,the position x∈R3and the velocity v∈R3,where Q is the collision operator whose form will be addressed below.Here and throughout this paper,R+represents the positive side of the real axis including its origin andR3denotes the three-dimensional Euclidean space.

The collision operator Q is expressed by the di ff erence between the gain and loss terms respectively,and de fi ned by

In(1.2)-(1.3),S2+={ω∈S2:ω·(v−w)≥0}is a subset of a unit sphere surface S2inR3,a is a diameter of hard sphere,ω is a unit vector along the line passing through the centers of the spheres at their interaction,(v′,w′)are velocities after collision of two particles having precollisional velocities(v,w),and

is the collision kernel.

The Boltzmann-Enskog equation(1.1)is a modi fi cation of Enskog’s original work mentioned above and obeys only the conservation laws of mass in the presence of external forces.It is worth mentioning that the equation(1.1)still obeys the conservation laws of mass,momentum and energy under the assumption that E(t,x)=0,that is,in the absence of external forces(see[4]).

As for the Boltzmann equation,two colliding particles obey the conservation laws of both kinetic momentum and energy as follows:

This results in their velocity relations

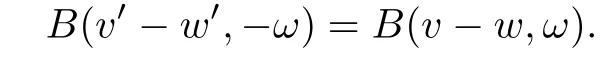
The two postcollisional velocities given by(1.5)also have another expression as follows(see [5–6]):

There is a vast literature on the global existence and uniqueness of the solutions to the initial value problem for the Boltzmann and the Enskog equations without external forces. In the absence of external forces,a theorem about the existence and uniqueness of global solution was first given by Ukai[7]for the Boltzmann equation,and another global existence and uniqueness result was then shown by Illner and Shinbrot[8]about the solutions to the initial value problem for the Boltzmann equation with small initial data in the in finite vacuum,and after that,a global solution existence proof was given by DiPerna and Lions[9]for the Boltzmann equation with large data,but up to now,one cannot know whether the solution to the problem is unique or not.For the Enskog equation without external forces, one may find some solution existence results,together with the L1stability of solutions, which were given by Cercignani[10].At that time,with an analysis of the well-posedness of the initial value problem in unbounded domains,some global existence and uniqueness theorems were obtained by Toscani and Bellomo[11]about the solutions to the Enskog equation in the absence of external forces for small initial data with suitable decay to zero at in fi nity in the phase space,and the asymptotic stability of the solutions and the in fl uence of the external field was also discussed in this reference.After that,a global existence and uniqueness proof was given by Polewczak[3]for the Enskog equation with near-vaccum data and another one shown by Arkeryd[2]for the present Boltzmann-Enskog equation with large data.The time-asymptotic behaviour of solutions in the weighted L∞was also provided by Polewczak[3,12]for the Enskog equation in the absence of external forces.

Two Lyapunov functionals were constructed by Ha[13]to show both the L1stability and the time-asymptotic behaviour for global classical solutions to the Boltzmann-Enskog equation without external forces.Recently,Jiang[14]found that two key inequalities do not hold mathematically in the proof given by Ha(see(3.1)and(3.2)in[13]),and then built two different Lyapunov functionals and showed their time-decay properties.When we use the new functionals to study the stability and the asymptotic behaviour,we can solve the problem of the inequalities mentioned above.The time-decay properties of our functionals not only yield the time-asymptotic behaviour in the L1norm but also recover the L1stability for global classical solutions to the Boltzmann-Enskog equation without external forces.On the other hand,in the case of having external forces in in finite vacuum,a global existence and uniqueness theorem of mild solutions was given by Duanet al.[5]for the Boltzmann equation,and a similar result was shown by Jiang[14]for the Boltzmann-Enskog equation. Now there is no yet this result about both the time-asymptotic behaviour and the stability of solutions to the Boltzmann-Enskog equation in the presence of external forces.The aim of this paper is to build new functionals to show this type of result in the case of the Boltzmann-Enskog equation with external forces.

The rest of this paper is arranged as follows.In Section 2 some properties of the collision operator Q of the Boltzmann-Enskog equation(1.1)are introduced including both the entropy identity and the nonincreasing property of the system entropy functional.In Section 3 some hypotheses of the external forces are then given for the Boltzmann-Enskog equation(1.1).New functionals are constructed and the time-asymptotic behaviour of a small family of solutions to the Boltzmann-Enskog equation(1.1)with external forces is given in Section 4.different functionals are de fi ned and the Lyapunov stability of solution to the Boltzmann-Enskog equation with external forces is fi nally shown in Section 5.

2 The Conservation of Mass and the Entropy Functional

In this section,we first prove a property of the collision operator Q introduced above,in order to show formally the conservation law of mass for the Boltzmann-Enskog equation (1.1)in the presence of external forces,and then we derive the entropy identity to get the nonincreasing property of the system entropy functional.

Note that

For the collision operator Q of the Boltzmann-Enskog equation(1.1)with(1.2)and(1.3) we give the following lemma.

Lemma 2.1Suppose thatQ=Q+−Q−is a collisional operator as de fi ned by(1.2)and(1.3).Letψ=ψ(x,v)andf=f(x,v)be two measurable functions onR3×R3.IfψQ±(f)∈L1(R3×R3),then

Let us first consider the loss integral Il.We proceed one step by exchanging v and w and replacing ω with−ω in the integral on the right hand side of(2.4).Then we replace x with x+aω and use(2.4).Thus we get

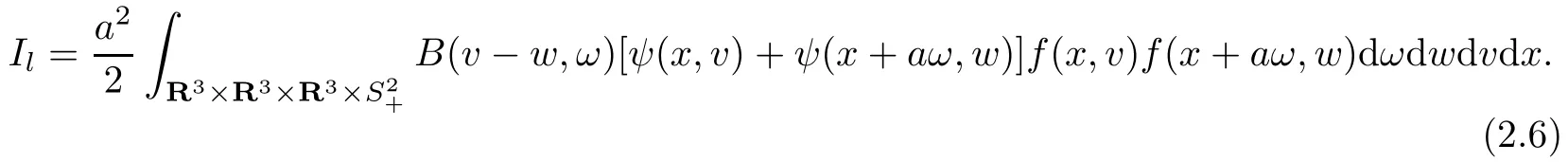
The gain integral Igwill be considered below.By using the properties that

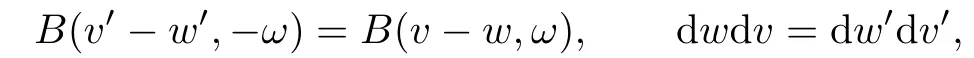
we first rechange(2.3)as an integral with respect to the variables of ω,w′,v′and x.Then we exchange v and v′,w and w′,and replace ω with−ω.Finally,by using the same kind of changes of the loss integral Il,we can get

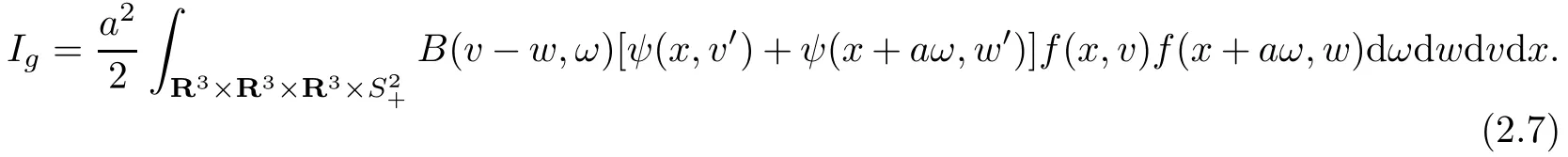
Inserting(2.6)and(2.7)into(2.5)gives(2.1).

Similarly,we can get(2.2).

We usually call HB(t)the Boltzmann entropy functional.It has the following property:Theorem 2.1Put

whereHB(t)andI(t)are de fi ned as follows:

Assume thatf=f(t,x,v)is a nonnegative classical solution to the Boltzmann-Enskog equation(1.1)inL1(R3×R3),and bothQ±(f)andln(f)Q±(f)belong toL1(R3×R3).

By integrating over the variable x on the right hand side of(2.10),Lemma 2.1 and the fact that

(2.12)is also called the entropy indentity.Since lnx≤x−1 for x＞0,the estimation of the integral on the right hand side of the entropy indentity(2.12)reads as

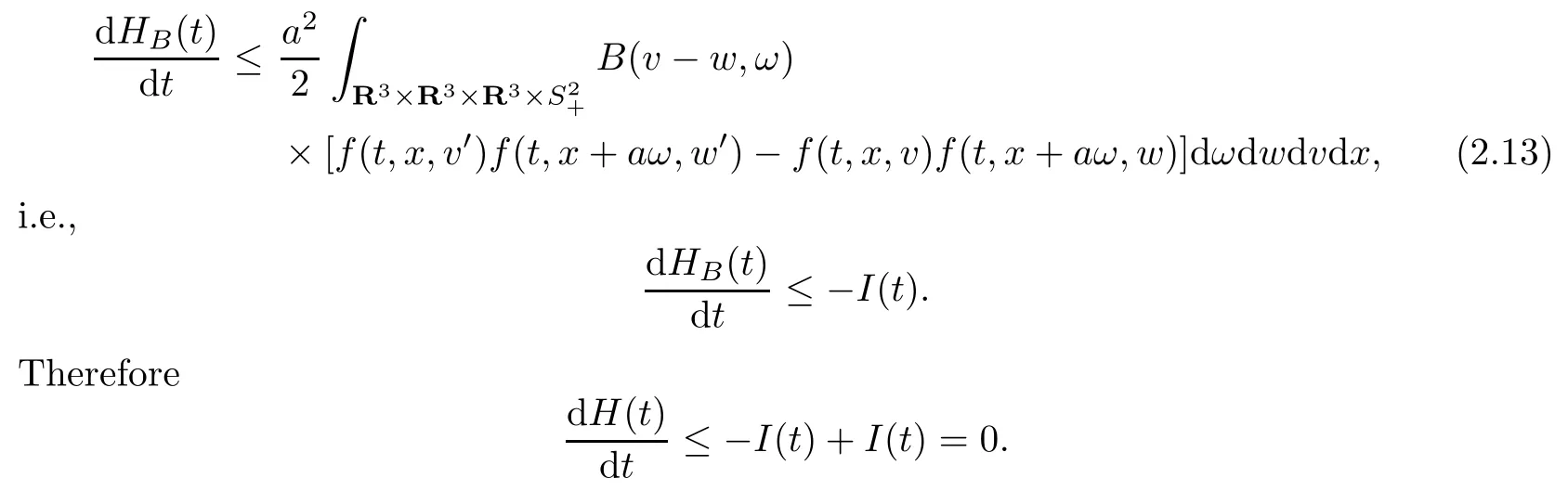
The proof of this theorem is finished.

We usually call H(t)in Theorem 2.1 the entropy functional of the system.Theorem 2.1 shows that the entropy functional of the system is nonincreasing.

3 Hypotheses of External Forces

In this section some hypotheses of the external forces are made and a representation of the mild solution is given for the Boltzmann-Enskog equation(1.1).

Let us begin with the bicharacteristic equations of the Boltzmann-Enskog eqaution(1.1):

Suppose that such a vector-value force function E(t,x)allows the above system(3.1)to have a global-in-time smooth solution denoted by

for any fixed(t,x,v)∈R+×R3×R3,and that there exist two functions αi(s;t,x,v) (i=1,2)such that the solution(3.2)satis fies the following conditions:

for any s∈R+and(ξ,η)∈R3×R3with any point(t,x,v) fixed inR+×R3×R3,where α0,d0and e0are positive constants independent of s and(t,x,v),and(s;t,x,v)(i=1,2) represent the derivative with respect to s.

We now give a representation of the mild solution to the Boltzmann-Enskog equation. Let us first introduce an operator U(s)de fi ned as follows:

A function f(t,x,v)is called a global mild solution to the Boltzmann-Enskog equation (1.1)if f(t,x,v)satis fies(3.10)for almost every(t,x,v)∈R+×R3×R3.

By(1.7)and(1.8),U(s)Q(f)(t,x,v)can be rewritten as the di ff erence between the gain and loss terms of two other forms:

Remark 3.1We construct a subset M of a Banach space C(R+×R3×R3),which has the property that every element f=f(s,x,v)∈M if and only if there exists a positive constant c such that f satis fies

for any fixed p and q in(0,+∞).It follows that M is a Banach space when it is equipped with a norm of the following form:

The initial data f0≡f(0,x,v)is bounded in L1(R3×R3).This implies that the total mass is finite.This requires that the mean free path is sufficiently large if the finite total mass is sufficiently small(see[5]).This is exactly the requirement on the Boltzmann-Enskog equation with external forces in in finite vacuum,which is similar to one considered by Illner and Shinbrot[8]for the Boltzmann equation.It is worth mentioning that there are many different classes of functions which can be taken as the choice of h(X(0;t,x,v))and m(V(0;t,x,v))(see[5–6]).Suppose that the conditions(3.2)–(3.7)hold and that h(x)and m(v)are the same as in(3.15).It can be then known from[14]that the Boltzmann-Enskog equation(1.1)has a unique non-negative global mild solution f=f(t,x,v)∈M through a non-negative initial data f0=f0(x,v)when

is sufficiently small.

4 Asymptotic Behaviour

In this section we build two new functionals and study their properties,and then show the time-asymptotic behaviour of a class of solutions to the Boltzmann-Enskog equation(1.1).

Let us begin with two new functionals D=D++D−and F=F++F−,which are de fi ned as follows:

where for clarity,X(s)and V(s)represent X(s;t,x,v)and V(s;t,x,v),respectively,from which the initial variables(t,x,v)are suppressed.Obviously,by(3.13)and(3.14),we know that

For a special class of solutions f to the Boltzmann-Enskog equation,D[f](s)describes interactions between particles with various velocities.It can be found below that the timedecay property of D[f](s)for a special class of solutions f to the Boltzmann-Enskog equation leads directly to the time-asymptotic behaviour of these solutions in L1(R3×R3)and so D

is called Lyapunov functional.To estimate the time decay of D[f](s),we first have to show the following lemma.

Lemma 4.1[14]LetF(x)be an integrable function onR3andva vector inR3.Assume thatS2+={ω|v·ω≥0,ω∈S2}whereS2is a unit sphere surface inR3.Then

Combining De fi nition(4.1)and Lemma 4.1,we can easily deduce that

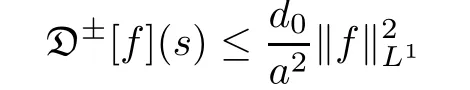
for a class of integrable function f=f(t,x,v).Furthermore,we also obtain a similar timedecay property of D[f](s)to that shown by Jiang[14]as follows.

Theorem 4.1LetDandFbe de fi ned by(4.1)and(4.2).Assume thatf=f(t,x,v)is a nonnegative classical solution to the Boltzmann-Enskog equation(1.1)with(1.2)and(1.3)through an initial datumf0=f0(x,v),and that bothfandfQ±(f)belong toL1(R3×R3).Giving the hypothesis(3.8)of the external forcesE(t,x),and assuming the diametera＞0,then we have

Proof.The proof of this theorem is similar to that of Jiang[14].

By Theorem 4.1,we then get

Theorem 4.2Put

Assume thatf=f(t,x,v)is a nonnegative classical solution to the Boltzmann-Enskog equation(1.1)with(1.2)and(1.3)through an initial datumf0=f0(x,v)satisfying

and that bothfandfQ±(f)belong toL1(R3×R3).Giving the hypothesis(3.8)of the external forcesE(t,x),and assuming the diametera＞0,thenf(t,x,v)converges inL1(R3×R3)tof∞(t,x,v)astgoes to+∞.

Proof.By Theorem 4.1,we know that

where D[f](s)and F[f](s)are the same as in Lemma 4.1.It follows that

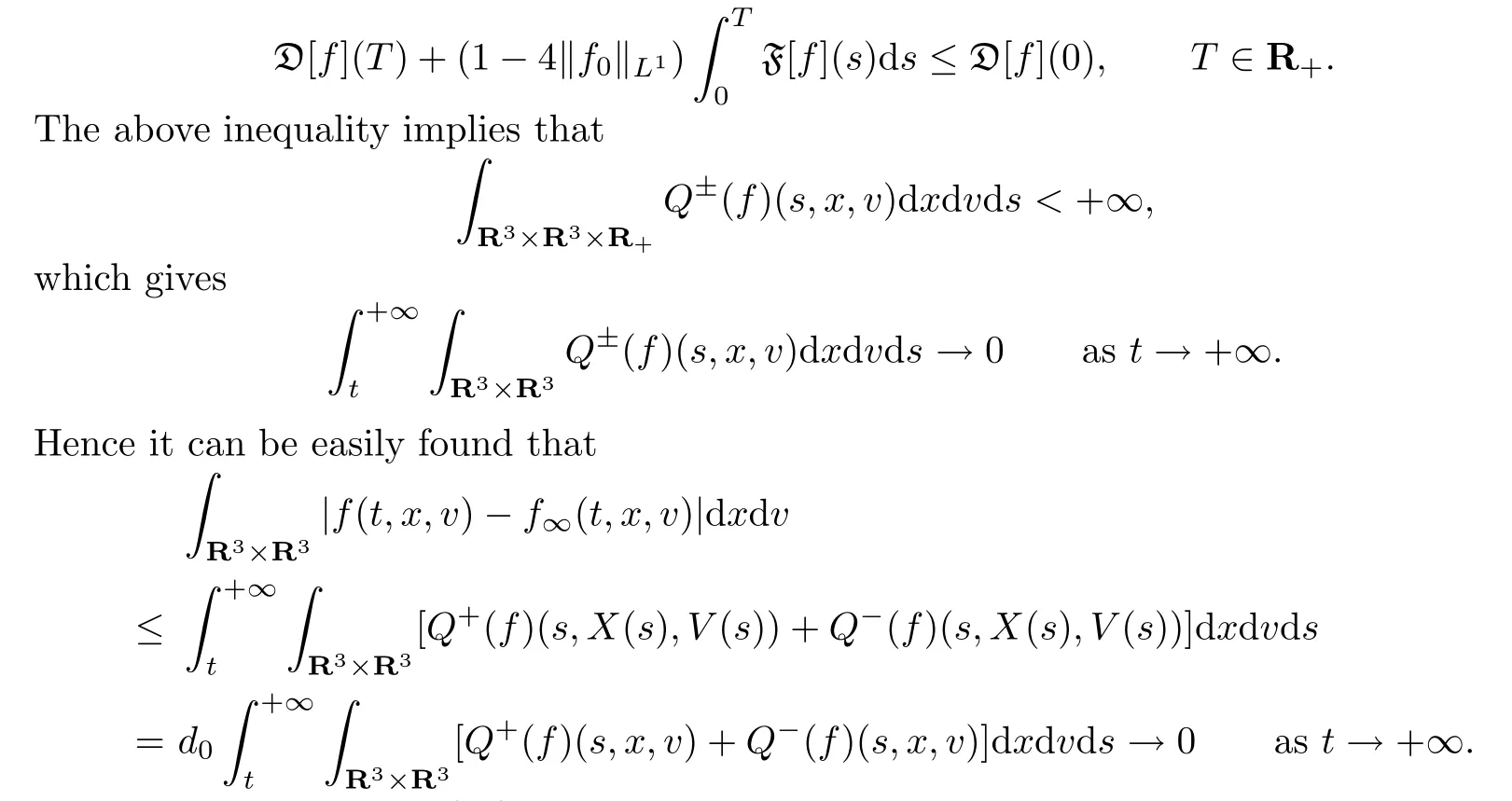
This completes our proof of Theorem 4.2.

Remark 4.2In Theorem 4.2 the time-asymptotic behaviour of a class of solutions to the Boltzmann-Enskog equation is in fact the time-asymptotic convergence of this type of solutions in the L1norm to the free motion as t trends to in fi nity.The time-asymptotic convergence in the L∞norm for the Boltzmann-Enskog equation in the presence of external forces can be also shown by using the same method as given by Polewczak[3]for the Enskog equation in the absence of external forces.

5 L1Stability

In this section some new functionals are constructed for the L1stability of global classical solutions to the Boltzmann-Enskog equation(1.1)with(1.2)and(1.3).One of them is a Lyapunov functional and it is equivalent to the L1distance functional.The time-decay property of the Lyapunov functional is also shown for the L1stability.

Let us begin with constructing two functionals L[f,g](s)and Fd[f,g](s)as follows. L[f,g](s)is de fi ned by

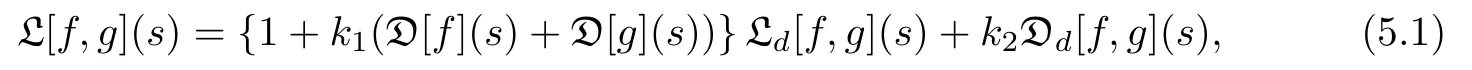
where k1and k2are positive constants to be determined later,D is the same as given by (4.1),Ldis denoted by

This functional L is here called a Lyapunov functional.

We first have the following property of the equivalence between the Lyapunov functional and L1distance functionals L and Ld.

Lemma 5.1LetLandLdbe de fi ned by(5.1)and(5.2),respectively.Suppose that the hypothesis(3.8)of the external forcesE(t,x)holds.Assume that

本组20例患者随访1年以上，末次随访时，所有患者无疼痛，关节活动明显改善15例，关节活动部分改善3例，无改善的2例。

are two nonnegative classical solutions to the Boltzmann-Enskog equation(1.1)with(1.2)and(1.3)through initial dataf0=f0(x,v)andg0=g0(x,v),respectively,and that all the functionsf,g,fQ±(f)andgQ±(g)are elements inL1(R3×R3).Then

where

and by(3.8)and Lemma 4.1 it can be found that W(s,X(s),V(s))is bounded by the L1norms of f0and g0as follows:

(5.5)thus follows.Our proof of this lemma hence ends up.

For a class of solutions f=f(t,x,v)and g=g(t,x,v)to the Boltzmann-Enskog equation (1.1)with(1.2)and(1.3),the time-decay properties of the two functionals Dd[f,g](s)and Ld[f,g](s)can be also obtained as follows.

Lemma 5.2LetLandLdbe de fi ned by(5.1)and(5.2),respectively.Suppose that the hypothesis(3.8)of the external forcesE(t,x)holds.Assume thatf=f(t,x,v)andg= g(t,x,v)are two nonnegative classical solutions to the Boltzmann-Enskog equation(1.1)with(1.2)and(1.3)through initial dataf0=f0(x,v)andg0=g0(x,v)respectively,and that all the functionsf,g,fQ±(f)andgQ±(g)are elements inL1(R3×R3).Then

It can be further shown that the functional L has the following time-decay property similar to that shown by Ha(see Theorem 1.4 in[13]).

Theorem 5.1LetLandFdbe de fi ned by(5.1)and(5.4),respectively.Suppose that the hypothesis(3.8)of the external forcesE(t,x)holds and that the diametera＞0.Assume thatf=f(t,x,v)andg=g(t,x,v)are two nonnegative classical solutions to the Boltzmann-Enskog equation(1.1)with(1.2)and(1.3)through initial dataf0=f0(x,v)andg0=g0(x,v)satisfyingrespectively,and that all thefunctionsf,g,fQ±(f)andgQ±(g)are elements inL1(R3×R3).Then there exists a positive constantsuch that

for anys∈R+,whereCis a positive constant independent ofs.

Proof.Similarly to the proof of Ha(see Theorem 1.4 in[13]).

By Theorem 5.1,we further have

Theorem 5.2Suppose that the hypothesis(3.8)of the external forcesE(t,x)holds and that the diametera＞0.Assume that

are two nonnegative classical solutions to the Boltzmann-Enskog equation(1.1)with(1.2)and(1.3)through initial dataf0=f0(x,v)andg0=g0(x,v)satisfying

respectively,and all the functionsf,g,fQ±(f)andgQ±(g)are elements inL1(R3×R3).ThenZZ

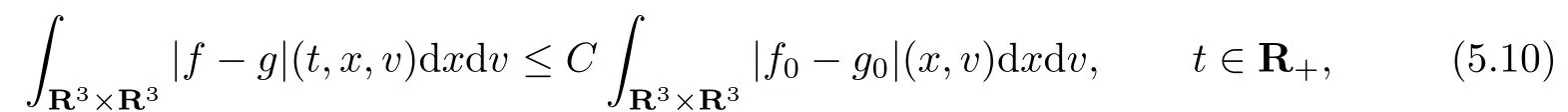
whereCis a positive constant independent oft.

[1]Enskog D.Kinetiche Theorie der W`armeleitung,Reibung und Selbstdi ff usion in gewissen werdichteten Gasen und Flubigkeiten.Kungl.Sv.Vetenskapsakademiens Handl,1922,63: 3–44,English Transl.in Brush S G,Kinetic Theory.vol 3.New York:Pergamon,1972.

[2]Arkeryd L.On the Enskog equation with large initial data.SIAM J.Math.Anal.,1990,21: 631–646.

[3]Polewczak J.Global existence and asymptotic behavior for the nonlinear Enskog equation.SIAM J.Appl.Math.,1989,49:952–959.

[4]Polewczak J.On some open problems in the revised Enskog equation for dense gases.In Proceedings“WASCOM 99”10th Conference on Waves and Stability in Continuous Media, Vulcano(Eolie Islands),Italy,June 7–12,1999.In:Ciancio V,Donato A,Oliveri F,Rionero S.London:World Scienti fi c Publishing,2001:382–396.

[5]Duan R,Yang T,Zhu C.Global existence to Boltzmann equation with external force in in finite vacuum.J.Math.Phys.,2005,46:053307.

[6]Guo Y.The Vlasov-Poisson-Bolzmann system near vacuum.Comm.Math.Phys.,2001,218: 293–313.

[7]Ukai S.Les solutions globales de l’quation de Boltzmann dans l’espace tout entier et dans le demi-espace,C.R.Acad.Sci.Paris Sr.A/B,1976,282(6):A317-A320.

[8]Illner R,Shinbrot M.The Boltzmann equation,global existence for a rare gas in an in finite vacuum.Comm.Math.Phys.,1984,95:217–226.

[9]DiPerna R J,Lions P L.On the Cauchy problem for Boltzmann equations:Global existence and weak stability.Ann.Math.,1989,130:321–366.

[10]Cercignani C.Existence of global solutions for the space inhomogeneous Enskog equation.Transport Theory Statist.Phys.,1987,16:213–221.

[11]Toscani G,Bellomo N.The Enskog-Boltzmann equation in the whole space R3:Some global existence,uniqueness and stability results.Comput.Math.Appl.,1987,13:851–859.

[12]Polewczak J.Global existence in L1for the modi fi ed nonlinear Enskog equation in R3.J. Statist.Phys.,1989,56:157–173.

[13]Ha S.Lyapunov functionals for the Enskog-Boltzmann equation.Indiana Univ.Math.J.,2005, 54:997–1014.

[14]Jiang Z.Global solution to Enskog equation with external force in in finite vacuum.Chinese J.Contemp.Math.,2009,30:49–62.

Communicated by Yin Jing-xue

76P05,35Q75

A

1674-5647(2012)02-0108-13

date:March 3,2009.

The NSF(11171356)of China and the Grant(09LGTY45)of Sun Yat-Sen University.