基于参数化模型优化的喷氨格栅设计方法研究
李 娜,卢作基,秦翠娟
(中环(中国)工程有限公司,江苏南京 210008)
基于参数化模型优化的喷氨格栅设计方法研究
李 娜,卢作基,秦翠娟
(中环(中国)工程有限公司,江苏南京 210008)
从喷氨格栅工程设计要求出发,结合数值模拟分析、代理模型技术以及优化设计方法,提出了一套基于参数化模型优化的喷氨格栅设计方法和流程。该方法从工程设计要求的分析入手,根据喷氨格栅几何参数对喷氨特性的影响特点和规律,建立参数化设计数学模型,并通过优化计算最终获得喷氨格栅的最优设计。另外,通过实例计算验证了该设计方法在SCR脱硝系统喷氨格栅设计中的适用性。
喷氨格栅;参数化模型;数值计算;代理模型;优化设计
0 引言
选择性催化还原法烟气脱硝(Selective Catalytic Reduction,SCR)是在催化剂作用下,以氨为还原剂将烟气中氮氧化物分解成氮气与水,其氮氧化物脱除效率高,适应当前环境保护要求,因而得到了电力行业高度重视和广泛应用[1-5]。在 SCR烟气脱硝系统中,氨气必须与烟气充分而均匀的混合才能确保其和反应物(烟气中的氮氧化物)充分结合,而一般国内燃煤电厂氨/烟气的流量比约为 1/1000量级,在如此悬殊的比例和超大烟气流量下实现氨/烟气快速均匀混合是一项挑战。对此,优良的喷氨系统起到了重要作用。
针对SCR烟气脱硝系统内喷氨强化掺混问题,国外进行了大量研究并提出了一些新概念喷氨强化掺混技术,例如:利用先进的整流/导流结构设计实现烟气速度场分布均匀的同时也完成氨与烟气掺混均布[6-7]、利用涡街和旋流特征促进气流掺混的新概念喷氨装置以及多点多角度喷射结构等[8-10]。文献[11]、[12]还研究应用现代控制理论方法来优化类似的喷氨控制系统。
目前国内外较多采用喷氨格栅进行多点喷射,使氨广泛分布在整个烟道截面上。喷氨格栅的设计是一项复杂且困难的工作,其技术上的困难之一是喷氨格栅的几何设计变量较多,包括喷氨管管束布置,喷氨孔排布,喷氨孔孔径及喷氨角度等,其均对喷氨效果有直接影响,而且这些几何因素之间也存在一定的相互制约,因此,对于喷氨格栅而言,很难通过对某一个变量的设计即达到理想喷氨效果,而需要对若干几何变量进行综合分析,以期实现喷氨格栅的最优设计[13-14];困难之二在于必需根据实际烟气环境,对烟道及反应器内的喷氨及其与烟气掺混过程进行反复计算,计算技术复杂、计算量庞大。从现有文献来看,国内主要是一些大学在SCR烟气脱硝喷氨技术方面开展了相关研究工作,但大都是针对喷氨格栅的影响因素及其影响规律进行一定的探讨[13-18],缺少一种系统的喷氨格栅设计方法。本文即从喷氨格栅工程设计要求出发,结合代理模型技术和优化方法[19-21],提出了一种基于参数化模型优化的喷氨格栅设计方法和流程。并通过实例计算验证了该设计方法在SCR脱硝系统喷氨格栅设计中的适用性。
1 基于参数化模型优化的喷氨格栅设计
喷氨格栅设计应当从工程设计要求的分析入手,根据喷氨格栅几何参数对喷氨特性的影响特点和规律,确定初始设计方案。初步选定对喷氨特性有重要影响的关键几何参数,建立喷氨格栅的参数化数学模型。结合三维粘性流场数值分析及优化计算,从而得到喷氨格栅的初步设计结果。然后,对初步设计结果进行计算和评估,如果能够满足设计要求,则该喷氨格栅的设计是成功的,否则修改设计方案,调整几何参数取值,重新进行优化设计,直至设计出满足设计要求的喷氨格栅。
1.1 喷氨格栅设计要求分析与初始方案设计
喷氨格栅作为SCR脱硝系统的重要部件,承担着将氨广泛喷射在烟道中,一方面要让每个喷氨孔的喷氨能够在设计的混合段长度内,与该喷氨孔对应区域内的烟气充分均匀混合;另一方面要使整个烟道内的氨浓度与烟气中氮氧化物浓度分布尽量匹配。因此,SCR脱硝系统喷氨格栅结构设计的主要目标是在烟气设计点流速条件下,通过对关键几何参数的优化设计,使得氨与烟气能够在设计的混合段长度内充分均匀混合。另外,在实际工作过程中,如果烟道内烟气速度场及烟气中氮氧化物浓度场分布不均,则针对烟气浓度场分布情况对喷氨管内氨流量进行分区域控制,以实现氨与烟气中氮氧化物浓度分布的匹配。
图1给出了典型SCR脱硝系统喷氨格栅示意,由图可见,喷氨格栅由以一定间距布置的喷氨管管束构成,喷氨管上排布着若干喷氨孔。一般情况下,为促进氨与烟气的迅速掺混,喷氨管上的喷氨孔对开,且喷氨方向垂直于烟气流方向。如图1所示,喷氨格栅的几何设计变量主要包括:喷氨截面的宽W与高H,喷氨管间距Ll,喷氨管上喷氨孔间距Lh,以及喷氨孔直径D。

图1 喷氨格栅示意
实际工程中,烟气流量及氮氧化物含量已知,可推算出所需氨气流量m,另外,烟道截面是基本确定的,即喷氨截面的宽W与高H已知,那么,喷氨孔数量N约为:
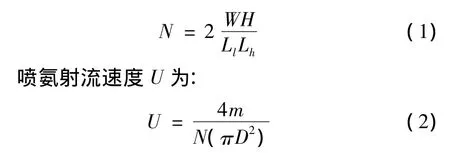
根据对喷氨格栅设计要求的分析,可基本确定其初始设计方案:
(1)根据喷氨格栅几何参数对喷氨特性的影响特点和规律,初步选定对喷氨特性有重要影响的关键几何参数,建立喷氨格栅的参数化模型。
(2)确定混合段长度Ld,以及经混合段后氨与烟气的掺混程度,以浓度偏差δ表示。浓度偏差δ的定义为:

式中:Ci是测试点的浓度值,n为测试点的个数为所有测试点浓度值的数学平均值。
(3)烟道几何尺寸及喷氨射流速度将作为喷氨格栅几何参数设计的约束,根据工程实际情况选定。
1.2 喷氨格栅参数化模型优化设计
对于图1所示的喷氨格栅,在假设烟道尺寸及烟气环境一定的前提下,喷氨射流经混合段长度后,氨气的浓度偏差主要由喷氨格栅的几何参数、氨气性质以及氨气射流条件等因素共同决定。假设它们之间存在如下函数关系:

式中:C为氨气浓度,P和T分别为氨气射流出口压力及温度,g1,g2,…,gn为描述喷氨格栅的n个几何参数。在设计点条件下,氨气性质及其射流条件是一定的,则浓度偏差函数关系(4)可简化为:
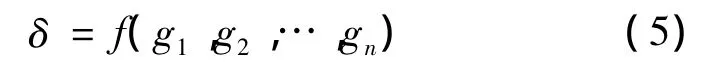
根据流体力学理论,喷氨射流经与烟气混合后,其浓度偏差δ与喷氨格栅几何参数之间的函数关系(5)应当为非线性函数关系。在给定喷氨格栅几何参数的情况下,求解氨气浓度分布属于正问题。尽管问题本身为复杂的非线性问题,但通过数值方法(Fluent软件)比较容易求解。而在给定氨气浓度分布的情况下,确定喷氨格栅几何参数,即求解方程(5),则属于逆问题。一般来说,逆问题(特别是非线性逆问题)的方程建立和求解,要比正问题更为复杂和困难。为此,本文这里提出建立代理模型,并结合优化算法对该问题进行分析求解。
首先在方程(5)基础上可构建多种代理模型,如多项式代理模型:

式中:g1,g2,…,gn为描述喷氨格栅的 n个几何参数;a0,a1,a2,a3,… 为议程系数。
其次,先选用一定的试验设计方法来选取m个初始样本点(m组几何设计参数),并对基于该样本点建立的喷氨格栅参数化模型进行数值模拟计算,以获得不同几何设计参数条件下对应的浓度偏差数值,然后,由该样本生成上述浓度偏差与喷氨格栅几何参数的函数关系(即确定上述方程中系数a0,a1,a2,a3…)。并以此作为后续优化设计过程中的代理模型。
在低理模型基础上,建立优化模型:
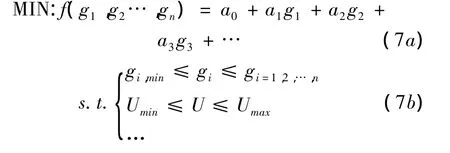
选用一种优化算法对该优化数学模型进行计算,以获得氨气最小浓度偏差时的喷氨格栅的几何设计参数。
1.3 喷氨格栅设计结果的性能评估与优化
对喷氨格栅进行参数化模型优化设计后,需要对设计结果进行计算和评估。由采用代理模型计算获得的最优(g1,g2,…,gn)建立数值计算模型,通过数值模拟分析,判断代理模型最优解f(g1,g2,…,gn与数值计算结果是否一致(即两者相差满足收敛要求),如果结果一致则优化完成,否则将此次数值计算结果添加到上述m个初始样本点中,即初始样本点增加为m+1个,重复步骤1)构造代理模型,继续优化,直至代理模型的优化结果与数值计算结果相一致。另外,还需对喷氨格栅和脱硝系统整体性能(如喷氨格栅导致的系统压降、喷氨截面与催化剂入口之间的预混空间等)进行评估,根据需求可适当修改初始设计方案重新进行优化设计。总之,要获得满足设计要求的SCR脱硝系统喷氨格栅,需要经过一个“设计—评估—修改设计—再评估”的反复设计迭代过程。
2 喷氨格栅优化设计应用实例与效果分析
本文拟为某SCR脱硝系统设计一个喷氨格栅。该脱硝系统内,喷氨格栅位置处烟道截面为10m×5m。烟气平均流速为5m/s,温度为600K。为有效脱除烟气中氮氧化物,所需氨气(体积分数5%)流量为4000m3/h。
根据对喷氨格栅设计要求的分析,制定初始设计方案:选定以喷氨管间距Ll、喷氨管上喷氨孔间距Ln以及喷氨孔直径D三个独立几何变量建立参数化模型;在均匀烟气流条件下,经混合长度Ld=2m,氨浓度偏差δ要求不大于2%;喷氨射流速度U要求不大于70m/s。
根据本文提出的基于参数化模型优化的喷氨格栅设计方法,首先构建如方程(6)所示的二次多项式响应面代理模型。
其次,本文选取了32个初始样本点,即D,Ll,Lh的32组不同取值,并经数值计算获得32组样本数据(δ,D,Ll,Lh)。由该样本数据生成代理模型:
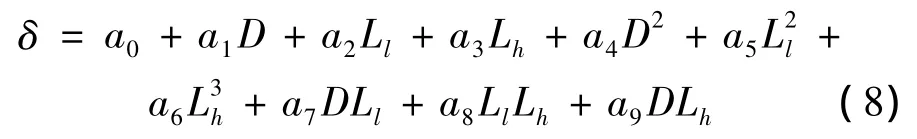
然后,在代理模型(8)的基础上建立优化计算数学模型:
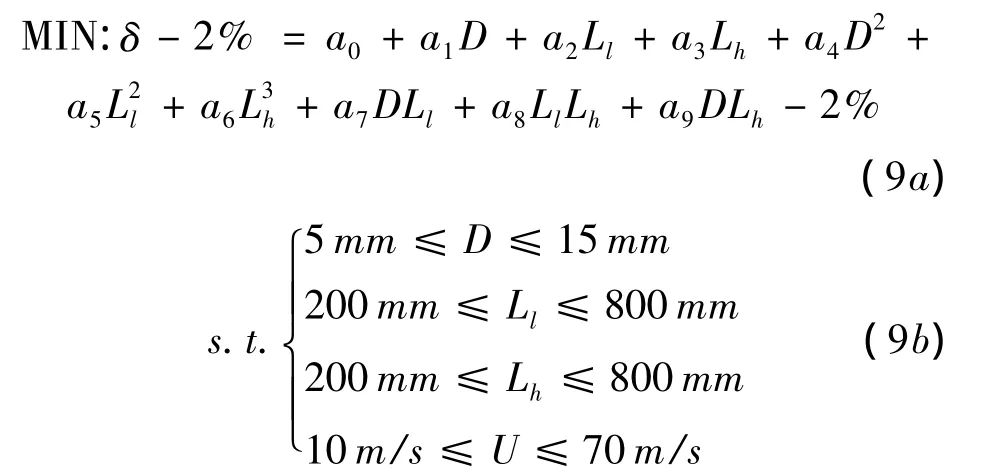
选用模拟退火算法对上述优化模型进行优化计算,结果表明当 D、Ll和Lh分别为6.0mm、365.5mm和326.5mm时,氨气浓度偏差为2%。
现将 D、Ll和 Lh分别取值为 6.0mm、365.0mm和326.0mm,建立喷氨格栅喷氨射流的数值计算模型,计算结果表明:经设计的混合长度后,氨气浓度偏差为1.4%,满足其不大于2%的设计要求。
3 结语
本文从喷氨格栅工程设计要求出发,结合数值模拟分析、代理模型技术以及优化设计方法,提出了一套基于参数化模型优化的喷氨格栅设计方法和流程,该方法对若干几何变量进行综合分析,最终可以实现喷氨格栅的最优设计。本文最后通过实例计算验证了该设计方法的适用性。该项研究可为喷氨格栅的工程设计提供一定的技术支持和参考。
[1]Pudasainee D,Lee S J,Lee S H,et al.Effect of selective catalytic reactor on oxidation and enhanced removal of mercury in coal-fired power plants[J].Fuel,2010,89(4):804 - 809.
[2]Yang Hongmin,Pan Weiping.Transformation of mercury speciation through the SCR system in power plants[J].Journal of Environmental Sciences,2007,19(2):181 -184.
[3]杨卫娟,周俊虎,刘建忠,等.选择催化还原SCR脱硝技术在电站锅炉的应用[J].热力发电,2005(9):10-14.
[4]Uddin M A,Shimizu K,Ishibe K,et al.Characteristics of the low temperature SCR of NOxwith NH3over TiO2[J].Journal of Molecular Catalysis A:Chemical,2009,309(1 -2):178 -183.
[5]Franco A,Diaz A R.The future challenges for clean coal technologies:Joining efficiency increase and pollutant emission control[J].Energy,2009,34(3):348 -354.
[6]Varner M,Rogers K,Hoover K.Channelized SCR inlet for improved ammonia injection and efficient NOxcontrol[P].US.6905658,2005.
[7]Albrecht M,Bock M,Rogers K,et al.Integrated air foil and ammonia injection grid for SCR systems[P].US.6887435,2005.
[8]Buzanowski M,Burlage P,Fadda D.Reagent injection grid[P].US.20060157132.
[9]Buzanowski M,Mark A,Fadda D.Optimized ammonia injection for power plant SCR systems[C].Proceedings of the ASME Power Conference 2007.San Antonio,United States:2007.
[10]Buzanowski M,Burlage P,Fadda D.Reagent injection grid[P].US.7383850.2008.
[11]Devarakonda M,Parker G,Johnson J H,et al.Model- based control system design in a urea-SCR aftertreatment system based on NH3sensor feedback[J].International Journal of Automotive Technology,2009,(10):653 -662.
[12]Chiang C J,Kuo C L,Huang C C.Model Predictive control of SCR aftertreatment system[C].Proceeding of the 2010 5th IEEE Conference on Industrial Elctronics and Applications.Taiwan,China:2009.
[13]蔡小峰.基于数值模拟的SCR法烟气脱硝技术优化设计[D].北京:华北电力大学,2006.
[14]陈海林.SCR烟气脱硝系统流场与浓度场的数值模拟及实验研究[D].镇江:江苏大学,2008.
[15]朱文斌.燃煤电厂SCR烟气脱硝装置的冷模实验和CFD数值计算研究[D].上海:上海交通大学,2008.
[16]雷达,金保升.燃煤电站SCR内烟气流场及还原剂浓度场模拟与优化[J].煤炭学报,2009,34(3):394 -399.
[17]孙琦明,徐 甸,施平平,等.CFD在火电厂SCR系统流场优化中的应用研究[J].技术与工程应用,2008,
[18]雷达,金保升.喷氨格栅处烟气速度场对高效SCR均流与还原剂混合性能的影响[J].热能动力工程,2009,24(1):113 -119.
[19]Simpson T W,Booker A J,Ghosh D,et al.Approximation methods in multidisciplinary analysis and optimization:A panel discussion[J].Structural and Multidisciplinary Optimization,2004,27(5):302 -313.
[20]穆雪峰,姚卫星,余雄庆.多学科设计优化中常用代理模型的研究[J].计算力学学报,2005,22(5):608 -612.
[21]Jin R,Chen W,Simpson T W.Comparative studies of metamodeling techniques under multiple modeling criteria[J].Journal of Structural Optimization,2001,23(1):1-13.
Parametric model-based optimization design method for ammonia injection grid
Combining numerical simulation,surrogate model and design optimization,ammonia injection grid design methods based on parametric model optimization of Selective Catalytic Reduction system were developed.First,parametric model is built according to the effect of geometric parameters of ammonia injection grid on ammonia diffusion.The design of ammonia injection grid is obtained by optimization.The feasibility of the design procedures is evaluated and verified by numerical simulation.
ammonia injection grid;parametric model;numerical simulation;surrogate model;design optimization
X701.7
B
1674-8069(2012)02-013-04
2011-10-29;
2012-03-16
李娜(1980-),女,辽宁抚顺人,博士,主要从事流体流动传热传质研究工作。E-mail:lina@gcleng.com

