基于光子晶体的高效太阳能电池反射器的研究

卢辉东，沈宏君*，吕冬妮，张 瑞

（宁夏大学 物理电气学院，宁夏 银川 750021）

基于光子晶体的高效太阳能电池反射器的研究

卢辉东，沈宏君*，吕冬妮，张 瑞

（宁夏大学 物理电气学院，宁夏 银川 750021）

设计了一种一维光子晶体的太阳能电池底部反射器，采用平面波展开法（PWM）计算禁带，得到当两个材料的介电常数差越大时，完全禁带越宽，对于Si/Air和Si/SiO2都在700～1 200 nm出现完全禁带，在此基础上利用勒让德多项式展开方法（LPEM）对该结构进行最优化，寻找到了高反射率时周期层数N，并考察了当入射角度不同时反射谱效率的问题，得出随着入射角度的增加，两种不同结构的一维光子晶体完全禁带均出现蓝移，证明了此种结构反射器具有高效的全方位反射性。把这种结构的背反射层用作太阳能电池的反射器可以大大提高电池的捕光能力，从而提高太阳能电池的的转化效率。

光子晶体；勒让德多项式展开法；反射器；太阳能电池

近些年，太阳能电池以其内在的优点得到了长足的发展，应用领域广泛。但目前太阳能电池光电转换效率大约在20%左右。因此，提高太阳能电池的转化效率是目前急需研究和解决的问题。研究者主要从这几点着手：减少光在太阳能电池表面的反射，即在电池的上表面加增透膜[1,2]；增加光路径，即设计高反射率的电池底部背反射层[3-6]；光陷阱[7]，延长光在电池体的停留时间。简单的说，太阳能电池的发电原理是利用太阳能电池吸收400～1 100 nm波长的太阳光，硅电池的弱光效应很好，其吸收光谱在300～700 nm，基本能吸收全部的可见光。但对近红外波长的光子吸收率很低，所以背反射层接受到的光线主要集中在长波长的近红外范围，在太阳能电池背部设置高效的反射器，可以使透过电池基体的长波光子充分反射，增加电池对长波长光子的吸收，从而提高光的利用率。目前应用广泛的是金属反射器和介质反射器[8,9]。然而金属反射器对光的吸收较大而无法获得高反射率。介质反射器能反射的波长范围窄及对光线入射方向较为敏感而难以实现全角度反射。本文设计了一维光子晶体结构做太阳能电池的反射器，对太阳能反射器的设计有指导意义。

1 理论模型

光子晶体[10,11]是折射率在空间周期性变化的介质结构，折射率的空间变化周期和光的波长为同一个数量级。和半导体一样，这种周期性材料的能谱具有能隙结构，称为光子禁带，频率落在此禁带的光子将被禁止在该光子晶体中传播。如图1所示是一种一维光子晶体用来做太阳能电池的反射器。

图1 背部结构的硅太阳能电池的示意图

2 数值模拟及分析

2.1 平面波展开法（PWM）和勒让德多项式展开法（LPEM）

计算光子晶体能带结构的理论方法有平面波展开法（PWM）、有限时域差分法（FDTD）、转移矩阵法（TMM）、多重散射法等，对于求简单的周期对称性的结构PWM有其内在的优势，它是基于对周期性介质，电场、磁场在倒格矢空间的展开，然后计算电磁场满足的本征方程，以求出本征频率，所以可以用来计算光子晶体的禁带结构。

勒让德多项式展开法[12,13]（LPEM）是基于麦克斯韦方程出发，把研究区划分为3部分，即入射波区（I区），中间的周期材料区（II区），最后光出射区（III区），I、III区的反射系数Ri和透射系数Ti由II区确定。

Ⅰ区（z＜0）：光波可以根据瑞利展式写为以下形式：

Ri、Ti分别为反射系数和透射系数，N是周期层数目，h是Si层的厚度，d是材料层的厚度。这里

在整个材料区中的电磁场的分布是满足麦克斯韦方程的，即：

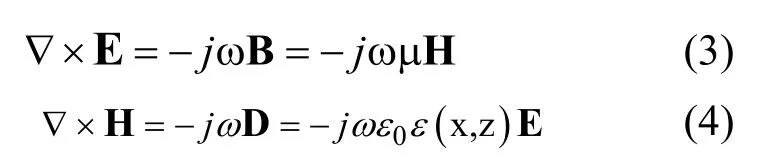
Ⅱ区（0＜z＜N( h+d )）：依据弗洛凯定理，TE偏振波的方程可写成如下形式：

把(5)、(6)代入(3)、(4)得线性微分方程，用伽辽金方法可以把微分方程转化成代数方程

将一维光子晶体分成L层，依据边界连续性条件，利用R矩阵：

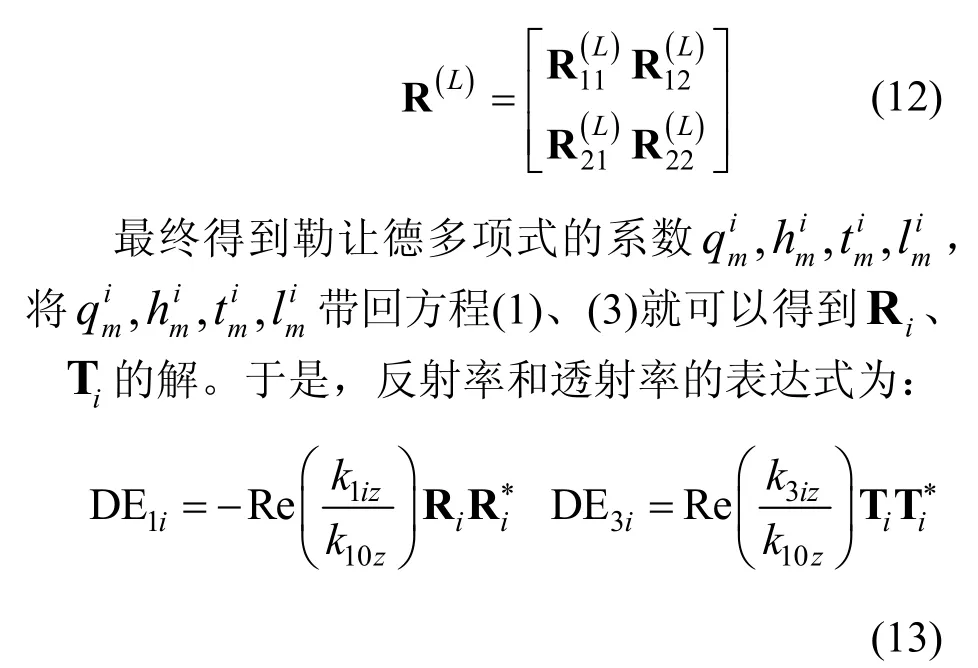
在整个光子晶体中，其能量是守恒的，总能量是1，即：

2.2 一维光子晶体的禁带结构

用平面波展开法计算一维光子晶体[14]的完全禁带，对于图1背反射层部分放大，具体研究图2的3种结构。

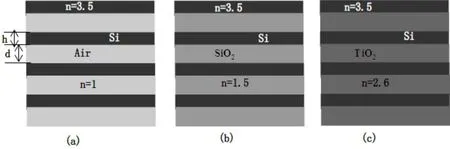
图2 一维光子晶体的多层膜结构

一维光子晶体由两种材料周期性交替排列构成，通常称为一维二元光子晶体，图2显示了3种由不同材料构成的一维光子晶体，Si层的厚度为h=λ/4nsi ，材料层的厚度为d=λ/4nx，其中nsi是硅的折射率，nx是材料的折射率，λ是一维光子晶体的中心波长，周期A=h+d,周期数为N。现在我们要研究太阳能电池对近红外光更好的吸收，这里中心波长取λ=900 nm，对于Si/Air一维光子晶体，h=64.3 nm、d=215 nm、A=279.3 nm；对于Si/SiO2，h=64.3 nm、d=150 nm、A=214.3 nm；对于Si/TiO2，h=64.3 nm、d=86.5 nm、A=150.8nm。用平面波展开法分别计算这三种结构的禁带为图3，对于Si/Air的归一化频率是0.201～0.442(wa/2πc)，对应的波长为627.6～ 1389.6 nm。Si/SiO2对应的归一化频率为0.179～0.306(wa/2cπ)，对应的波长为700.3～1197.2 nm。Si/TiO2对应的归一化频率为0.153～0.185（wa/2cπ），对应的波长为815.1～985.6 nm。可见，当两种材料的折射率差越大时，完全禁带越宽，完全禁带对应的波长将被禁止在光子晶体中传播，即100%的被反射会电池体。再加光子晶体对光子的吸收率为零，很好的克服了用金属作反射器的损耗问题。虽然Si/Air的完全禁带很宽，但是考虑到工艺制作方面空气层比较难把握，最好的应该是Si/SiO2周期层结构。由于Si/TiO2的禁带对应的波长在815.1～985.6之间，起不到很好的反射效果，故下面的分析中不在去研究它。

图3 三种不同材料的一维光子晶体禁带

2.3 周期层N对反射效率的影响

用LPEM研究一维光子晶体周期层结构的Si/Air及Si/SiO2，讨论了一维光子晶体周期层数N和组成材料折射率差对反射效率的影响。Si/Air结构[6]的一维光子晶体模拟结果如图4所示。取中心波长λ=900 nm，则Si和空气间隙的厚度分别为h=64.3 nm、d=215 nm，折射率分别为n1= 3.5，n2= 1，周期层厚度A=279.3 nm。由计算结果得，当N = 1、2时，反射效率低，当N=3、4时，波长在700～1200 nm的反射率可达99.99%，即N值越大，反射效率越到，N= 3已经可以满足高反射率的要求。

Si/SiO2结构的一维光子晶体模拟结果如图5所示。取中心波长λ=900 nm，则Si、SiO2的厚度分别为h=64.3 nm、d=150 nm，折射率分别为n1=3.5，n2=1.5，周期厚度A=214.3 nm。当N=1、2、3时，反射效率不高，当N=4、5时，反射效率的值接近稳定，波长在700～1 200 nm的反射效率是99.95%。故N = 4时就可以满足高反射率的要求。从上面可以看出，N值越大，反射率越高，且随着N值的增加，反射率的增幅变慢，当N达到一定值时，反射率将接近一个极限稳定值。构成一维光子晶体的两种材料的折射率差值越大，达到相同高反射率需要的N值越小。

图4 N=1～4时，Si/Air一维光子晶体反射率随波长的变化

图5 N=1～5时，Si/SiO2一维光子晶体反射率随波长的变化

2.4 入射角对反射效率的影响

因为太阳光中平均有15%是漫射光，会从各个角度射入太阳电池，故在太阳能电池的应用中，能否全方位反射是考察背反射器的又一指标。当入射角θ=0°、20°、30°、60°、89°变化时，考察一维光子晶体对反射率的影响。如图6、图7所示，随着入射角的增加，Si/Air和Si/SiO2均出现蓝移，且反射效率不断提高。对于Si/Air，完全禁带覆盖650～1 100 nm这一波长范围，对于Si/SiO2，完全禁带覆盖700～1 000 nm这一波长范围。故两种结构的光子晶体完全满足全角度反射的要求。如果再在背反射层的上表面制作成钝化结构，将会增大反射光的倾斜角度，使光在电池的横向方向传播，即延长了光的传播时间，起到慢光的效果来提高电池的捕光。

图6 不同入射角下，Si/Air一维光子晶体反射率随波长的变化

图7 不同入射角下，Si/SiO2一维光子晶体反射率随波长的变化

3 结论

本文设计了一种可用于太阳能反射器的一维光子晶体。结构是Si/Air和 Si/SiO2，应用PWM计算出禁带，算出禁带对应的波长范围，得出当两种材料的折射率差越大时，完全禁带越宽，达到相同反射率所需要的周期层数越少。再利用LPEM对这两种结构从可见至近红外波长范围内的反射谱进行了模拟计算，讨论了周期数N和入射角度变化时，对于Si/Air，N=3时，波长在700～1 200 nm，其反射率就可达99.9%，对于Si/SiO2， N=4时，波长在700～1 200 nm，其反射率可达99.9%。当入射角θ=0°、20°、30°、60°、89°，考察其对反射率的影响，随着入射角的增加，两种结构的一维光子晶体禁带均出现蓝移，且反射效率不断提高。完全光子禁带覆盖700～1200 nm这一波长范围。证明了此种结构反射器具有全方位反射的特性。故把这种结构的背反射层用作太阳能电池的背反射器可以大大提高电池的捕光能力。

[1] SAMEER C, MARTIN F S, et cl. Nanostructured multilayer graded-index antireflection coating for Si solar cells with broadband and omnidirectional characteristics [J]. Applied Physics Letters, 2008, 93(25): 251108-1-251108-3.

[2] MENNA P, FRANCIA G D. Porous silicon in solar cells: A review and a description of its application as an AR coating [J]. Solar Energy Materials and Solar Cells, 1995,37(1): 13-24.

[3] 李秀杰, 韩培德, 杨毅彪, 等. 基于光子晶体异质结的高效太阳能电池反射器研究[J]. 光子学报, 2010, 39(10): 1786-1789.

[4] ZHOU Dayu, BISWAS R. Photonic crystal enhanced light-trapping in thin film solar cells [J]. Journal of Applied Physics, 2008, 103(9): 3102-1-3102-5.

[5] BERMELP, LUO C, ZENG L, et al. Improving thin-film crystalline silicon solar cell efficiencies with photonic crystals [J]. Optics Express, 2007, 15(25): 16986-1700.

[6] 黎慧华, 王庆康. 硅薄膜太阳能电池背部反射结构设计[J]. 量子光学学报, 2009,15(4): 380-386.

[7] FAHR S, ULBRICH C, KIRCHARTZ T, et al. Rugate filter for light-trapping in solar cells [J]. Optics Express, 2008, 16(13): 9332-9343.

[8] FLORESCU M, LEE H, PUSCASU I, et al. Improving solar cell efficiency using photonic band-gap material [J]. Solar Energy Materials and Solar Cells, 2007, 91(17): 1599-1610.

[9] ZHAO L, ZUO YH, ZHOU C L, et al. A highly efficient lightrapping structure for thin-film silicon solar cells [J]. Solar Entergy, 2010, 84(1): 110-115.

[10] YABLONOVITCH E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics [J]. Phys. Rev. Lett, 1987, 58(20): 2059-2062.

[11] JOHN S. Strong localization of photons in certain disordered dielectric superlattices [J]. Phys. Rev. Lett, 1987, 58(23): 2486- 2489.

[12] KHAVASIA, MEHRANYK, RASHIDIAN B. Three dimensional diffraction analysis of gratings based on Legendre expansion electromagnetic fields [J]. Opt. Soc. Am. B, 2007, 24(10): 2676-2685.

[13] KHAVASIA, JAHROMIA K, MEHRANYK. Longitudinal Legendre polynomial expansion of electromagnetic fields for analysis of arbitrary shaped gratings [J]. Opt. Soc. Am. A, 2008, 25(7): 1564-1574.

[14] JOHN DJ, STEVEN G J. et al. Photonic crystal molding the flow of light [M]. Princeton University Press, 2008: 63-84.

Design of Highly Efficient Reflector of Solar Cells Based on Photonic Crystal

LU Hui-dong, SHEN Hong-jun*, LV Dong-ni, ZHANG Rui

(School of Physics and Electrical Information, Ningxia University, Yinchuan 750021, China)

A one-dimensional photonic crystal is designed for solar reflector, using plane wave expansion method (PWM) to calculate band gap, finding that the greater difference of the dielectric constant between two materials, the wider of the complete band gap. For Si/Air and Si/SiO2, there are totally 700～1200nm band, based on this, using the Legendre polynomial expansion method (LPEM) to optimize the structure, find a period at the high reflectivity of layers N, examines the issue of the incident angle reflection spectrum efficiency, that coming with the incident angle increases, the two different structures of one-dimensional photonic band gap crystals are completely a blue shift, proved that such a reflector has efficient all-round reflectivity. The structure of the back-reflection layer for solar reflector can greatly improve the light-harvesting capacity of the battery, Thereby enhancing the conversion efficiency of solar cells.

photonic crystal grating; Legendre polynomial expansion method; reflector; solar cell

O482.3

A

1008-2395(2012)03-0001-05

2011-12-23

国家自然科学基金项目（61167002）；宁夏自然科学基金项目（NZ1046）。

卢辉东（1987-）男，硕士研究生，研究方向：光子晶体。

沈宏君（1970-）男，副教授，博士，研究方向：光子晶体及其太阳能电池。