燃烧轻气炮发射药成分对内弹道性能的影响分析

邓 飞，刘 宁，张相炎

（南京理工大学 机械工程学院，南京210094）

燃烧轻气炮（Combustion Light Gas Gun，CLGG）是一种利用低分子量可燃气体燃烧后产生的高温、高压气体推动弹丸运动的新型发射系统.国外对燃烧轻气炮技术的研究已有十多年的历史，研究表明，这种发射技术所能提供的炮口动能比先进的固体发射药火炮高出至少30%，相应地，在火炮射程和发射弹丸质量上也有明显的优势.

燃烧轻气炮发射药采用轻质可燃气体，典型的装药成分有氢氧混合气体，甲烷、氧气混合气体等.研究表明[1]，预混气体的装填比例和少量惰性稀释气体对膛内燃烧稳定性和膛内温度有重要影响.刘宁[2]等首先建立了燃烧轻气炮准维内弹道模型，数值计算燃烧轻气炮内弹道过程，但未讨论发射药成分对内弹道性能的影响规律.为了研究发射药成分对燃烧轻气炮内弹道性能的影响规律，运用CFX软件建立了燃烧轻气炮的三维内弹道数值仿真模型，对不同装药条件下的燃烧轻气炮点火、燃烧过程进行了模拟分析，探索燃烧轻气炮最佳装填条件，为下一步实验研究提供依据.

1 物理模型

燃烧轻气炮原理结构如图1所示，轻质可燃发射药气体通过膛底输送管道注入燃烧室，轴线上的点火管可沿轴线多点点火.发射前，将弹丸输送至炮膛指定位置，弹后空间完全密封，然后向燃烧室内注入发射药预混气体，完成后关闭气体输送阀门，通过轴线上点火管点燃燃烧室内气体，燃烧后产生的高温高压气体膨胀，并推动弹丸沿身管向前运动.模拟中不考虑详细的点火机理，采用沿轴线五点点火的方法，且发射过程中无气体泄漏.

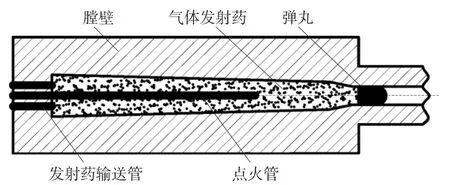
图1 燃烧轻气炮原理结构图

2 数学模型

2.1 控制方程

根据燃烧轻气炮装填条件和点火燃烧特点，提出如下假设：①发射药在点火前已经充分混合，点火后膛内气体进行预混燃烧；②膛内气体满足Peng－Robinson实际气体状态方程.膛内气体燃烧及流动的控制方程如下.

1）守恒方程. 燃烧室内气体燃烧流动过程为三维非定常可压缩粘性反应流动，各气体成分满足质量守恒方程、动量守恒方程、能量守恒方程以及组分输运方程，其统一形式可写为[3]

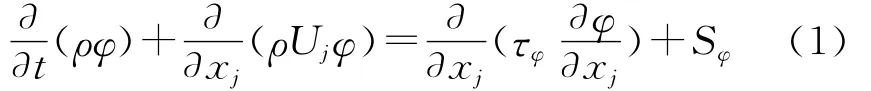
式中，各项分别为非定常项、对流项、扩散项和源项；变量φ分别对应于质量、动量、能量守恒方程中的变量；ρ为气体组分的密度；Uj分别为x、y、z方向的速度，下标j依次为坐标轴x、y、z方向；τφ为对应于变量φ的交换系数；Sφ为源项；dq为单位质量流体的热流量.

2）状态方程. 膛内气体采用实际气体Peng－Robinson状态方程，状态方程为

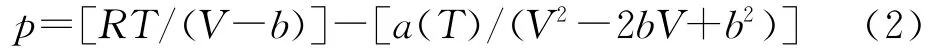
式中，V为混合气体比体积，系数a（T）、b由相应计算公式求出，混合气体的临界温度和压力由简化公式计算[4]，根据该状态方程和总装药能量计算出初始发射药装填压力.

3）弹丸运动方程. 弹丸运动过程所受的阻力用系数φp来描述，其运动方程为

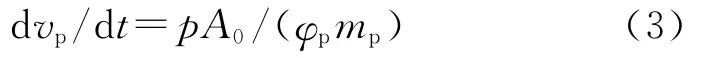
式中，取弹丸运动次要功系数φp＝1.4，vp、A0、mp分别为弹丸运动速度、弹丸底部面积和弹丸质量.

4）湍流及燃烧模型. 燃烧室内气体的湍流流动采用RNGk－ε双方程模型描述；气体燃烧过程采用EDM涡耗散模型，其基本思想是：当气流涡团因耗散而变小时，分子之间碰撞机会增多，反应才容易进行并迅速完成，故化学反应速率在很大程度上受湍流的影响，反应物的混合速率控制着燃烧速率[5].而反应物的混合速率取决于湍流脉动衰变速率ε/k，其原始控制方程为

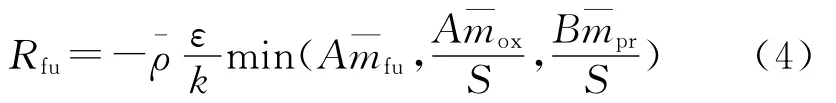
式中，A≈4，B≈0.5，S为化学恰当比，且该模型能用于预混燃烧和扩散燃烧，为未燃烧时混合气体密度与燃烧后气流密度之间的平均值分别为燃料、氧化剂、生成物浓度的时均值.

2.2 初边界条件

燃烧室初始条件：气体温度T＝T0，压力p＝p0，燃烧室容积V＝Vc.弹丸运动前，弹后空间完全密封，无气体泄漏.弹丸运动后，弹底为动边界，采用动网格技术进行处理.为了提高燃烧稳定性，采用轴线多点同步点火，且燃烧过程绝热.

3 模拟结果及讨论

3.1 模拟结果

以45mm燃烧轻气炮为算例，模拟中各参数采用文献[1]中某一实验的相应数据，其值见表1，表中T0为初始温度，p0为燃烧室初始装填压力，Vc为燃烧室容积，L为身管长，pmax为膛内最大压力，v′p为炮口初速.利用网格划分软件ICEM－CFD对模型进行网格划分，流体计算区域采用六面体网格单元，计算域网格总数为8.0×104，并且在燃烧室壁面设置3个压力记录点，即图2中的点P1，P2和P3，如图2所示.

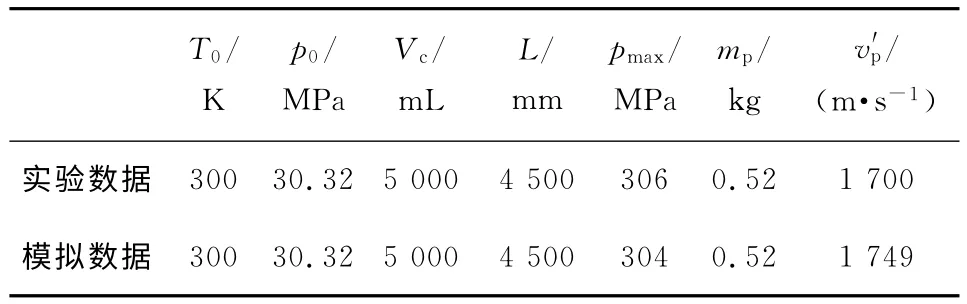
表1 45mm燃烧轻气炮实验与模拟结果对比

模拟结果显示炮口初速为1 749m/s，文献[1]中的实验结果炮口初速为1 700m/s，模拟结果与实验结果有着较好的一致性，说明本文建立的燃烧轻气炮三维数值仿真模型是合理的和可行的.

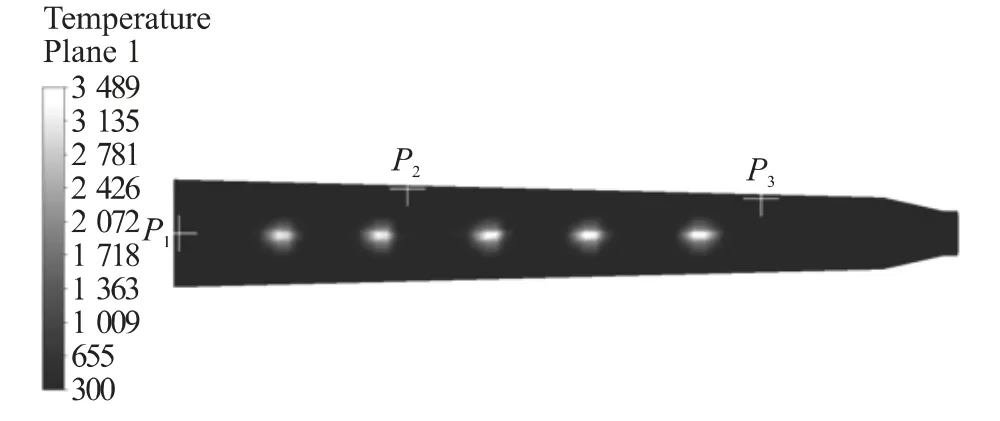
图2 燃烧室结构和点火时刻温度分布图（单位：K）

3.2 惰性稀释气体对内弹道性能的影响

为了分析不同含量的稀释气体对燃烧轻气炮内弹道性能的影响，选择3种不同的装填摩尔比：2H2＋O2＋nHe.其中n分别取2、4、6，即每组氢氧装填量不变，发射药总能量相同，只改变稀释气体装填量，弹丸质量为0.52kg.n取不同值时，在燃烧室P2记录点模拟得到的p－t压力曲线如图3所示.

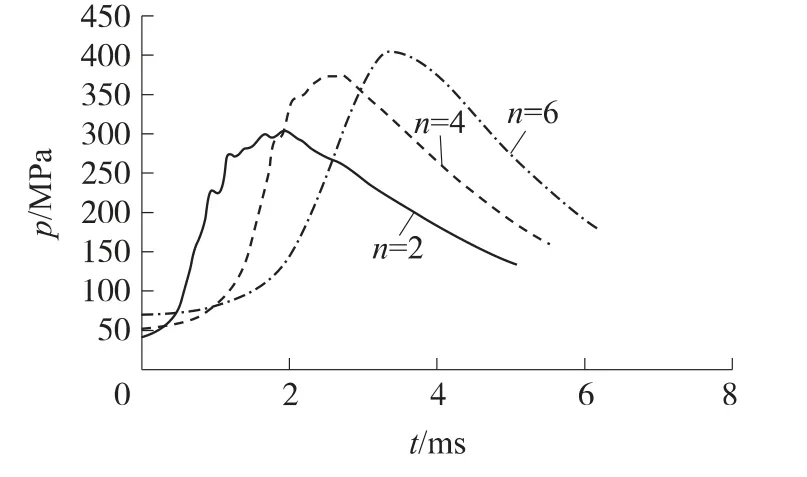
图3 不同稀释气体含量与P2点压力曲线图

由图3可知，在相同的发射药能量E＝6 MJ下，增加稀释气体含量，燃烧室内初始装填压力和最大压力将逐渐升高.同时，n值越大，压力上升加速度减小，压力波动逐渐减弱，这主要是因为增加稀释气体含量减缓了火焰传播燃烧的速度，提高了氢氧燃烧过程的稳定性.增加稀释气体含量可以起到提高膛内燃烧稳定性的作用，但是增加稀释气体含量使得初始装填压力升高，发射药装填难度增加.

图4为弹底压力pB与n值的关系，从图中可以看出，弹底的压力波动比燃烧室内更为明显，随着n值增大，压力上升加速度逐渐减小，压力波动减弱.

图5为稀释气体含量与燃烧室内平均温度变化关系.n＝2时燃烧室内最高平均温度接近3 450K，n＝4时平均温度最高值为2 650K，当稀释气体比例增加到n＝6时，室内最高平均温度降至2 000K.由于稀释气体对氢气燃烧释放热量的吸收耗散等作用，故增加其含量能够明显地降低燃烧室内的平均温度，有效减缓炮膛烧蚀现象.

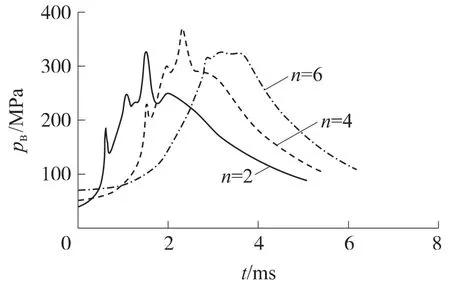
图4 不同稀释气体数量与弹底压力pB曲线图

图5 不同稀释气体含量与膛内平均温度T曲线关系

图6为弹丸速度与稀释气体含量的关系，从图中可知，随着稀释气体含量的增加，弹丸速度逐渐增大，这是由于稀释气体含量较小时，发射药气体初始压力低，膛内压力峰值较低，弹底压力小，弹丸加速度低，从而导致炮口初速较低.

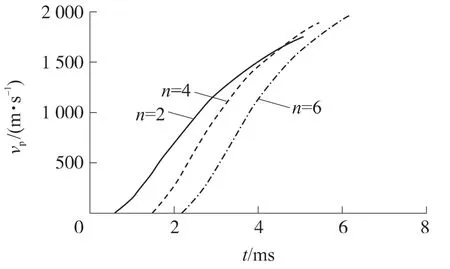
图6 不同稀释气体含量与弹丸速度vp曲线关系

3.3 发射药成分对内弹道参数的影响

采用不同的发射药成分，分析发射药的组成成分对内道弹性能的影响，采用3组不同装药成分，分别为氢、氧、氦混合，富燃料氢氧混合和甲烷、氧、氦混合.3种模型的化学反应方程式如下.

①氢氧氦：2H2＋O2＋4He＝2H2O＋4He.

②富燃料氢氧：6H2＋O2＝2H2O＋4H2.

③甲烷氦：CH4＋2O2＋4He＝CO2＋2H2O＋4He.

所有模型中发射药总能量为6MJ，弹丸质量为0.52kg.

图7为根据3组不同发射药装药成分计算得到的P2点处的压力曲线.从图中可以看出，第三组装填甲烷氦成分的初始压力值较低，其燃烧速度也较快，压力迅速上升，其最高压力在275 MPa左右；第二组富燃料氢氧装填时燃烧速度最慢，最大压力值比甲烷氦模型高，约为330MPa；第一组氢氧氦装填时膛内最大压力值最高，约为375MPa.在燃烧室压力波动方面，当装填成分为第一组氢氧氦和第二组富燃料氢氧时，压力波动现象不明显，压力变化较为平缓，而装填甲烷氦时压力波幅度最大，这主要与各燃料的热物性参数等特性有关.

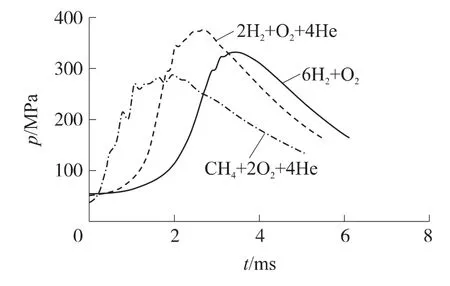
图7 不同发射药成分与P2点的压力曲线关系

图8为不同发射药成分对应的膛内平均温度曲线.在相同的发射药总能量条件下，甲烷燃烧的最高平均温度接近3 350K，燃烧速率也最快；氢氧氦燃烧时最高温度接近2 650K；富燃料氢氧燃烧的温度最低，最高温度值为2 250K，燃烧速率也最慢.说明了同等条件下三者比热容关系：氢气大于氦气，氦气大于甲烷.同时富燃料氢氧燃烧速度比相同条件下化学当量比氢氧燃烧速度慢.

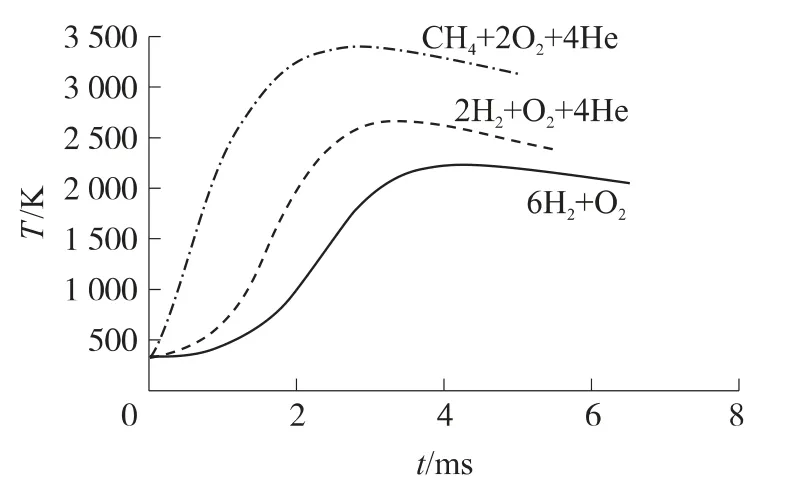
图8 不同发射药成分与膛内平均温度T曲线关系

图9为不同发射药成分时弹丸速度曲线，甲烷混合气体模型的弹丸速度最小，为1 698m/s，这是由于甲烷燃烧时弹丸启动时间较早，膛内压力较低，弹丸加速度小.氢氧氦燃烧模型燃烧室内压力较大，炮口速度最大，为1 900m/s.富燃料氢氧时其弹丸速度曲线和氢氧氦燃烧弹丸速度曲线形状较为相似，其炮口初速为1 814m/s.

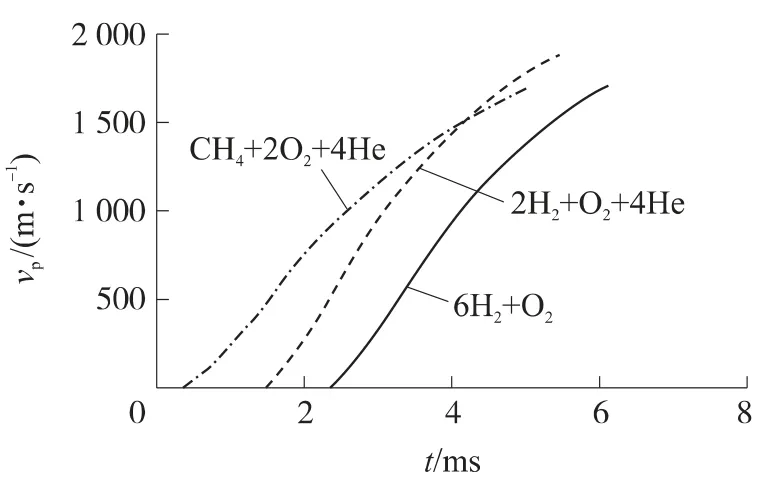
图9 不同发射药成分与弹丸速度vp曲线关系

4 结论

本文研究了燃烧轻气炮发射药成分对其内弹道性能的影响，基于CFD软件CFX对内弹道过程进行了数值模拟，计算结果表明：

①在相同发射药能量和装填组分的情况下，往发射药内加入较多的稀释气体（过量燃料、惰性气体）可以明显地抑制燃烧室内的压力波动现象，降低膛内平均温度，可以更好地控制发射药的燃烧，降低燃烧不稳定现象.同时，较高的稀释气体比例会提高发射药初始装填压力，对发射药加注设备和弹丸与身管间的密封性均要求较高，因此应根据实际条件采用适当的稀释气体比例.

②对氢氧氦、富燃料氢氧、甲烷氦3种不同发射药成分的燃烧过程进行数值模拟，发现在相同的化学能量条件下，甲烷氦的内弹道特性最差，这与甲烷的热物性有关，富燃料氢氧和氢氧氦模型具有较好的内弹道性能，膛内平均温度较低，压力曲线饱满，炮口初速较高.

[1]KRUCZYNSKI D，MASSEY D.Combustion light gas gun technology demonstration，ADA462130[R].2007.

[2]LIU Ning，ZHANG Xiang－yan.Quasi－dimensional interior ballistic model and numerical simulation of combustion light gas gun[C].Proceedings of the 26th International Symposium on Ballistics.Miami：IBC，2011：625－632.

[3]解茂昭.内燃机计算燃烧学[M].大连：大连理工大学出版社，2005.XIE Mao－zhao.Numerical combustion of engine[M].Dalian：Dalian University of Technology Press，2005.（in Chinese）

[4]童景山.流体热物性学－基本理论与计算[M].北京：中国石化出版社，2008：103－106.TONG Jing－shan.Fluid thermodynamics－base theory and compute[M].Beijing：Chinese Petrochemistry Press，2008：103－106.（in Chinese）

[5]赵坚行.燃烧的数值模拟[M].北京：科学出版社，2002.ZHAO Jian－xing.Numerical simulation of combustion[M].Beijing：Science Press，2002.（in Chinese）