某车载转管机枪刚柔耦合发射动力学分析

李洪强，廖振强，王 涛

（南京理工大学 机械工程学院，南京210094）

研究车载武器发射动力学主要有3种途径，分别是采用多刚体动力学理论、有限元法及多体动力学理论研究武器工作时的受力状态.多刚体动力学已经广泛运用于武器的设计研究，传统研究武器受力特性的方法都可以认为是多刚体动力学在武器研究中的具体运用，对于研究小口径，小威力的武器设计具有指导性的作用.然而多刚体动力学理论只能描述刚体运动而不能描述弹性运动，在高射速大口径转管武器系统中，武器发射威力的增大必然对武器发射平台产生巨大影响.膛内火药燃气对武器系统的后坐力将引起武器发射平台的变形，影响武器系统的作战性能，降低武器系统的射击精度.因此多刚体动力学的研究方法在处理该类问题时具有一定的局限性，不能准确反映大威力转管武器的发射动力学特性及零部件之间力及力矩的传递.有限元法在处理该类难题时存在建模难度大，计算工作量庞大的问题，限制了有限元法在处理较大武器系统动力学研究中的应用.本文考虑到射击过程中的武器变形对机枪射击密集度产生的影响，以多体动力学理论为依据，建立车载转管机枪的刚柔耦合模型，研究车载机枪武器系统的发射动力学特性[1].

1 模型的建立

转管武器指利用内部或外部能源驱动武器的枪管组和行星体转动，进而带动自动机与拨弹机构等相应零部件依次工作完成自动循环运动过程的武器系统.机枪发射过程中膛内火药气体压力作用于机枪上，通过缓冲簧将后坐力作用于摇架与托架上[2].后坐力一方面引起托架、摇架及其他零部件的变形，导致机枪在高低方向发生跳动；另一方面将破坏车辆在高低方向的稳定性，降低射击的密集度.

1.1 膛内火药气体压力及导气室压力的设置

发射过程中膛内火药气体压力是影响武器射击精度的主要因素：一方面，膛内火药气体压力的大小决定了作用于摇架上的后坐力的大小；另一方面，膛内火药气体作用的时间与频率决定了武器发射时的射击频率，即武器实际工作频率，工作频率与系统频率间的关系将影响武器射击过程中后坐力的变化和射击精度.

计算模型中机枪的稳定射击频率为3 000min－1，由经典内弹道方程得到内弹道时期膛内火药气体压力，根据经验公式得到后效期阶段膛内气体压力.导气室气体压力的计算方法有2种.其一是依据导气室的结构参数，利用经验公式计算得到近似的导气室压力变化曲线[3].但是，由于实际射击过程中枪管组及节套绕节套轴线的旋转速度存在波动，击发任意一发弹丸时，枪管组的转动速度均不相同.转速越快，导气室内气体容积变化越快，导气室压力变化越慢，因此射击过程中击发任意一发弹丸，导气室内的气体压力均不相同.根据经验公式得到的导气室压力曲线不能精确地反映持续射击过程中导气室气体压力实际的变化规律，从而导致自动机运动及整体振动结果的不准确.因此本文采用气体动力学的计算方法，建立导气室气体动力学微分方程组，计算导气室气体压力参数的变化规律，其计算式为

式中，pp，ρp，Tp分别为枪管膛内导气孔位置的气体压力、密度与温度；pq，ρq，Tq分别为导气室内气体压力、密度与温度；xh，vh分别为导气室内活塞的运动位移与速度；Sb，ΔSh分别为导气孔面积及活塞漏气面积；μb，μq分别为流入、流出导气室的流量系数；qm，b，qm，q分 别 为 流 入、流 出 导 气 室 的 气 体 流 量；Vq0，Sq0分别为导气室的初始容积与初始散热面积；ζ为临界压力比，ζ＝[2/（γ＋1）]γ/（γ－1）；Ff为活塞运动过程中受到的阻力，其他相关参数见参考文献[4].

1.2 零部件处理及零件之间的连接设置

由于计算模型的复杂性，计算模型中包括转管机枪自动机的动力学分析及整体车载武器系统的动力学分析，需要对系统模型进行适当的处理.托架、摇架及座圈支撑架是射击过程中后坐力的主要承受单元，枪管组件是分析武器射击精度的最重要单元，因此本文将枪管组件、托架、摇架、座圈支撑架等在射击过程中可能发生较大变形或主要影响射击精度的零部件进行柔性化处理，而将车辆本体、机匣及机枪内对射击精度分析影响较小的零部件以刚性零部件处理[5].

在模型中柔性体传递力及力矩的方式与刚体不同，需要在各柔性体上与其他关联零部件位置建立一刚性点与其他零部件传递力及力矩.各相互关联的柔性体之间的连接方式为：在两柔性体相互约束位置建立刚性连接点并与接触面上相关节点关联，接触面上各节点共同承担零部件之间作用力与力矩的传递.

机枪通过摇架导轨相对于摇架作纵向运动，并通过双向缓冲簧的弹簧阻尼系统描述机枪射击过程中的缓冲作用，双向缓冲器在往复运动过程中的运动微分方程为

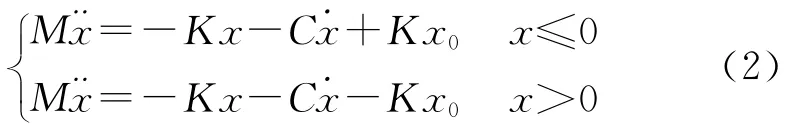
式中，K为缓冲簧刚度，取值为500N/mm；C为缓冲簧阻尼系数，取值为2.5N/mm2；Kx0为缓冲簧预压力，取值为500N[6].

车辆运动时将车辆后胎制动，认为车辆在射击过程中后胎只存在平动，前胎可存在平动与转动.采用弹簧阻尼系统描述车胎与地面之间接触关系，各轮胎与地面在垂直路面方向及沿车辆前后方向上的受力关系为

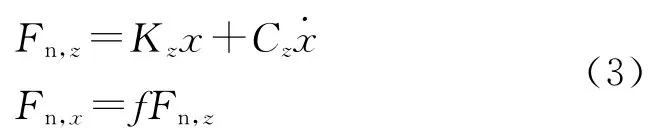
式中，Fn，z为在垂直路面方向上轮胎与地面接触力；Fn，x为沿车身前后方向上轮胎与地面的的摩擦力；Kz，Cz分别为在垂直路面方向上轮胎与地面接触刚度与阻尼；f为轮胎与地面之间的摩擦阻尼系数.

其物理模型如图1所示.

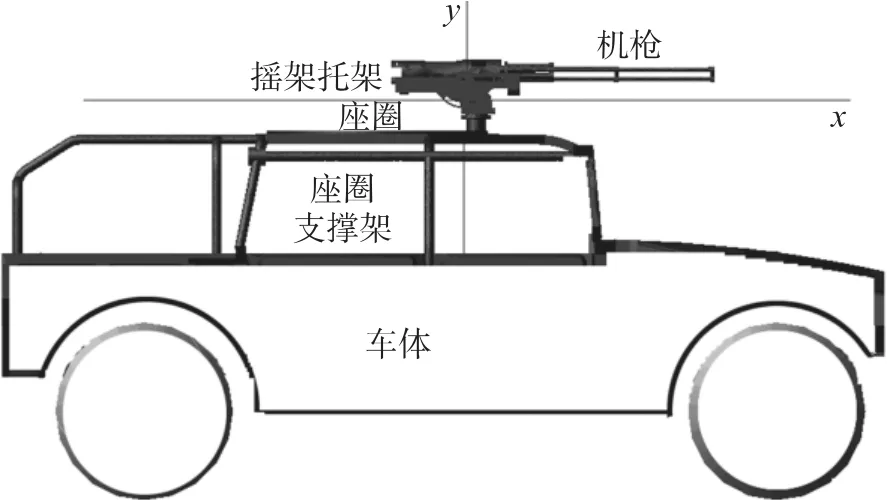
图1 车载转管武器模型

2 模型仿真分析

基于上述边界条件的处理及理论模型的分析，为了考察车载机枪射击过程中车辆响应对机枪射击过程的影响以及武器系统本身的机械特性，分析了转管机枪射击精度与后坐力的变化规律，对比分析了2组不同结构摇架、托架及座圈支撑架的机枪系统在车辆上射击时动力学特性优劣，并运用Adams软件仿真分析，采用求解精度高的SI2积分格式求解微分－代数方程组[5].原方案托架立轴长度大，立轴与座圈连接底座采用三角形空心支架，侧板及底板宽度小.根据零件有限元分析及试验结果，托架的结构刚度偏低导致机枪系统射击精度不够理想，因此本文对托架结构进行了优化处理.改进方案改变了托架结构布局，增加了托架侧板与底板的宽度，在两侧板之间增加链接筋板，减小了立轴的轴向长度，座圈与托架的连接座增加筋板，增强了连接座根部刚度，同时火线高度降低了106mm，改进前后方案的摇架托架结构见图2.

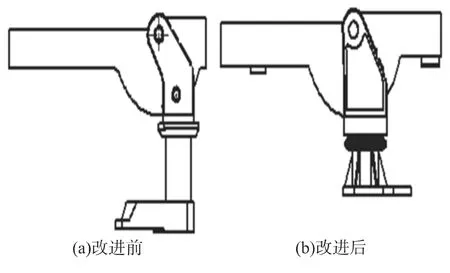
图2 改进前后摇架托架结构示意图

系统坐标系参见图1，沿枪管轴线向枪口方向为x轴正方向，沿纸面竖直向上方向为y轴正方向，z轴根据右手法则得到.为了描述射击时枪管在y方向（高低方向）的跳动情况，在枪管上沿枪管轴线方向取两标志点A和B，A点位于枪口，B点位于沿枪管轴线距枪口A点1 096mm处.根据射击时枪管上A、B两点在y方向与z方向的位移之差，就可了解枪管在高低方向的跳动情况.为了反映射击过程中机枪的射击精度，在计算过程中设置一传感器，记录弹丸出枪口时刻A、B两标志点在y方向的高度差.

2.1 原方案的发射动力学分析

根据前面建立的模型，得到表1所示原方案的发射特性计算结果，表中，F，D分别为后坐力峰值及后坐位移峰值；H为射击过程中枪口位置在系统坐标系中y轴的坐标；α1，α2分别为机枪与车体绕z轴振动角度；R70为机枪系统的70%的散布圆半径.具体变化规律见图3～图5，图中，α为高低方向跳动角.

表1 原方案计算结果

图3 原方案后坐力变化曲线

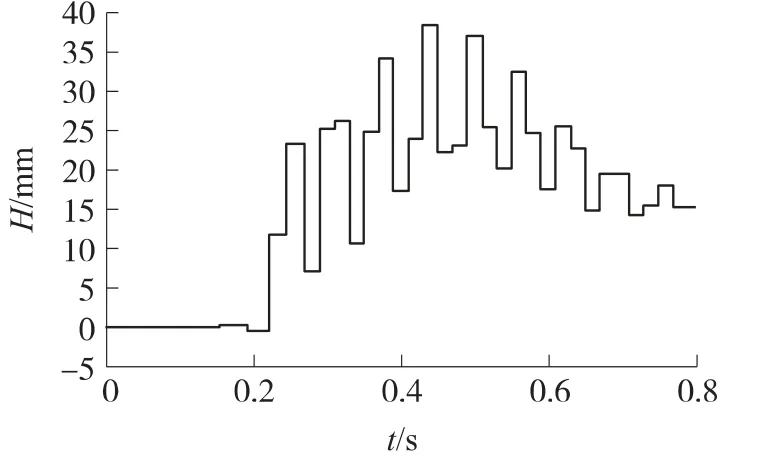
图4 在高低方向上原方案弹丸出枪口时刻枪口位移变化曲线

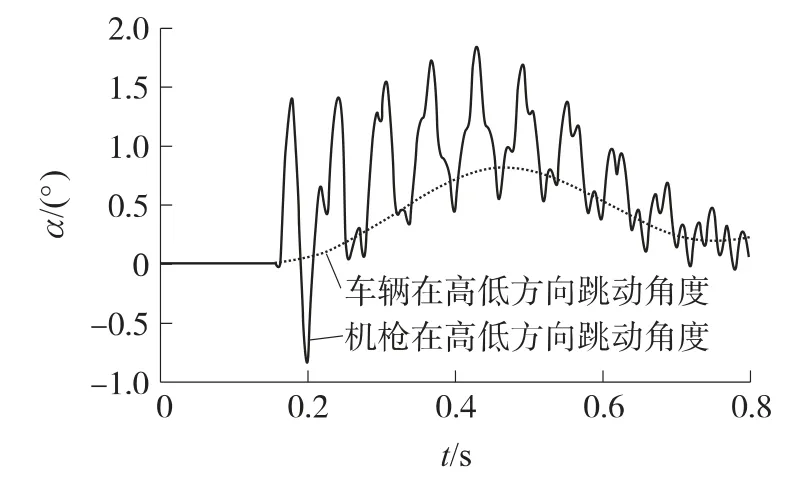
图5 在高低方向上原方案的机枪与车体的振动角度

图3为原方案机枪系统水平状态射击时后坐力的变化曲线，图中结果显示，由于武器系统射频大，在发射过程中缓冲簧基本处于后坐压缩状态，只是在初期未达到稳定射频时出现前冲后坐力，之后缓冲簧一直处于压缩状态.图4中阶梯竖线为计算模型中弹丸出枪口的时刻，横线为相应弹丸出枪口时.A，B两标志点在y方向的相对位移.计算结果表明枪口跳动基本上相对初始位置偏上，上跳位移大，每发弹丸出枪口时刻枪口位移值相差较大，取70%的有效射弹量，射击精度为15.6mil.图5为射击过程中机枪与车体在高低方向角位移的变化曲线.图中结果表明，机枪系统随车体在x－y平面内的振动而振动，且车体的振动较大程度地影响了机枪系统的射击精度，导致机枪系统射击密集度较差，车体高低方向最大跳动角度为机枪最大高低射角的44%，即枪管射角变化有44%是由于车体的稳定性不够引起的.原方案的分析结果显示，虽然武器系统的后坐力不高，但车辆在高低方向跳动稳定性仍然不够，导致车辆在后坐力的作用下在高低方向产生较大的角位移，进而影响射击过程的密集度，因此，必须从结构上改进武器系统，调整系统的相关参数.

2.2 改进方案的发射动力学分析

改进方案在结构上与原方案有较大改进，通过改变托架结构及其与座圈的连接方式降低了机枪射击时火线高度，改进了托架、摇架及支撑架结构.在基于上述模型设置的条件下得到表2所示结果，具体变化规律见图6～图8.

表2 改进方案计算结果

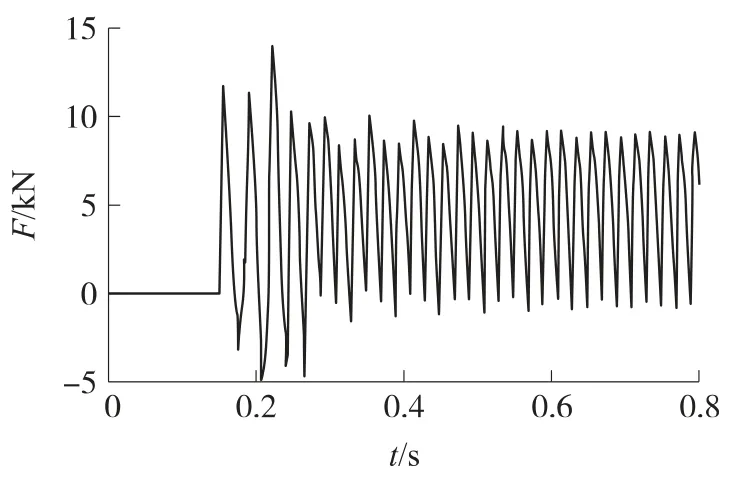
图6 改进方案后坐力变化曲线

图7 在高低方向上改进方案的弹丸出枪口时刻枪口位移变化曲线

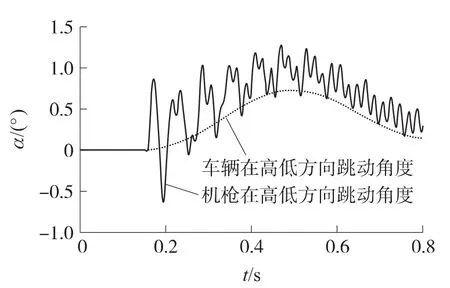
图8 在高低方向上改进方案的机枪与车体的振动角度

图6为改进方案的武器系统在水平状态下射击时后坐力的变化曲线，图中结果表明，2组方案在水平状态下射击时的后坐力基本相同，结构的改变没有引起后坐力的变化.图7与图4中结果相比，机枪系统在高低方向的跳动得到很大程度的抑制，改进方案的密集度有了显著的提高，取70%的有效射弹量，射击精度为11mil.图8为改进方案的车体与机枪在高低方向角位移的变化曲线，图中结果表明，车辆系统的稳定性得到提高，此时车辆的高低方向最大跳动与枪管在高低方向最大跳动都得到一定程度的抑制.

3 结论

通过上述2组方案分析结果可以得出：①车载武器系统的动力学分析与实际情况贴合，计算结果能够较精确地反映实际的武器射击规律；②武器系统改进前后其后坐力基本相同，武器发射平台的改进对机枪射击影响不大；③通过降低火线高度，改进托架摇架结构布局及座圈支撑架的结构，增加了武器发射平台系统的刚度，使得改进方案的武器系统的动力学特性改进明显，武器系统的射击稳定性得到提高，这证明了改进方案在提高武器性能方面的设计是行之有效的；④车辆振动对武器射击精度的影响较大，弹丸出枪口时刻枪口状态无法保持一致，要进一步提高武器射击精度，必须消除或减小车辆振动对射击精度的影响.

[1]毛保全，于子平，邵毅.车载武器技术概论[M].北京：国防工业出版社，2009：129－139.MAO Bao－quan，YU Zi－ping，SHAO Yi.Introduction of vehicle weapons[M].Beijing：National Defense Industry Press，2009：129－139.（in Chinese）

[2]戴成勋，靳天佑，朵英贤.自动武器设计新编[M].北京：国防工业出版社，1990：120－220.DAI Cheng－xun，JIN Tian－you，DUO Ying－xian.New design of automatic weapons[M].Beijing：National Defense Industry Press，1990：120－220.（in Chinese）

[3]廖振强，王涛，余世海.武器气体动力学数值计算方法[M].北京：国防工业出版社，2005：191－234.LIAO Zhen－qiang，WANG Tao，YU Shi－hai.Weapon and gas dynamics numerical method[M].Beijing：National Defense Industry Press，2005：191－234.（in Chinese）

[4]张高明，王瑞林，张本军，等.基于ADAMS的某型高射机枪虚拟样机建模与仿真[J].军械工程学院学报，2008，（6）：54－56.ZHANG Gao－ming，WANG Rui－lin，ZHANG Ben－jun，et al.Virtual prototype modeling and simulation analysis of antiaircraft machine gun based on ADAMS[J].Journal of Ordance Engineering College，2008，（6）：54－56.（in Chinese）

[5]樊磊，王亚平，刘一鸣，等.超轻量化高射机枪刚柔耦合建模和仿真[J].弹道学报，2009，21（1）：67－70.FAN Lei，WANG Ya－ping，LIU Yi－ming，et al.Rigid－flex coupled modeling and simalotion of a super－light antiaicraft Machine gun[J].Journal of Ballistics，2009，21（1）：67－70.（in Chinese）

[6]齐晓林.航空自动武器[M].北京：国防工业出版社，2008：194－234.QI Xiao－lin.Airborne automatic weapon[M].Beijing：National Defense Industry Press，2008：191－234.（in Chinese）