微控制器密码芯片秩相关电磁分析

李雄伟，张 鹏，陈开颜，赵 强

军械工程学院计算机工程系，石家庄050003

电磁分析(electromagnetic analysis，EMA)［1］是一种新型密码设备旁路攻击 (side channel attacks)破解技术，它通过测量密码设备在进行密码运算时辐射的电/磁场信号，研究电磁信号与内部处理数据间的相关性，从而获取密钥信息. 常用的电磁信号旁路分析技术包括均值差分法(difference of means)［2］、相关分析法(correlation analysis)［3］和模板分析法(template analysis)［4］等. 其中，相关分析因兼顾设备特征刻画能力与设备知识要求，在现实中具有很强的实用性. 而在相关电磁分析中，普遍使用的相关度量工具是Pearson 相关系数，这是一种线性度量方法［5］. 当电磁信号与内部数据线性关系不佳时，Pearson 相关系数法效果将大打折扣.

本研究提出一种基于秩相关度量的电磁分析技术，在一些Pearson 相关分析方法失效的场合下仍具有很好的分析与攻击能力.

1 微控制器电磁辐射信号特性

1.1 电磁信号与数据的相关性

任何密码系统的实现，终需硬件载体. 当前，硬件载体基本上都是数字集成电路芯片. 采用CMOS 工艺的微控制器(如AT89C52 单片机)就是一种典型的密码实现方式，它在工作时不仅消耗功率，同时向外辐射电磁信号. 通常直接辐射和无意辐射［6］两种电磁辐射可能与芯片中的秘密数据相关. 其中，直接辐射是指由密码芯片内部的电流所直接导致的电磁辐射，是电磁旁路分析中最常见的电磁信号源.

在CMOS 器件中，理想状态下电流只存在于器件的逻辑状态发生变化的时候，而状态变化是由算法执行所致.因此算法与器件逻辑状态变化，并由此产生的电磁辐射泄漏之间应存在某种对应关系. 本研究主要关注数据变化与电磁辐射信号间的相关性.

对于微控制器芯片来说，内部数据与电磁辐射信号之间最常用的关系模型为汉明权重(Hamming weight)模型［3］，当微控制器中当前操作数为D 时，汉明重量模型将电磁辐射信号能量建模为

其中，wH(D)表示D 的汉明权重，即D 的二进制表示中含有1 的个数;a 是由电路系统决定的常量因子;b 为随机噪声.

对确定的电路系统，若能通过适当技术消除噪声影响，并令a = 1，则模型(1)可简化为

1.2 直接电磁辐射信号分析实验

为验证上述直接电磁辐射信号数据相关模型的有效性，我们设计了物理分析实验. 针对AT89C52微控制器芯片，选择分析其指令集中的MOV 指令.该指令形式为MOV A，#01H，即将#后的立即数写入寄存器A，立即数宽度为1 byte，通过修改立即数，改变操作数的汉明权重.

为考察电磁探头与待测试芯片之间距离(测距)对结果的影响，实验分为微距与中距两类. 这里测距主要指探头与芯片之间的垂直距离;所谓微距，是指电磁探头直接接触芯片表面时，探头与内部电路之间的垂直距离，即芯片封装层的厚度;中距是相对微距而言，指电磁探头与芯片表面之间的垂直距离，约为5 ～30 cm. 不同距离接收到电磁辐射信号的精度，取决于所选取的探头类型与精度，以及于环境噪声的影响.

1.2.1 微距实验 针对AT89C52 芯片，选择wH分别为0，1，…，8 的操作数，形成9 条操作数不同的MOV 指令. 每条指令重复运行100 次，采样电磁探头紧贴芯片表面，运行过程中通过电磁探头的微距测量记录电磁辐射，共得到900 条电磁轨迹. 相同指令对应轨迹取平均值以去除噪声影响，得到9 条均值电磁轨迹，如图1.

图1 均值电磁轨迹与局部放大图Fig.1 The average EM traces fo nine MOV instructions using operands with different Hamming Weight

由图1(a)可见，操作数对于电磁轨迹的影响主要集中于尖峰处，即轨迹尖峰携带的信息量最大. 由图1(b)可见，操作数的wH与电磁辐射强度成反比，即wH=0 的操作数对应电磁辐射最强，wH=8 的操作数对应电磁辐射强度最弱.

为深入分析wH与电磁辐射强度之间的统计关系，对每条电磁轨迹上的第281 个点对应的电磁辐射强度进行打点绘图，计算不同wH对应样本点的均值与标准差，得到固定时刻电磁样本分布如图2.可见，不同wH与对应电磁辐射强度均值之间近似呈负线性相关，且样本抖动不大，标准差较小.

图2 微距实验固定时刻对应样本点分布图Fig.2 Sampling distribution at fixed time with zero-distance EM measures

1.2.1 中距实验 采样电磁探头分别放置于距52微控制器芯片垂直距离50、40、30、20 和10 cm处，由于这些位置噪声很大，因此对每种距离，每条指令重复采样1 000 条，共获得9 000 条电磁轨迹. 仍以第281 个采样点时刻为例，其中10 cm 对应的样本点分布情况如图3. 可见，不同汉明权重操作数对应的电磁辐射强度仍呈较强的负相关，但线性关系不明显.

图3 中距实验固定时刻对应样本点分布图Fig.3 Sampling distribution at fixed time with middle-distance EM measures

图2 和图3 表明，对于AT89C52 微控制器芯片，在去除量化噪声的前提下，微距测量时数据汉明重量与电磁辐射强度之间呈负线性相关，汉明重量相关模型有效. 在中距测量时，数据汉明重量与电磁辐射强度之间仅呈单调递减关系，汉明重量相关模型仍起作用，但精度受到影响.

1.3 相关度量方法

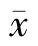
为应用Pearson 相关系数，要求总体具有二元正态分布，且测量至少具有间隔量表水平，对应分析实验可表示为不同汉明权重对应的电磁辐射强度呈线性关系，而中距测量时这种要求并不满足. 此时可采用更有效的Spearman 秩相关系数，这里，设N 个对象按X 和Y 变量进行评秩，评秩结果记为X1，X2，…，XN及Y1，Y2，…，YN. 当存在同分观察，即有两个或两个以上的对象就同一变量得到相同评分时，Spearman 相关系数rs［7］为

2 相关电磁分析方案

2.1 AES 密码算法

AES 算法［8］是一个使用可变分组和密钥长度，基于有限域运算的迭代分组密码. 以分组与密钥均为128 bit 的AES-128 为例，其算法主要包括初始轮密钥加(AddRoundKey)运算及后面的10 轮迭代. 本文将攻击中间点选择为AddRoundKey 运算.以加密为例，它是明文与轮密钥的异或操作，在微控制器中，其算法伪码为

其中，P 为明文;Key 为密钥;for 循环中的等式表达式相当于一个单条汇编指令，即1 byte 的明文与1 byte 的密钥进行异或，该循环将128 bit 密钥分成16 个子密钥块.

2.2 基于Pearson 相关分析的攻击

相关分析作为一种统计分析工具，已在功耗旁路攻击领域得到广泛应用. 本研究将其应用于电磁分析领域，构建进行密钥恢复的Pearson 相关性分析方案如下:

Step 1 选择被攻击设备执行密码运算的某个中间结果m，满足

其中，f ()是一个确定型函数或操作(如查找S 盒或异或);d 是已知非常量值，绝大部分攻击中d 既可以是明文也可以是密文，这意味着该类攻击属于已知明文攻击或已知密文攻击，以下均以已知明文为例;k 是未知子密钥，其所有可能的取值记为向量k= (k1，k2，…，kK)，其中K 表示可能取值的总数. k 中元素称为密钥猜测，显然其中必有一个元素等于设定的正确k，记为kck.

Step 3 对d 中任一元素di与k 中任一元素kj，利用式(6)计得猜测中间值f(di，kj)，全部猜测中间值构成D × K 的矩阵V，其中

显然，V 的第ck 列包含的是由正确密钥猜测kck计算得到的正确的中间值，该列中间值在D 次加密过程中确实被密码设备所处理到.

Step 4 将猜测中间值矩阵V 映射到电磁辐射值矩阵H. 映射的依据是汉明重量模型. 利用该模型，将每一个猜测中间值vi，j，模拟获得一个猜测的电磁辐射值hi，j，此时有

Step 5 对猜测的电磁辐射值和实际电磁辐射轨迹进行相关比较. 利用Pearson 相关系数，对H的每一列与T 的每一列进行相关性度量. 换言之，敌手需要将每一个猜测子密钥对应的猜测电磁泄漏与实际电磁泄漏的每一个位置进行相关比较. 其结果是K × T 的相关矩阵R. R 中各元素为

通过上述步骤，可获得正确的子密钥.

Step 6 更换其他子密钥，选择适当的攻击中间值，按上述步骤获取所有子密钥块，并最终得到完整密钥或最大限度降低完整密钥的搜索空间.

2.3 基于Spearman 秩相关分析的攻击

根据相关度量法分析，当采用中距测量时，Spearman 相关系数对相关性的度量更精确. 此时需根据式(4)，将Step 5 中R 中各元素计算为

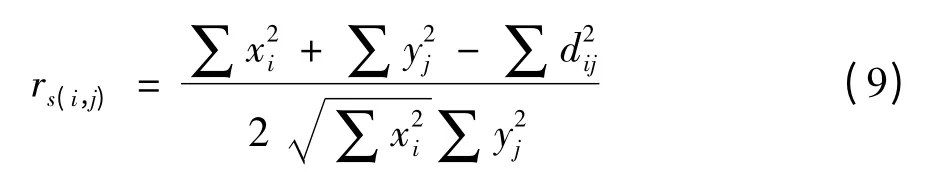
3 攻击实验

为比较上述攻击方案的效力，我们设计并实现了物理攻击平台［9］，对运行AES 的AT89C52 微控制器芯片进行微距与中距攻击.

3.1 实验配置

攻击平台包括数据采集与分析，其数据采集电路原理见图4. 图中数字表示平台的工作时序，可描述为:①对密码电路板供给输入电源与时钟信号，微控制器就绪并等待命令;②计算机对示波器进行配置与初始化;③计算机产生随机输入发送给微控制器，执行AES 加密;④微控制器给出触发信号，控制示波器开始采集;⑤示波器记录由磁场探头捕获并经放大器放大的电磁泄漏信息;⑥计算机接收密码运算输出;⑦计算机接收示波器发送的电磁辐射波形数据. 循环执行②至⑦，直到获取足够的攻击样本.

图4 相关性电磁分析实验电路原理图Fig.4 The circuit drawing of CEMA experiment

AES 使用的密钥预先存储在微控制器芯片中，计算机上用LabView 编写控制数字存储示波器的虚拟示波器，并由其控制数字示波器实时向PC 机传输电磁波形数据，实现了数据采集的完全自动化.数据分析由VC++与matlab 混合编程实现. 具体实验设备参数见表1，微距攻击实物图见图5.

表1 微控制器CEMA 攻击主要实验设备及参数Table 1 Parts of the devices and their parameters in CEMA against microcontroller

图5 微控制器微距CEMA 实物配置Fig.5 Zero-distance CEMA experimental setup against microcontroller

3.2 实验结果

所有实验均以获取AES 的前8 bit 密钥(设置为0x2B)为例，其余位密钥的获取方法类似. 设示波器采样率为250 Mbit/s，采样时间为4 μs，每条电磁轨迹共采样1 000 个点，将获得相关矩阵R256×1000中每一行取绝对值最大的点(即256 个密钥猜测分别对应的最大相关系数)作图，其中，中距测量结果如图6. 图6 中横坐标为密钥猜测，纵坐标为对应最大相关系数(R 中各行的最大值). 可见，正确密钥猜测(0x2B)对应的Spearman 相关性最大，由此获得AES 的前8 bit 密钥.

完整的对比实验结果如表2. 由表2 可见，微距测量时Pearson 相关性分析方法略占优势，中距测量时Spearman 相关性分析更为有效.

图6 微控制器中距CEMA 实验结果Fig.6 Experimental results of middle-distance CEMA against microcontroller

表2 针对AES 前8 位密钥的CEMA 攻击实验结果Table 2 Experimental results of time-domain CEMA against highest 8 bits key of AES

对未加防护的微控制器密码芯片来说，相关电磁分析可有效获取秘密密钥. 尽管相对线性相关度量方法来说，采用秩相关性度量会损失样本中的部分信息，例如，Spearman 秩相关检验的效率约为Pearson 相关系数的91%，即为揭示总体中的相关性，使用Pearson 相关系数法所需要的样本量是使用Spearman 相关系数法所需样本量的91%［6］. 但鉴于在相关电磁旁路分析实现时，所需样本量很大(一般大于1 000)，因此9%的功效损耗并不明显.相反，在线性相关度量失效的情况下，基于秩相关性度量的电磁分析技术仍能有效工作. 微控制器密码芯片的设计与制造者必须采取有效措施以抵御此类旁路攻击方法.

/References:

［1］ Quisquater J J，Samyde D. Electromagnetic analysis(EMA):measures and countermeasures for smart cards［C］// Isabelle Attali，Thomas Jensen. International Conference on Research in Smart Card，E-Smart. Canne(France):Springer，2001，2140:200-210.

［2］ Kocher P，Jaffe J，Jun B. Differential power analysis［C］// Wiener M. Advances in Cryptology，CRYPTO'99.Santa Barbara(USA):Springer-Verlag，1999，1666:388-397.

［3］Brier E，Clavier C，Olivier F. Correlation power analysis with a leakage model ［C］// Joye M，Quisquater J J. Proceedings of the 6th International Workshop on Cryptographic Hardware and Embedded Systems. Cambridge (USA):Springer，2004，3156:16-29.

［4］ Chari S，Rao J R，Rohatgi P. Template attacks ［C］//Kaliski B S. Proceedings of the 4th International Workshop on Cryptographic Hardware and Embedded Systems. Redwood Shores (USA):Springer-Verlag，2003，2523:13-28.

［5］ SHENG Zhou，XIE Shi-qian，PAN Cheng-yi. Probability and Statistics ［M］. Beijing:Higher Education Press，2001.(in Chinese)盛 骤，谢式千，潘承毅. 概率论与数理统计［M］. 北京:高等教育出版社，2001.

［6］Agrawal D，Archambeault B，Rao J R，Rohatgi P. The EM side-channel (s):attacks and assessment methodologies［C］// Kaliski B S. Proceedings of the 4th International Workshop on Cryptographic Hardware and Embedded Systems. Redwood Shores (USA):Springer-Verlag，2003，2523:29-45.

［7］Siegel S. Nonparametric Statistics for the Behavioral Sciences［M］. BEI Xing，translate. Beijing:Science Press，1986.(in Chinese)Siegel S. 非参数统计［M］. 北 星，译. 北京:科学出版社，1986.

［8］FIPS-197. Advanced Encryption Standard ［S］.

［9］ZHANG Peng，DENG Gao-ming，CHEN Kai-yan，et al. Electromagnetic correlation analysis attacks on microcontroller implementation of AES in far field ［J］. Journal of Huazhong University of Science and Technology:Nature Science Edition，2009，37(8):31-34.(in Chinese)张 鹏，邓高明，陈开颜，等. 针对AES 密码芯片的远场相关性电磁分析攻击［J］. 华中科技大学学报:自然科学版，2009，37(8):31-34.