大厂矿区地震与爆破记录波形特征分析

牟剑英，姚 宏，张 华

(广西壮族自治区地震局，广西 南宁 530022）

大厂矿区地震与爆破记录波形特征分析

牟剑英，姚 宏，张 华

(广西壮族自治区地震局，广西 南宁 530022）

运用小波理论和分形理论方法对大厂矿区典型爆破和显著地震事件波形进行定量处理和特征分析。先用小波理论对爆破和地震波形进行消噪处理，然后再运用分形维对爆破和地震波形进行定量处理和特征分析。结果表明：一般情况下取分维值为1.2可分辨该区的天然地震和爆破或其他干扰波动。

小波分析；分形理论；地震；爆破；识别方法

大厂矿区地震监测台网是全国首个金属矿区地震监测台网，台网由8个遥测子台和1个台网中心组成。台网孔径小，东西约7.5 km，南北约8.5 km，台站均匀分布，台间距平均仅3 km左右，监测震级下限低至ML-0.5级[1]。该台网自2009年下半年投入运行，记录到丰富的矿区地震事件，然而由于矿山开采爆破事件频繁发生，地震与爆破在同一区域交替出现，虽然地震和爆破具有不同的波形记录特征、时间和空间分布规律[2]，但准确地区分每个记录事件仍然存在一定的难度。

本文尝试将小波分析理论与分形理论相结合，应用于大厂矿区爆破或其它干扰源与天然地震波形的研究。首先利用小波变换对信号进行消噪处理，然后再运用盒数维对爆破与地震波形进行定量处理和特征分析，从而为开展矿山地震研究提供更为准确的基础资料。本文选取了自2010年以来大厂矿区地震监测台网记录的200余次ML≥0.7级事件，采用小波和分形方法对爆破和地震记录进行了对比研究，以探索定量辨识地震与爆破的方法指标。

1 基本理论简介

1.1 分形理论

分形 （Fractal）概念自1975年法国数学家曼德尔布罗特 （B.B.Mandelbrot）首次提出以来，已在许多领域获得了广泛的应用[3～5]。一些表面看来似乎杂乱无章，支离破碎的自然或社会现象，如大气中的湍流、雷电、云的形状，地表上的河流、海岸线形状、地壳内的断裂、地震分布，金属断面，化学活性表面，以及人类的经济活动等，通过分形研究，初步揭示出了其内在结构的规律性。分形作为非线性科学的一个部分，它为处理非均匀性和复杂现象开辟了新的思路，提供了新的工具。

自然界存在很多不规则的形态和现象，在不同尺度下观测均具有自相似的特点，其中任何一部分的放大都与整体相同或部分相同，通常人们把这种不规则性但又具有尺度不变性和自相似性的形态现象称为分形。分形的特点可用分维值来描述，其定义为：N∝r-D，其中N为尺度大于r的物体个数，即累积频数；D定义为某一分形体的分维值，它反映分形体形态结构的复杂程度。自相似性、无标度区、分维是其基本概念。自相似性是指被研究物体的局部性质 （形态、结构、功能、信息等）与整体性质相似，或每一个标度级别上的性质都相似。无标度区是指自相似性存在的尺度范围，标度是指尺度或测量单位。如果无论标度如何变，所研究的性质均不发生变化，则称被研究物体具有无标度性。分维又称分形维或分数维，在一般情况下是一个分数，是描述分形的定量参数。分形是多种多样的，描述其特征的分维也有多种形式，如容量维、信息维、关联维以及广义分维等。若用数学语言表述，分形是豪斯道夫 （Hausdorff）定义的严格大于拓扑维数d的集合[6]。其原理是：设A为Rn的一个紧子集，用尺度为的n维盒子来覆盖A，记Nt(A)是覆盖A的最少盒子数。集合A的Box维数DB(A)定义为：

1.2 小波理论

小波分析是二十世纪末发展起来的一种新的时域-频域分析方法，现已广泛应用于数字信号处理各个领域.小波分析是以泛函分析、调和分析、时频分析、数值分析、逼近论、广义函数论等学科为数理基础，建立在Fourier分析基础上的一门学科。Fourier变换反映的是信号或函数的整体特征，在不少实际问题中，我们所关心的是信号在局部范围中的特征。1946年D.Gabor引进了窗口Fourier变换概念，用一个在有限区间 (称为窗口)外恒等于零的光滑函数 (这个有限区间的位置随一个参数而变)去乘所要研究的函数，然后对它作Fourier变换。但是，Gabor引进的这种Fourier变换的窗口位置虽然能随参数变化而任意移动，其窗口的大小和形状却与频率无关，而是固定不变的。小波分析继承和发展了Gabor变换的窗口Fourier变换的局部化思想，使它的窗口随频率增高而缩小，同时又克服了窗口大小不随频率变化缺乏离散正交基等缺点[7]。

设函数f(t)∈L2(R)，定义其小波变换为：由定义可见，连续小波ψa，b(t)的作用与Gabor变换中的函数g(t-τ)e-iwt相似，参数b与 τ都是起着平移的作用。它们本质不同的是参数a与w，w的变化不改变窗口的形状与大小，而a的变化不仅改变了连续小波的频谱结构，也改变了窗口的大小。

近年来用小波分析广泛应用于各个数字领域[8～15]，对于小波阈值去噪，学者们主要关注三个方面：阈值去噪函数的建立、阈值的确定及小波基的选择。在阈值去噪函数的建立方面，Donoho和Johnstone等人于1995年提出了硬阈值方法和软阈值方法，之后有Garrote阈值函数及Gao和Bruce提出的半软阈值方法以对上述硬阈值和软阈值两种去噪方法进行了改进[16]。

2 资料的选取及数据处理步骤

2.1 资料的选取

本文选取了大厂矿区地震监测台网自2010年以来的记录的200多次ML≥0.7级矿区震动事件进行分析。选取的原则是：

（1）选取不经任何噪声滤波处理事件波形，根据仪器频响，只将数据换算成速度型记录。

（2）选取的事件主要发生在台站附近，尽量减少介质传播路径的影响，突出震源信息。

（3）所研究的地震波类型包括Pg波、Sg波和全波列记录数据。

（4）为了实现爆破与地震记录可对比分析，在选取台站波形时选用同一台站同一分向进行处理分析 (选取岜芒坪台垂直向)。

2.2 数据处理步骤

（1）对收集到的波形数据进行格式转换，将SEED格式事件数据 （国际通用格式）另存为EVT格式。

（2）根据波形数据发生的时刻，运用EDSP-IAS软件截取数据，考虑到研究区发生的显著地震和典型爆破都发生在大厂矿区监测台网网内，初动清晰，震动持续时间较短，所以一般截取长度为30 s或60 s。

（3）将截取数据存为文本格式，然后在MATLAB程序中实现波形显示。

（4）运用Garrote阈值函数对波形数据进行滤波。

（5）用盒数维对滤波后的波形数据进行计算，得到其分维值D。

（6）依据分维值区分爆破和地震事件。

3 爆破与地震波形分形特征

3.1 爆破波形的分维

全部选用了在对截取后的爆破波形进行Garrote滤波后，计算其分维数发现该区爆破的分维值变化在1.2-1.4之间 （见表1）。图1至图4给出了典型实例。

图1 2010年5月1日岜芒坪台爆破波形Fig.1 Blasting waveforms recorded by BMP station on 2010.05.01

图2 2010年5月1日岜芒坪台爆破波形分维值Fig.2 Fractal dimension values of blasting waveforms recorded by BMP station on 2010.05.01

图3 2010年10月17日岜芒坪台爆破波形Fig.3 Blasting waveforms recorded by BMP station on 2010.10.17

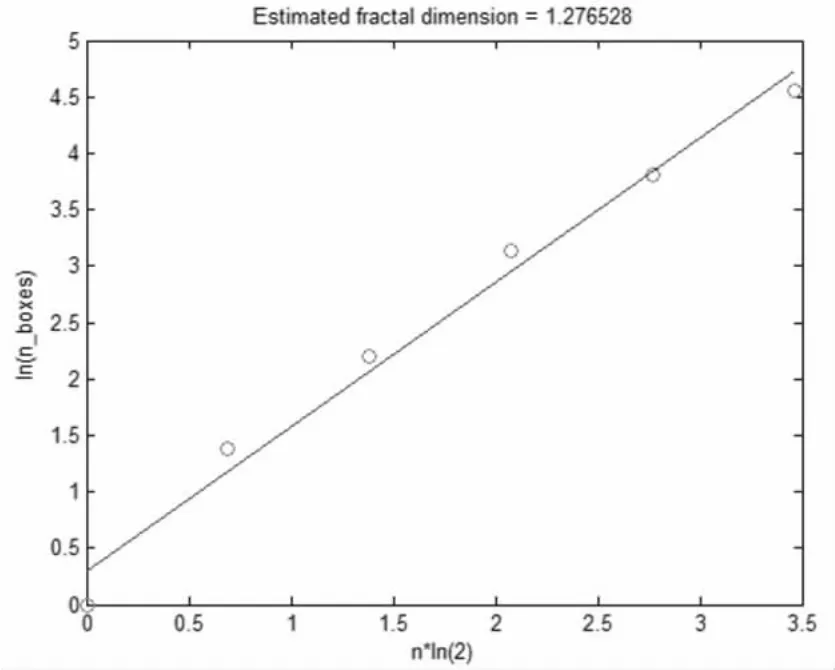
图4 2010年1月26日岜芒坪台爆破波形分维值Fig.4 Fractal dimension values of blasting waveforms recorded by BMP station on 2010.10.17

2010年10月17日，广西河池市南丹大厂矿区铜坑矿因采矿作业铜坑附近于16时6分20秒引爆近约48 t当量的炸药，监测震级为ML2.7级。事先已知道爆破的时间和地点，为监测和研究此爆破事件，特在附近 （约100 m处）架设了一套地震流动监测设备进行现场监测，并就其事件波形分维值进行计算，得出结果大于1.2。

3.2 天然地震波形的分维

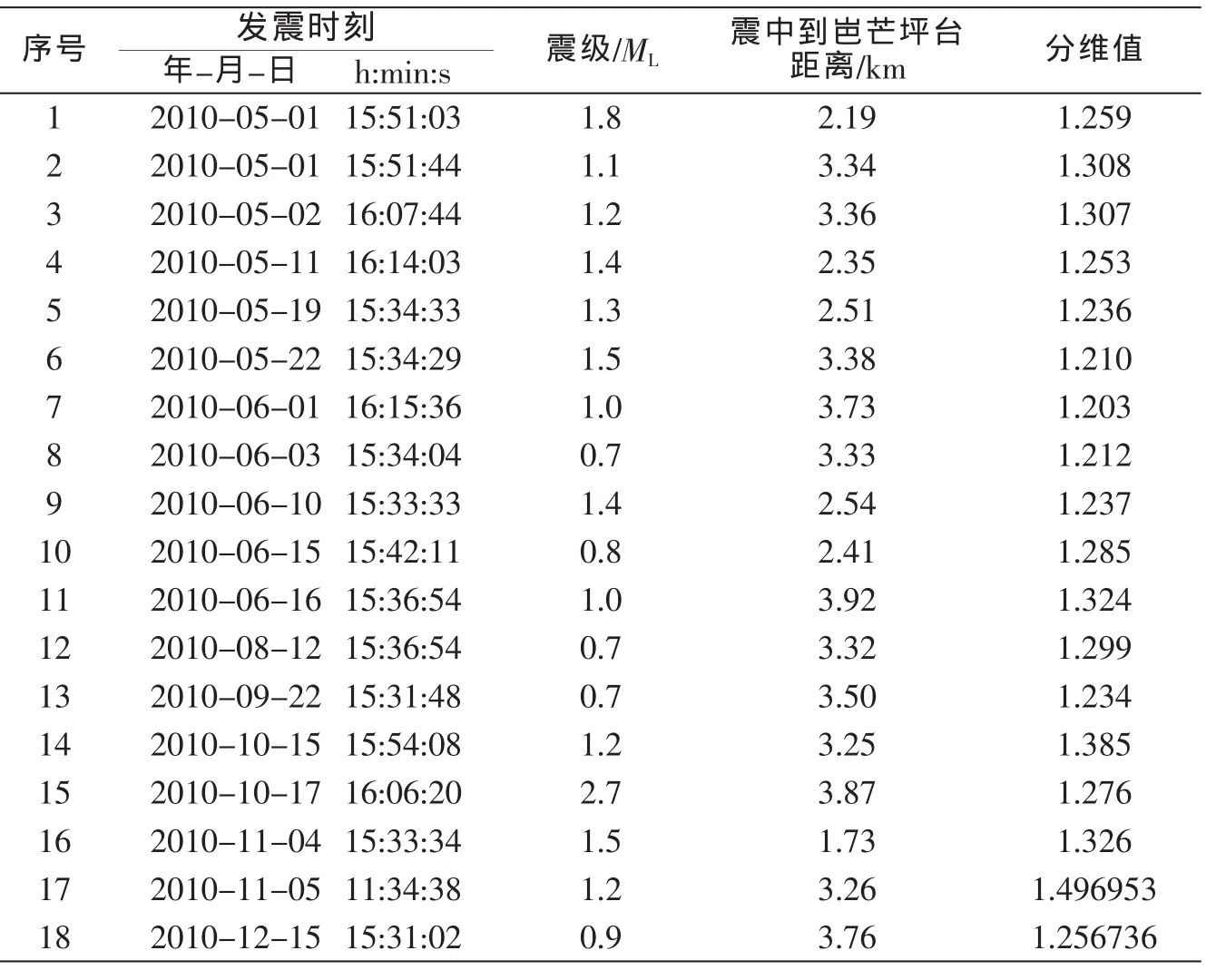
表1 大厂矿区典型爆破的分维值Table 1 Fractal dimension values of typical blasts in Dachang mining area

在对截取后的天然地震波形进行Garrote滤波后，计算其分维数发现该区天然地震的分维值变化范围在1.1～1.2之间 （见表2）。图5～8给出了典型实例。

2010年4月20日06时34分5秒，广西河池市南丹大厂矿区山草沟附近发生ML2.7级地震，经现场调查，此次事件为天然地震，并造成当地居民房屋墙体开裂的破坏。

图5 2010年4月20日岜芒坪台地震波形Fig.5 Seismic waveforms recorded by BMP station on 2010.04.20

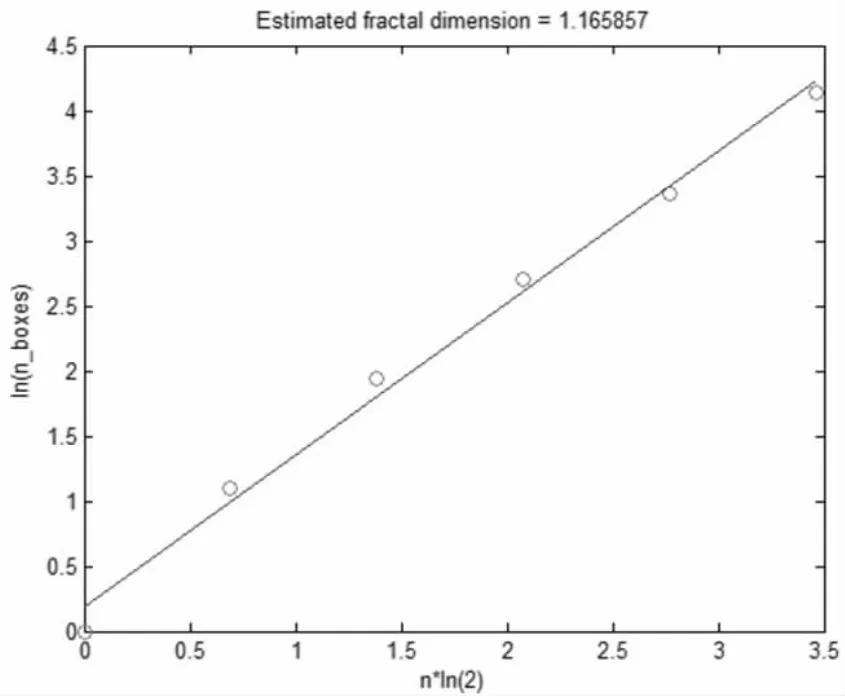
图6 2010年4月20日岜芒坪台地震波形分维值Fig.6 Fractal dimension values of seismic waveforms recorded by BMP station on 2010.04.20

图7 2010年8月11日岜芒坪台地震波形Fig.7 Seismic waveforms recorded by BMP station on 2010.08.11

图8 2010年8月11日岜芒坪台地震波形分维值Fig.8 Fractal dimension values of seismic waveforms recorded by BMP station on 2010.08.11

表2 大厂矿区地震的分维数Table 2 Fractal dimension of earthquakes in Dachang mining area

对天然地震和爆破信号进行Garrote滤波后，计算其分维数发现大厂矿区爆破的分维值在1.2～1.4之间，平均值为1.30；大厂矿区的天然地震分维值在1.1～1.2之间，平均值为1.17；在所记录的200余次ML≥0.7级的事件中，爆破事件都已向当地采矿部门核实了爆破时间、爆破地点和吨量，保证了数据的真实性和可靠性。因而可以设定1.2为区分大厂矿区爆破与地震记录的阀值。

4 结论和讨论

运用分形理论对大厂矿区地震监测台网矿震事件波形记录进行定量分析得出：区分大厂矿区天然地震与爆破时，应用分形盒维法是一种较为理想的方法。一般情况下取阈值1.2可以把大厂矿区中爆破与地震事件区分开来，或区分出其他如塌陷事件波形等非地震干扰源事件波形，这对矿山的安全生产和矿山地震研究都有极其重要的意义。同时因为震动事件的激发源不同、震源机制不同、波动所经传播路径的不同等因素都会引起的波形信号分维的变化。

虽然本文的研究结果能较好地适应大厂矿区的事件区分，但通过总结以往他人的研究结果，对于不同地区、不同震级大小事件和震中距范的不同，所获得的波形分维数有较大的差异。因此，若要定量区分某一地区爆破或地震记录，准确的做法还是根据本文提供的方法加以实际总结。

[1]杨松文，姚宏，陈鑫，等.广西大厂矿区地震台网技术系统设计[J].华南地震，2010，30（2）：97-106.

[2]姚宏，郭培兰，龙政强，等.广西南丹大厂矿区地震活动特征分析[J].地震，2010，31（3）：112-120.

[3]Allen R，Automatic earthquake recognition and timing from single trace[J].Bull Seism Soc Amer，1978，68: 1521-1532.

[4]Bear M，Kradolfer A，An automatic phase picker for local and teleseismic event[J].Bull Seism Soc Amer，1987，77：1437-1445.

[5]Dowding C H.Monitoring and control of blasting effects[J].Mining Engineering Handbook.Prentice Hall.1985：746-760.

[6]张晓威，江世媛.一类分形集的Hausdorff维数及相关结论[J].哈尔滨工程大学学报，1998，19(1)：94-98.

[7]刘志松.基于小波分析的信号去噪方法[J].浙江海洋学院学报，2011，30（2）：150-154.

[8]高勇军，陈小波.小波分析在爆破地震信号降噪中的应用[J].爆破，1999，16(3)：4-7.

[9]刘希强，沈萍，张玲，等.用小波变换能量线性度方法识别天然地震与爆破或塌方[J].西北地震学报，2002，25(3)：204-209.

[10]刘希强，杜贻合，徐波，等.区域矿震与地震的定量识别方法及其应用 [J].中国地震，2005，21(1)：50-59.

[11]孙甲宁，夏爱国，苏乃秦.地震和爆破时频域能量分布特征的对比分析 [J].华南地震，2005，25(2)：68-74.

[12]李金龙，董长利.数字地震记录的爆破识别[J].地震地磁观测与研究，2002，22(3)：28-35.

[13]何光明，高如曾.用小波分析提高地震资料的分辨率[J].石油地球物理勘探，1995，30（2）：257-263.

[14]刘泽民，小波分析在数字地震资料中的应用[J].地震地磁观测与研究，2004，25(1)：88-91.

[15]李信富，李小凡，武 晔.分形理论在地震学中的应用研究 [J].地球物理进展，2007，,22（3）：411-417.

[16]王宏强，尚春阳，高瑞鹏，等.基于小波系数变换的小波阈值去噪算法改进[J].振动与冲击，2011，30（10）：166-168.

Characteristic Analysis of Seismic and Blasting Waveforms Recorded in Dachang Mining Area

MOU Jianying，YAO Hong，ZHANG Hua

(Earthquake Administration of Guangxi Zhuang Autonomous Region,Nanning 530022,China)

This paper presents quantitative treatment and characteristic analysis on remarkable earthquake events and typical blasting waveforms in Dachang mining area using wavelet theory and fractal theory.Firstly we use wavelet theory to eliminate noise,then we use fractal dimension for quantitative treatment and characteristic analysis of seismic and blasting waveforms.The results show that fractal dimension value of 1.2 could be used to discern natural earthquakes, blasts or other intervention wave movements.

Wavelet Analysis；Fractal Theory；Earthquake；Blast；Recognition Method

P315.61

A

1001-8662（2012）03-0125-08

2011-11-17

广西地震局科研课题 （GXJ2011007）

牟剑英，女，1986年生，助理工程师.主要从事地震监测和数字地震学方面研究. E-mail：moussxf@163.com.