小波阈值算法的FPGA实现

王秀霞

（菏泽学院物理系，山东菏泽 274015）

小波阈值算法的FPGA实现

王秀霞

（菏泽学院物理系，山东菏泽 274015）

针对传统的阈值算法排序量多、消耗资源大和速度慢等缺点，提出了一种基于FPGA的快速中值选取器的设计方法.介绍了3点排序器和一种基于3×3点的中值选取器及其MATLAB仿真，针对基于3×3点的全流水并行243点中值选取器的结构利用率低，依据FPGA的硬件特点，设计了一种串并行交替的3n点中值选取器的硬件架构，阐述了快速中值选取器的硬件构架设计，对整个系统进行了仿真，并对仿真结果进行了分析说明.

中值选取器;现场可编程门陈列;阈值算法;串并行交替

阈值算法的硬件实现领域的研究仍然处于初级阶段，对于阈值算法具体应用方面（如小波滤波）硬件实现的研究多由商业公司进行，可供参考的资料较少.文献［2］提出中值的计算方法有多种，如果采用硬件计算的办法，不仅需要对噪声进行估计，还要进行开根号等运算，相对复杂且实现的意义不大.FPGA是基于查找表结构的可编程器件，具有丰富的寄存器资源，而且可通过系统内的重新配置来改变逻辑功能，如果将由软件或者先验知识得到的阈值由输入模块写入参数RAM中，需要的时候直接从RAM中读取，这样就使得设计的更新或修改十分方便.基于以上原因，本文提出了一种基于FPGA的串并行交替的3n点中值选取器的硬件设计.

1 阈值算法［1］

1.1 阈值的几种形式

1）由DONOHO提出的通用阈值方法，该方法认为小波变换能将信号的能量集中到少量的小波系数上，而白噪声在任何正交基上的变换仍然是白噪声，并且有着相同的幅度，相对而言，信号的小波系数值必然大于那些能量分散且幅值较小的噪声的小波系数值.因此，选择一个合适的阈值对小波系数进行阈值处理，就可以达到去噪声而保留有用信号的目的.

阈值公式如下

其中，N代表信号的长度，σ代表高斯噪声级数，即标准差，可以用下式估计得，即

其中，Det1代表最精细层的小波系数.

2）MinimaxShrink（最小极大方差阈值）和1）一样也是一种固定的阈值，使所选的阈值产生最小的极大方差.计算公式为

3）基于零均值正态分布的置信区间阈值

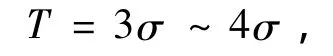
此阈值是考虑零均值正态分布变量落在［－3σ，3σ］之外的概率非常小，所以绝对值大于3σ的系数一般都被认为主要由信号系数构成.

1.2 阈值函数的几种形式 阈值函数的不同体现了对系数处理策略的不同，以及不同的估计方法.比较常用的2种阈值函数是:硬阈值函数和软阈值函数.

1）硬阈值函数的数学表达如下

其中，w（j，k）为含噪信号分解后的小波系数，λ为选定的阈值，wh（j，k）是硬阈值函数处理过的小波系数.硬阈值函数直接将绝对幅值不大于设定阈值的点设为零，而保留绝对幅值大于阈值的点.

2）软阈值函数的数学表达式如下

软阈值法不像硬阈值法那样只对幅值较小的小波系数实施抑制，而是对所有的小波系数进行抑制.

通过上述介绍可以知道，虽然阈值函数的解析表达式不尽相同，但是其之间却存在着以下共同点:

1）阈值的选择与高斯噪声级数，即标准差σ有关;

2）标准差σ由最精细层小波系数的中间值决定;

3）阈值函数的其他函数部分均可根据小波分解的层数，依据数学预算得到提前确定，即为一常数值.

依据以上共同点，可以得出结论:解决最精细层小波系数阈值选取的硬件实现是解决阈值算法硬件实现的最关键问题.

2 阈值算法硬件实现的MATLAB理论仿真

2.1 基于FPGA的阈值算法硬件实现面临的问题 在计算机应用中，中值算法已经相当成熟、高效，但对于FPGA来讲，还没有发现一种占用资源少、效率高的中值算法.为此笔者采取了诸多尝试，首先尝试着修改计算机中的冒泡法希望可以移植到FPGA中进行应用，但是发现假如将冒泡法应用在FPGA上会出现以下情况:

1）无法综合或者很难综合，极易产生错误;

2）严重耗费资源，延时不佳，若243点中值采用冒泡算法占用资源量是一般FPGA所吃不消的.

针对以上不足，笔者尝试过几种算法，例如，基于3点排序器的全流水结构的243点中值选取器，其基本思想是以3点排序器为设计的基本单元，首先用3点排序器组合成为3×3中值选取器，然后以3×3中值选取器为设计单元，采用并行全流水结构，构造出一个243点中值选取器.其结构示意图如图1和图2所示［3］.

图1 3×3中值选取器的内部构造

图2 基于3×3模块的全流水并行243点中值选取器

虽然基于3×3点的全流水并行243点中值选取器的硬件资源占用有所改善，但是耗费资源依然严重，需要耗费10 000多个以上LUTs，一般的FPGA仍然很难吃得消.

通过分析基于3×3点的全流水并行243点中值选取器的结构，发现了3×3中值选取器利用率很低，为此经过重新设计，并采用了一种新的设计结构:一种基于复用3×3中值选取器的串并行交替的243点中值选取器，其结构如图3所示.

图3 基于复用3×3中值选取器的串并行交替的243点中值选取器结构图

构建新结构的思想是将大量数据进行分段处理，做到少量多次，并用流水线结构使其达到实时处理的关键要求.

2.2 3点排序器及其MATLAB仿真 3点排序器模块的功能为:对3个输入数据进行排序，使其按照从大到小的顺序进行输出，其MATLAB仿真如图4所示.

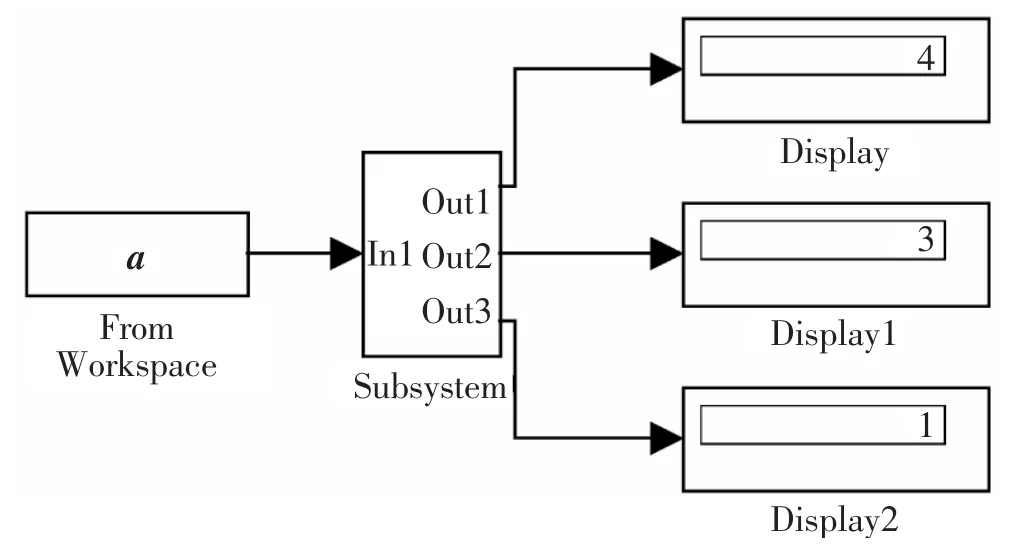
图4 3点排序器的MATLAB仿真

其中a为一个矩阵向量，在MATLAB中命令行中输入的是a=［3，1，4］;Subsystem的功能是实现对矩阵向量a的排序;Out1输出的为向量中的最大值;Out2输出的为向量中的中间值;Out3输出的为向量中的最小值.

2.3 9点中值选取器及其MATLAB仿真 9点中值选取器模块的构造是基于3点排序器的全流水结构，其模块功能为完成对3×3点数据的中值选取，其MATLAB仿真如图5所示.

其中，a，b，c分别为一个1×3的向量，在MATLAB命令行中输入的值分别为:a=［9，7，11］;b=［43，24，56］;c=［1，2，3］.Subsystem6的功能是完成对于3×3数据的中值选择.3个输出显示为3×3数据中值的可能值.需要指出的是:

1）依据MATLAB的仿真原理，巧用Workspace空间模拟出硬件流水线结构的工作流程.其中Subsystem，Subsystem1，Subsystem2为硬件流水结构的第1级流水处理模块，相应的Subsystem3，Subsystem4，Subsystem5为硬件流水结构的第2级流水处理模块;Fcn，Fcn1，Fcn2为硬件流水结构的第3级流水处理模块.

图5 9点中值选取器的MATLAB仿真

2）请注意各级输出数据的连接方式.例如，输出数据d由Subsystem的Out1，Subsystem1的Out1，Subsystem2的Out1组成.

即 d=［Subsystem.Out1，Subsystem1.Out1，Subsystem2.Out1］;d1=［Subsystem.Out2，Subsystem1.Out2，Subsystem2.Out2］; d2=［Subsystem.Out3，Subsystem1.Out3，Subsystem2.Out3］.

此后的d3，d4，d5的连接方式与以上的连接方式相同.

3 基于FPGA的阈值算法的硬件实现

3.1 Xilinx V5系列FPGA V5系列FPGA具有以下突出优点:1）采用最先进的最佳利用率高性能架构;2）强大的时钟管理模块（CMT）;3）采用先进的65 nm铜CMOS工艺技术;4）功耗低，内核电压仅为1.0 V;5）高级DSP48E块;6）内嵌高速RocketIO，速率高达3.2 Gbit·s－1.

本次设计采用Xilinx V5 XC5VLX50T FPGA，其具体参数，请参见文献［4］.

3.2 3点排序器的硬件FPGA实现及相关参数 3点排序器的外部接口如图6所示.

图6 3点排序模块

图7 3×3中值选取模块

3点排序器硬件模块，消耗130个LUTs，时钟最大延时为1.719 ns.

3.3 9点排序器的硬件FPGA实现及相关参数 9点排序器的外部接口如图7所示.

9点中值选取器硬件模块，消耗1 304个LUTs，519个slice registers;最高运行频率为156.286 MHz;时钟最大延时1.690 ns，工作使能信号最大延时1.712 ns.

3.4 243点中值选取器的硬件FPGA实现及相关参数243点中值选取模块的外部接口，如图8所示.

该硬件模块的外部模块设计简单，输入数据端口为x_in，位宽17 bit;输出数据端口为out_zhong，位宽17 bit;硬件模块工作时钟端口为clk，工作使能控制端口为re，输出使能端口为we.

图8 243点中值选取模块的外部接口

该硬件模块的工作过程为:数据以数据流的形式经过x_in端口持续输入，数据每243点为一组，进行种植筛选.时钟clk控制整个数据处理过程的节拍，工作使能信号re控制该硬件模块何时开始工作，何时停止工作.243点中值选取模块的输出为out_zhong.

243点中值选取器硬件模块，消耗6 015个LUTs，2 094个slice registers，最高运行频率为156.286 MHz，时钟最大延时1.690 ns，工作使能信号最大延时1.712 ns.

下面通过modelsim对243点中值选取器模块进行布局布线后仿真，观察243点中值选取器的设计是否满足实际要求，其仿真结果如图9所示.

图9 modelsim硬件仿真结果

例如输入数据1～486，则算出的中值为122和365，这与逻辑分析相同，设计正确无误.

基于全流水结构（729结构）和基于串并复用3×3中值器的实现的3n点中值选取器所消耗资源比较如图10所示.

从图10可以看出，基于串并交替的3n点中值选取器的硬件结构有如下优点:

1）耗费硬件资源少;2）中值选取器的点数越多，硬件设计就越能大幅度地节省硬件资源;3）确保有与全并行硬件结构相同的最高工作频率.

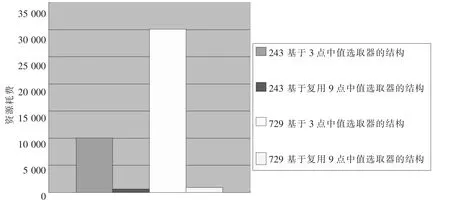
图10 2种不同硬件结构的资源消耗对比柱形图

4 结 论

依据现有中值滤波器的设计理念，利用3×3模板矩阵的特点，结合FPGA的并行特点［5］，采用3级流水及分时复用操作设计了一种串并交替的3n点中值选取器.与软件处理相比较，基于FPGA的快速阈值算法不仅能够提高处理速度，而且系统硬件结构简单、集成度高、消耗资源少、可靠性强、时序固定、延时小而且可以预见.

［1］DONOHO D I.De-noising by soft-thresholding［J］.IEEE Trans.Inform.Theory，1995，41（3）:613－627.

［2］许月圆.基于XILINX FPGA的小波滤波器设计与仿真［D］.西安:西安电子科技大学，2009:2－3，17－20，27.

［3］万海军，何东健，徐尚中.基于FPGA的图像中值滤波算法硬件实现［J］.微计算机信息，2008，24（21）:280－282.

［4］UG347.ML505/ML506/ML507 Evaluation Platform User Guide［EB/OL］.［2011－08－12］.http://www.xilinx.com/support/documentation/boards_and_kits/ug347.pdf.

［5］李轶博，李小兵，周娴.基于FPGA的快速中值滤波器设计与实现［J］.液晶与显示，2010，25（2）:292－295.

［6］李刚强，田斌，易克初.FPGA设计中关键问题的研究［J］.电子技术应用，2003，29（6）:68－71.

［7］胡越黎，计慧杰，吴频，等.图像的中值滤波算法及其FPGA实现［J］.计算机测量与控制，2008，16（11）:1672－1675.

［8］陈加成，徐熙平，吴琼.基于FPGA的中值滤波算法研究与硬件设计［J］.长春理工大学学报:自然科学版，2008，31 （1）:8－11.

Realization of Wavelet Threshold Algorithm Based on FPGA

WANG Xiu-xia

（Department of Physics，Heze University，Heze 274015，China）

There are some shortcomings of the traditional wavelet threshold algorithm，such as the more sort volumes，the more resource consumptions，and the more slow speed.In this paper，a design method of fast median selector based on FPGA was proposed.A three-point sorter，a 3×3 points median selector and their simulations in MATLAB were introduced.Focusing on the low utilization of 243 points median selector and based on the 3× 3 points and the features of FPGA，a hardware architecture of a points median selector was designed，which is serial and parallel.The hardware architecture of fast median select and the code realization of register transfer were introduced，the whole system was simulated，and the experiment results were analyzed.

median selector;FPGA;threshold algorithm;serial and parallel

TN 713

A

1004－1729（2012）01－0030－06

2011－10－12

山东省自然科学基金资助项目（Y2008A16）

王秀霞（1976－），女，山东定陶人，菏泽学院物理系讲师，硕士.