电位滴定—线性神经网络法用于工业碳酸钠的测定

叶芝锋

（广东南方碱业股份有限公司，广州广东 510760）

科学试验

电位滴定—线性神经网络法用于工业碳酸钠的测定

叶芝锋

（广东南方碱业股份有限公司，广州广东 510760）

尝试用电位滴定—线性人工神经网络法，测定工业碳酸钠生产过程中碳酸钠和碳酸氢钠含量及总碱量，并把测定的总碱量跟GB／T210.2－2004化学滴定法的结果进行比较，认为两种方法的测定结果吻合，而电位滴定—线性神经网络法不一定使用标准溶液，只要网络训练、测试和预测用的溶液浓度相同即可，滴定完毕后不用计算，只需用训练好的网络对测试集样本或未知样本进行仿真预测，即可得到测定结果。测试时既可以求得总碱量，也可以分别求得样品中碳酸钠和碳酸氢钠的含量，可以快速、准确、方便地用于生产过程控制分析。

工业碳酸钠；总碱量；测定；线性神经网络；MATLAB

众所周知，工业碳酸钠生产是通过测定总碱量来为过程控制提供依据［1］。缺点是：分析时间长，一个分析约需要40多分钟；耗用试剂多，一个分析需要1000mL蒸馏水，50mL盐酸标液；分析人员要全过程手工操作；同时提供的数据对生产控制还是显得有些粗糙。采用电位滴定法分析，一个分析只需要20分钟；蒸馏水和盐酸标液的消耗量也可以减半，不需要全过程手工操作，有助于实现分析自动化［2］。当今，人工神经网络由于能模拟人脑细胞（神经元）的工作原理，建立模型进行分类和预测，已经受到广泛关注，分析化学方面也有不少应用［3］。笔者尝试把电位滴定—线性神经网络法用于生产过程控制，结果表明，滴定不一定使用标准溶液，只要网络训练、测试和预测用的溶液浓度相同即可，滴定完毕后无需计算，只要用训练好的网络对测试集样品或未知样品进行仿真预测，即可得到测定结果。测试时既能提供总碱量的数据，也能给出样品的碳酸钠和碳酸氢钠的含量，可以快速、方便、准确地用于过程控制分析。

1 实验部分

1.1 方法原理

1.1.1 化学滴定法原理

见国标GB／T210.2－2004方法［1］。

1.1.2 电位滴定—线性人工神经网络法原理

测试时设定两个死停终点（pH＝8.4和pH＝5.1），滴定完毕后，在安装了MATLAB或类似软件的电脑上，将到达两个死停终点处盐酸标准溶液的耗用量，根据称取的试样量适当校正作为输入，用训练集样本的测试数据对线性神经网络进行训练，然后用训练好的网络对测试集样本或未知样品进行仿真预测，即可同时测定出样品中碳酸钠和碳酸氢钠的含量。测定样品总碱量时，根据滴定至pH＝5.1时盐酸标液的滴加量，校正后，输入到为测定总碱量训练的线型神经网络进行预测，就可得到测定结果［1］。

1.2 实验仪器与试剂

1.2.1 化学滴定法

酸式滴定管：50.00mL；锥形瓶：250.00mL。

1.2.2 电位滴定—线性神经网络法

仪器：雷磁JB－16电磁搅拌器；PHS－3C酸度计；酸式滴定管50.00mL；滴定杯。PC电脑1台（预先安装MATLAB或类似软件）。

试剂：盐酸标准溶液：1.001mol／L。

样品用量：2.5g左右（称准至0.0001g）；蒸馏水适量。

1.3 测定过程

配制的训练集、测试集和未知样分别用化学滴定法和电位滴定—线性神经网络法测定。

2 结果与讨论

2.1 训练集、测试集试样的配制

根据工业碳酸钠中碳酸钠和碳酸氢钠含量范围，用分析纯的试剂配制10个样品构成训练集，另配制5个样品构成测试集，见表1和表2。

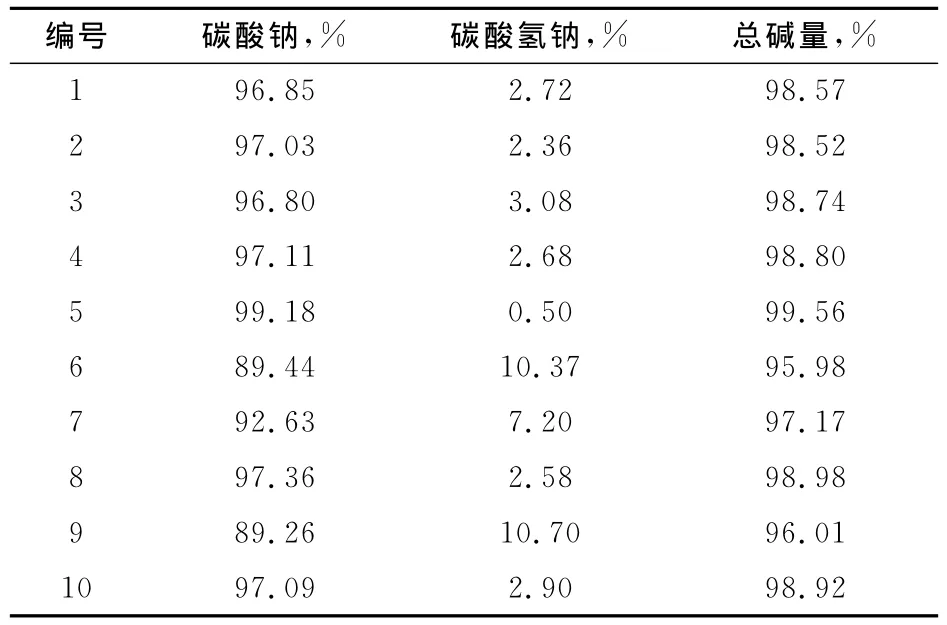
表1 配制的训练集试样浓度

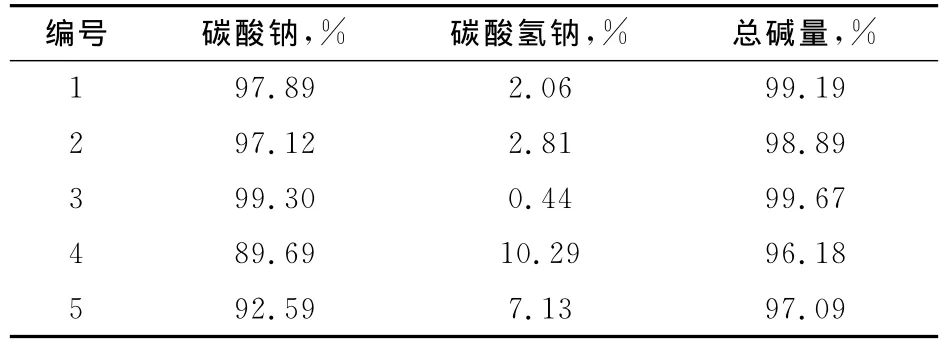
表2 配制的测试集试样浓度

2.2 电位滴定时滴定终点的选择

试验表明，采用国标GB／T210.2－2004化学滴定法测定总碱量时，指示剂变色时滴定溶液pH值约为5.1。而测定样品的碳酸钠和碳酸氢钠含量时，使用的双指示剂为酚酞和溴甲酚绿—甲基红，两者的变色点处的pH值分别为8.2～10.0和5.1左右，因此死停终点就分别确定为8.4和5.1［2］。表3和表4分别为训练集和测试集样品开始滴定到达pH＝8.4以及继续滴定到pH＝5.1时，滴加的盐酸标液的体积及试样的质量。

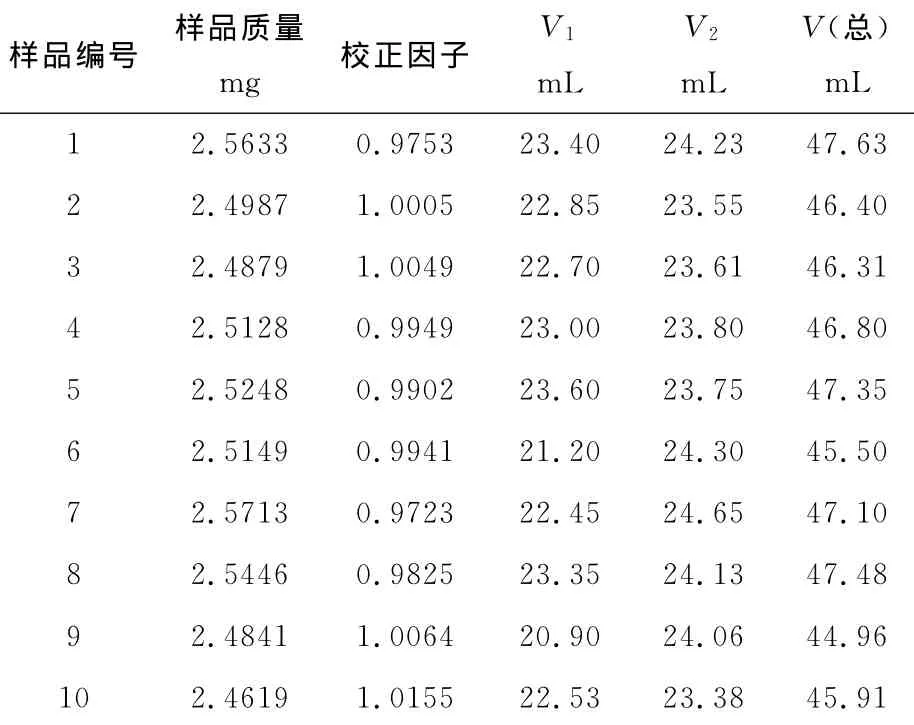
表3 训练集试样滴定时的体积数及试样的质量

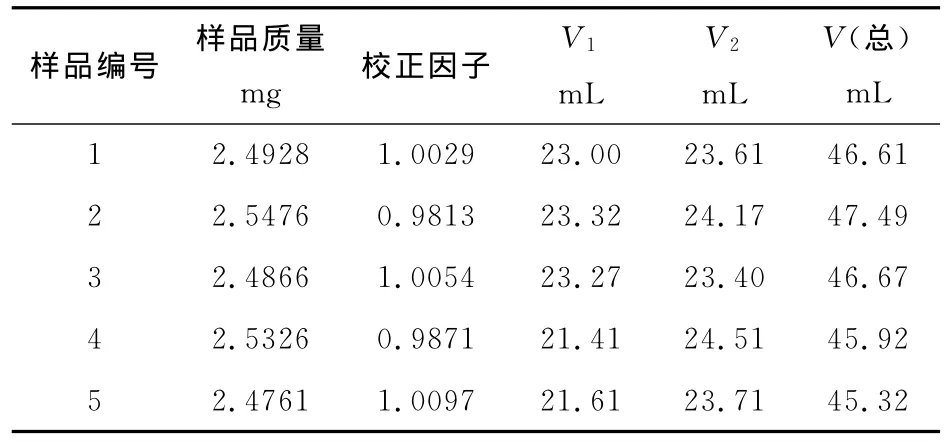
表4 测试集试样滴定时的体积数及试样的质量

2.3 线性人工神经网络算法

人工神经网络是模拟人脑神经网络的复杂网络系统，具有高维性、并行分布处理性、自适性、自组织性、自学习性等优良特性。人工神经网络模型的理论非常丰富，其输入层和输出层之间的信息转换计算方法也非常多，由于我们是使用MATLAB软件神经网络工具箱中的线性网络函数，解决碳酸钠分析的特定问题，因此对有关理论问题不作深入探讨，仅介绍如何使用工具箱中的有关函数解决该分析问题的情况。

已知用盐酸标液滴定碳酸钠试样中的碳酸钠和碳酸氢钠时，当溶液pH值到达8.4时，试样中全部Na2CO3被中和，全部变为NaHCO3，原有的NaHCO3仍然保持原来状态，即仍然为NaHCO3。继续用盐酸滴定到PH为5.1时，NaHCO3被全部变成了NaCl。上述两步化学反应都可以通过化学计量关系式计算［4］，因此这就为采用线型神经网络提供了依据［2］［5］。同理，样品总碱量的测定，也是根据滴定至pH＝5.1时的盐酸标液滴加量，用线性神经网络仿真预测。

线型神经网络是最简单的人工神经元网络，由一个或多个线性神经元组成，每个神经元的传递函数为线性函数，采用Widrow－Hoff学习规则或LMS（Least Mean Square）算法来调整网络的权重和阈值。

本文在测定样品中碳酸钠和碳酸氢钠含量时，采用newlind函数设计输入延迟的双输入、双层线性神经网络。调用格式为：

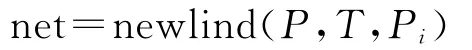
其中：P为训练集的网络输入，P1表示开始滴定到溶液pH到达8.4时，盐酸耗用的校正体积V1（mL），这是由于每个试样的取样量不会恰好为2.5 g，所以要将其校正之；同样，P2表示滴定时，pH从8.4至5.1时，滴定耗用盐酸溶液的校正体积V2（mL）。T1为训练集样品溶液中Na2CO3的含量，T2为其中NaHCO3的含量。Pi1、Pi2为延迟量。用训练集样品训练网络，然后用测试集样品，检验训练好的网络仿真的准确性，实际测试时，待测定样品滴定消耗的盐酸标液校正值，通过电脑用训练好的网络仿真，就可以求出Na2CO3和NaHCO3的含量［5］。

测定样品总碱量时，采用newlind函数设计单输入、单层线性神经网络。其调用格式为：

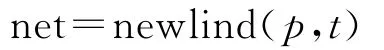
其中：p为训练集的网络输入，表示开始滴定到溶液pH到达5.1时，盐酸耗用的校正体积V（mL）。同理，由于每个试样称取量不会恰好为2.5 g，所以要将其校正之；t为训练集样品溶液的总碱量含量。用训练集样品训练网络，然后用测试集样品，检验训练好的网络仿真的准确性，实际测试时，待测定样品滴定消耗的盐酸标液校正值，通过电脑用训练好的网络仿真，就可以求出样品的总碱量含量［5］。

①测试样品中碳酸钠和碳酸氢钠含量使用的MATLAB神经网络函数程序：

a.训练线性神经网络并仿真：输入训练集P1延迟量Pi2＝｛5－1.45－1.2｝以及训练集P2延迟量Pi2＝｛5－1.45－1.2｝；输入开始滴定到pH＝8.4训练集校正后的滴定数据V1以及pH＝8.4到5.1训练集校正后的滴定数据V2；输入训练集碳酸钠浓度值T1和碳酸氢钠浓度值T2；训练线性神经网络并仿真。

b.测试集试样仿真：输入测试集试样校正后的滴定数据V1和V2；用训练集试样建立的线性网络对测试集试样仿真，考察建立的线性神经网络的预测准确性。如达到要求，就用来预测未知试样。

c.采用人机对话的方式，用建立的线性神经网络预测未知试样：根据电脑提示，输入未知样品的质量（g）、开始滴定到pH＝8.4滴定剂消耗量（mL）、pH＝8.4到pH＝5.1滴定剂消耗量（mL），回车，电脑就会显示未知样中碳酸钠和碳酸氢钠的含量。

②测定碳酸钠样品总碱量使用的MATLAB神经网络函数程序：

a.训练线性神经网络并仿真：输入训练集试样校正后的滴定数据p和对应的总碱量值t；建立和训练线性网络并仿真。

b.测试集试样仿真：输入测试集试样校正后的滴定数据P和对应的总碱量值T；用已建立的线性神经网络对测试集试样仿真，考察建立的网络预测准确性。如达到要求，就用来预测未知试样。

c.采用人机对话的方式，用建立的线性神经网络预测未知试样：根据电脑提示，输入未知样品的质量（g）、开始滴定到pH＝5.1滴定剂消耗量（mL），回车，电脑就会显示未知样的总碱量测定值。

2.4 测试精密度考察

表5为精密度考察数据。由表可见，测试的精密度达到了国标方法的要求。

2.5 两种方法测定成对测定值的比较

对子分析常用于比较一个新分析方法和另一方法所测定的一系列试样分析结果的差异程度［6］。其计算公式如下：

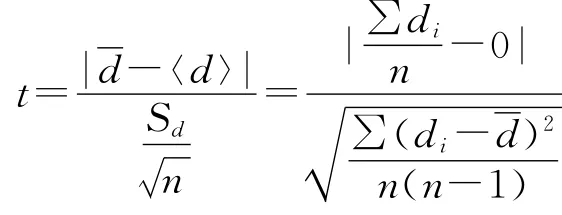
式中：di为同一试样两个测定结果之差；d为配对数据差值的平均值；

〈d〉为配对数据的期望值，等于0；Sd为配对数据差值的标准偏差。

表6是两种方法测定的“对子”数据表。可以看出：︱t︱＜t0.05，8＝2.306，所以有95%的把握，认为两者测量结果的平均值无显著差异。（t0.05，8＝2.306为查表所得）

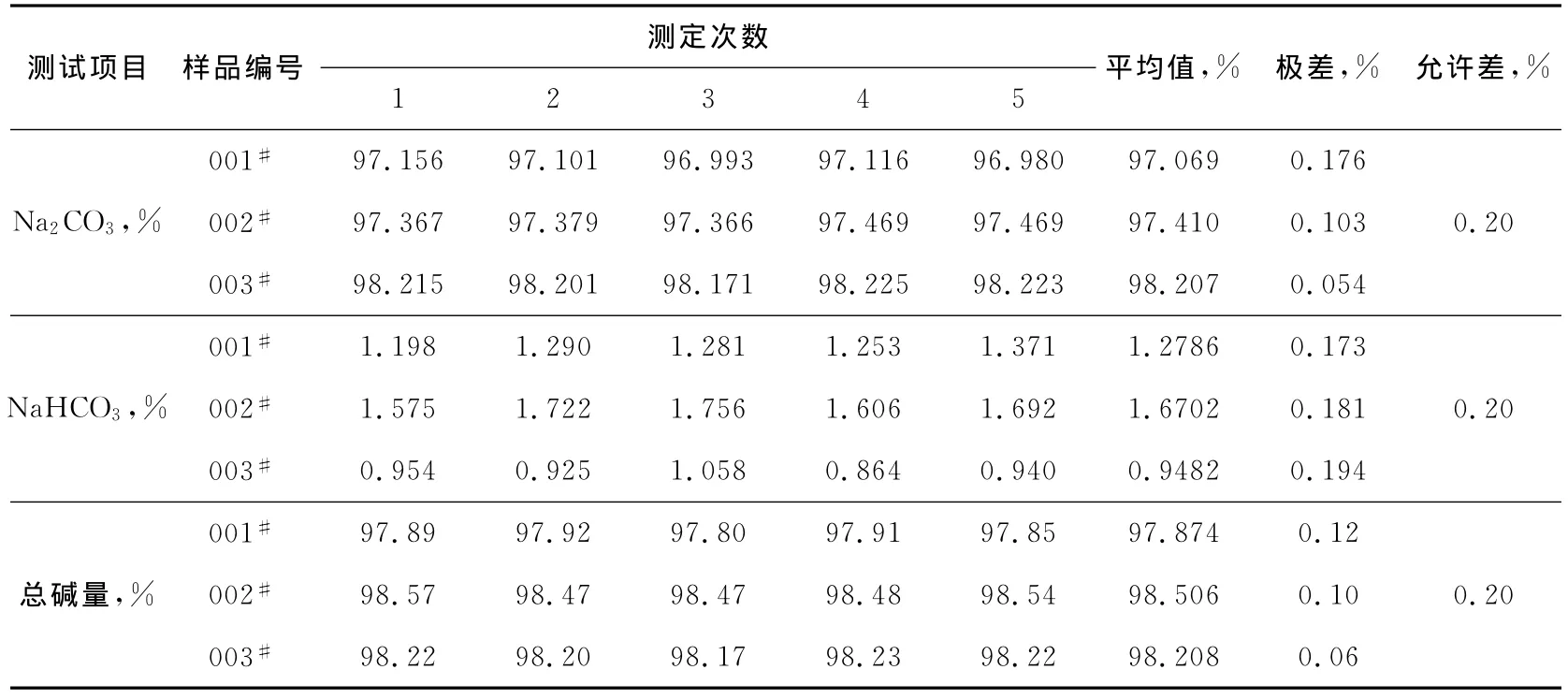
表5 电位滴定—线性神经网络法测试精密度考察表

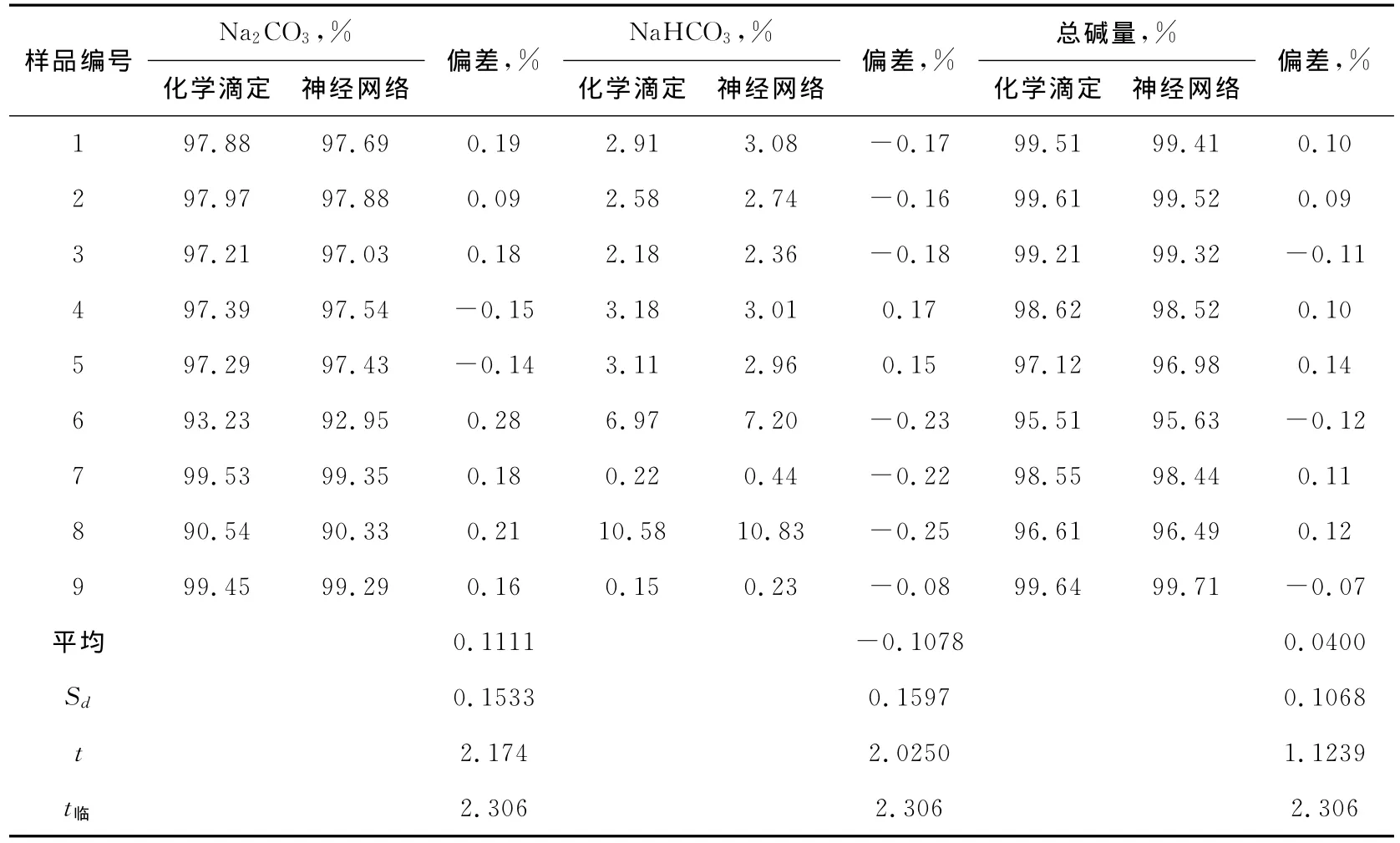
表6 化学滴定法与电位滴定—线性神经网络法测定的“对子”数据表

3 结 语

1）电位滴定—线性神经网络法同时测定碳酸钠中的碳酸钠和碳酸氢钠含量以及总碱量是可行的。

2）用化学滴定法和电位滴定—线性神经网络法，测试碳酸钠和碳酸氢钠含量以及总碱量，两种方法的测试结果经统计分析，有95%的把握认为两者无显著差异，即两者的测定结果吻合。

3）电位滴定—线型神经网络法，滴定时不一定使用标准溶液，只要网络训练、测试和预测用的溶液浓度相同即可，滴定完毕后无需计算，只要用训练好的网络对测试集样本或未知样本进行仿真预测，即可得到测定结果。较国标化学滴定法快速、方便，出现差错可能性大大降低，同时耗用试剂少。

4）实践表明，电位滴定—线性人工神经网络法，在大批量试样测试时更有优势，因此在工业碳酸钠生产过程控制分析中是一种可供选择的好方法。

［1］ GB／T210.2—2004，工业碳酸钠及其试验方法，第二部分：工业碳酸钠试验方法［S］.

［2］ 姚小红，张涤，等.用电位滴定法测定工业用氢氧化钠中氢氧化钠和碳酸钠的含量［J］.现代科学仪器，2006（4），96～97

［3］ 付业伟.人工神经网络及在分析化学中的应用［J］.咸阳师范学院学报，2002（4），27～30

［4］ 刘珍.化验员读本化学分析（第四版上册）［M］.北京：化学工业出版社，2004，221～223

［5］ 许国根，许萍萍，谭宪林.MATLAB在化学中的应用［M］.西安：西安交通大学出版社，2005，145～175

［6］ 郑用熙编著.分析化学中的数理统计方法［M］.北京：科学出版社，1986，97～122

TQ 075.3；TQ 114.1

A

1005－8370（2012）06－13－05

2012－08－04

叶芝锋（1974—）男，广东省化学工业学校，工业分析，化工助理工程师，分析工技师；现为广东南方碱业股份有限公司生产技术部分析员。