铝电解槽电阻信号的小波包分析

张 愉， 齐美星

(1.苏州市职业大学 电子信息工程系， 江苏 苏州 215104;2.苏州工业园区职业技术学院 机电工程系， 江苏 苏州 215021)

电解槽是炼铝的主要设备，具有高温、强腐蚀、强电磁场，变量之间强耦合等特点，可在线连续测量的信号只有槽电压和系列电流.因此计算出的槽电阻信号是唯一能够在线获得的反映槽况的参数[1]，也是实现电解槽自动控制(主要指氧化铝浓度控制、阳极效应预报控制和温度热平衡控制)的关键变量[2-4].因此，对槽电阻信号进行更精细的分析，有助于更好地掌握电解槽的运行状态.

传统的傅里叶变换将信号的时域和频域特征联系起来，能较好地刻画信号的频率特性，但是傅里叶变换是一种全局的变换，要么完全在时域，要么完全在频域，不能把两者结合起来.于是Dennis Gabor于1946年创立了短时(加窗)傅里叶变换，短时傅里叶变换虽然一定程度上克服了传统傅里叶变换没有局部分析的不足，但其也有自身的缺陷：窗口函数大小固定，时域和频域不可能同时都有高分辨率.对于实际工程中经常出现的非平稳信号，尤其是突变信号的描述和瞬时特性的分析，傅里叶变换和短时傅里叶变换都难以胜任，本文提出小波包分析，它是傅里叶分析思想方法的发展和延拓.

小波包(wavelet packet)可以对信号进行更精细的分析，与多分辨率分析不同之处就是它对每一层高频部分和低频部分都进行进一步分解，并能够根据被分析信号的特征，自适应地选择相应频带，使之与信号的频谱相匹配，从而大大提高了信号的时域和频域的分辨率.本文以某铝厂300 kA电解槽为研究对象，通过现场采集大量的阳极效应前和正常期的槽电阻试验数据[5]，采用小波包分析方法，提取信号的变化特征，从而为提前作出阳极效应预报提供可能.

1 槽电阻信号预处理

数据预处理是分析信号前非常重要的一个步骤，它可以剔除干扰及异常数据，提高信号分析的准确性.由于受电源质量、整流装置、电解槽规模、人工作业以及阳极效应等因素影响，电解槽系列电流会发生波动，相应槽电压也会变化.因此对于电解槽的控制，一般都采用槽电阻R，

(1)

式中：U为槽电压；E为反电动势(一般为常数)；Uman表示工艺控制需要而由控制系统或人工设定的电压变化量；I为系列电流.

原始的槽电阻信号主要包括：

1) 环境电磁干扰和采样噪声.在检测系统的硬件方面做好抗干扰措施，如进行电气隔离、使用屏蔽双绞线或传输线外套上金属管、正确地接地，硬件滤波等；软件上再进行相应的数据预处理，基本上可以将这部分噪声降低到最小程度.

2) 有用噪声.经过多次观察测试发现，这部分信号与电解槽的槽况有直接的关系，而且不同槽况对应不同的频率段信号.如由于槽底沉淀或碳渣多，在电磁力的作用下，或电流分布不均引起的铝液涌动，会明显地反映到槽电阻有规律地波动，波动周期一般为25～80 s(如图2虚曲线所示)；另外阳极的工作状态也会反映到槽电阻信号的高频变化中.

3) 有用的低频信号.这部分信号主要反映电解槽极距和电解质状况，当槽况稳定时，很大程度上就反映了电解液中氧化铝浓度大小.

图1即为某铝厂电解槽系列现场，图2为一组原始槽电阻信号样本.

图1 铝电解槽系列 图2 槽电阻信号样本

(2)

进行数字离散化，最后整理得到数字滤波算法为

RL(n)=0.001 312RS(n)+0.003 936RS(n-1)+0.003 936RS(n-2)+0.001 312RS(n-3)+

2.787 52RL(n-1)-2.610 1RL(n-2)+0.810 47RL(n-3),

(3)

式中：RS(n)，RS(n-1)，…，RS(n-3)表示槽电阻本次及前几次原始采样值；RL(n)，RL(n-1)，…，RL(n-3)表示本次及前几次滤波后的槽电阻值.

2 槽电阻信号的小波包分析

2.1 小波包分析

小波包分析可以对信号进行更精细的分析.也是对频带进行多层次划分，而且对每一层信号的高频和低频部分都进行进一步分解，并能够根据被分析信号的特征，自适应地选择相应频带，从而提高了信号的时频域的分辨率[6-7].以四层小波包分解为例， S表示待分析信号，S10表示第一层分解的低频部分，S11表示第一层分解的高频部分.对于第二层,S20表示S10分解的低频部分，S21表示S10分解的高频部分[8].依此类推，直至分解到第四层，因此可表示为S=S40+S41+S42+…+S415.四层小波包分解树如图3所示.

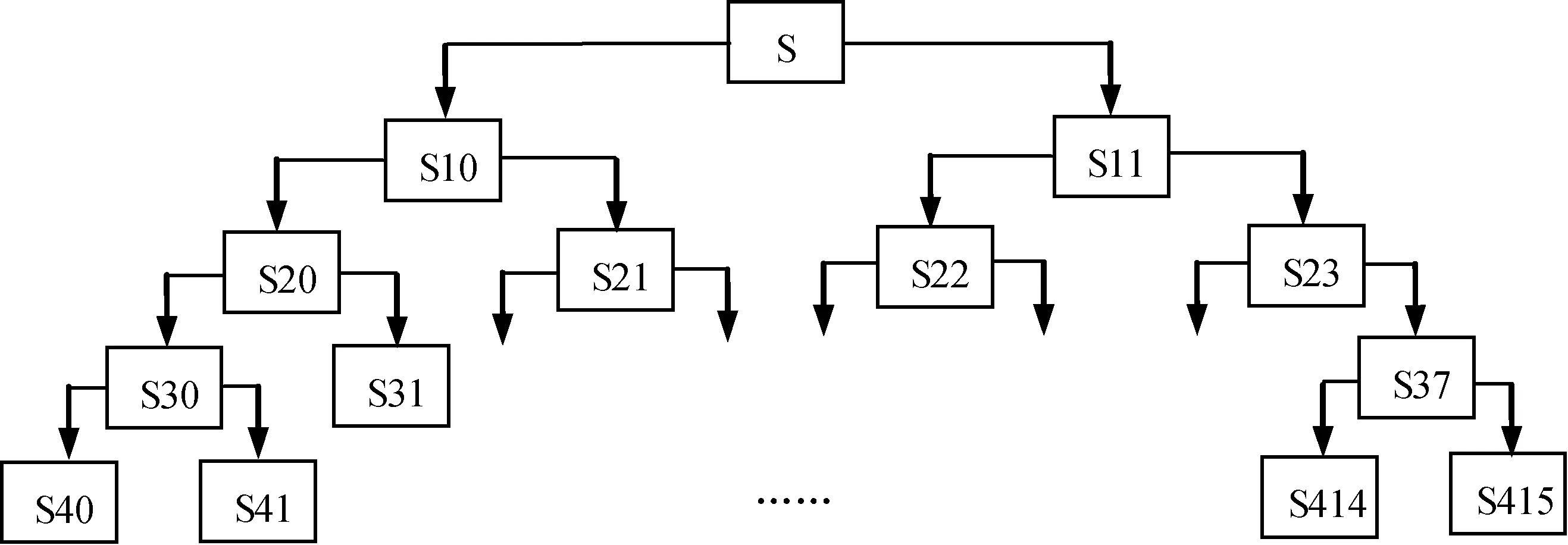
图3 四层小波包分解树

(4)

(5)

g(k)=(-1)kh(1-k).

(6)

式(6)表示系数具有正交性.由式(5)构造的序列{un(t),n∈Z且n≥0}称为由基函数u0(t)=φ(t)确定的正交小波包.由于φ(t)由hk唯一确定，故又称{un(t)}关于序列{hk}的正交小波包.

小波包的分解算法为

(7)

(8)

2.2 槽电阻信号的小波包分析

从生产现场采集了电解槽连续运行2个多月的系列电流、槽电压和槽电阻的原始数据.对槽电阻数据进行如下取样：

1) 阳极效应前的槽电阻序列.取每次效应发生前45 min以内的数据,以TS(取3 min)间隔进行分段Ri j(i=1,2,…,51；j=1,2,…,15)，i表示第i次效应,j表示第j个时间段.这样共有51×15=765组数据，为了简化分析又不失一般性，从每次效应前的数据组中分别随机选出10组，得到共40组效应前的电阻序列RAE i(i=1,2,…,40).

2)正常期的槽电阻序列RNBi(i=1,2,…,40).从正常期(一般认为效应发生前2 h以上和效应后1 h以上且非人工作业期如换阳极，出铝等)的数据中随机选出40组，每组数据的时间长度也取TS.

根据理论分析和实际观察发现，反映电解槽槽况的电阻信号变化是相当缓慢的，而阳极状况引起的槽电阻高频成分的频率一般也不会超过1 Hz，所以原始信号采样周期定为200 ms，这样足以保证不丢失信号的成分.为了更精细地刻画槽电阻高频信息，采用小波包分析槽电阻信号.同时为有效提高各通道滤波的频带选择性，降低信号在不同频带上的串扰，采用了八阶Daubechies小波.四层小波包分解及重构信号见图4.

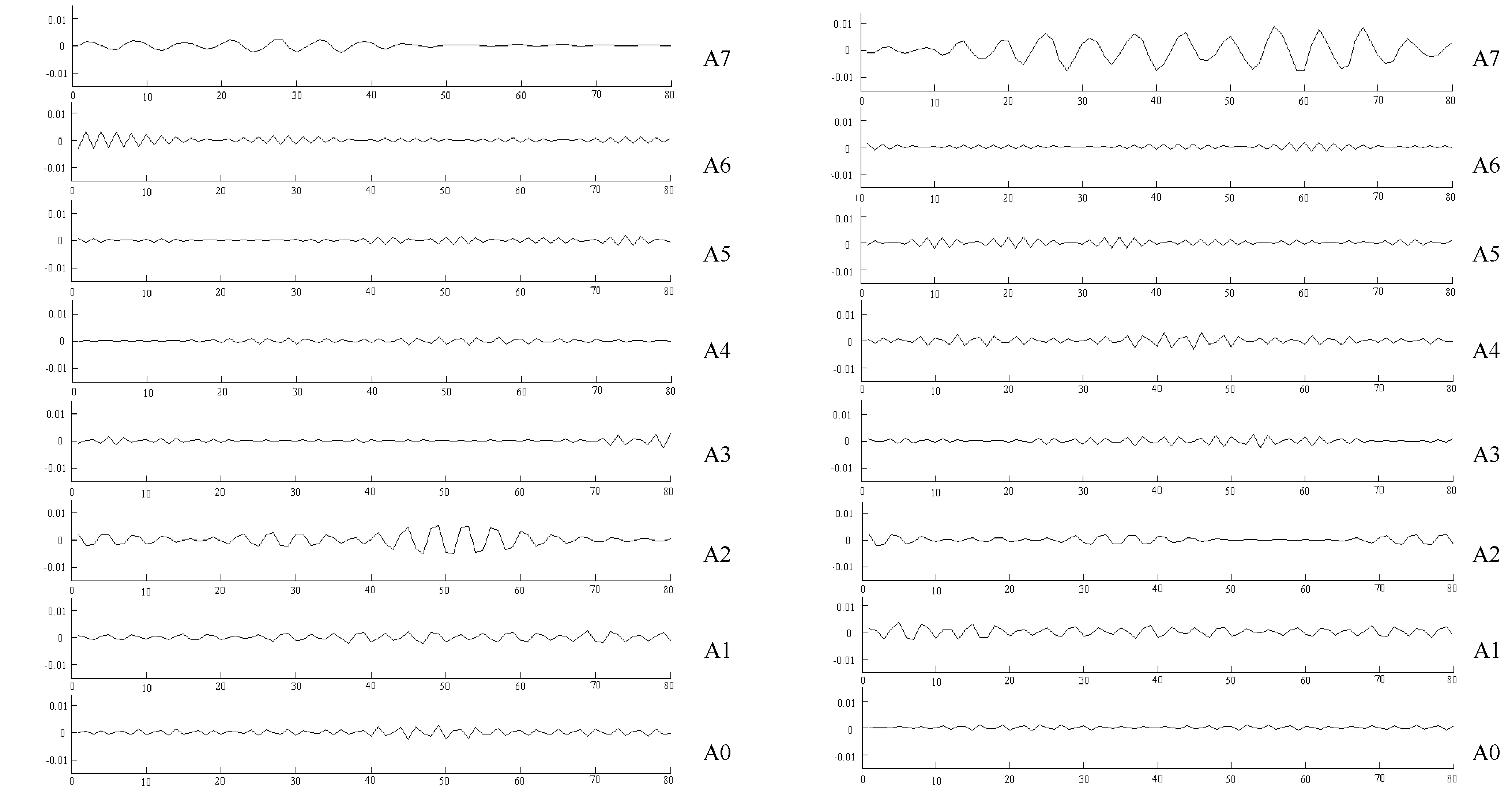
(a) 正常期 (b) 效应前图4 四层小波包分解及重构信号

图4(a)曲线表示正常期的槽电阻原信号及其四层小波包分解后的第四层各系数重构信号，图4 (b)曲线表示两组效应前的槽电阻原信号样本RAE i及其四层小波包分解后的各系数重构信号.A0表示原始槽电阻信号；A1为第四层小波包分解后的低频部分，相当于图3中的S40的重构信号；A2～A15为小波包分解后的各小波系数，相当于图3中的S41～S414的重构信号.从曲线中大致可以看出，在各个小波重构信号中，正常槽况下的槽电阻高频部分不是很明显，而效应前的槽电阻对应于S41、S43和S47等三个高频小波段明显增大,如图4 (b)所示.大量的仿真试验也验证了这一推断.

3 槽电阻的特征向量提取

由前面的小波包分解理论可以知道，小波包分解的实质就是将信号向各个正交基上投影，经过N层分解的小波包，信号的能量被分解到2N个正交频带上，且信号在该层上各个频带内的能量总和应该等于原信号的能量.

为了方便分析和描述效应发生前的槽电阻的信号，以上面的槽电阻四层小波包分解为例，采取如下的构造特征向量方法(由于本试验只关心槽电阻信号的高频部分，所以没有将低频部分纳入特征向量中)：

1) 对于频带信号S4i, (i=1,2,…,5),其能量定义为

(9)

式中：wij为信号S4i小波系数序列的第j个分量；n表示信号S4i小波系数序列总数.

2) 频带信号S4i的小波分解系数的模为

(10)

3) 由上面可以看出，信号频带的能量等于小波系数的模的平方，因此用小波系数的模构造信号的特征向量是合适的，可以构造为T=[MS41,MS42,…,MS415].

按照上面的特征向量构建方法,对40组效应前的槽电阻信号和40组正常期的槽电阻信号分别提取其特征向量，如表1所示(为避免前面所述的边界溢出现象带来的影响，实际计算时忽略小波系数前后两端的两个值，限于篇幅，表中只列出了其中的10组).为了更清晰地反映特征向量能否描述槽电阻信号，取两个特征向量Ti和Tj之间的欧氏距离为

(11)

计算出的特征向量间的欧氏距离如表1所示，可以清楚地看出：对于同类型(效应前的槽电阻信号或者正常期的槽电阻信号)的特征向量间的距离较小，而不同类型的特征向量间的欧氏距离都比较大，即不同类型的特征向量区分度大.这说明通过上述方法构建的特征向量描述效应前的槽电阻信号的特征是合适的.

表1 特征向量间的距离

4 结论

从阳极效应(anode effect)的发生机理来看，阳极效应的发生是一个从开始孕育、不断发展到最后发生的

过程，这一特殊的槽况在可测的电解槽信号中应该有所反映.本文将小波理论应用到槽电阻信号的分析中，通过采集大量的试验数据样本，将槽电阻信号进行四层小波包分解，发现阳极效应发生前和正常槽况下的槽电阻信号有所不同，信号的高频成分增加.建立的特征向量可以很好地反映阳极效应前槽电阻信号的变化特征，这为提前作出阳极效应预报及控制提供新的途径.

参考文献：

[1] 李届家.铝电解生产过程中阳极效应预报新方法研究[J].轻金属, 2002,34(1):25-27.

[2] ARTHUR J.Wavelet packet timeseries analysis of aluminum electrolytic cells[C]//The International Society for Optical Engineering. Orlando: IEEE Computer Society Washington, 2001.

[3] STANISLAW P.The effect of anode-cathode distance on the electrical bath resistivity in alumium electrolysis with insert anodes[J].Erzmetal, 2008,61(6):1021-1029.

[4] ZHU Hong min, THONSTAD J. Anode reaction in aluminum electrolysis prior to and during anode effect[C]//The 132ndTMS Annual Meeting:Light Metals. San Diego California: IEEE Computer Society Washington, 2003:5-8.

[5] THONSTAD J. Anode reaction in aluminium electrolysis prior to and during anode effect[J]. Light Metals, 2003, 35(4):343-349.

[6] MALLAT S. A theory for multi-resolution signal decomposition the wavelet representation[J]. IEEE Transation on Pattern Analysis and Machine Intelligence, 1989,11(7):674-693.

[7] SAKSVIKROENNING T, VEE K. Estimation of states in aluminium reduction cells applying extended kalman filtering algorithm together with a nonlinear dynamic model and discrete measurements[J].Light Metals, 1996,28(1):275-287.

[8] METSON J B, HYLAND M, CHEN Jing xi. The anode effect revisited proceedings of sessions[J].TMS Annual Meeting (Warrendale, Pennsylvania), 2002,12(3):239-244.