傅里叶变换在信号设定门限分解中的应用

陶志福， 姚 萌

(1.苏州市职业大学 电子信息工程系， 江苏 苏州 215104; 2.华东师范大学 电子工程系， 上海 200062 )

目前BRATUMASS[1]系统采样信号分析中存在以下两方面的问题：一是采样信号中伴生有大幅度的发射信号成分,而有效回波信号相对于伴生信号来说能量幅度很小，其谱线可能出现在采样频谱的任何区域，用常见的滤波方法往往也削减了本来很弱的有效回波信号成分;二是以BRATUMASS系统采样信号为基础的目标特性计算是以目标空间背景散射为基础，但背景散射本身又是弱小有效信号中最弱的，以何种准则来判定一个弱小的信号分量就是背景散射，即从很弱的有效回波信号中确定更弱的背景散射成分，这是BRATUMASS系统能否进行后续工作的关键.

对于信号的分解，考虑到实际信号采样总是持续有限的时间，而BRATUMASS系统采样信号经归一化处理后总能满足弱函数[2]的性质.也就是说可以按照弱函数的理论用Hermite基函数展开[2]，即有

(1)

存在，式中φn(x)为Hermite基函数.进而有

(2)

相应的信号f(x)的傅里叶变换可表示为

(3)

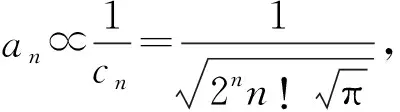
而另一方面对于背景散射信号频率分量，本文意在从频谱幅度的概率统计的角度进行探讨，提出一种基于频谱幅度分布的下限提取方法.

1 信号强弱分量分离模型

对信号进行分解的方法有很多，如小波分解方法[3]、经验模式分解[4]等.2004年，Roebel等提出针对语音信号的谱峰，从信号的时频分布的特性中寻找对其进行分类的信号分解方法[5].该方法可以很好地分离语音信号中的噪声和有效语音成分.本文将从信号频谱幅度划分的角度，构建序列探讨信号分解的途径.为BRATUMASS系统数据后期图像分层重建从信号分离机制上提供可行的技术途径[6].

1.1 信号在频谱幅度门限afloor下的强弱分解

若信号f(t)的傅里叶变换频谱F(ω)幅度可被某一门限afloor划分为两部分.其中高于门限afloor的频谱为FaH(ω)，剩下的频谱为FaR(ω).则显然有

F(ω)=FaH(ω)+FaR(ω)，

(4)

从而有

f(t)=faH(t)+faR(t)，

(5)

式中：faH(t)为对应于FaH(ω)的逆傅里叶变换；faR(t)为对应于FaR(ω)的逆傅里叶变换.

faR(t)=faRH(t)+faRR(t)，

(6)

于是有

f(t)=faH(t)+faRH(t)+faRR(t).

(7)

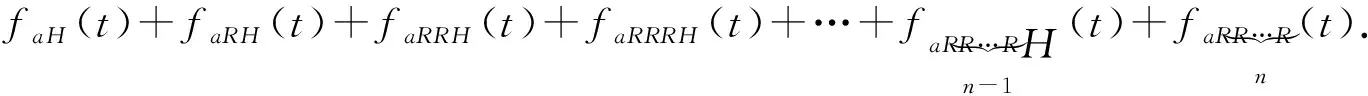
(8)

1.2 序列的选择

2 基于信号频谱幅度概率分布的提取

设信号s(t)对应的傅里叶变换的归一化频谱函数为S(ω)，在频率和归一化幅度坐标系内，将S(ω)改写为二维函数形式S(ω,p)，其中p是对应的幅度坐标.考虑所有的频率谱线的幅度分布ρ(p)，应有

(9)

(10)

图1 噪声信号的功率谱和频谱幅度概率分布图

由信号分析的理论可知，实际信号总是可以看作是有效信号和噪声的叠加.即s(t)=s0(t)+N(t)，其中：s(t)是实际信号；s0(t)是其中有效信号成分；N(t)是混在其中的噪声.容易推得

ρs(t)(p)=ρs0(t)(p)+ρN(t)(p)，

(11)

其中：ρs(t)(p)是s(t)信号对应的ρ(p)分布；ρs0(t)(p)是s0(t)信号对应的ρ(p)分布；ρN(t)(p)是N(t)信号对应的ρ(p)分布.

(a) 合成信号的功率频谱 (b) 合成信号的(p)-ρ图图2 合成信号s(t)的功率谱和频

3 实际数据计算

3.1 实际信号强弱分量的分离

当使用式(5)将信号进行强弱分量分离到一定程度时，余量中弱小的有效信号往往会隐藏于随机噪声之中.这时需要对弱小信号的下限进行提取.下面对某一病例第四点采样信号进行分解.图3为该采样点实际采样信号.

图3 第四采样点实际采样信号

图4是用门限序列为0.38,0.382,0.383,0.384,0.385，进行5次分离后得到各个信号，其中f(t)=fa1H(t)+fa2H(t)+fa3H(t)+fa4H(t)+fa5H(t)+fa5R(t)，fa1H(t)对应于式(8)中的faH(t)，fa2H(t)对应于式(8)中的faRH(t)，…，fa5H(t)对应于式(8)中的faRRRRRH(t)，fa5R(t)对应于式(8)中的faRRRRRR(t).从图4中可以看出在该设定门限序列的划分下，信号的广义函数构成情况，即该采样时刻回波信号冲击到达合成情况，对应同种性质的目标回波在信号采样时段内的合成情况.从图4中可以看出在横坐标1 000～1 500之间有多重冲击存在，即该延时对应位置上有多种特性组织界面存在.该点采样信号的db3小波5层分解的结果显示如图5所示，仅d3层可以检测出来明显的冲击，其他层的冲击分离不太明显，也就是说界面有效回波的特征在小波分解中并不能非常有效地显示出来.

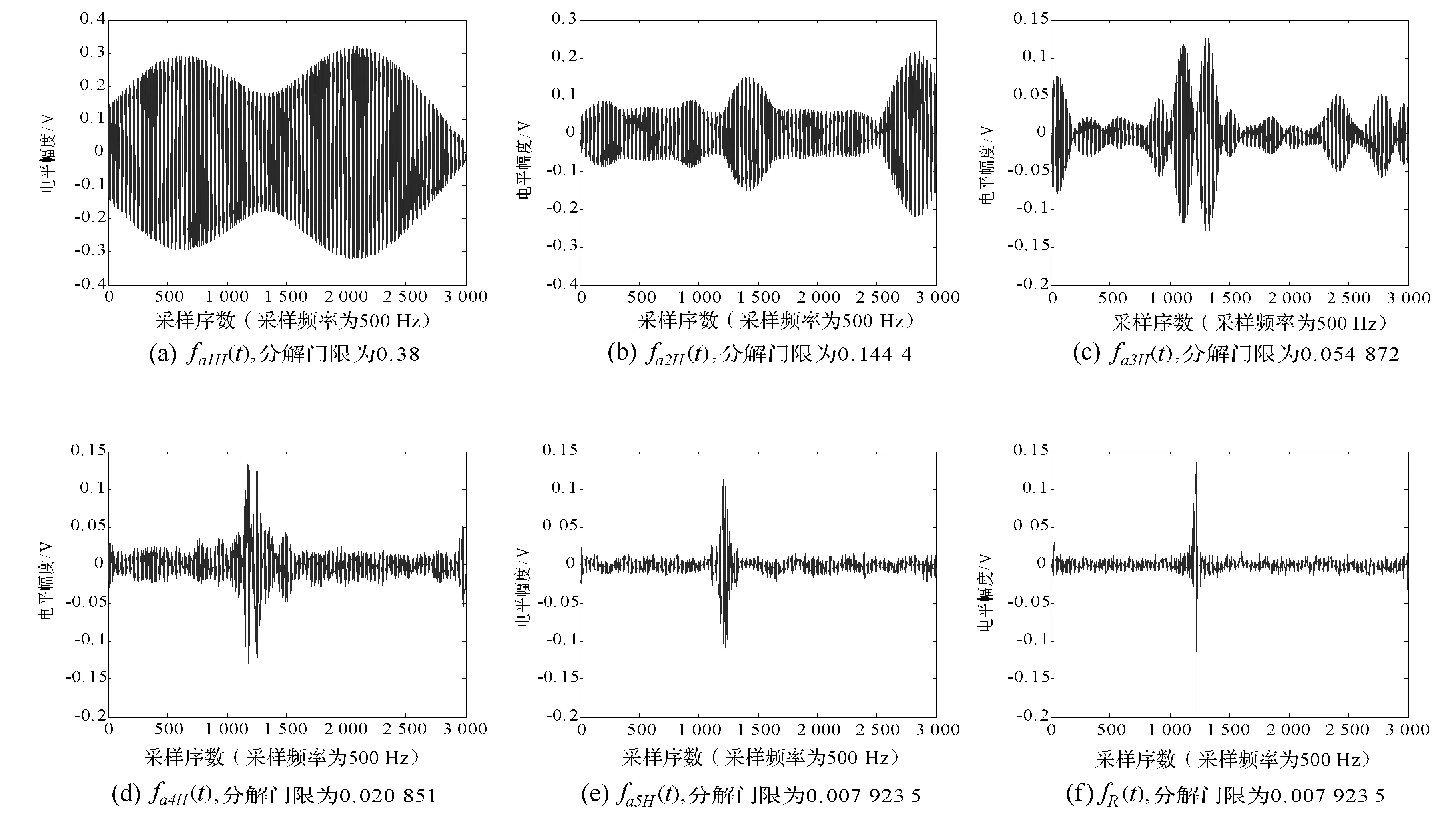
图4 用门限序列为0.38、0.382、0.383、0.384、0.385，进行5次分离后得到各个信号

3.2 实际信号有效成分下限的确定

将图5中第5层余量fa5R(t)的ρ(p)分布和随机噪声rand(t)的ρ(p)分布进行对比，其结果如图6所示.可以看出，在归一化幅度为0.149 7附近差异最大，换算到原先信号中对应为0.149 7×0.385=0.001 186.即回波有效信号的下限约为0.001 2.由回波比率和电磁特性值之间关系可知，在BRATUMASS系统环境下，其对应的回波辐射背景的目标特性参数约为10.05，其与实际BRATUMASS系统环境下正常乳腺组织的目标特性参数值10接近[7].

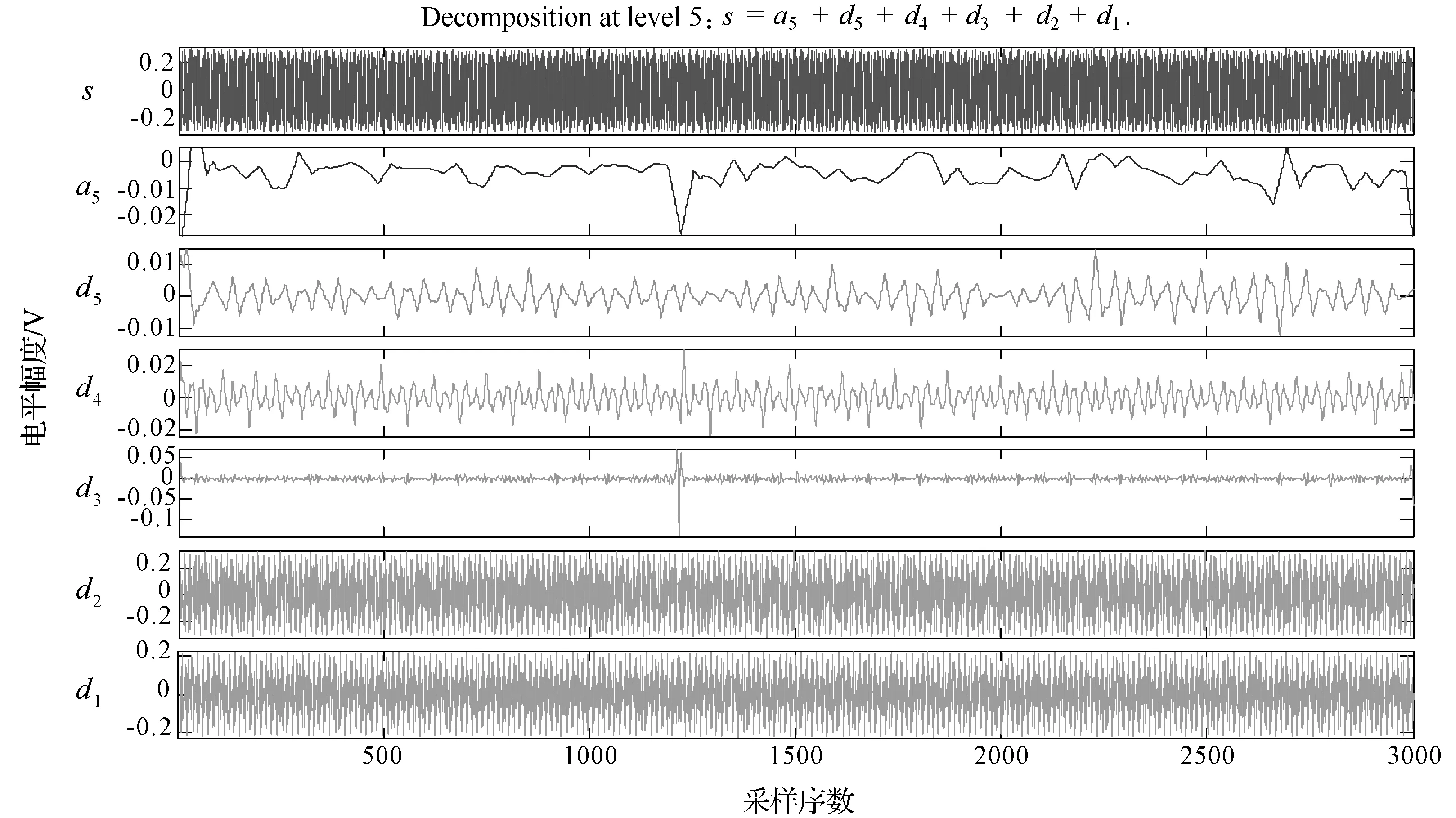
图5 第4采样点db3小波5层分解的结果

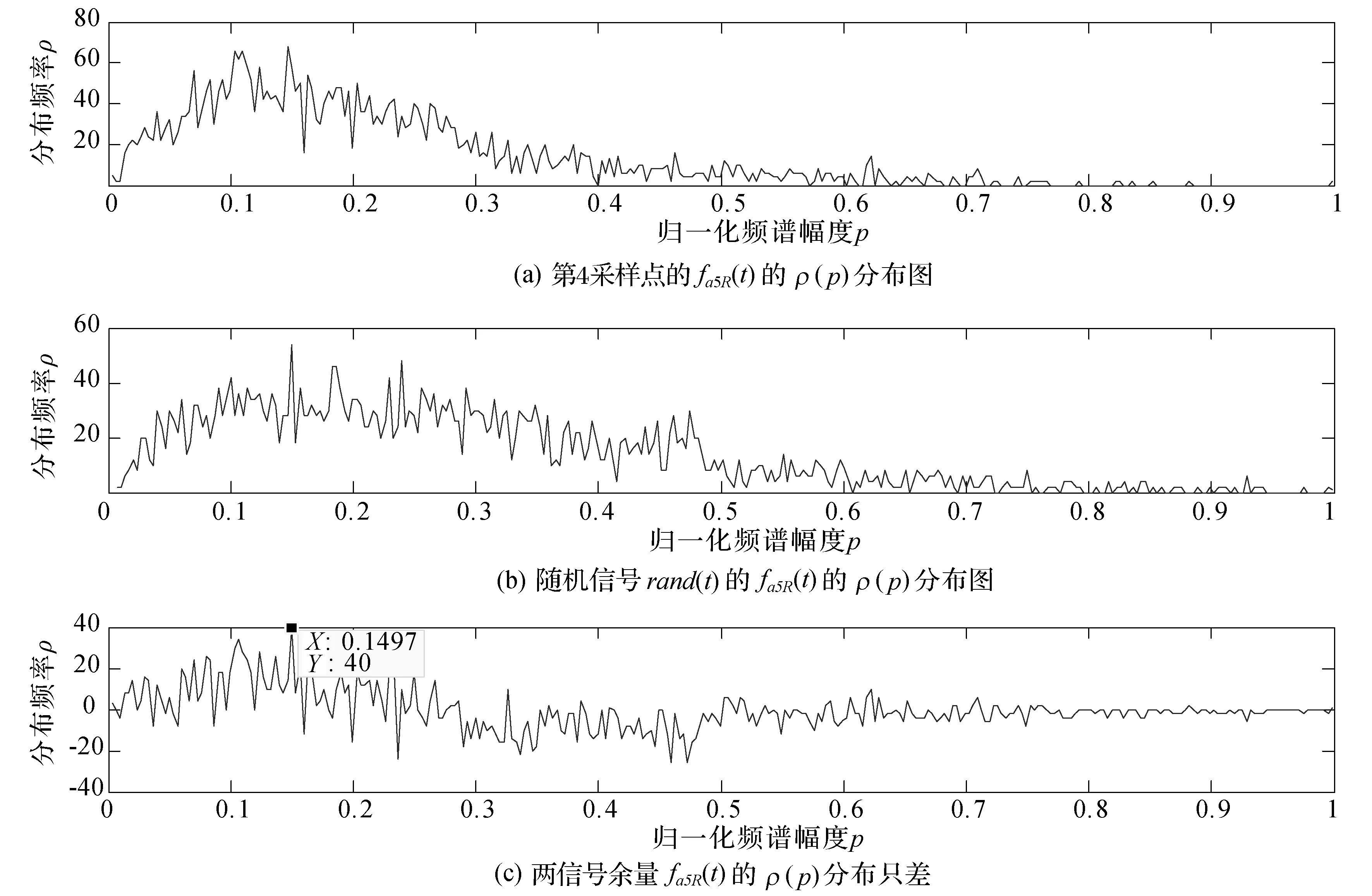
图6 第4采样点信号和随机信号rand(t)分解到第5层，其余量fa5R(t)的ρ(p)分布对比

4 结论

针对在BRATUMASS系统环境下，对其采样信号按照一定门限序列进行强弱分解.实际上是按照弱函数在Hermite基下的分解来考察同一幅度区间信号的合成情况.由于不同门限可以与不同特性的目标组织特性相对应，那么按照门限进行分解，实际上就是对目标组织按照特性进行分类.这有助于后期图像按照组织分层进行显示.而基于信号频谱幅度概率分布的分离背景散射信号提取方法则是考虑到分离模型不可能进行无穷次分离而提出的.从实际应用效果来看，可以找出与实际特性值接近的背景散射分量的幅度，然而由于系统受限于采样精度等因素影响，目前下限分离很难达到0.001以下，有待于系统进一步改进.

参考文献：

[1] ZHI Fu-tao, XIA Cheng-dong, MENG Yao. The electromagnetic-trait imaging computation of traveling wave method in breast tumor microwave sensor system[J]. Software tools and algorithms for biological systems-advances in experimental medicine and biology, 2011, 696(6): 489-495.

[2] 丁夏畦,丁毅. Hermite展开与广义函数[M].武汉:华中师范大学出版社,2005:30-62.

[3] MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation[J].Pattern Analysis and Machine Intelligence, 1989 ，11 (7): 674-693.

[4] HUANG N E.The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis [J]. Proc. Roy. Soc. London, 1998,454: 903-995.

[5] REBEL A, ZIVANOVIC M, RODET X. Signal decomposition by means of classification of spectral peaks [C]//in Proc. of the International Computer Music Conference (ICMC’04), Miami, Florida, 2004:446-449.

[6] 董夏晨,陶志福. 微波近场乳腺癌探测数据处理终端[J]. 科技创新导报, 2011(3): 216-217.

[7] 陶志福,潘琪峰. 基于微波探测数据反演空间介电常数分布的实验仿真[J]. 苏州市职业大学学报,2009,20(4):9-11.

[8] 张会生, 陈树新. 现代通信系统原理[M]. 北京:高等教育出版社, 2009:35.

[9] SHELDON M R. 随机过程[M].何声武，译.北京：中国统计出版社,1997: 12-13.