高速铁路连续屏障减振效果分析
刘 腾,雷晓燕
(华东交通大学铁路环境振动与噪声教育部工程研究中心,江西南昌330013)
近年来随着我国铁路向高速、重载方向的快速发展,由此而带来的沿线环境振动问题日益严重,特别是一些既有线路的提速,以及重载货物列车的投入使用,进一步加剧了沿线环境振动的影响。国际上已把环境振动列入国际七大公害之一[1],并已开始着手研究振动污染规律、振动产生的原因、传播路径与控制方法以及对人体的危害等问题。
关于轨道交通系统诱发的环境振动,国内外学者利用各种方法进行了大量研究。雷晓燕和圣小珍[2]通过改进车辆、轨道结构等措施来分析减振效果,从其研究成果来看,结合具体工程状况,通过有效措施控制振动能量和噪声的主频范围来到达减振降噪的效果。Kani和Hayakawa[3]将高架桥沿线的管桩作为屏障隔振来研究,并结合现场测试结果和有限元方法,验证了管桩隔振措施不管对地表还是大地内部都具有减振效果。高广运[4]和蔡袁强[5]在屏障减振措施上做了大量的理论和数值研究,得出不同屏障形式在饱和土体和非饱和土体中的隔振效率。Takemiya[6]分别用边界元法和有限元法分析了波阻板(WIB)屏障的隔振效果。Peplow[7]通过边界积分方程方法,分析了双层地基WIB屏障的隔振效果。
1 移动荷载的模拟
采用傅里叶变换的方法求解轨道结构连续弹性三层梁模型得到路基面上的动荷载[8-9],模型如图1所示,第一层梁为钢轨,简化为连续支撑的欧拉梁,第二、三层分别为轨枕和道床,简化为离散质量结构,则其振动微分方程如式(1)~式(3)。其中车辆结构参数采用和谐号高速动车CRH3参数,轨道结构参数采用博格板式轨道结构参数,轨道不平顺模拟采用美国六级谱,求解得到路基动荷载如图2所示。
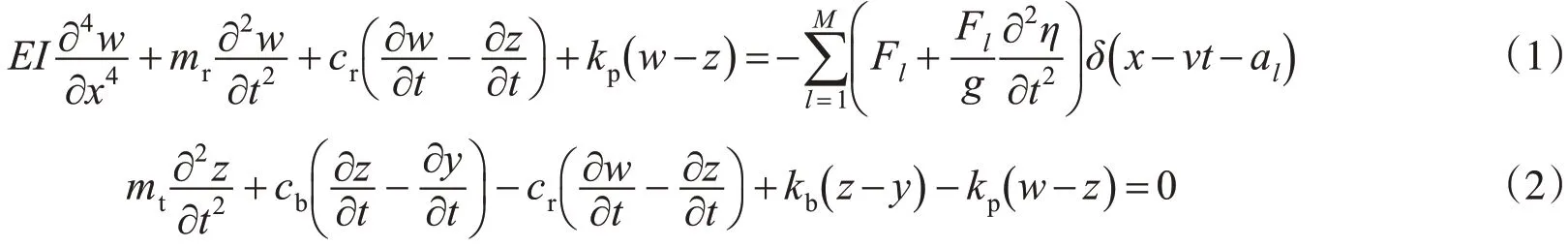

式中:w,z和y分别为钢轨、轨枕和道床竖向挠度;mr,mt和mb分别为单位长度的钢轨质量、轨枕质量和道床质量;kp,kb和ks分别为单位长度轨枕垫板和扣件刚度、道床刚度和路基等效刚度;cr,cb和cs分别为单位长度轨枕垫板和扣件阻尼、道床阻尼和路基等效阻尼;δ为Dirac函数;v为列车行驶速度;Fl为第l个轮载;t=0 时轮载至原点的距离为al;轮载总数为M;轨道随机不平顺值是η(x=vt)。

图1 轨道结构三层梁模型Fig.1 Three elastic layers of track structure

图2 v=200 km·h-1时路基荷载时程Fig.2 The subgrade dynamical load changing with time(train speed=200 km·h-1)
2 计算模型及材料参数
采用大型通用有限元软件ANSYS 建立路基—大地耦合模型,边界处理采用三维一致黏弹性人工边界条件[10-11],具体的三维模型尺寸见图3。宽度为80 m、长度为80 m、深度为65.5 m。选取的单元都为solide45,土层和路基参数选取如表1 所示,则单元尺寸沿深度方向其每层土的单元尺寸依次为:1,1.5,1.5,2.5 m;长度和宽度方向取为2 m。时间步长选为0.005 s。

图3 大地有限元模型Fig.3 The finite element model of ground

表1 模型参数Tab.1 Model parameters
3 计算结果及分析
按照我国的城市区域环境振动标准GB10070-1988规定,采用ISO2631的1/3倍频的计算方法,得出地面振动加速度级(简称振级)。振动加速度级La是根据各中心频率的有效值按照下面公式计算得到:


式中:La为振动加速度级,dB;a0为基准加速度,取值为10-6m·s-2;a为振动加速度有效值,m·s-2;af表示频率为f的振动加速度有效值,m·s-2;cf为振动加速度对应不同频率的感觉修正值[12-13]。
3.1 空沟隔振效果分析
考虑CRH3列车行驶速度为200 km·h-1时引起的大地振动,将固定宽度为2 m的空沟分别设在距轨道中心线14 m处和18 m处,得出深度分别为2,5,8 m和10 m沟屏障的减振效果。

图4 不同的屏障深度,最大Z振级随距离变化情况Fig.4 The maximum Z weighted vibration acceleration level changing with distances under different depths of barriers
由图4可知:
1)当不设置屏障时,最大Z振级曲线平缓的下降,说明高速列车引起的环境振动级是随距轨道中心线距离的增加成逐渐下降的趋势;当设置屏障时,最大Z振级曲线明显下降,主要是屏障起到阻隔振动波的传递效果。
2)对于深2 m的屏障,其隔振效果值在1 dB左右;深5 m的屏障其隔振效果值在2.5 dB左右;深8 m的屏障其隔振效果值在4 dB左右;深10 m的屏障其隔振效果值在4~5 dB之间。说明空沟隔振的效果是随沟深的增加而增加,但深度增加到一定时,继续增加屏障深度其隔振效果并不会明显增加。
3.2 填充沟隔振效果分析
考虑CRH3列车行驶速度为200 km·h-1时引起的大地振动,将固定宽度为2 m的混凝土填充沟设在距轨道中心线14 m处,得出深度分别为5,10 m和15 m沟屏障的减振效果。
从图5可以看出:
1)当混凝土填充沟设置在距轨道中心线14 m处时,其隔振效果是随沟深的增加而增加;各考察点随距轨道中心线距离的变化,不同屏障深度的隔振效果基本上都是随距离的增加其隔振效果逐渐减弱。
2)从减振值图来看,对于深5 m的屏障,在距轨道中心线20~40 m范围内,其隔振效果值平均在1 dB左右,40 m以上范围内,其减振值递减到0.5 dB左右;深10 m的屏障在距轨道中心线20~40 m范围内,其隔振效果值平均在2.5 dB左右,40 m以上范围内,其减振值递减到1 dB左右;深15 m的屏障在距轨道中心线20~40 m范围内,其隔振效果值平均在4 dB左右,40 m以上范围内,其减振值递减到1.5 dB左右。
考虑CRH3列车行驶速度为200 km·h-1时引起的大地振动,将固定深度为10 m的混凝土填充沟设在距轨道中心线14 m处,得出沟宽分别为2,4 m和6 m沟屏障的减振效果。
从图6可以看出:混凝土填充沟设置在距轨道中心线14 m处时,沟宽的增加对其隔振效果的改善并不明显,所以一般我们设置屏障隔振时,首先应确定屏障的宽度,再考虑屏障其它关键因素,来达到屏障的最理想隔振效果。

图5 不同的屏障深度,最大Z振级随距离变化情况Fig.5 The maximum Z weighted vibration acceleration level changing under distances under different depths of barriers
3.3 填充材料隔振效果分析
为了比较不同填充材料的隔振效果(见表2),考虑CRH3列车行驶速度为200 km·h-1时引起的大地振动,填充沟位置设置在距轨道中心线14 m处,其沟深10 m,沟宽为2 m。

表2 填充材料属性Tab.2 Filling material attributes
由图7可知,不同材料的减振效果,空沟的减振效果最好,泡沫、橡胶次之,混凝土隔振效果良好,细砂材质其减振效果值并不明显;说明填充沟材料的阻抗与土体的阻抗比值相差越大,其隔振效果就越好,反而与土介质属性比较接近的砂石,其隔振效果不理想。

图6 不同的屏障宽度,最大Z振级随距离变化情况Fig.6 The maximum Z weighted vibration acceleration level changing with distances under different widths of barriers

图7 不同的屏障填充材料,最大Z振级随距离变化情况Fig.7 The maximum Z weighted vibration acceleration level changing with distances under different material barriers
4 结论
1)屏障隔振的效果是随屏障深度的增加而增加,但当屏障增加到一定时,即一倍瑞利波波长时,继续增加屏障深度,其隔振效果不会明显增加。
2)沟宽对屏障的隔振效果次于深度、位置对屏障的影响,则设计合理的屏障尺寸时,一般应先确定屏障的宽度。
3)填充沟屏障材料的选取对隔振效果至关重要,理想上选择波阻抗比系数远大于1或者远小于1的材料,对大地振动能量的阻隔越有效。
[1]高广运,孙雨明,吴世明.铁路产生的地面振动与减振[M]//李永盛,高广运.环境岩土工程理论与实践.上海:同济大学出版社,2002:64-72.
[2]雷晓燕,圣小珍.铁路交通噪声与振动[M].北京:科学出版社,2004:81-90.
[3]KANI Y,HAYAKAWA K.Simulation analysis about effects of a PC wall-pile barrier on reducing ground vibration[C]//Proceedings of the Thirteenth International Offshore and Polar Engineering Conference,Honolulu:Hawaii,2003:677-682.
[4]GAO G Y,LI Z Y,QIU C H,et al.Three-dimensional analysis of rows of piles as passive barriers for ground vibration isolation[J].Soil Dynamics and Earthquake Engineering,2006,26(11):1015-1027.
[5]CAI Y Q,DING G Y,XUC J.Amplitude reduction of elastic waves by a row of piles in poroelastic soil[J].Computers and Geotechnics,2009,36(3):463-473.
[6]TAKEMIYA H,JIANG J Q.Wave impeding effect by buried rigid block and response of dynamically excited pile foundation[J].Structural Engineering/Earthquake Engineering,1993,10(3):149-156.
[7]PEPLOW A T,JONESC J C,PETYT M.Surface vibration Propagation over a layered elastic half space with an inclusion[J].Applied Acoustics,1999,56:283-296.
[8]雷晓燕.轨道结构动力分析的傅里叶变化法[J].铁道学报,2007,29(3):67-71.
[9]雷晓燕,圣小珍.现代轨道理论研究[M].2版.北京:中国铁道出版社,2008:28-33.
[10]刘晶波.波动问题中的三维时域粘弹性人工边界[J].工程力学,2005,22(6):46-51.
[11]谷音,刘晶波,杜义欣.三维一致粘弹性人工边界及等效粘弹性边界单元[J].工程力学,2007,24(12):31-37.

