常见群桩排列方式浅析

毛穗丰，康 东，王 宏

(中国水电顾问集团成都勘测设计研究院，四川 成都 610072)

1 前 言

当今连续刚构桥型修建得比较多，特别是跨度在100～200m时，只要地形条件合适，首选的桥型一般都是连续刚构。此类桥型，当桥墩不高时(一般在70m以下)，一般采用双肢薄壁墩；当桥墩在70m以上时，采用箱型整体式的比较多。但不管采用哪种桥墩形式，除了扩大基础外，比较常见的是采用承台加群桩的基础型式，且桩基的根数一般不小于4。当桩数为n2时，桩基一般按纵横向对称排列，即按n×n的形式排列；但若不满足时，其排列方式则值得研究。以下主要介绍此类群桩的排列方式。

2 群桩的排列方式

群桩指在水平外力作用平面内有一根以上的桩的桩基础，群桩多与承台固结为一整体，共同受力。常见的群桩一般均有4根及以上的桩，其排列的方式也有多种，有纵横直线排列的，也有梅花形布置的。具体布置形式见图1(由于7根桩的形式很罕见，故图中未示此布置)。

以上几种常见的群桩排列方式，其共同点是桩基及承台均关于x轴与y轴对称布置，不同点是A、B、E排列由于承台为正方形，桩基排列完全对称(此时假定xi=yi)，此种情形比较简单，不再过多论述。但是当桩基承台为C、D特别是常见的C中(1)、(2)与D中(3)、(4)布置时，此时由于承台长边较短边长得多，桩基的排列就值得探讨了。

3 承台桩基竖直力计算

为了研究以上桩基承台中群桩的排列采用C中(1)与(2)以及D中(3)与(4)哪种更为合理，即在相同的前提条件下，哪种群桩的布置方式使桩基产生的最大竖直力更小，即认为是更合理的，这样在桥梁的设计中可减短桩长，降低桥梁造价。为此，先来探讨桩基竖直力的计算。计算图示见图2，计算公式见式(1)。

(1)

式中Nid——第i根桩的单桩竖向力设计值；

Fd——由承台底面以上的作用(或荷载)产生的竖向力组合设计值；

Mxd、Myd——由承台底面以上的作用(或荷载)绕通过桩群形心的x轴、y轴的弯矩组合设计值；

n——承台下面桩的总根数；

xi、yi——第i排桩中心至y轴、x轴的距离。

由上式可知，当公式等号后面两项均取正值即“+”时，此时桩承受的竖直力最大，即与Mxd、Myd转动方向相同一侧的桩即承台角点处的桩承受的竖直力最大，式(1)变为：

(2)

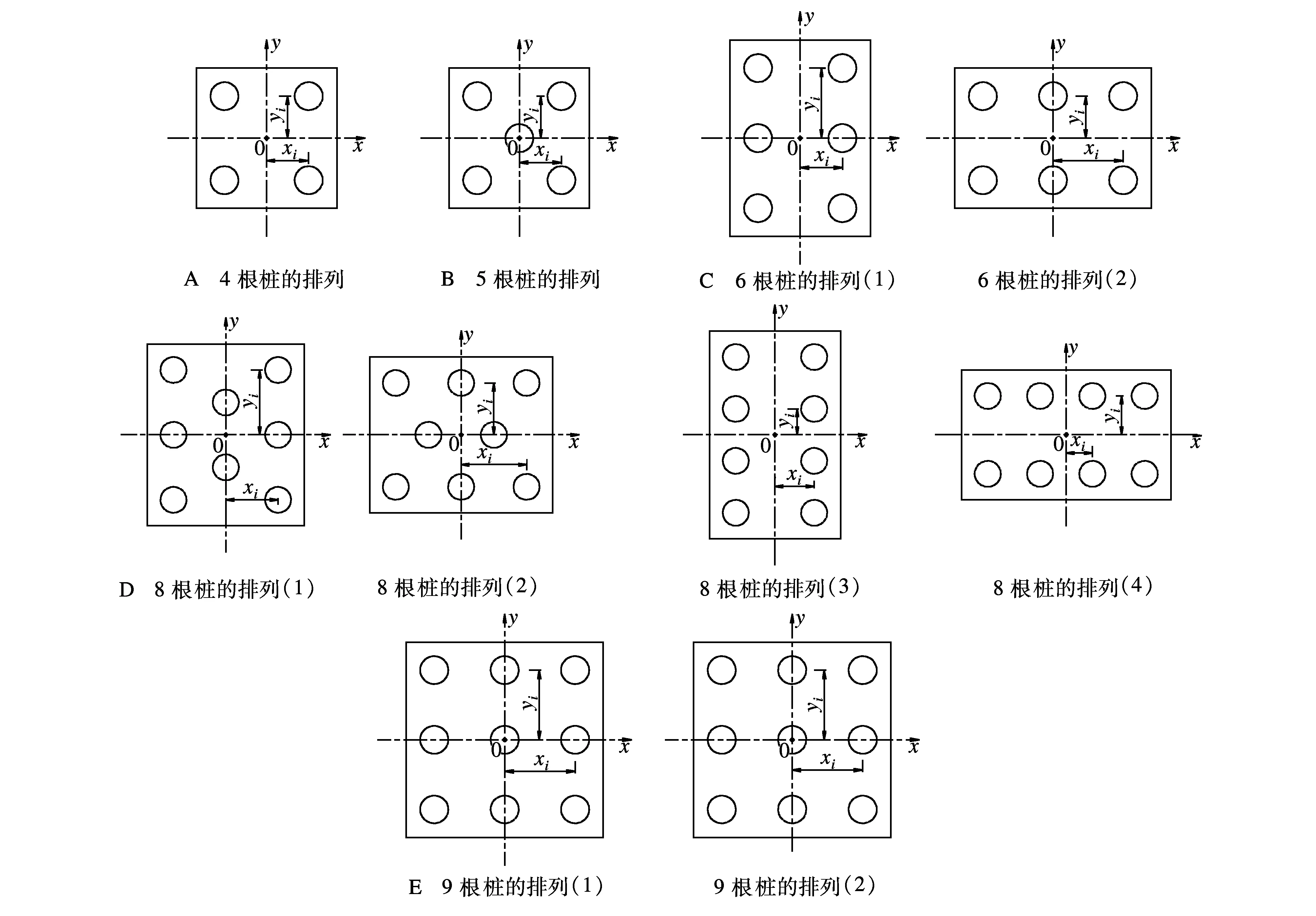
图1 群桩的排列方式(图中x轴表示纵桥向，y轴表示横桥向)

(3)

(4)

图2 承台桩基竖向力计算

研究图1中C的情况，将(1)旋转90°且将x轴、y轴互换即得到图(2)的情形，由此可知:

同理可推断图1中D(1)、(2)的情况:

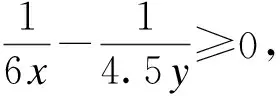
而图1中D(3)、(4)的情况:

4 示 例

某连续刚构桥，布置为63m+110m+63m，桥宽为净-6.5m+2×0.5m(防撞栏杆)，设计荷载为公路—Ⅱ级，地震动峰值加速度系数为0.15。主墩为双肢薄壁墩，高度均为25m，主墩基础为14m×10m×4m的承台加6根群桩基础。其承台加群桩基础有两种布置方式，具体布置见图3。

图3 某连续刚构桥桥型布置

该桥在初步设计时，承台及群桩基础是按图3中方式(1)布置的，该布置方式的优点是桥墩的每个墩肢纵向均对应3根桩基，桥墩传力方式明确，但承台在纵桥向似乎作用不大，仅起联系墩身及桩基的作用。考虑到按图3中方式(2)布置时，承台能很好地发挥传力作用，桩基受力更均匀，所以又按方式(2)进行了计算。

为了验证以上结论的可靠性，针对以上桥型布置，采用桥梁结构计算专用程序MidasCivil建立两个模型分别进行计算，得到在正常使用极限状态下的组合结果(见表1)。

表1 正常使用极限状态下组合结果 MPa

从表1可知，桩基按纵三横二(即图1C(2)中方式)进行排列时，各项计算值均比按纵二横三(即图1C(1)中方式)排列时的计算值略小，从而进一步验证了纵三横二的排列方式更合理。

5 结 语

(1)群桩的排列方式对桥梁整体刚度有一定的影响。由于桥梁一般纵向受力较大，群桩布置时使其纵桥向刚度较大则更合理，即群桩的排列方式在一般情况下以纵桥向多排横桥向少排受力相对更合理。

(2)在特殊情况下(如横向力风力、地震力、撞击力较大时)，为了增加桥梁横向刚度，也可将桩基按横桥向多排纵桥向少排的方式排列，此时相比桩基纵桥向多排横桥向少排的方式排列，对桥梁其它部位应力的影响并不明显。

(3)当山区某些桥梁布置桥梁承台时，若承台纵桥向长度比横桥向长度长，靠岸侧可能引起更大的边坡开挖，靠河侧可能使承台和桩基更伸入河床而增加施工难度时，也可以将承台长边布置在横桥向，短边布置在纵桥向，相应桩基也应适当调整。

参考文献：

[1] 中交公路规划设计院.JTG D62-2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》[S].北京：人民交通出版社，2004.

[2] 中交公路规划设计有限公司.JTG D63-2007《公路桥涵地基与基础设计规范》[S].北京：人民交通出版社，2007.

[3] 赵明华.桥梁桩基计算与检测[M]. 北京：人民交通出版社，2000.