直管外表面轴向半椭圆裂纹应力强度因子KⅠ的有限元分析

喻健良 闻 拓 闫兴清 伊 军

（大连理工大学化工机械学院） （大连市锅炉压力容器检验研究院)

直管外表面轴向半椭圆裂纹应力强度因子KⅠ的有限元分析

喻健良*闻 拓 闫兴清 伊 军

（大连理工大学化工机械学院） （大连市锅炉压力容器检验研究院)

利用有限元法对含外表面轴向裂纹的直管进行了分析，应用有限元软件ANSYS建立了裂纹有限元模型，采用参数化建模对内压下裂纹的应力强度因子KI进行计算，得出了影响应力强度因子的主要因素。计算表明，应力强度因子随a/t及a/c成线性变化，并与t/Do为乘幂关系。一般情况下，表面裂纹在最深点 （90°）处应力强度因子最大，然后随着角度的减小应力强度因子依次减小。但是在最浅点 （0°）处应力强度因子有回升趋势，且随着a/t的增加，这种回升趋势逐渐明显，当a/t=0.8时，甚至出现最浅点KI超过最深点KI的现象，这时对于结构的脆性起裂位置要慎重判断，不能单纯地以最深点KI为断裂依据。

应力强度因子 有限元法 表面裂纹 半椭圆裂纹 直管

0 引言

脆性断裂是高压输运管线常见的失效形式，尤其在介质泄漏时易形成低温的场合，脆断往往造成灾害性后果。因此研究管线典型缺陷型式下的力学响应及参数意义重大。应力强度因子KI是判断裂纹脆断行为的重要参数之一。对于典型裂纹的KI值，已经通过实验方法确定，并被编制成手册[1]。对于其他裂纹型式，由于实验开展不便，常借助数值方法如有限元法、有限差分法、边界元法等解决，如Jr.JC Newman及I.S.Raju采用有限元法研究直管内外壁表面裂纹[2-3]，Chai Guozhong等用边界元法[7-8]研究直管内壁表面裂纹。在这些方法中，由于有限元法简单、精确，已被证实是研究KI的有效方法。

目前，笔者在调研时发现，相当一部分直管外表面缺陷可以规则化为外表面椭圆裂纹，但目前的文献资料对外表面椭圆裂纹KI的研究较少，还没有精确的解析解，有限元解也未开展。鉴于此，本文通过有限元分析方法，对直管外壁表面椭圆裂纹进行研究，着重分析了影响裂纹KI的因素，并给出了KI的计算方法。

1 外表面椭圆裂纹有限元模型的建立

1.1 模型基本假设

为了建模方便，本文假设如下：

（1）由于直管外壁表面裂纹结构是对称的，分析时取四分之一模型计算；

（2）裂纹扩展方向为裂纹线的法线方向；

（3）裂纹面形状为半椭圆表面裂纹，深度为a，长度为2c，如图1所示；

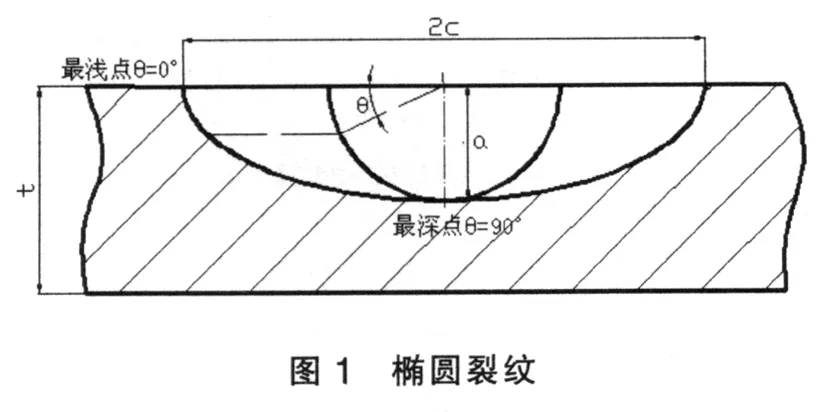
（4）KI求解角度自最浅点向最深点依次为0°～90°。

1.2 应力强度因子模拟解与理论解对比

由于裂纹前缘的应力场存在一个数学上的奇异点，为了真实反映裂纹尖端的奇异性，在裂纹前沿设立1/4节点单元。ANSYS对于计算应力强度因子提供了一种方法：位移外推法。将通过该方法得到的结果与理论解进行对比，其相对误差不大，如表1所示。

表1 平板穿透裂纹单向拉伸模型模拟与理论结果对比

1.3 模型建立

通过ANSYS自带的APDL语言进行参数化编程。为提高运算速度，仅裂尖单元采用SOLID 95单元，其余单元均采用SOLID 45单元建模。第Ⅰ类应力强度因子KI为裂纹面张开所造成，因此利用ANSYS的位移外推法时必须以裂纹扩展方向为基准。对于椭圆裂纹，其扩展方向是裂纹前缘的法线方向，这就要求在知晓椭圆方程的情况下，获得裂纹前缘已知点处的法线方程，然后据此法线方程创建已知点处的局部柱坐标系，再通过此柱坐标系创建裂尖节点。在生成节点之后还要在裂尖处构建局部卡尔坐标系，x轴指向裂纹扩展方向，y轴平行于裂纹面法线，局部卡尔坐标系是为求解应力强度因子做准备的。以上步骤完成了裂纹前缘某一个位置的裂尖节点构建，最后还需要采用整体循环得到裂纹前缘所有已知点的裂尖节点。至此，椭圆裂纹裂尖节点构造完毕。有限元模型如图2所示。

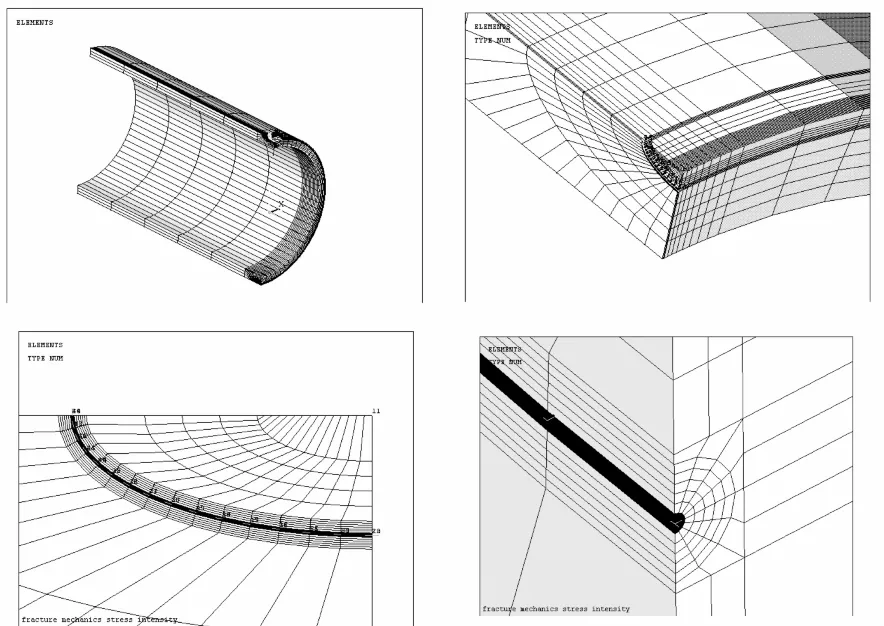
图2 有限元模型

1.4 模型计算参数及约束施加

模型几何参数如下：管道规格为DN200 mm，外径Do=219 mm，厚度t可变。p=1 MPa,根据戴维南原理，确定直管段长度L=3Do以消除端面对应力强度因子的影响，模型弹性模量E=2×105MPa,泊松比 ν=0.3。

在远离裂纹的直管端面施加z向约束，选取此截面任意一个节点施加全约束以防止直管出现刚体位移，在对称面施加对称约束。

2 计算结果及分析

对不同参数下的外表面椭圆裂纹KI值进行了计算。为叙述方便，以裂纹深度与长度比a/c、深度与厚度比a/t、厚度与外径比t/Do和角度θ为参数，讨论KI变化规律。但是，通过大量模拟数据发现，这四个参数对KI的影响是互相关联的。

2.1 KI的影响因素

2.1.1 KI随角度θ的变化规律

当 t/Do=0.1,a/t=0.2， a/c=0.2～0.8时， KI随角度θ的变化规律如图3所示。

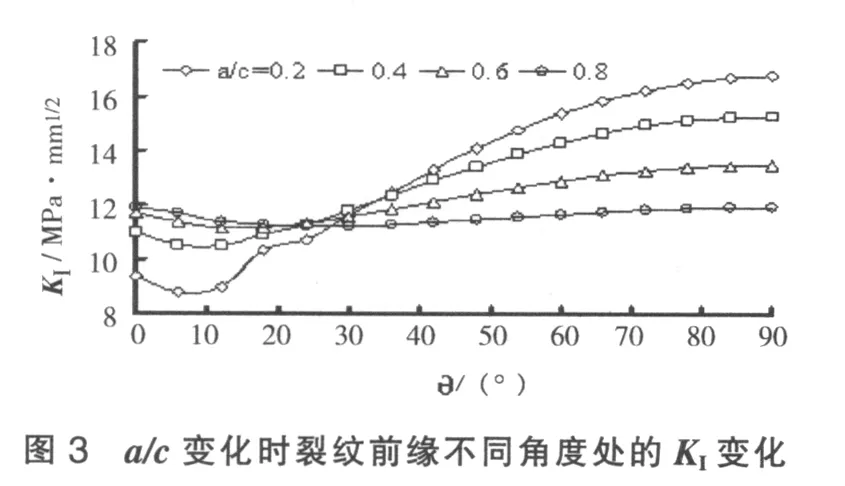
由图3可知，KI随着角度θ的增加首先有一下降过程，然后逐渐递增。其原因是直管外壁面没有刚体约束，导致最浅点 （处于外壁面）处裂纹张开位移较大，而位移外推法正是基于裂纹张开位移得出的，因此位移外推法能够直观地反映出直管外壁表面裂纹的这种特有现象。当a/c较小时，裂纹最深点KI处于主导地位，其值最大；随着a/c的增大，KI变化梯度逐渐降低，且最深点KI的主导地位逐渐丧失；当a/c=0.8时，甚至出现最浅点KI基本等于最深点KI的情况，此时最深点和最浅点两个位置具有同样的危险性。

2.1.2 KI随a/c的变化规律

当 t/Do=0.05,a/t=0.2， θ=30°、 60°、 90°时， KI随a/c的变化规律如图4所示。

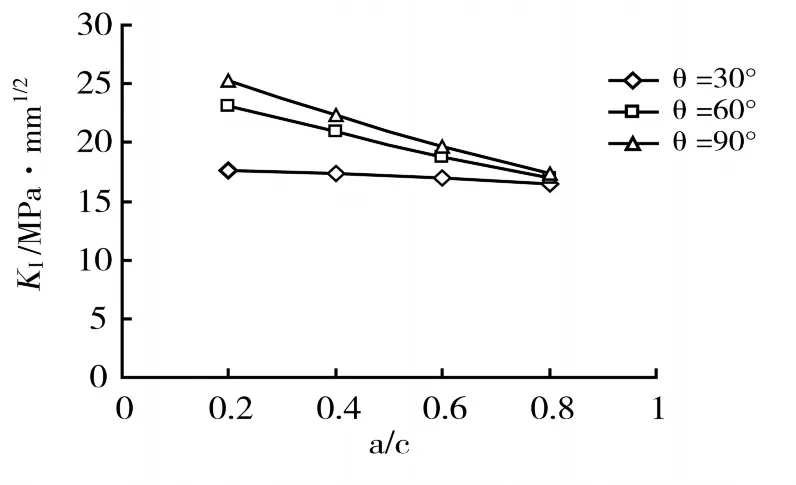
图4 KI随a/c的变化规律

由图4可知，其他参数一定时，KI与a/c呈线性关系，且随着a/c的增大，KI逐渐降低。此外，其他参数变化时，KI与a/c依然保持线性关系。

2.1.3 KI随a/t的变化规律

当 t/Do=0.05,a/c=0.4， θ=30°、 60°、90°时， KI随a/c的变化规律如图5所示。

由图5可知，其他参数一定时，KI与a/t呈线性关系，且随着a/t的增大，KI逐渐增大。此外，其他参数变化时，KI与a/t依然保持线性关系。

2.1.4 KI随t/Do的变化规律

当 a/c=0.2,a/t=0.2， θ=30°、 60°、 90°时， KI随t/Do的变化规律如图6所示。

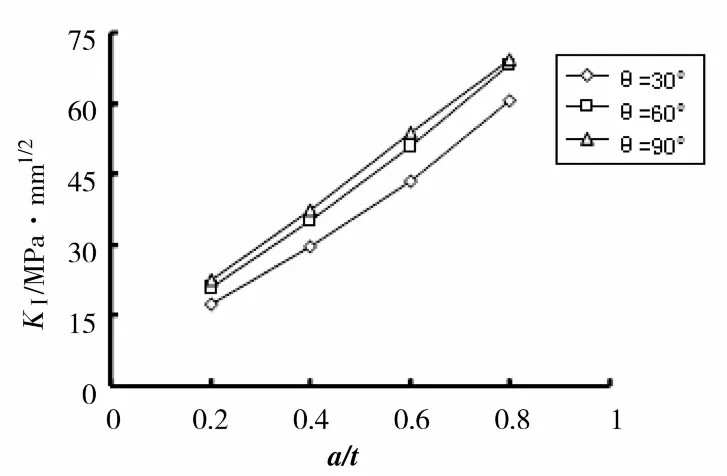
图5 KI随a/t的变化规律

图6 KI随t/Do的变化规律

由图6可知，其他参数一定时，KI与t/Do为乘幂关系，且随着t/Do的增大，KI逐渐降低。此外，其他参数变化时，KI与t/Do依然保持乘幂关系。

2.1.5 外自由壁面对KI的影响与集中点现象

不同参数下a/t对KI的影响如图7所示。

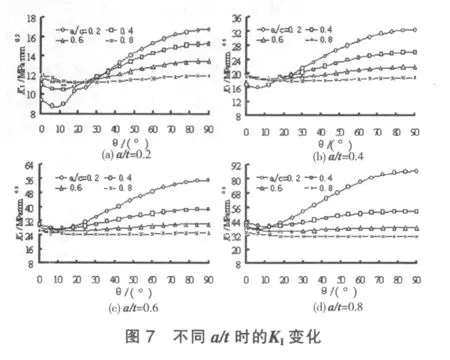
由图7可知，有两个现象：

（1）直管外壁面因刚体约束缺失所影响的KI角度范围基本在6°之内，且在此范围内，随着a/t增大，相同a/c下的相同角度位置的KI逐渐增大。a/c越大，最深点KI主导地位丧失越严重，当a/t=0.8、a/c=0.8时，甚至出现最浅点KI高于最深点KI的现象。

（2）不同a/c的曲线都通过一个公共交点，此点所对应的角度随着a/t的增加而逐渐减小，逐渐趋于发散。

3 结论

（1）在相同条件下，随着a/c的减小，应力强度因子KI变化梯度增大，且a/c越小，结构越容易发生失稳断裂。

（2）直管外壁表面裂纹KI基本维持在最深点最大，评判裂纹危险性可以以最深点KI数值为准。但是当a/c及a/t均较大 （大于0.5）时，最浅点KI也不容忽视，这时如果仅以最深点KI做评判，可能会得出错误的评判结果。

（3）计算表明，在角度为6°之后，随着角度增加，KI逐渐增大；KI与a/c为线性关系，与a/t为线性关系，与t/Do为乘幂关系。

（4）相同条件下，a/t较大且a/c较小时，结构处于最危险状态。

[1]Akram Zahoor.Ductile Fracture Handbook[M].California:Electric Power Research Institute，1989:1-3.

[2]Newman Jr JC,Raju I S.An empirical stress intensity factor equation for the surface crack[J].Engng Fracture Mech， 1981， 15： 185-192.

[3]Raju I S.Stress-intensity factors for internal and external surface cracks in cylindrical vessels[J].Journalof Pressure Vessel Technology， 1982， 104： 293-298.

[4]Calculation of stress intensity factors for a longitudinal semi-elliptical crack in a finite-length thick-walled cylinder[J].Faculty of Mechanical Engineering，2007:85-94.

[5]王永伟,林哲.表面裂纹的三维模拟及应力强度因子计算 [J].中国海洋平台,2006，21（3）：23-26.

[6]程长征,牛忠荣.边界元法计算浅表面裂纹应力强度因子[J].合肥工业大学学报，2009,32(4):503-507.

[7]Diamantoudis A Th.Stress intensity factors of semielliptical surface cracks in pressure vessels by globallocal finite element methodology[J].Engineering Fracture Mechanics， 2005， 72:1 299-1 312.

[8]Chai Guozhong.Stress intensity factors for interaction of surface crack and embedded crack in a cylindrical pressure vessel[J].International Journal of Pressure Vessels and Piping,2000,77:539-548.

Finite Element Analysis of Stress Intensity Factor for Straight Pipes’Axial Semi-elliptical External Surface Cracks

Yu Jianliang Wen Tuo Yan Xingqing Yi Jun

Straight pipes with axial semi-elliptical external surface cracks has been analysed by threedimensional finite element method.A finite element model of the cracks has been built using ANSYS,and a parametric model has been conducted to calculate the stress intensity factors(SIFs)of the semi-elliptical cracks under internal pressure,and the main factors that impact the SIFs has been obtained.Caculation shows that the SIFs changes linearly with a/t and a/c,in addition,the it’s exponentiation relationship between SIFs with t/Do.Usually,the SIFs is biggest at the deepest point(90 degree)and gradually decrease with the degree’s decrease,but the SIFs has uptrend at the shallowest point(0 degree),and the uptrend is noticeable with the increase of a/t.Even when a/t is equal to 0.8,the SIFs’ value at the shallowest point is bigger than the deepest’s,then the location of brittle crack must be judged cautiously,it’s could’t simply judged by the SIFs at the deepest point.

Stress intensity factors;Finite element method;Surface cracks;Semi-elliptical cracks;Straight pipe

TQ 050.1

*喻健良，男，1963年生，教授。大连市，116023。

2011-08-11）