GPS 弱信号的高灵敏度捕获算法

樊 静

(重庆大学通信工程学院，重庆400044)

0 引言

全球定位系统(global positioning system，GPS)是能够提供实时位置、速度和时间的卫星广播系统［1］。通常把信号强度在－188～－174 dBW之间的GPS信号视为GPS弱信号［2］。比普通的GPS信号强度－154.6 dBW低20～33 dB。对采用码分多址技术的GPS系统而言，信号捕获需要高的处理增益，一般采用延长积分时间的方法来提高处理增益;高灵敏度捕获技术即是指通过算法来提高接收机的处理增益，使其能够捕获一般接收机所不能捕获的GPS微弱信号的技术［3］。因此GPS微弱信号的捕获技术在GPS系统研究中起着至关重要的作用。缩短捕获时间和提高捕获灵敏度是研究捕获算法的关键问题。当前，常用的经典捕获算法有:相干累积［2，4］和非相干累积［2，4］捕获算法。不少学者将其相结合以进行优化，如文献［5］采用的半比特交替法以及估计导航比特位跳变的全比特方法;文献［6］以快速傅里叶变换(fast fourier transformation，FFT)为基础，采用相关累积和非相关累积对较长的信号进行处理，来提高捕获灵敏度。其本质都是相干与非相干的结合。

鉴于经典捕获算法的优缺点，本文研究一种以FFT为基础、能在低信噪比条件下可靠工作的差分相干累积算法。与传统捕获算法相比，此算法既能明显改善检测统计量的信噪比，又能缩短捕获时间。同时，采用蒙特卡罗仿真，考虑多个参数对算法性能的影响。

1 GPS信号模型及典型算法分析

1.1 GPS信号模型

GPS软件接收机进行信号处理的数据来源为射频前端的中频信号，对其以fs的采样频率进行采样得到数字中频信号，其数学模型可表示为［4］

(1)式中:tj为采样时刻;A为信号幅度且对噪声方差归一化;D为导航数据;C为C/A码(coarse/acquisition code)，码长为1 023 chip，码速率为1.023 MHz;fd为多普勒频移;τ为码时延;fIF为中频;θ0为初始相位;n为均值为零，方差为1的高斯白噪声。

接收到的数字中频信号先乘以本地复现载波，再与本地C/A码进行相关处理，即得到用于捕获的判决量，其中本地生成信号可表示为［4］

(2)式中:CL为本地PN码;τL为本地码时延;θL为本地载波初始相位;fdLl为本地载波多普勒频移。

1.2 典型捕获算法分析

GPS信号捕获是一个二维搜索过程，捕获的目的就是确认接收信号中的可见卫星，并得到相应卫星的C/A码初始码相位τ和载波多普勒频移fd的粗略估计值，然后将这些估计量送入跟踪模块，对跟踪模式进行初始化［7］。

对一般的GPS信号，通常只需处理1 ms的导航数据，就可以完成GPS信号的捕获;但对于GPS弱信号而言，处理1 ms的导航数据所得的判决变量并不可靠，难以实现捕获;此时需要对多个周期的伪码相关结果进行一定方式的累积，来提高处理增益，改善信噪比特性。典型捕获算法有:相干累积和非相干累积算法。

1.2.1 相干累积算法

相干累积是将不同周期的接收信号与本地信号的相关值进行对应累加。以得到判决变量，其数学原理为［8］

(3)式中:Yk(τ，fd)为第k个C/A码周期的相关值矩阵;τ为码相位点;N为相干累积次数。

相干累积算法可以显著提高信噪比。但受导航数据位翻转的影响，相干累积时间一般不得超过20 ms，且相干累积的结果乘有系数因子，其中T为相干累积时间。为了避免相关值的衰减，且缩短捕获时间，相干累积时间T不能太长［9］。

1.2.2 非相干累积算法

非相干累加是对相关结果取模的平方，再进行第二次累加的过程，进一步提高信噪比，以得到判决变量，其数学原理为［10］

(4)式中，Yk(τ，fd)为第k个相干累积矩阵的结果。

由于此法是在相干累积基础上进行第二次累积，所以相干累积的时间不必设得很长，这样频率搜索步长便可设得大一些，缩短捕获时间。但是，此法会引入“平方损失(squaring loss)”［3］，因为在非相干累积中，噪声和信号同时被平方，使信噪比的改善效果降低。非相干累积对信噪比的提高没有相干累积效果好;若想得到满意的信噪比，需要增加非相干累积次数。

第一，不明确给予其定位。《广东省农村集体经济组织管理规定》第十八条第一款规定，县级人民政府或者不设区的市人民政府免费向农村集体经济组织颁发组织证明书，具体工作由农业行政主管部门负责。虽然给予颁发证书，但是不明确定位其主体地位，该规定回避了这个问题。

2 差分相干累积捕获过程

差分相干累积通过抑制随机及伪随机噪声，能够很好地应用于有相对较高噪声或干扰的系统中。在文献［10－11］中对差分相干法的检测变量所服从的分布进行了数学推导。基于此，并综合对相干累积及非相干累积的分析，将差分相干累积算法应用于GPS微弱信号的高灵敏度捕获中。

差分相干累积捕获算法的基本思想是:首先进行相干累积，然后将相邻的相干累积结果进行共轭相乘再累加。图1为基于FFT的差分相干算法的原理图。其数学原理为

(5)式中，Y*k－1(τ，fd)为 Yk－1(τ，fd)的复共轭。由(5)式可知，不同于非相干累积中同一样点噪声的自乘，差分相干累积是将相邻样点的噪声共轭相乘。其噪声为高斯白噪声，由于高斯白噪声在任意2个不同时刻的采样信号是统计独立的，所以前后相邻样点噪声相乘累加的结果理论上均值应该为0，对噪声的放大相对较小;且根据C/A码的循环平稳特性，相邻样点的信号相关累加结果具有高度的相关性，因此，差分相干累积法对信噪比的改善效果优于非相干累积，减小了非相干累积带来的平方损失影响。

该算法的具体步骤如下。

步骤1 将所得数字中频信号乘以本地载波信号之后再进行FFT处理。其中I，Q两支路分别作为FFT的实部和虚部进行复数FFT运算。

步骤2 对本地伪码信号进行FFT运算，并取其复共轭。

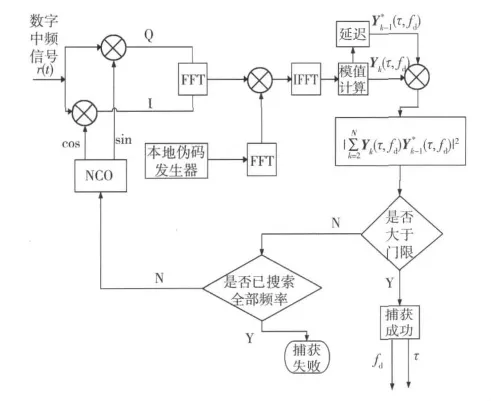
图1 基于FFT的差分相干算法原理图Fig.1 Structure of differential coherent integration based on FFT

步骤3 将步骤1所得结果与步骤2所得结果进行相乘。

步骤4 对步骤3所得的相乘结果进行快速傅里叶反变换(inverse fast fourier transformation，IFFT)运算，并取模值;这样便可得到所有码相位单元的相关值，即实现在估计的多普勒频点一次性搜索所有的伪码相位，通过FFT运算，大大缩短了捕获时间。其中码相位搜索范围为1 023码片、多普勒频移搜索范围为±10 kHz。然后进行差分相干累积，将前后相邻周期的相干累积矩阵的结果进行共轭相乘再累积，将所得检测变量进行门限判断，若所有码相位单元上的检测变量值都比预设门限小，则调整本地载波数控振荡器(number control oscillator，NCO)，使多普勒频移步进一单元，继续进行搜索，若所有频率单元搜索完毕，检测变量值仍然比门限小，表明期望的卫星信号不存在，此次操作结束，转而捕获其他卫星的信号;若某码相位单元上的检测变量值大于预设门限，表示信号捕获成功，其最大值对应的第i个频率与第n个位置分别对应C/A码的载波频率和起始位置。

综上所述，差分相干累积算法中的相干累积时间不用设得很长，即频率搜索步长不用设得太小，从而缩短捕获时间。也减小了非相干累积算法带来的“平方损失”，同时能够提高灵敏度、改善信噪比增益。

3 算法性能仿真分析

根据上文所述，本文以FFT为基础，采用差分相干累积算法，延长累积时间。由(4)—(5)式可知，非相干累积和差分相干累积都是在相干累积结果上进行的二次累积，所以捕获性能肯定优于相干累积，故本文对在相干累积基础上进行的差分相干累积和非相干累积法进行大量的仿真，比较其在不同累积次数及不同载噪比(carrier to noise ratio，C/N0)情况下的捕获概率。

仿真环境为MATLAB，采用仿真GPS数据，系统采样率为5 MHz，未考虑多普勒效应的中心频率是1.25 MHz。每个载噪比下执行蒙特卡罗仿真1 000次。图2和图3分别表示取相干累积时间为1 ms和5 ms情况下，差分相干累积与非相干累积的捕获概率与载噪比的关系性能比较。其中差分相干的累积次数用DFC表示，非相干的累积次数用NCH表示。

从图2和图3可以得出以下结论。

1)由图2可见，当累加次数较大时，在相同的捕获概率下，差分相干优于非相干约1.8 dB。DFC=19时，差分相干的性能几乎与NCH=30时的非相干性能相当，DFC=29时，差分相干的性能甚至超过了NCH=40时非相干的性能，这充分说明了差分相干在高灵敏度捕获中的优势。

2)由图2可见，在相同的捕获概率下，NCH=30相对于NCH=20，非相干算法性能提高了约1.5 dB，而DFC=29相对于DFC=19，差分相干算法性能提高了约1.8 dB;NCH=40相对于NCH=30，非相干算法性能提高了约0.8 dB，DFC=39相对于DFC=29，差分相干算法性能提高了约1 dB。这说明随着累加次数的增大，2种算法的捕获性能提高率虽然都会有所下降，但差分相干累积的性能提高率始终大于非相干累积的性能提高率。

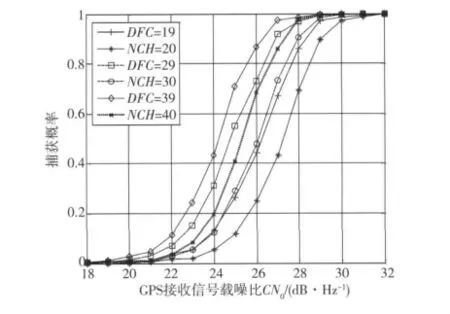
图2 1 ms相干累积时差分相干与非相干的性能比较Fig.2 Comparison of the Performance between the differential coherent integration method and the non－coherent integration method based on a coherent integration over 1 ms

3)由图3可见，随着相干累积时间的增加，差分相干累积和非相干累积的性能都得到了提高，但是在同样载噪比及相同累积次数的条件下，差分相干累积的捕获概率始终大于非相干累积的捕获概率，这也充分表明了差分相干在捕获弱信号方面的优势。

图3 5 ms相干累积时差分相干与非相干的性能比较Fig.3 Comparison of the Performance between the differential coherent integration method and the non－coherent integration method based on a coherent integration over 5 ms

4 总结

本文鉴于传统方法对GPS微弱信号捕获的不足，研究一种以FFT为基础，基于相干结果共轭乘累加的差分相干累积算法，分析了载噪比、累加次数、相干累积时间的选取对差分相干累积算法性能的影响。通过MATLAB仿真实验表明，差分相干累积算法很好地解决了传统算法中遇到的导航数据位比特翻转以及平方损失的问题，并能确保较短的捕获时间。在无需增加硬件复杂度的条件下，该方法捕获GPS弱信号的灵敏度明显优于传统的弱信号捕获技术，促进了GPS软件接收机的发展应用。

［1］CHEN Ying－mei，LI Zhi－qun，WANG Zhi－gong，et al.Design of an L1 band low noise single－chip GPS receiver in 0.18 μm CMOS technology［J］.The Journal of China Universities of Posts and Telecommunications，2010，17(3).60－65.

［2］YEN Tsui James Bao.GPS软件接收机基础［M］.2版.陈军，潘高峰，译.北京:电子工业出版社，2007:192－200.YEN Tsui James Bao.Fundamentals of Global Positioning System Receivers A Software Approach［M］.2nd ed.CHEN Jun，PAN Gao－feng，translation.BeiJing:electronics industry press，2007:192－200.

［3］WU Ling－juan，LU Wei－jun，YU Dun－shan.Research of weak signal acquisition algorithms for high sensitivity GPS receivers［C］//IEEE.PrimeAsia 2009.Asia Pacific Conference on Postgraduate Research in Microelectronics＆ Electronics.Piscataway，NJ:IEEE Press，2009:173－176.

［4］韩帅.导航接收机在弱信号下C/A码捕获技术研究［D］.哈尔滨.哈尔滨工业大学，2007.HAN Shuai.Research on the Acquisition of C/A Code in Weak Signals［D］.Harbin:Harbin Institute of Technology，2007.

［5］PSIAKI M L.Block acquisition of weak GPS signals in a software receiver［J］.Proceedings of the ION GPS，2001:2838－2850.

［6］胡丛玮，李晓玲，安雷.一种改进的GPS微弱信号捕获方法［J］.武汉大学学报:信息科学版，2008，33(8):821－823.HU Cong－wei，LI Xiao－ling，AN Lei.AN Improved Algorithm for Acquisition of Weak Signal in a Software GPS Receiver［J］.Geomatics and Information and Information Science of Wuhan University，2008，33(8):821－823.

［7］王金刚.GPS数字中频信号仿真及捕获验证［J］.重庆邮电大学学报:自然科学版，2010，22(2):253－257.WANG Jin－gang.Simulation and acquisition valid－ation of digital IF GPS signals［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2010，22(2):253－257.

［8］梁坤，施浒立.高灵敏度GPS捕获技术的分析与仿真［J］.全球定位系统，2007，(6):26－32.LIANG Kun，SHI Hu－li.Analysis and Simulation of High Sensitivity GPS Acquisition Techniques［J］.GNSS World of China，2007，(6):26－32.

［9］蔡昌听，皮亦鸣.高灵敏度GPS技术的研究进展［J］.全球定位系统，2006，(2):1－9.CAI Chang－ting，PI Yi－ming.Progress in High－Sensitivity GPS Techniques［J］.GNSS World of China，2006，(2):1－9.

［10］AVILA Rodriguez J A，Heiries V，Pany T，et al.Theory on acquisition algorithms for indoor positioning［C］//IEEE.Proceedings of 12th Saint Petersburg International Conference on Integrated Navigation Systems.Piscataway，NJ:IEEE Press，2005:23－25.

［11］WEI Yu.Performance evaluation of a differential approach based detector［C］//Proceedings of the Institute of Navigation－19th International Technical Meeting of the Satellite Division，ION GNSS 2006Fort Worth，TX，U－nited states:Institute of Navigation，2006:2441－2452.