基于改进型神经网络的电能质量扰动识别

金燕，钟金金，章旌红

(浙江工业大学 信息工程学院，浙江 杭州 310023)

0 引言

敏感性电子设备如计算机、微电子控制器、变速驱动器的广泛使用，电力工业及其用户对电力系统的电能质量要求日益严格。同时，由于不对称、非线性、波动性负荷在容量和数量上的大量增加，电能质量的污染日趋严重[1]。因此，准确识别扰动信号对电能质量的分析非常重要，也是电能质量问题进行治理和改善的前提条件。

近年来，基于神经网络的电能质量识别方案获得了一定效果。电能质量识别系统中，特征向量提取方法主要包括 Fourier变换[2]、dq 变换[3]、S 变换[4]及小波变换[5]等，识别方法有:人工神经网络[5]、模糊逻辑[6]、专家系统[7]及支持向量机[4]等。其中支持向量机训练时间短，实时性能好，但对大规模训练样本难以实施，提高训练样本后，分类效果明显下降。传统神经网络的算法收敛性差，训练时间长，泛化能力不足且难以保证精确度和速度的要求。

为弥补传统方法的不足，一些学者提出了遗传算法优化的BP神经网络[8]，利用遗传算法的并行性和全局搜索能力克服了传统BP神经网络容易陷入局部最小的缺点，但优化后的神经网络仍易出现过拟合现象且网络节点数偏多。因此，本研究中将遗传算法和贝叶斯正则化神经网络相结合，增强网络泛化能力。仿真结果表明，此方法训练时间短，收敛性好，不易出现过拟合现象且对多数扰动信号类型均适合。

1 扰动信号特征向量的提取

1.1 小波包分解原理

小波包变换是小波变换的完善和发展，它对小波变换中没有分解的高频部分也进行了细分，且小波包变换可以自适应选择频带，提高了处理信号的能力，更适合用于非平稳信号的分析。

序列{wn(t)}称为由基函数wn(t)=φ(t)确定的小波包。且(1)式中g(k)=(－1)kh(1－k)，g(k)和h(k)分别是相互正交的低通滤波器与高通滤波器的系数。

1.2 小波包能量熵

原始信号S(t)的j层小波包分解序列为Sj，其中(k=0，1，2，…，2j－1)。定义原始信号在k个尺度上的能谱Ei为:

式(2)中，Dk(i)为单支重构后所得信号分量。

信号总能量E等于各点能量Ei(i=1，2，…，k)之和，即:设 Pj，k(i)=Ei/E，则∑kPj，k(i)=1，其中 Pj，k(i)反映了小波包能量在各个频带的分布情况。Shannon能量熵是对信息源的平均信息量的衡量，是对系统状态不确定程度的一种度量[9]。将小波包与能量熵结合在一起，定义小波包能量熵为:

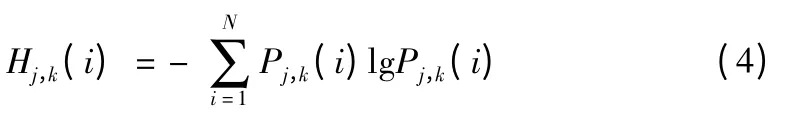
式(4)中N为原始信号的长度。

2 改进型神经网络

2.1 BP 神经网络

近年来，神经网络在模式识别和故障诊断中得到广泛应用，其中BP神经网络是应用最广泛的。BP神经网络是一种多层前向神经网络，其主要特点是信号前向传递，误差反向传播，一般由输入层、隐含层和输出层组成。传统BP神经网络训练速度太慢、易陷入局部最小，且其结构参数的设置复杂，很难满足工程实践的需要[10]，为了克服传统 BP神经网络的不足，一些学者提出了采用遗传算法对其进行优化。

2.2 遗传算法优化BP神经网络

遗传算法(GA)是美国Michigan大学Holland教授1962年提出的，已广泛应用于许多领域。它是建立在自然选择及群体遗传学机理基础上的一种搜索法[11]，将生物的进化过程描述为选择、交叉、变异3个算子，是问题求解和最优化的有效工具。

基于遗传算法优化的BP神经网络主要是指在BP神经网络的学习过程中，引入遗传算法进行迭代，直到收敛。此算法有较强的收敛性和有效性，但优化后的神经网络仍易出现过拟合现象，且网络节点数偏多。

2.3 遗传算法优化贝叶斯正则化神经网络

本研究中将遗传算法和贝叶斯正则化神经网络相结合，克服了传统BP神经网络易陷入局部最小，遗传算法优化后仍易出现过拟合现象且网络节点数偏多等缺点。

贝叶斯正则化方法，对标准BP神经网络算法进行改进，可利用贝叶斯的统计方法自动确定正则化参数[12]，简化参数设置的过程，提高训练速度。且贝叶斯正则化技术 能够较好的提高神经网络的泛化能力，限制过拟合现象。

标准BP算法中，采用均方误差ED作为训练性能函数:

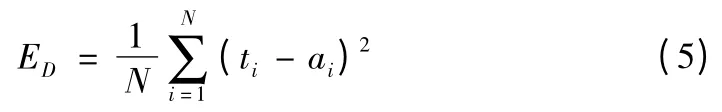
式(5)中，ti是N个训练样本中第 i个目标值，ai是第 i个输出值。正则化方法中，经改进后的网络训练性能函数如下:

其中，Ew为网络权重平方和的平均值为神经网络连接权的个数。

本文提出的遗传算法优化贝叶斯正则化神经网络的流程图如图1所示。

3 实验仿真

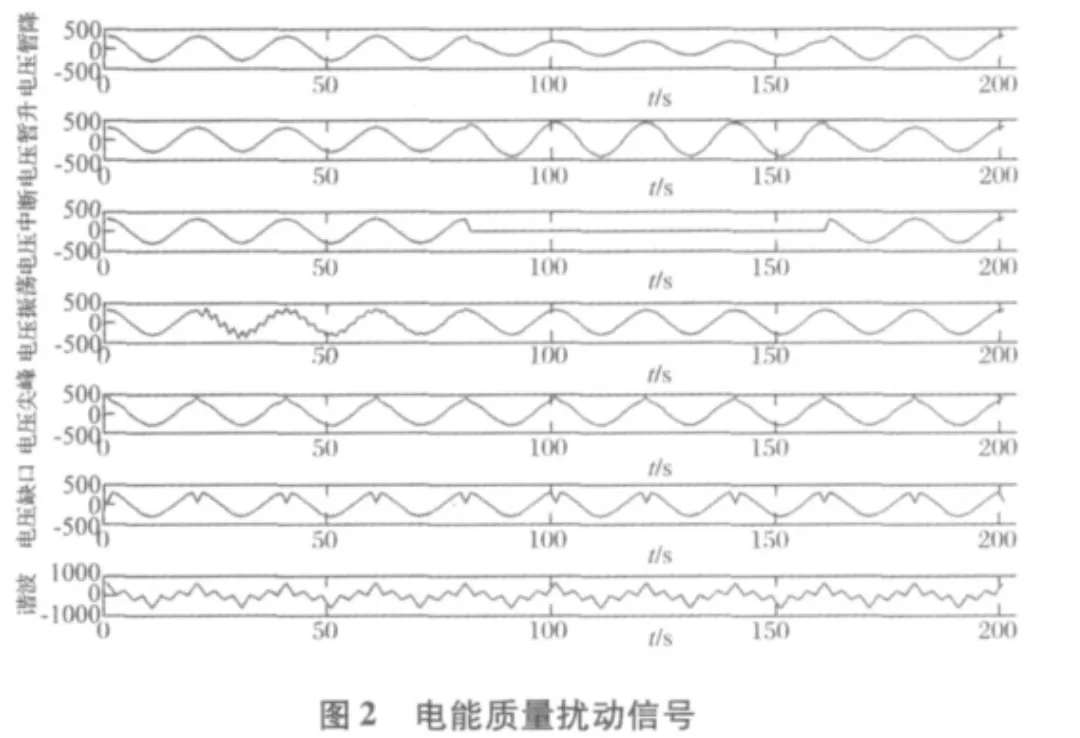
电能质量扰动信号主要包括:电压暂降、暂升，中断，振荡，电压尖峰、电压缺口和谐波等。用MATLAB软件，模拟生成上述7种测试样本，其波形如图2所示。

利用db4小波对上述7种电能质量扰动信号进行小波包变换，采用公式(4)计算其小波包能量熵，得到分布直方图如图3所示。

从图3可以看出，不同类型的扰动信号计算所得小波包能量熵分布不同，且前两个频段的小波包能量熵区别明显。因此，可以作为扰动信号识别的判据。

图1 遗传算法优化贝叶斯正则化神经网络流程

通过改变扰动信号的起始相位角、持续时间和幅值，并添加30 db的噪声，利用MATLAB产生每种信号各200个，其中训练样本60个，测试样本140个。分别采用传统BP神经网络，遗传算法优化BP神经网络，遗传算法优化贝叶斯正则化神经网络进行电能质量扰动识别测试，测试结果如表1所示。

由表1可知，遗传算法优化贝叶斯正则化神经网络的扰动识别正确率最高，且仿真过程中，该改进型神经网络稳定性好，明显优于其它两种方法。

为测试遗传算法优化贝叶斯正则化神经网络对不同噪声下的电能质量扰动信号识别的适应性，本研究针对多种信噪比情况做了仿真分析，分别取信噪比为 50 db，40 db，20 db，10 db，5 db。仿真结果显示，该改进型神经网络在环境噪声较低时，总准确率可达到99%，当噪声干扰严重时(信噪比为50 db)，准确率有所下降，但仍能保持在93%以上，且在各种噪声下的分类效果都明显优于传统BP神经网络及遗传算法优化BP神经网络。

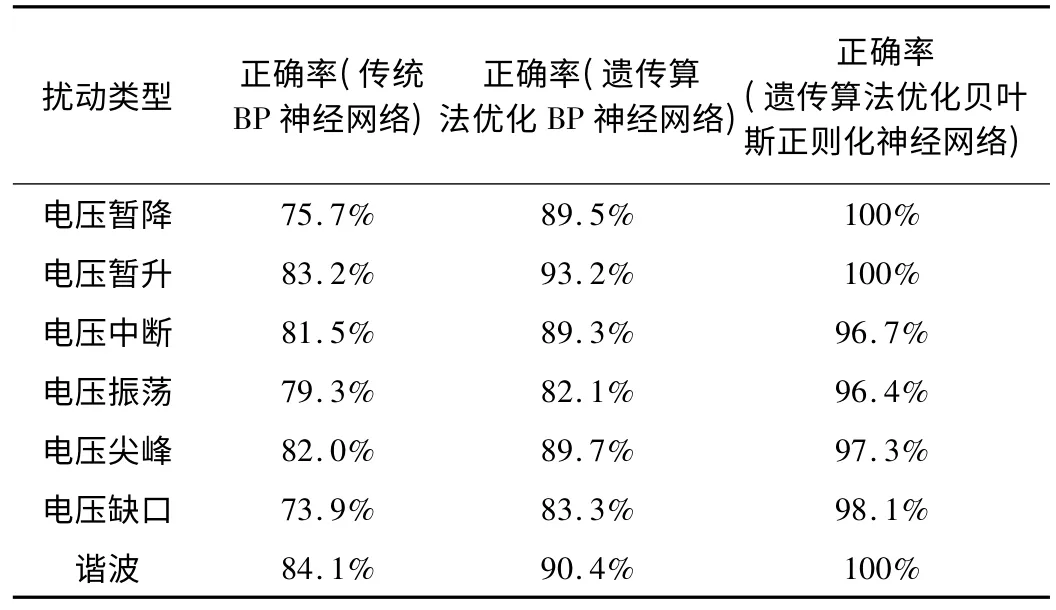
表1 不同方法对电能质量扰动识别的正确率对比

4 结束语

本研究中将遗传算法和贝叶斯正则化神经网络相结合，较好的改善了传统BP神经网络易陷入局部最小，经遗传算法优化后仍易出现过拟合现象且网络节点数偏多的缺点。改进后的神经网络应用于电能质量扰动识别，可显著提高扰动识别正确率，是一种非常有效的方法。

[1]Marques C A G，Ferreira D D，Freitas L R，et al.Improved disturbance detection technique for power － quality analysis[J].IEEE transaction on Power Delivery，2011，26(2):1286－1287.

[2]Wright P S.Short－time Fourier transforms and Wigner－Ville distributions applied to the calibration of power frequency harmonic analyzers[J].IEEE Transaction on Instrumentation and Measurement，1999，48(2):475－478.

[3]徐永海，肖湘宁，杨以涵，等.基于dq变换和ANN的电能质量扰动辨识[J].电力系统自动化，2001，25(14):24－28.

[4]占勇，程浩忠，丁屹峰，等.基于S变换的电能质量扰动支持向量机分类识别[J].中国电机工程学报，2005，25(4):51－56.

[5]Kanitpanyacharoean W，Premrudeepreechacham S.Power Quality Problem Classification Using Wavelet Transformation and Artificial Neural Networks[J].IEEE Power System Conference and Exposition，2004，3:1496－1501.

[6]周翔.基于模糊逻辑控制的SRD仿真实现[J].电气自动化，2011，33(2):67－72.

[7]Reaz M B I，Choong F，Sulaiman M S，et al.Expert System for Power Quality Disturbance Classifier[J].IEEE Transaction on Power Delivery，2007，22(3):1979－1987.

[8]岑文辉，雷友坤，谢恒.应用人工神经网与遗传算法进行短期负荷预测[J].电力系统自动化，1997，21(3):29－32.

[9]Hu GS，Zhu FF，Ren Z.Power quality disturbance identification using wavelet packet energy entropy and weighted support vector machines[J].Expert Systems With Applications，2008，35(2):143 －179.

[10]Hagan M T，Demuth H B，Beale M H.Neural network design[M].Beijing:China Machine Press，2002:35 －38.

[11]潘翀，陈伟根，云玉新，等.基于遗传算法进化小波神经网络的电力变压器故障诊断[J].电力系统自动化，2007，31(13):88－92.

[12]Gencay R，Min Qi.Pricing and hedging derivative securities with neural network:Bayesian regularization，early stopping and bagging[J].IEEE Transaction on Neural Network，2001，12(4):726－734.