中频轴承感应加热中基于频率的加热效率分析

刘二喜，赵继敏

(上海交通大学 电子信息与电气工程学院 电气工程系，上海 200240)

0 引言

分析了影响功率因数的几个主要因素，又从加热频率入手，重点研究加热频率对加热效率的影响并进行仿真，结果可以看出实现谐振频率自动跟踪控制在感应加热中应用发展的重要性和必然性，也对谐振频率自动跟踪控制有借鉴作用。

1 中频加热原理

感应加热是利用电磁感应的方法使被加热的材料的内部产生涡流，并依靠这些涡流产生的能量达到加热物体的目的[1]。感应加热的过程其实就是电磁感应过程与热传导过程的综合，而其中电磁感应过程具有主导作用，其影响在一定程度上决定着热传导过程。感应加热所遵循的主要理论依据是电磁感应、集肤效应和热传导三项基本原理[2]。

本文重点研究电磁感应过程。任何导体通过电流时，都会在其周围产生磁场。当导体中通入交变电流时，便会产生交变磁场。感应加热时，被加热的工件就切割着感应线圈产生的交变磁场。由电磁场理论可知，切割交变磁场产生的感应电动势e可用法拉第电磁感应定律表示:

感应电动势在工件的表面薄层内便形成电流，通常称这种电流为涡流。涡流强度if取决于感应电动势e和涡流回路的阻抗z。根据欧姆定律可得:

通常z非常小，所以 if能达到很高数值，使涡流回路产生大量的热[3]:

式中，R为工件电阻。

工件的加热主要就是靠这种热量。

2 负载等效电路

中频感应加热器的负载都是由电感和被加热工件组成。本实验的负载选用铁芯电感和轴承，等效为一个 n:1(n较大，本文取 n=300)的变压器。因电感很大，所以功率因素很低，通常需要串联一个电容来进行功率补偿，以提高功率因数。其等效原理图如图1。

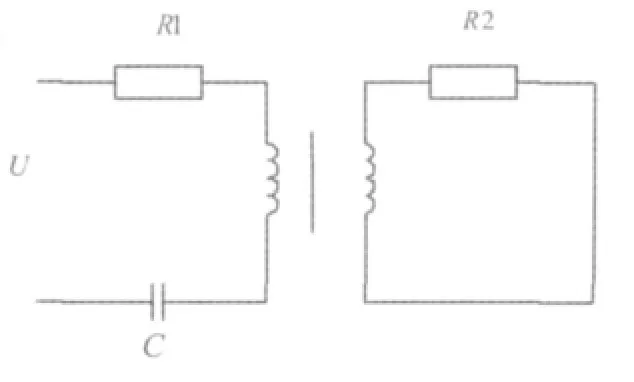
图1 加热器等效电路

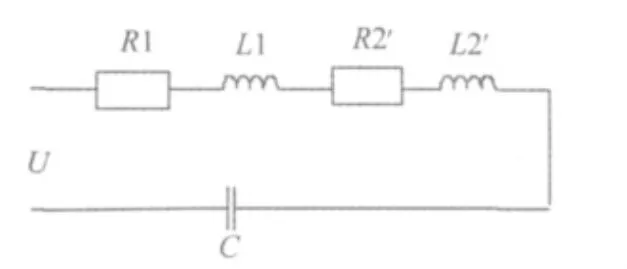
图2 简化等效电路

根据变压器的等效电路，可简化如图 2[4]。

其中 R2'、L2'分 别为R2、L2折算到原边的折合量。将R2、R2'合并为 R，L2、L2'合并为 L，进一步简化电路如图3。

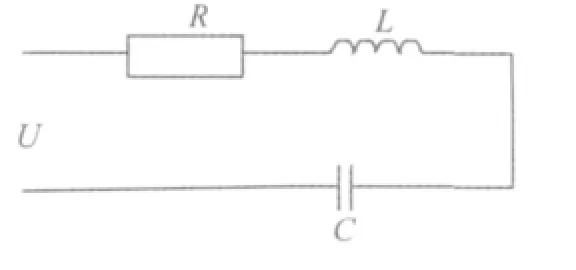
图3 最简等效电路

3 影响加热效率的

中频感应加热器连同负载组成一个电气系统，此系统可以看成由一个大电感、一个小电容和一个电阻组成的RLC回路，当电源频率与系统谐振频率一致时，电压、电流相位相同，功率因数达到最大。中频轴承感应加热器谐振频率如下[5]:

其中f0为系统谐振频率(Hz)、L为线圈与轴承组成的系统的 电感(H)、C为补偿电容(F)。

显然，当电路谐振时，电感、电容上能量相互转换，电源能量几乎全都被负载吸收并转化为内能，此时电源功率因数最高，加热效率最大。因此影响加热效率的因素就转化为使电路谐振的因素。而影响电路谐振的因素有三:电感，电容和电源频率。

电感是随轴承的不同而改变，是导致系统谐振频率改变的根本因素。电容的改变是离散的几个点，很难控制实现谐振。所以最理想的方法就是改变电源频率，使电源频率自动跟踪改变着的谐振频率，实现整个系统始终处于谐振状态或谐振状态附近。

当负载改变时，系统中谐振频率也要随着改变，就是要求电源频率不断地改变并向着已改变的谐振频率靠拢，这样就使得分析变得相当复杂。考虑到整个过程都是在重复着同样的过程:负载改变，谐振频率随之改变，电源频率向谐振频率调整。所以从中选取一个过程来分析，一旦负载给定，谐振频率就确定下来，这样既能满足分析结果的有效性，又使得分析过程大为简化。

电源频率不断地向谐振频率靠拢，功率因数也就随着上升。当电源频率满足功率因数的要求时，因为加在电阻上的电压和电流大小也要发生变化，还不一定能保证有足够的有用加热功率，因此还应该考虑到电源的有效利用率η，即实际加热功率P与谐振条件下最大加热功率Pmax之比。下面分析一下电源有效利用率η与电源频率接近谐振频率程度之间的关系:

RLC串联谐振电路的电流有效值为[5]:

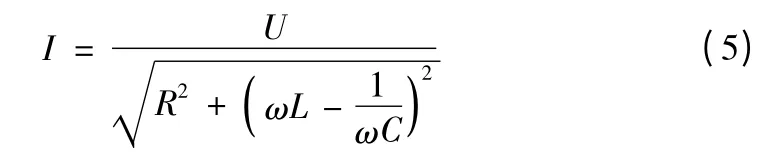
电源有用功率即消耗在电阻上的功率为:

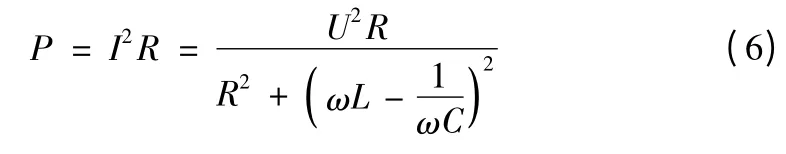
而当电路谐振时，电源的功率最大，其值为:

所以，电源有效利用效率为:

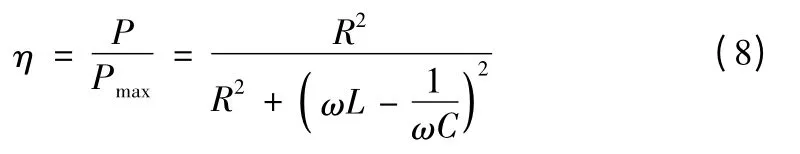
为了更清楚地表示出η与ω偏离固有频率ω0程度的关系，令 ω =nω0，则式(8)变为:

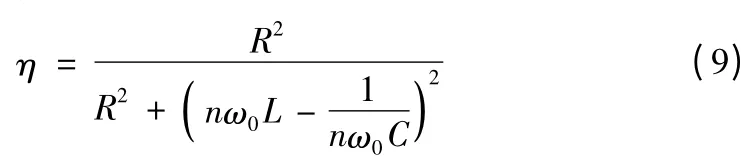
本文选取实验室中实际参数:补偿电容为18.8 nF，线圈长度33.2 cm，直径 2.2 cm，300匝的单层铁芯线圈，经测量计算，线圈电阻 0.3 Ω，其电感量为[3]:

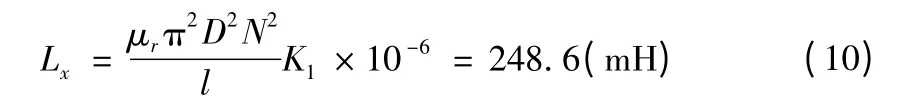
其中，D是线圈中径，取 2.2 cm;N是匝数，取300匝;l是线圈长度，取 33.2 cm;K1是修正系数，取 0.98;μr为铁芯相对磁导率，取2 000。轴承相当于单匝，折算到原边电感也为248.6 mH。

因负载运行时漏电感仅占总电感的3%以下，为计算方便，本文选取1%。因此原边漏电感和轴承折算漏电感均为2.486 mH，合计 4.972 mH。

轴承折算电阻约为50 Ω，根据(4)式得谐振频率为f0=16.46 kHz，ω0=1.034 ×105rad/s

取 L=4.972 mH，C=18.8 nF，ω0=1.034 × 105rad/s，R=50 Ω(线圈电阻0.3 Ω可忽略不计)。

以η为纵坐标，n为横坐标，对(9)式用 MATLAB如图 4所示。

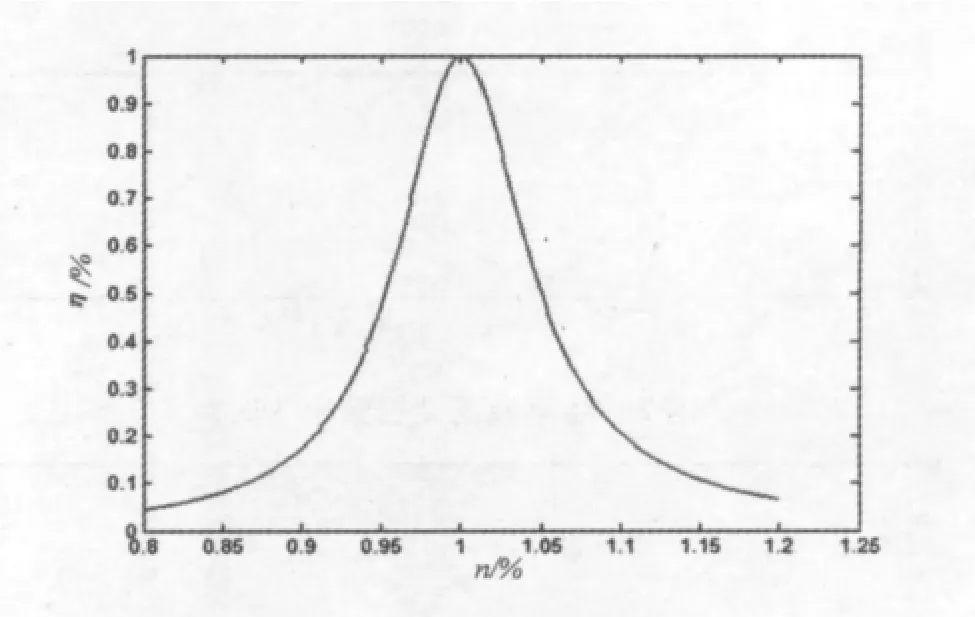
图4 η与n的关系图

由图4可见，当电源频率偏离谐振频率10%以上，电源有效利用率不到20%，要想电源有效利用率达85%以上，电源频率偏离谐振频率要在2%以内。

4 系统仿真

本仿真选用参数同上面实验系统。取 L=4.972 mH，C=18.8 nF，R=50 Ω，U=100 V，f0=16.46 kHz建立仿真模型。

图5～图9分别是电源频率在谐振频率、偏高谐振频率1%、3%、5%、10%的仿真波形图。

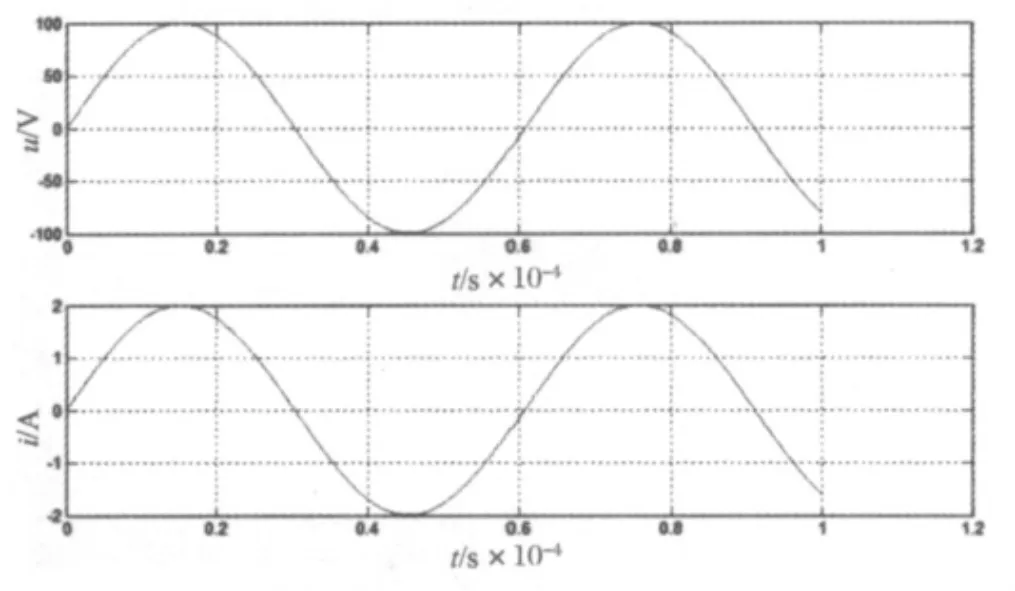
图5 频率为谐振频率

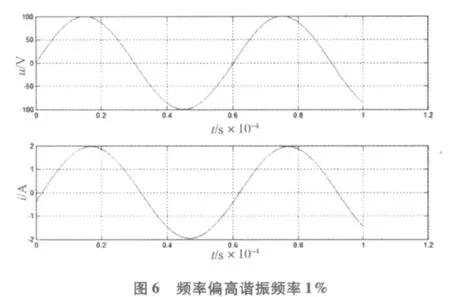
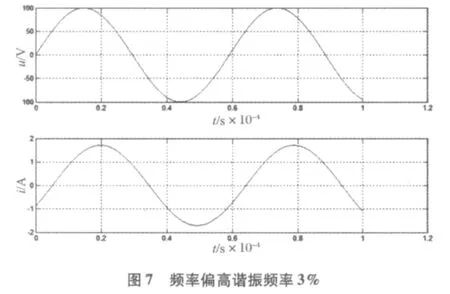
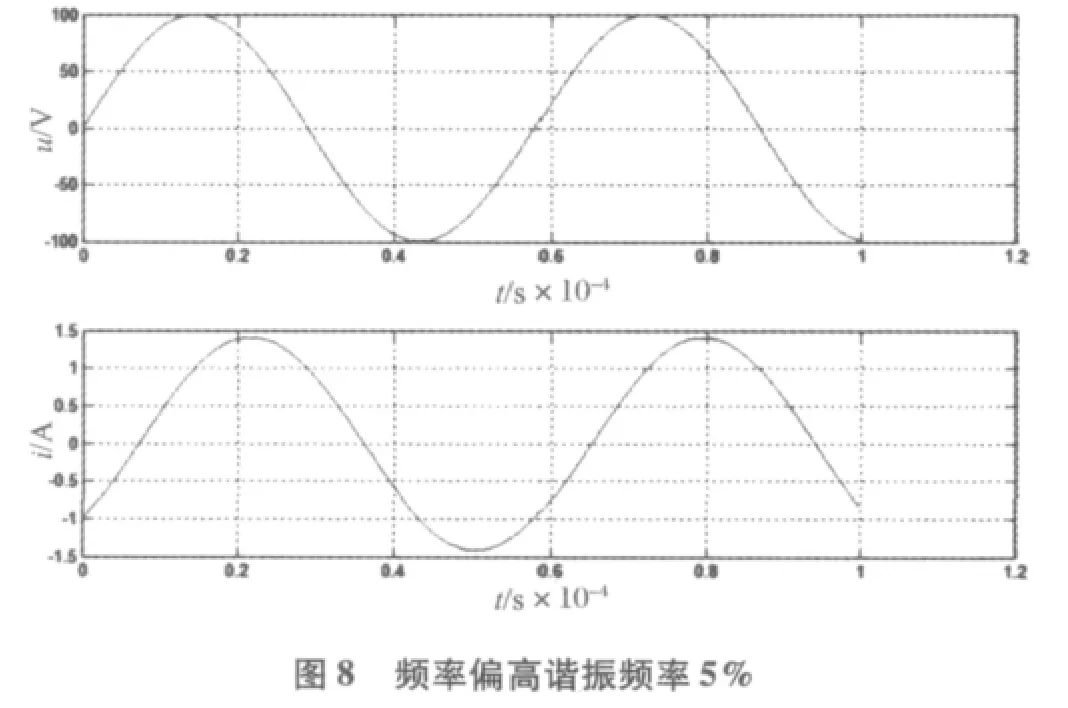
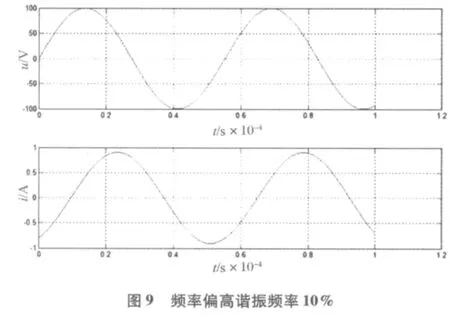
由仿真图可以读出电压与电流相位上的时间差，进而计算出相位差和功率因数;根据仿真图的电压、电流峰值也可算出有用功率和电源有效利用率。

经计算，当频率偏高谐振点1%时，功率因数0.978，电源有效利用率0.96;当频率偏高谐振点3%时，功率因数已经降到0.856，电源有效利用率0.734;当频率偏高谐振点5%时，功率因数0.71，电源有效利用率0.50;当频率偏高谐振点10%时，功率因数已经降到0.45，而电源有效利用率更是降到了0.20。

当电源频率偏低时，也做同样的仿真和计算可得:当频率偏低谐振点1%时，功率因数0.979，电源有效利用率0.959;当频率偏低谐振点3%时，功率因数已经降到0.846，电源有效利用率0.718;当频率偏低谐振点5%时，功率因数0.686，电源有效利用率0.471;当频率偏低谐振点10%时，功率因数已经降到0.414，而电源有效利用率更是降到了0.173。

由此可以看出频率对功率因数的影响非常大。仿真结果与前面的理论计算结果相吻合。

5 结束语

通过以上对感应加热原理和影响系统功率因数原因的分析可知，系统功率因数主要是由电容、电感和电源频率这3个参数所共同决定的。而频率对加热效率的影响是非常大的，必须做出调整，使系统工作在谐振频率。负载改变引起的谐振频率改变，传统方法是采用切换电容来改变谐振频率，使其向电源频率靠拢。此法最大的缺点就是电容数量有限，是一些离散的量，无法实现连续调节，从而难以保证系统工作在谐振点附近，以至于功率因数不高，加热效率低。而本文所提到的方式改变电源频率的方法使其向谐振频率靠拢。电源频率在一定范围内是连续可调的，且通过DSP是很容易实现实时跟踪调节，使系统始终工作在谐振点附近，保证了较高的功率因数和加热效率。基于以上原理，本文搭建了MATLAB仿真模型，仿真出频率的改变对加热效率的巨大影响，结果表明中频感应加热器中设计谐振频率自动跟踪系统来提高加热效率的方法正确，有效。

[1]Mauch K.Transistor Inverter for Medium Power Induction Heating Application[M].Canada:AC Statpower Inc.，1986.

[2]罗晓晔，胡美君，丁学恭.一种提升中频加热炉功率因数的原理及方法[J].锻压技术，2007，32(5):160 －164.

[3]潘天明.工频和中频感应炉[M].北京:冶金工业出版社，1983.

[4]孙旭东，王善铭.电机学[M].北京:清华大学出版社，2006:38－34.

[5]陈洪亮，张峰，田社平.电路基础[M].北京:高等教育出版社，2007:476－481.