风电系统中双馈电机直接转矩控制系统的研究

陶彩霞，张友鹏

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

0 引言

随着世界化石能源的匮乏以及环境污染的日趋严重，风能作为一种可再生的绿色能源，越来越多的受到世界上各个国家的关注。其中变速恒频风力发电技术因其高效性和实用性正受到越来越多的重视[1]。为了更加有效的利用风能，提高风力发电系统控制的水平，本文对变速恒频风力发电系统中双馈电机直接转矩控制系统进行了分析研究。

1 双馈风力发电机的基本原理

在风力发电系统中将双馈电机定子接到工频电网上，转子接到四象限变频器上，使定转子同时馈电[2]，等效电路如图1所示。

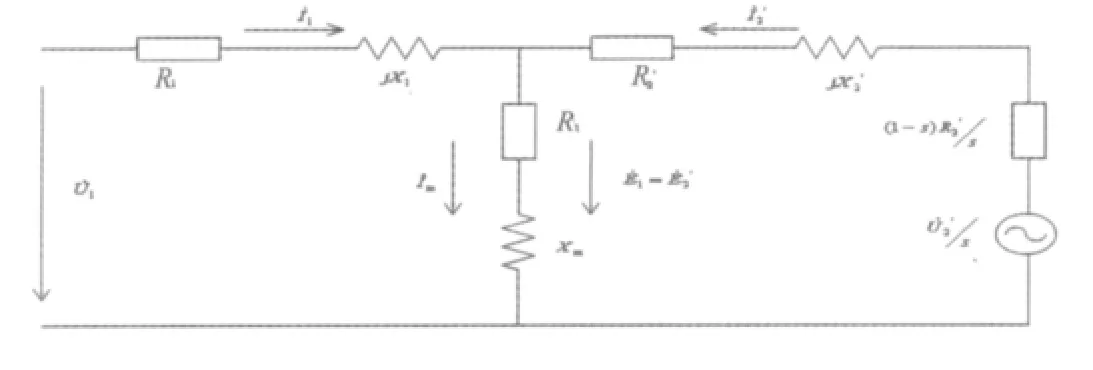
图1 双馈电机等效电路

由等效电路可以得出方程式如下:

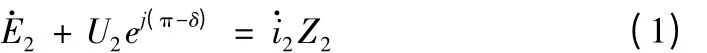
因此转子电流为:

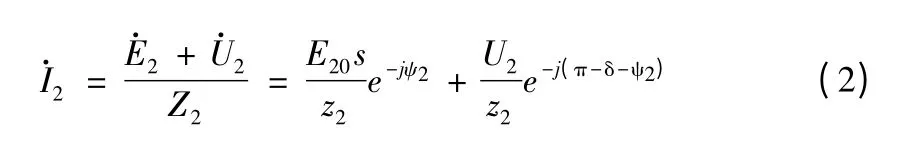
或者:

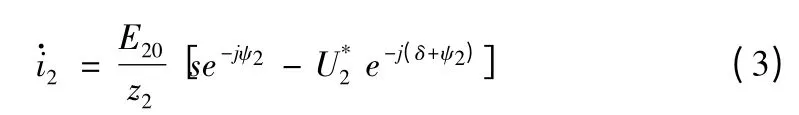
将式(3)展开，可以得到转子电流的有功分量 I2p和无功分量I2q:

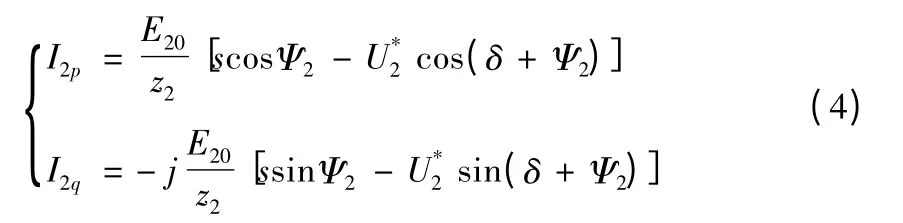
由转子电流的有功分量求出双馈风力发电机的电磁转矩，得:

2 基于圆形磁链的双馈风力发电机直接转矩控制

双馈风力发电机在进行发电时其负载转矩跟随外界风速的变化而实时的变化，所以为了满足并网要求以及外界实时变化的风速，就要控制双馈风力发电机以稳定的转速n运行，实现电磁转矩的实时跟踪。

双馈风力发电机直接转矩控制系统其基本原理就是利用开关型电压逆变器的特点，施加空间电压矢量来控制转子的磁链，通过控制逆变器的六个不同方向的非零电压矢量来使转子磁链沿着圆形轨迹运行，并可通过穿插两个零电压矢量状态来改变转子的转差频率，这样用来控制双馈电机转矩的变化，实现对双馈风力发电机的转速控制[3]。

2.1 转矩方程

根据双馈电机的数学模型，可以得出转矩的方程为:

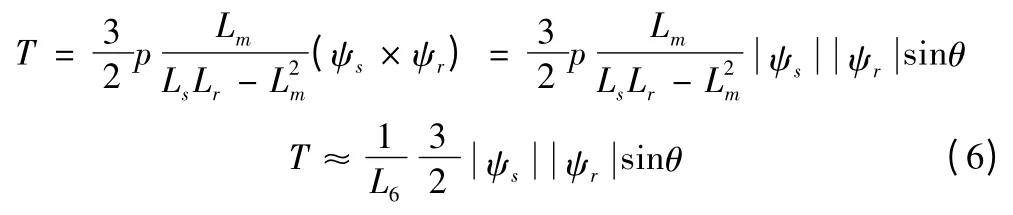
式中，Ls为定子侧自感;Lr为转子侧自感;Lm定转子间互感;Lσ=θ为转子磁链与定子磁链之间的夹角，即磁通角。

根据式(6)可知，双馈风力发电系统的直接转矩控制就是控制双馈电机的转子磁链ψr、定子磁链 ψs、以及定子磁链与转子磁链之间的夹角θ来控制双馈电机的转矩。

2.2 空间电压矢量与转子磁链矢量的关系

在双馈风力发电机直接转矩控制中转子磁链的模型采用u－i模型，表达式为:

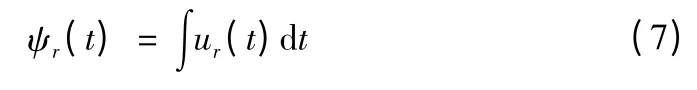
式(7)说明了双馈电机转子空间电压矢量与转子磁链矢量之间的近似关系，将转子磁链矢量与转子空间电压矢量的关系反映到d－q轴上，其运行轨迹如图2所示。

图中ur1(100)～ur6(101)为六个不同方向的非零电压矢量，S1－S6为转子磁链对应的六个扇区;据图2所示，可以分析其沿着整个圆形转子磁链轨迹运行的过程[4]，θ及T随实际风况的变化而变化[5]。

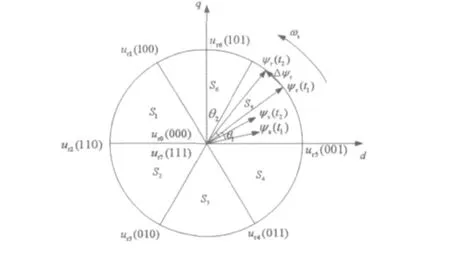
图2 空间电压矢量与逆变器的开关状态的关系图

2.3 逆变器开关状态

最优逆变器开关状态列表如表1所示。

表1中，ψq表示磁链控制信号，当ψq=1时，表示需要增加磁链幅值;当ψq=0时，表示需要减小磁链幅值。Tq为转矩控制信号，当Tq=1时，表示需要增加转矩;当Tq=0时，表示需要发送零电压矢量，以减小转矩;当Tq=－1时，表示需要发送使定子磁链反向旋转的电压矢量，使电机的输出转矩快速减小，加快电机对转矩的响应速度。

2.4 转矩调节器

施密特三点式转矩调节器结构图如图3所示。转矩三点式调节器容差范围为±εm。其中T*为转矩的输入信号的给定值(该值可以通过功率输出曲线以及风能的最大捕获能力查出)，T为实际的转矩，ΔT为输入的给定转矩与实际转矩之间的信号差，Tq为转矩的输出信号。

表1 逆变器开关状态

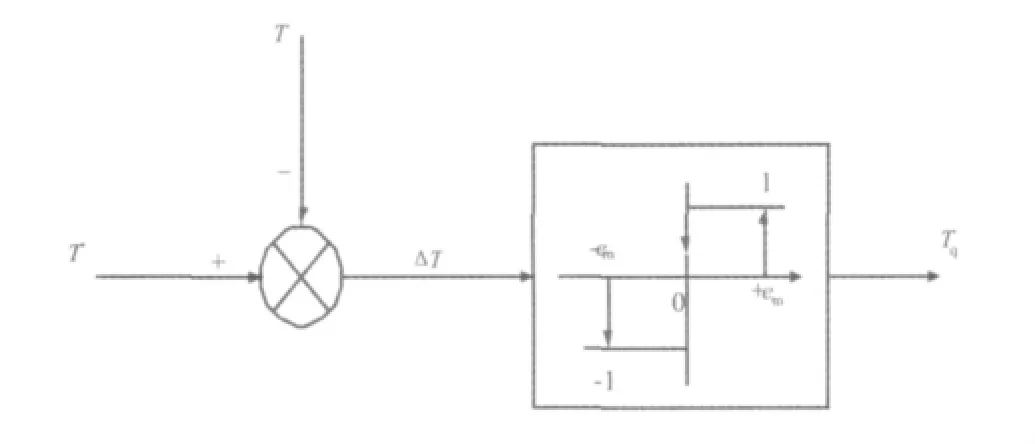
图3 转矩三点式调节器

3 系统仿真

根据系统的基本原理，运用MATLAB/simulink仿真软件搭建近似于圆形磁链的变速恒频风力发电系统直接转矩控制闭环系统的仿真模型。主要包括:风力机模型[6]、双 PWM变换器模型、双馈风力发电机模型、转子的转矩和磁链的检测模型、磁链调节器、三点式转矩调节器、PI控制模型、开关状态选择单元、磁链区间选择单元等。

设置仿真参数如下:

(1)双馈电机主要参数为:(各绕组参数为折算后)

极对数nP=2，采用Y/y接法，额定功率PN=110 kW，额定转速nN=1 785 r/min，定子侧额定电压 UN=575 V，频率 fN=60 Hz，转子电阻 Rr=0.008 913(pu)，转子漏感 L1r=0.054 1(pu)，定子电阻 Rs=0.015 53(pu)，定子漏感 L1s=0.054 1(pu)，定、转子互感 Lm=2.04(pu)，转差率 s= －0.09，摩擦因数 F=0.006 613，惯性常数 H=0.317 5。

(2)风力机的主要参数为:

风力机的叶尖速比 λopt=8.1，最大风能利用系数 Cpmax=0.48，输出的额定功率为:PNmec=100 kW。

功率的基准值为:PB=110 kW;电压的基准值为:UB=电流的基准值为:

3.1 电网电压恒定情况下的仿真结果

假设电网电压是理想的正弦交流电压。在整个过程中给定的风速为vwind=10 m/s，此时发电机的最佳转速为双馈风力发电机同步转速的1.09倍，双馈风力发电机工作在超同步运行状态[7]，转子磁链轨迹仿真图如图4所示。

由图4可知转子磁链的轨迹为近似圆形，其中横轴为转子磁链在d轴上的坐标分量、纵轴为转子磁链在q轴上的坐标分量，单位为 wb。因为磁链模型在每个扇区内都采用了多个空间电压矢量，这样可以减少转矩的脉动以及谐波的含量。

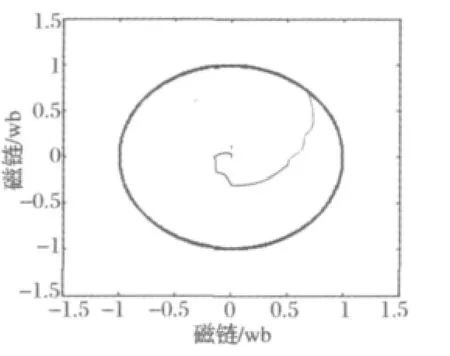
图4 转子磁链轨迹

图5 可以看出在电网电压恒定情况下，整个系统运行比较平稳。

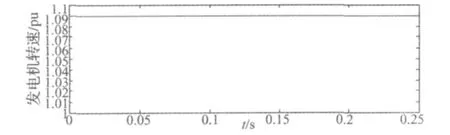
图5 双馈风力发电机转速波形

3.2 电网电压跌落情况下的仿真结果

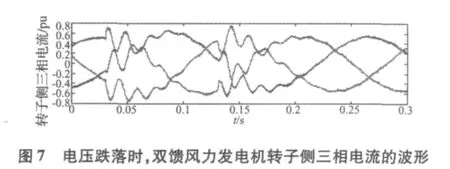
设置风速为vwind=10 m/s，双馈风力发电机同样在超同步转速的状态下运行，在 0.03 s～0.13 s之间，设置电网电压跌落20%。在0.13 s以后又恢复到初始值。仿真波形如图6～图8所示。

由图6～图8可以看出，在电网电压发生跌落时双馈电机定、转子侧的电压及电流也发生了突变，当0.13 s电网电压恢复初始值之后整个系统又恢复到初始状态运行。

由图8可以看出该系统调速性能的优越性，双馈风力发电机一直在指定的转速值附近运行，这样可以更有效的利用风能。

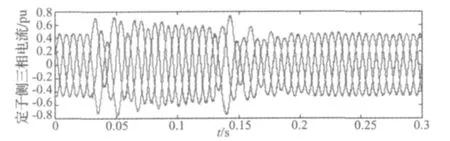
图6 电压跌落时，双馈风力发电机定子侧三相电流波形

4 结束语

论文主要是根据目前的风力发电水平，将直接转矩控制应用到风电系统中，采用近似圆形磁链的空间电压矢量的选择方案，有效解决了转矩的脉动大以及电流谐波含量大等问题。同时转矩调节器采用的是施密特三点式调节器，这样更细化了转矩的偏差分析，提高了系统的性能。

[1]林波，宋平，岗赵芳 .双馈电机变速恒频风力发电技术概述[J].船电技术，2008，28(2):108 －111.

[2]姚兴佳，井艳军，王文卓，等.双馈风力发电机直接转矩控制的研究[J].沈阳工业大学学报，2006，28(6):671－674.

[3]林成武，上风翔，姚兴伟.变速恒频双馈风力发电机励磁控制技术研究[J].中国电机工程学报，2003，23(11):122 －125.

[4]唐浦华，黎亚元.基于圆形磁链轨迹的感应电机直接转矩控制分析[J].电气自动化，2007，29(6):17 －20.

[5]DOMENICO C，GIOVANNI S，ANGELO T.Implementation of a direct torque control algorithm for induction motors based on discrete space vector modulation[J].IEEE Transactions On Power Electronics，2000，15(4):769－777.

[6]Richardson R D，Mcnemey G M.wind energy systems[J].IEEE Transactions On Power Electronics，1993，8l(3):378 － 389.

[7]Arnalte S，Burgos J C，Rodriguez A J L.Direct Torque Control of a Doubly Fed Induction Generator for Variable Speed Wind Turbines[J].Electric Power Component sand Systems，2002，30(2):199－217.