位移反分析的模式搜索支持向量机方法及其应用

刘 永，张志军，贺桂成，丁德馨

(南华大学 核资源与核燃料工程学院，衡阳 421001)

围岩力学参数的合理确定，对于评估地下工程围岩的稳定性及工程安全性，都具有极其重要的意义[1]。常采用位移反分析方法确定围岩的力学参数。传统的位移反分析方法，如解析解法、逆解法、图谱法、弹塑性模型、流变模型等[1-3]，是通过建立围岩力学参数与围岩位移间的数学、力学模型，反演确定围岩力学参数。反分析模型非常复杂，计算量极大，求解难度亦非常大[4]。而基于智能化方法的位移反分析方法，如神经网络算法[5]、优化算法[6]、自适应神经模糊推理方法[7]、粒子群算法[8]、支持向量机算法[9]及各种智能方法相结合的方法等[10-11]，设计原理均是由数值模拟计算结果获得位移反分析所需要的位移量，之后再采用这些智能化方法建立岩石力学参数与位移量之间的拟合关系，进而建立智能化位移反分析方法。这类方法具有较大的创新性，但其在实现过程中各学者均关注于算法的收敛速度和计算精度，而对其结构确定、参数选取、全局最优等关键问题未进行深入研究，存在过多的人为干预，使得智能化方法的智能性无法在真正意义上实现，不同程度地限制了这些智能化位移反分析方法的推广应用。

虽然有着诸多缺点，但这些智能化方法在位移反分析中的应用，已成为学科交叉的一个很好的研究方向，是当前的热门研究课题。为此，研究和建立减少人为干预、便于建模，并能提高收敛速度和预测结果唯一的新智能化位移反分析方法显得尤为迫切[12]。

基于此，本文作者以减少人为干预为前提，先采用 FLAC3D模拟获取围岩力学参数—围岩位移数据对；随后采用模式搜索算法(Pattern search algorithm,PSA)[13]和围岩力学参数—围岩位移数据对构建围岩力学参数与围岩位移间映射的支持向量机模型(Support vector machine, SVM)[14]，从而建立位移反分析的模式搜索支持向量机方法。最后，将该方法应用于反演确定的岩石力学特性参数对实际工程开展数值模拟计算，并将计算结果与长期监测结果相比较，结果表明所建方法是适用的，完全可以满足工程应用需求。

1 位移反分析模式搜索支持向量机构建方法

1.1 位移反分析问题的数学描述

长度方向远大于横断面的地下工程问题均可简化为平面应变问题，那么，对于平面应变状态下的位移反分析问题，需通过量测其一横断面内n个测点处的位移获取现场量测位移向量用来反演确定围岩的力学参数向量b=其中xσ，yσ，xyτ分别为应力，E为弹性模量，μ为泊松比，c为黏聚力，φ为内摩擦角。而实际中，需首先给定若干个力学参数向量通过数值计算得到相对应的若干个模拟位移向量进而建立力学参数向量b与模拟位移向量us之间的映射关系此映射关系即为位移反分析模型，可根据现场量测位移反演确定围岩的力学参数。

本文作者采用SVM来建立力学参数向量b与模拟位移向量us之间的映射关系，从而实现位移反分析。

1.2 支持向量机简介

支持向量机是基于统计学习理论的一种新的学习方法，最早由 Vapnik 教授及其合作者提出[14]，其基本思想是通过用内积函数定义的非线性变换将输入空间变换到一个高维空间，在这个高维空间中寻找输入变量和输出变量之间的一种非线性关系，因此特别适合于解决位移反分析问题。

目前SVM最常用核函数为径向基(RBF)核函数，由于它只有一个参数r，因此成为普适的核函数，并且通过参数的选择，可以适用于任意分布的样本[14]。其关系式如下：

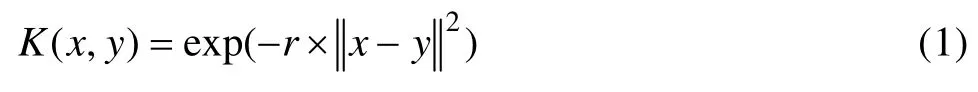
式中：变量r为核函数的参数。

SVM的另一个重要参数为惩罚因子C。关于SVM的这两个参数的确定，到现在为止仍未形成一个统一的模式，只能凭借经验，通过实验对比和大范围搜寻来确定[15]。由于 SVM 的建模存在较多的人为干预，使得其预测结果的唯一性和可靠性难以得到保证。

1.3 支持向量机结构参数的模式搜索算法

模式搜索算法是一类特殊的直接搜索算法[13]。直接搜索算法是一种求解优化问题的方法，它不需要目标函数的梯度信息。与使用梯度或高阶导数信息来搜索优化点的优化算法相反，直接搜索算法搜索当前点周围的一系列点，寻找目标函数值低于当前点值的那些点。可以处理边界约束、线性等式、线性不等式等问题，并且不需要目标函数可微或连续。而PSA以其简洁的算法流程成为应用最为广泛的一种直接搜索算法，它可以确定一个点的序列，并使这个点的序列呈现出越来越接近理想点的趋势。该算法在每一个计算步中，通过把当前点与一个称为模式的固定向量集的标量倍数相加，形成当前点周围的一系列点，即构成一个网格，再对此一系列点进行搜索。如果算法在网格中找到一个新点，且在该点的目标函数值优于当前点的，则算法自动将新点作为下一步搜索的当前点重复计算过程[16]。因此，PSA非常适合于处理目标函数不可微、不连续的问题。

对于SVM这种多参数系统(关键参数为核函数的参数r和惩罚因子C)，这两个参数的不同组合形式影响算法的结果，而合理确定参数组合则极其复杂。这是因为参数组合中的参数之间是相互独立的，并不具有任何线性或非线性的相互联系，但这些单个的参数却同样影响着系统的性能。由此可见，PSA的特性极适合于解决 SVM 的这种多个参数设定问题。因此，本文作者采用PSA来搜索SVM核函数的参数r和惩罚因子C，研究和建立一套适用于 SVM 模型结构确定、训练参数选取及全局最优结果搜索的规则，同时提高模型的收敛速度和保证模型反演结果的唯一性和可靠性，从而建立新的位移反分析的模式搜索支持向量机方法。

1.4 位移反分析模式搜索支持向量机的构建方法

根据上述数学描述及 SVM 的特点，位移反分析的模式搜索支持向量机方法的构建方法如下。

1)测量地下工程某个断面内的位移，获得位移向量um，包括顶、底板竖向位移量和两帮收敛位移量等。

2)依据该地下工程的实际情况，确定围岩力学参数取值范围和取值水平，再采用正交试验设计法确定力学参数向量bi(i=1, 2, …,m)。

3)建立该地下工程的数值计算模型，分别计算与每组力学参数相对应的模拟位移向量(i=1, 2, …,m)，作为SVM的特征参数。

4)按SVM的输入数据格式组成学习数据对和检测数据对。

5)设置初始SVM模型的核函数K和惩罚因子C，分别建立输出目标为E、μ、c、φ、LC(侧压力系数)、SC(剪应力系数)的6个初始SVM结构Si，并设定检测误差阈值。

6)在有检测数据指导的情况下分别对该 6个初始SVM结构进行训练学习，并采用PSA对SVM模型的核函数K和惩罚因子C进行搜索，以获得如下6个映射关系：

7)重复步骤5)和步骤6)，直到检测误差小于或等于阈值时，所得映射关系即为最终的6个模型结构Si，i=1, 2, …, 6。

8)将现场量测位移向量um输入上述6个映射关系Si，其中(i=1, 2, …, 6)，即可得到该地下工程围岩的力学参数向量b，也即为反演结果。

2 位移反分析模式搜索支持向量机的应用

2.1 工程概况

湖南省某地下矿山盛产锡矿，锡矿体赋存于透性较高的七里江灰岩顶部砂化岩石中，其上覆盖着透性极差的页岩。整个矿田构造为一个两端倾伏双攀型短背斜。轴向北东25°，北端为扬起倾伏，倾伏角10°～15°；南端为沉降倾伏，倾伏角 30°～40°。核部由七里江砂化灰岩石组成，北、东、南三面依次变为上泥盆统地层，倾角一般为 20°～30°。西翼为西部大断层破坏，致使石磴于灰岩与七里江砂化灰岩石接触，与七里江砂化灰岩倾角陡变到45°～60°，构成不对称的短背斜。主要发育有F86断层，其走向NE45°、倾向SE、倾角60°左右，属于成矿后断裂，对矿体具有破坏性[17]。

该矿有一赋存于泥盆统佘田桥组中段硅化灰岩中的独立小矿体，且已对这一独立小矿体进行了开采，形成了一长45 m、宽15 m、高6 m的采空区。该采空区上覆岩层厚48 m，表土层厚3 m。采空区以东40 m 处有一倾角为 40°的断层 F86。采空区上方为居民区。该矿已对采空区围岩的变形和开采引起的地面沉陷进行了监测。

2.2 采场围岩位移的计算

1)采场围岩力学参数取值范围的确定

为获取数值建模所需的各种物理力学参数，对矿区围岩样本进行了岩石力学试验。此外，还假定该矿竖向初始地应力的分布符合海姆假设，即σy=γh，其中γ=27.2 kN/m3，则水平初始地应力σx=LC·σy，初始剪应力τxy=SC·σy。因此，待反演的力学参数有6个，分别为E、μ、c、φ、LC、SC。在考虑了该矿区地质资料[17]、国际经验[18]及岩石力学试验结果后，确定了反演参数的取值范围，结果如表1所列。

2)工程围岩位移的量测结果

为了对围岩的力学参数进行反演，同时也为了监测围岩的稳定状况，在矿房长1/2处的横断面内布置测点，分别测量顶底板位移及矿房两边墙收敛位移量，测量结果列于表2。

表1 采场围岩力学参数的取值范围Table 1 Estimated value range of mechanical parameters of rock mass surrounding stope

表2 采场顶、底板及两帮收敛位移量测结果Table 2 Measurements results of displacements on roof, floor and side walls of stope

进一步地，对表1中的岩石力学参数在其取值范围内分为5个水平(如表3所示)，并采用5水平6因素的标准正交表进行正交设计，如表4所列。

3)数值计算模型的建立

依据该矿房的实际尺寸，构建其模型，即取岩石移动角为70°，影响范围X水平方向左边取18 m，右边界则由于断层F86的存在取到86 m处。Z竖直方向起始点取采空区底部向下延伸16.5 m处，上部取到地表岩层边界处。考虑到相邻矿房的尺寸及坐标，该模拟矿房Y水平方向前方取为5 m，矿房长为45 m，后面方向延伸40 m，Y方向共取90 m。所建模型如图1所示。

表3 采场围岩力学参数取值水平Table 3 Levels of mechanical parameters of rock mass surrounding stope

4)模拟计算方案及计算结果

在进行边界约束后，分别以由表4中不同组合下的力学参数进行模拟计算，获得对应的模型计算位移值(矿房沿Y方向长度1/2处断面的位移值，包括顶板、底板的竖向位移量及矿房两边墙水平收敛位移量)，结果如表4所列。

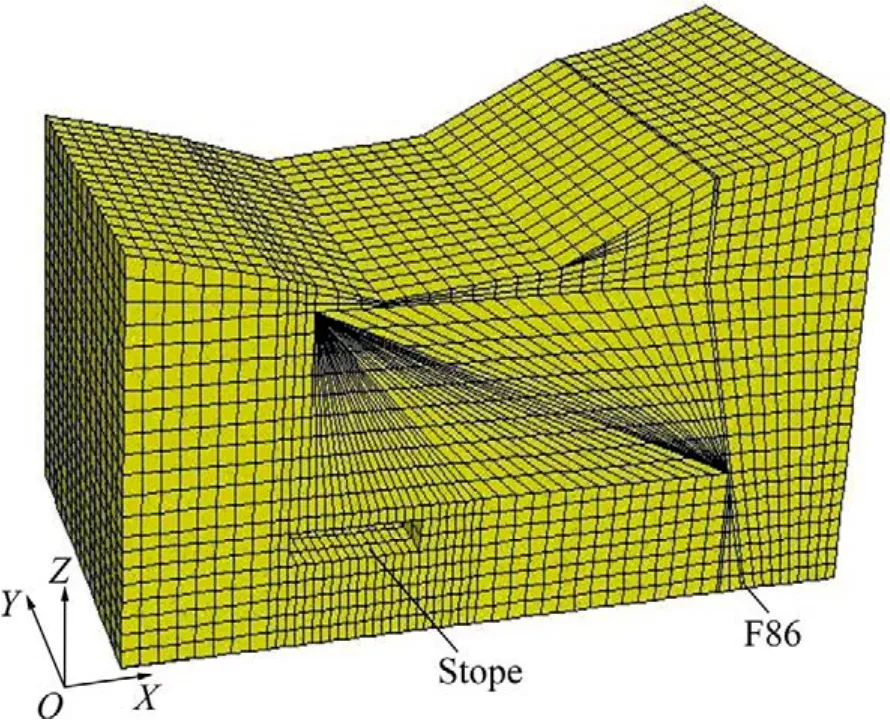
图1 矿房模型图Fig.1 Model of stope

2.3 位移反分析支持向量机的构建

1)数据对的构建

根据PSA和SVM的各自特点，首先建立初始Si结构，其输入特征值均为表4中的模拟位移值，目标输出值为对应的模拟方案的力学参数值，从而实现由位移反演确定围岩的力学参数。由此，即采用模拟位移值与相应的模拟方案的力学参数值分别构建训练(表4中第1～22组数据)和检测数据对(表4中第23～25组数据)。

2)目标函数的确定

根据PSA的特性，需建立相应的目标函数，即将检测数据对(表4中第23至第25组数据)的相对误差作为目标函数值。因此，在本研究中，将目标函数确定为检测数据对的最大检测误差，即将检测数据对输入初始Si，以得到的输出结果与模拟计算值的最大相对误差作为目标函数值，如式(3)所示：

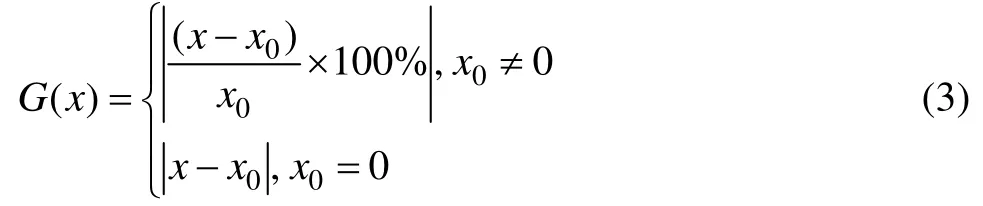
式中：x0为目标输出值；x为预测结果。

3)影响因素的确定及设置

选取SVM的核函数为径向基核函数，其参数r和惩罚因子C为影响训练和预测结果的2个影响因素。另外，2个影响因素为控制网格调整的2个参数[17]，即网格扩展因子(Mesh expansion factor)和网格收缩因子(Mesh contraction factor)。

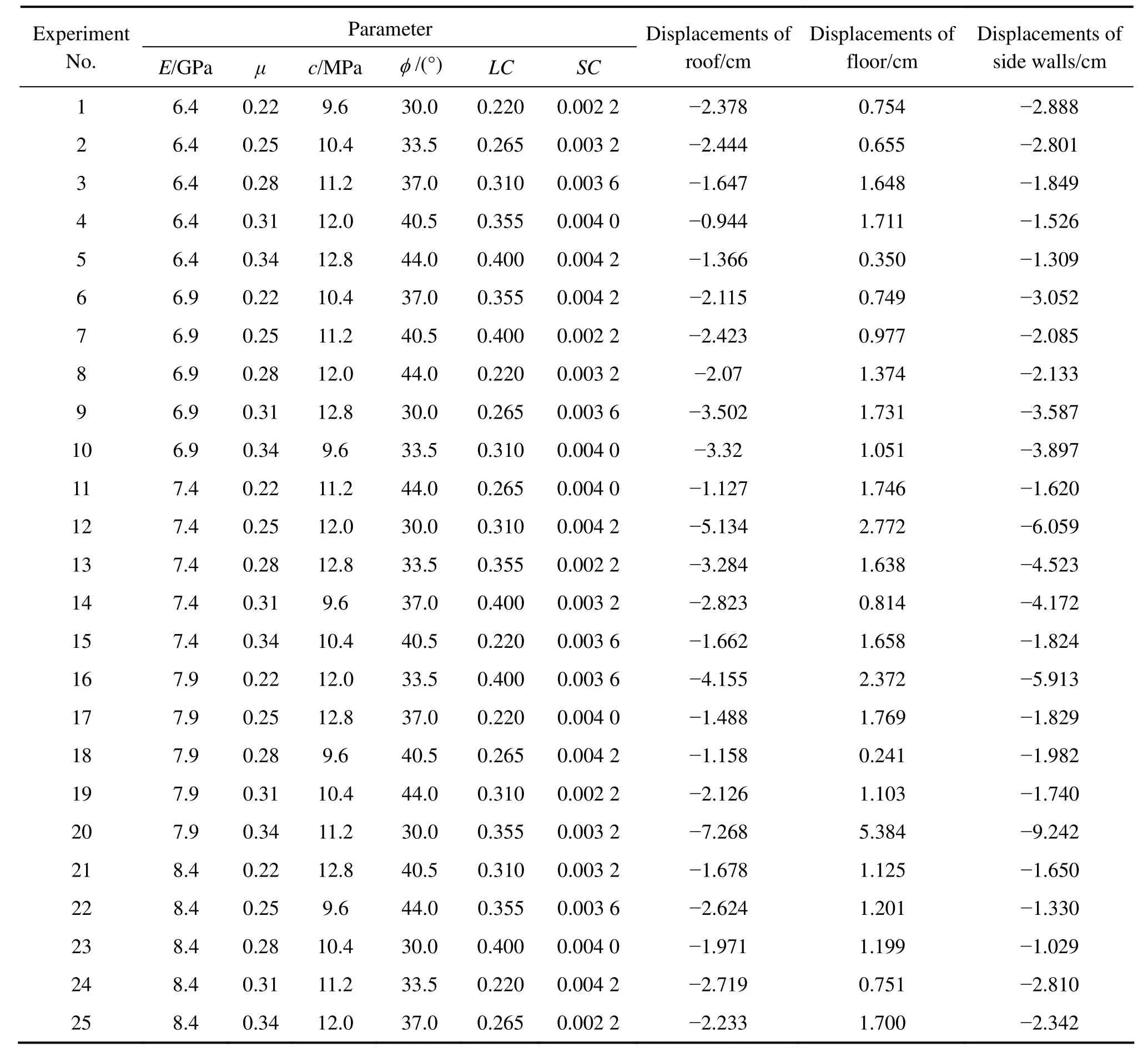
表4 模拟计算方案及计算结果Table 4 Simulation schedule and simulation results

这4个影响因素的取值范围如表5所列，再采用4因素3水平的正交表对该4个因素的取值进行正交设计，各水平取值及正交设计方案如表6和7所列，而最终的参数值选择为表中相对于搜索目标函数最小的一组，即预测效果最好的一组。

表5 4个参数的默认取值及取值范围Table 5 Default value and value range of 4 influencing factors

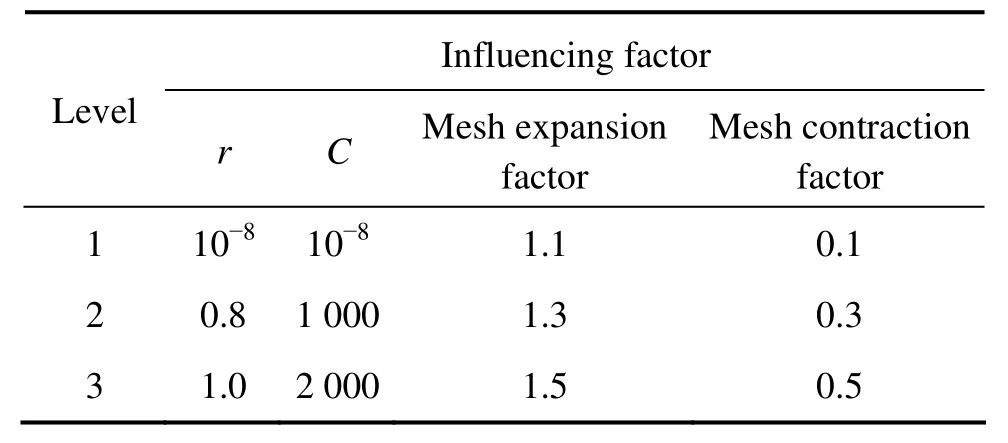
表6 4个影响因素的取值水平Table 6 Value levels of 4 influencing factors

4)支持向量机结构参数的搜索结果

经过对表7的每一组参数进行搜索计算，结果显示，该6个Si结构，对应于搜索目标函数值为最小的参数组合分别为第6、8、5、9、6、8组参数，搜索结果如表8所列。

将表8中搜索得到的核函数参数r和惩罚因子C分别输入所建6个模式搜索—支持向量机中，并采用训练数据对(表4中第1～22组数据)对其分别进行训练学习，所得模型即为各力学参数的最佳模式搜索支持向量机预测模型。

至此，构建了采场围岩力学参数位移反分析的模式搜索支持向量机模型。

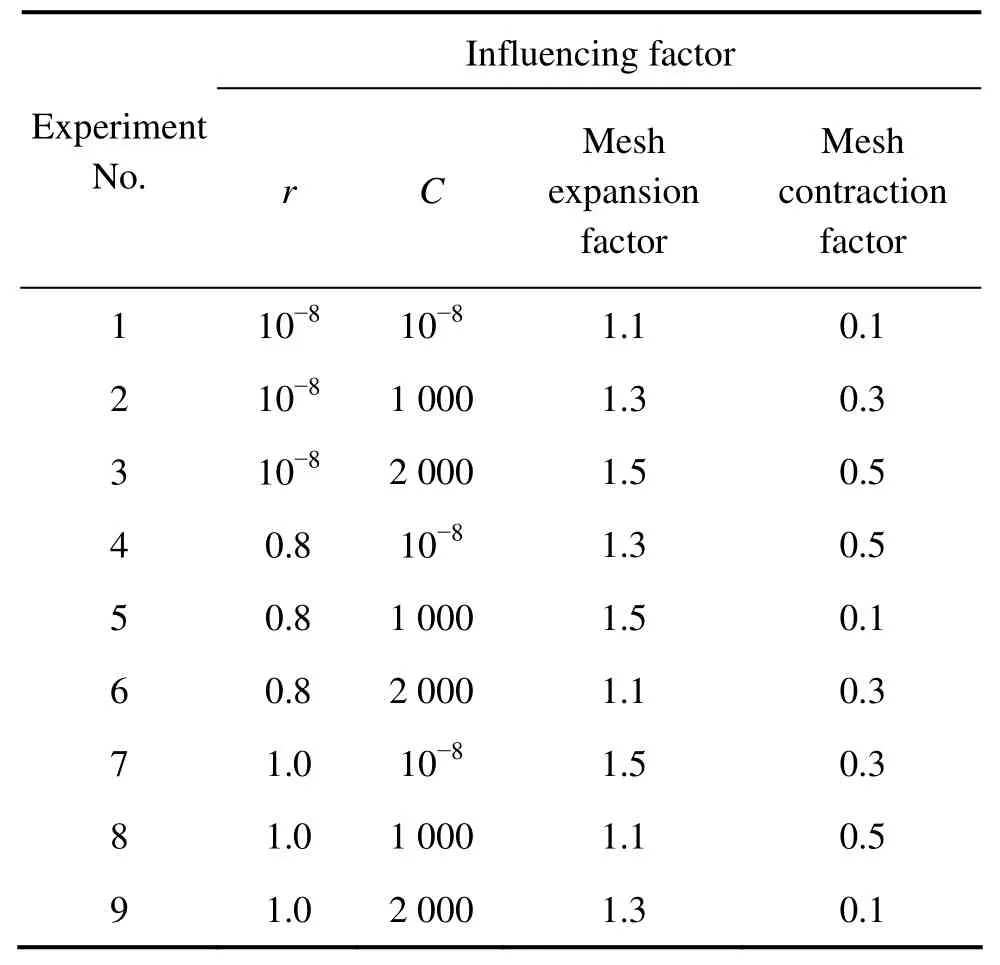
表7 正交试验设计方案Table 7 Orthogonal test design schema

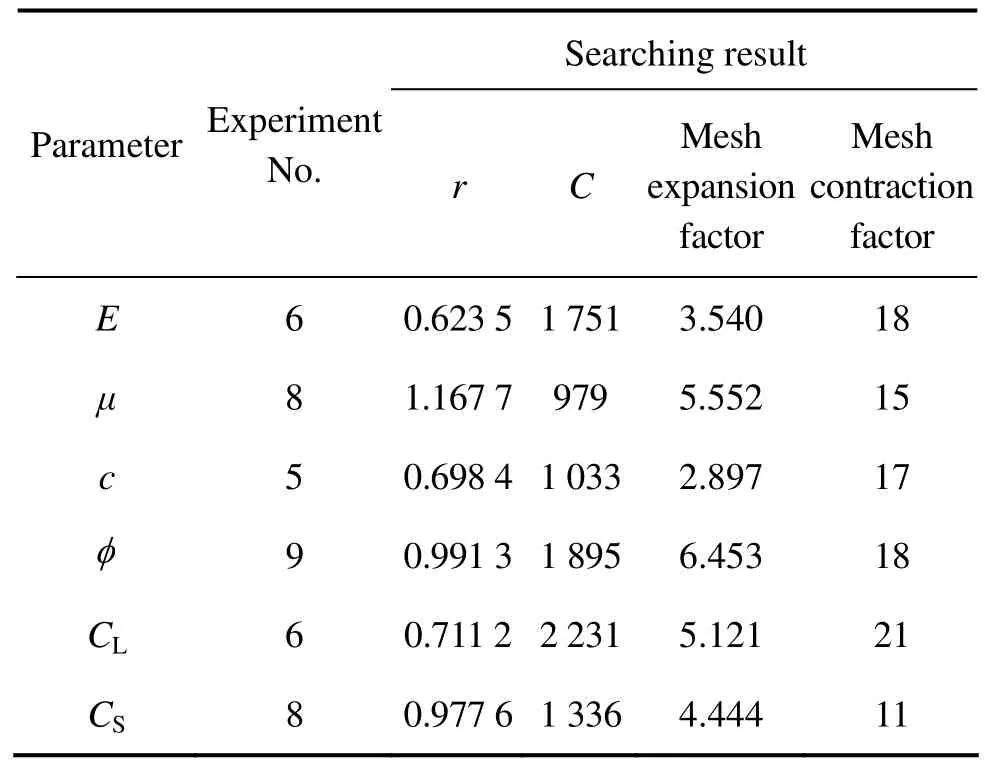
表8 支持向量机结构参数的搜索结果Table 8 Searching results of support vector machine model

2.4 采场围岩力学参数的支持向量机反演

将表2中该矿房顶、底板和两帮收敛位移量监测结果输入所建位移反分析的模式搜索支持向量机模型，其输出即为围岩力学参数的反演结果，列于表9。

表9 地下采场围岩力学参数的反演结果Table 9 Inversion results of mechanical parameters of rock mass surrounding stope

2.5 采场围岩力学参数支持向量机反演结果的检验

为了验证方法的可行性，并确定回采后围岩形变对地表的影响程度，采用表9中所列反演结果，对计算模型进行了模拟计算。进一步地，沿采空区中心，采用自编接口程序，获得了X向矿房1/2处断面(Y=25 m)的竖向模拟位移等值线图如图2所示。

将模型计算中该剖面地表各点沉降量绘制于坐标中，结果如图3。由图3可以看出，模型沿水平方向的地表下沉量呈近似半碗口状曲线分布。在模型坐标X为3.2 m处，沉降量达到最大值2.541 6 cm。

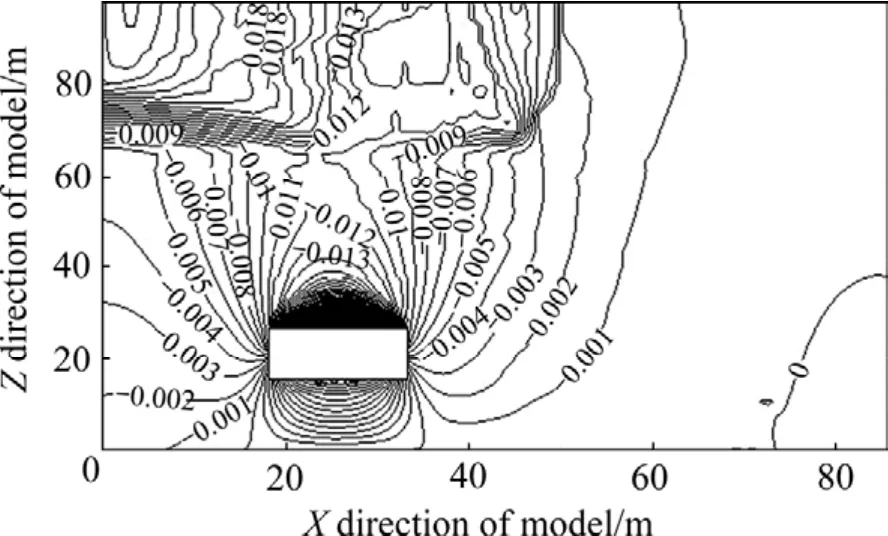
图2 模型X向竖直剖面位移等值线图Fig.2 Vertical displacement isopleths of model along X direction (m)

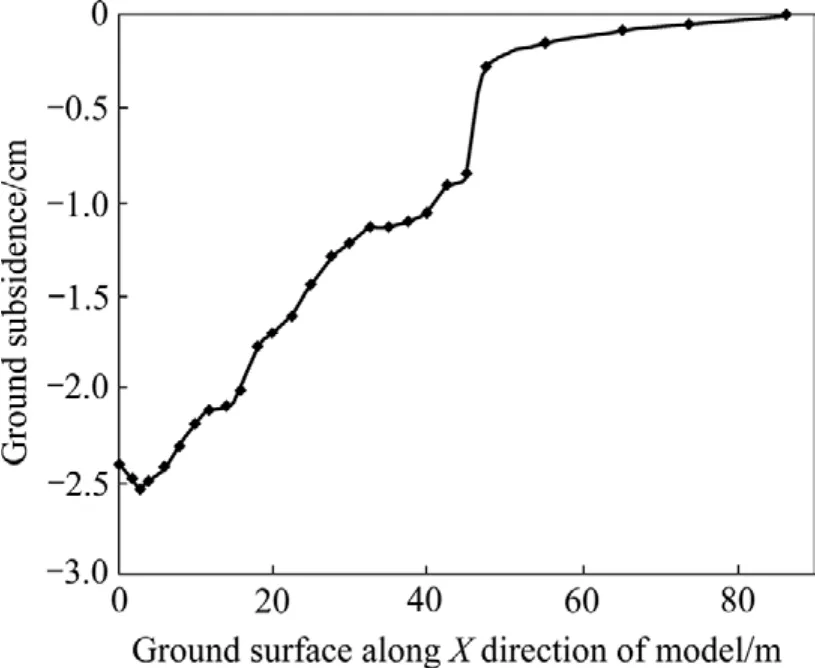
图3 模型地表沉降量曲线Fig.3 Ground subsidence curve of model

为了验证模拟结果，沿模型中该剖面在实际地表布置了多个测点，并进行了长期监测。截止2011年底，监测结果显示，该矿房上覆地表沉降已趋于稳定，且其沉降量最大值为2.560 cm，其位置亦如图3所示，监测结果与模拟结果吻合较好。

3 结论

1)采用模式搜索算法优化支持向量机等方法，建立了一种位移反分析的模式搜索支持向量机(PSASVM)方法。该方法充分利用PSA的寻优性能、SVM的预测性能以及正交设计的优化试验特性，具有模型建立简捷、参数调节明确、推广预测精度高且结果为全局最小等特点，应用于位移反分析中。

2)将所建立的位移反分析的模式搜索支持向量机方法，应用于某矿山矿房围岩岩石力学参数反演中，并采用反演结果对该矿房进行了数值模拟计算，计算结果与实际监测结果吻合良好，有效地验证方法的正确性和工程适用性。

3)以减少人为干预为前提，提出和建立一种更加智能化的位移反分析方法，对于位移反分析智能化研究工作具有重要意义。

[1]王思敬.中国岩石力学与工程世纪成就[M].南京: 河海大学出版社, 2004.WANG Si-jing.Century achievements of rock mechanics and engineering in China[M].Nanjing: Hohai University Press,2004.

[2]MOHAMMAD N, REDDISH D J.The relation between in situ and laboratory rock properties used in numerical modeling[J].International Journal of Rock Mechanics and Mining Sciences,1997, 34(2): 289-297

[3]YANG Zhi-fa, LEE C F, WANG Si-jing.Three-dimensional back-analysis of displacements in exploration adits-principles and application[J].International Journal of Rock Mechanics and Mining Sciences, 2000, 37(3): 525-533.

[4]肖铭钊, 周承豪, 程 芸, 冯晓腊, 杨俊梅.有限元与改进单纯形法联合编程技术在位移反分析中的应用[J].岩土力学,2011, 32(3): 899-904.XIAO Ming-zhao, ZHOU Cheng-hao, CHENG Yun, FENG Xiao-la, YANG Jun-mei.Application of finite elements and modified simplex method jointed programming technology to displacement back analysis[J].Rock and Soil Mechanics, 2011,32(3): 899-904.

[5]王树栋.基于进化神经元算法的堡镇隧道软弱围岩施工弹塑性智能位移反分析[J].北京交通大学学报, 2010, 34(3):112-116.WANG Shu-dong.Elasto-plastic intelligence displacement back analysis of soft rock construction in Baozhen tunnel based on evolutionary-neuron algorithm[J].Journal of Beijing Jiaotong University, 2010, 34(3): 112-116.

[6]伍国军, 陈卫忠, 贾善坡.大型地下洞室围岩体蠕变参数位移反分析研究[J].岩石力学与工程学报, 2010, 29(S2):4043-4049 WU Guo-jun, CHEN Wei-zhong, JIA Shan-po.Displacement back analysis of creep parameters of engineering rock mass in large-scale underground chambers[J].Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 4043-4049.

[7]丁德馨, 张志军.位移反分析的自适应神经模糊推理方法[J].岩石力学与工程学报, 2004, 23(18): 3087-3092.DING De-xin, ZHANG Zhi-jun.Adaptive neuro-fuzzy inference approach for back analysis of displacements[J].Chinese Journal of Rock Mechanics and Engineering, 2004, 23(18): 3087-3092.

[8]苏国韶, 张克实, 吕海波.位移反分析的粒子群优化—高斯过程协同优化方法[J].岩土力学, 2011, 32(2): 510-516, 524.SU Guo-shao, ZHANG Ke-shi, LÜ Hai-bo.A cooperative optimization method based on particle swarm optimization and Gaussian process for displacement back analysis[J].Rock and Soil Mechanics, 2011, 32(2): 510-516, 524.

[9]张凌然, 徐卫亚, 聂卫平, 石 崇, 杨云浩.基于AFSA-LSSVM 的位移反分析方法研究[J].水电能源科学,2011, 29(4): 78-80.ZHANG Ling-ran, XU Wei-ya, NIE Wei-ping, SHI Chong,YANG Yun-hao.Research on back analysis method of displacement based on AFSA-LSSVM[J].Water Resources and Power, 2011, 29(4): 78-80.

[10]徐 飞, 徐卫亚, 梁桂兰, 王 珂.基于连续蚁群算法和小波支持向量机的位移反分析[J].水利水电科技进展, 2009, 29(1):16-19.XU Fei, XU Wei-ya, LIANG Gui-lan, WANG Ke.Displacement back analysis based on continuous ant colony algorithm and wavelet support vector machines[J].Advances in Science and Technology of Water Resources, 2009, 29(1): 16-19

[11]关永平, 宋 建, 王述红, 刘 宇.基于 GA-BP算法的隧道围岩力学参数反分析[J].东北大学学报: 自然科学版, 2012,33(2): 276-278, 283.GUAN Yong-ping, SONG Jian, WANG Shu-hong, LIU Yu.Back analysis of mechanical parameters of surrounding rocks based on GA-BP algorithm[J].Journal of Northeastern University: Natural Science, 2012, 33(2): 276-278, 283.

[12]张志军.PSA-ANFIS方法及其在矿山岩土工程灾害预测中的应用[D].长沙: 中南大学, 2008.ZHANG Zhi-jun.Studies on PSA-ANFIS and its application in predicting the mine geotechnical engineering disaster[D].Changsha: Central South University, 2008.

[13]YANG Y W, SOH C K.Fuzzy logic integrated genetic programming for optimization and design[J].Journal of Computing in Civil Engineering, ASCE, 2000, 14(4): 249-254

[14]VAPNIK V.The nature of statistical learning theory[M].New York: Springer Verlag, 1995

[15]雷英杰, 张善文, 李续武.MATLAB遗传算法工具箱及应用[M].西安: 西安电子科技大学出版社, 2005.LEI Ying-jie, ZHANG Shan-wen, LI Xu-wu.Genetic algorithm toolbox in MATLAB and its application[M].Xi’an: Xidian University Press, 2005.

[16]张 鹏, 倪世宏, 王彦鸿.一种支持向量机更新模型的参数选择方法[J].电光与控制, 2011, 18(9): 87-90.ZHANG Peng, NI Shi-hong, WANG Yan-hong.A method for parameter selection of support vector machine updated model[J].Electronics Optics & Control, 2011, 18(9): 87-90.

[17]湖南省某矿山工程部.湖南省某矿山采空区调查报告[R].2006.A Certain Mine Engineering Department in Hunan Province.An investigative report on mined-out regions of a certain mine in Hunan Province[R].2006.

[18]HOKE E, BROWN E T.Practical estimates of rock mass strength[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1997, 34(8): 1165-1186.