安全系数降低对压力容器可靠度的影响分析

刘芳

（江苏连云港工贸高等职业技术学校机械工程系)

安全系数降低对压力容器可靠度的影响分析

刘芳*

（江苏连云港工贸高等职业技术学校机械工程系)

采用可靠性工程方法（一次二阶矩法）分析了常规设计中安全系数的降低对压力容器的影响。计算表明，安全系数从3.0降低到2.7，压力容器的可靠度变化不大。

压力容器安全系数一次二阶矩法可靠度应力

0 前言

目前压力容器和压力容器用材的国际竞争异常激烈，在保证压力容器安全的前提下，竞争的焦点就集中在压力容器的经济性上。其中最显著的方法是通过降低安全系数来提高材料的许用应力值，从而在相同的设计参数下可以得到较小的壁厚值。我国目前正在开展设计安全系数的研究[1]，初步的方案是在GB 150—1998《钢制压力容器》[2]中相对于抗拉强度的安全系数从3.0下降到2.7。这一改变将影响屈强比在0.6～0.8之间的碳素钢和低合金钢制压力容器的设计选材问题[3]。本文采用可靠性的方法分析安全系数降低对压力容器可靠度的影响。

1 可靠性的分析方法

在可靠性的分析方法中[4]，首先要对失效的物理原因进行分析，寻找失效机理，建立可供计算的物理模型，直到得出失效的可能性。失效物理模型有很多种，其中应力强度-干涉模型是工程中最常用的一种理论模型，其数学表达式为：Z=X-Y。式中Y为结构中最大工作应力，X为结构强度，而结构的可靠度就是计算结构强度高于应力时的概率值，即：

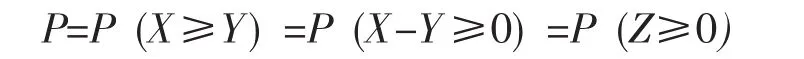
按结构可靠度的一次二阶矩法(FOSM)分析理论，可以用可靠性指标β来衡量结构的可靠度，其表达式为：

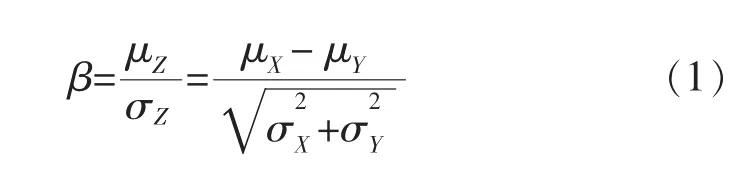
则结构的可靠度

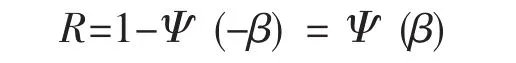
失效概率

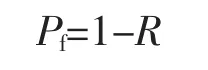
2 实例分析

某内压回转容器，封头形式为标准椭圆封头，设计温度为20℃，筒体和封头材料为16MnR，焊接接头系数φ=0.85。已知设计温度下16MnR的许用应力，在厚度为6～16 mm时，材料的抗拉强度σb=510 MPa；在厚度为16～36 mm时，材料的抗拉强度σb=490 MPa。

2.1 壁厚的计算

《钢制压力容器》常规设计方法中，筒体和标准椭圆封头壁厚的计算公式分别为：

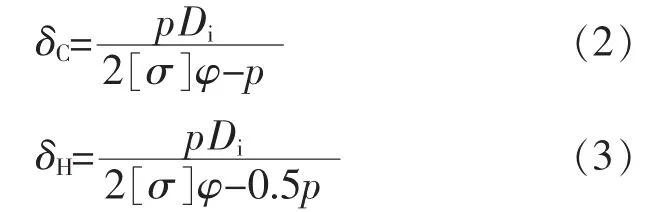
2.2 可靠度的计算

为了得到结构的可靠度，假设各参量均服从正态分布：此筒体的工作压力值就为其设计压力值，且其变异系数Crp=0.05，筒体直径的变异系数CrD=0.002，筒体壁厚的变异系数Crt=0.1，屈服强度的变异系数Crs=0.2。受内压的椭圆形封头中的应力，包括由内压引起的薄膜应力和封头与圆筒连接处不连续应力。

由压力容器的应力分析计算公式可知，筒体的最大应力为环向应力σθ，即结构最大工作应力为：

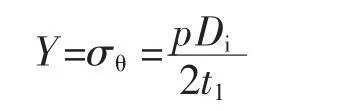
t1为筒体的实际壁厚，则应力的均值为：

式中，μ代表均值，其下标代表各参量。应力的标准差为：

屈服强度的均值为：

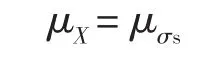
屈服强度的标准差为：

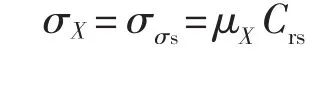
2.3 不同设计压力条件下抗拉强度安全系数的影响

下面讨论不同设计压力条件下，抗拉强度安全系数降低对结构的影响。

2.3.1 基于无力矩理论的可靠度计算

现假定筒体的内径Di=1 000 mm，选取不同的设计压力，即在设计压力为1 MPa、2 MPa、5 MPa、8 MPa时，分别计算条件（1）和条件（2）时的计算厚度、β值及失效概率，列于表1、表2中。

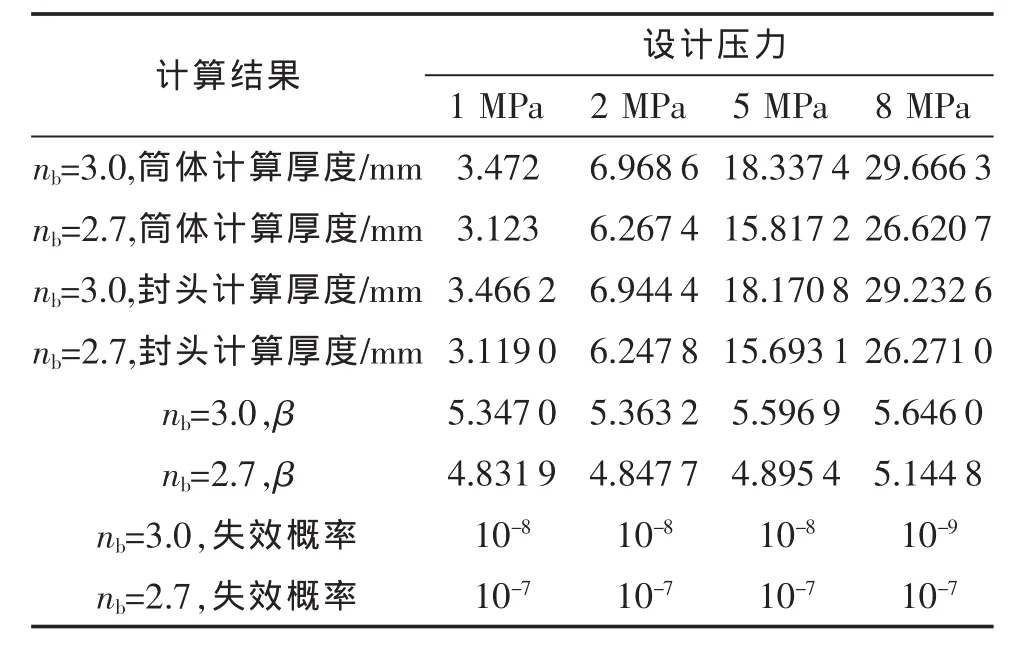
表1 不同的nb和设计压力条件下容器的失效概率

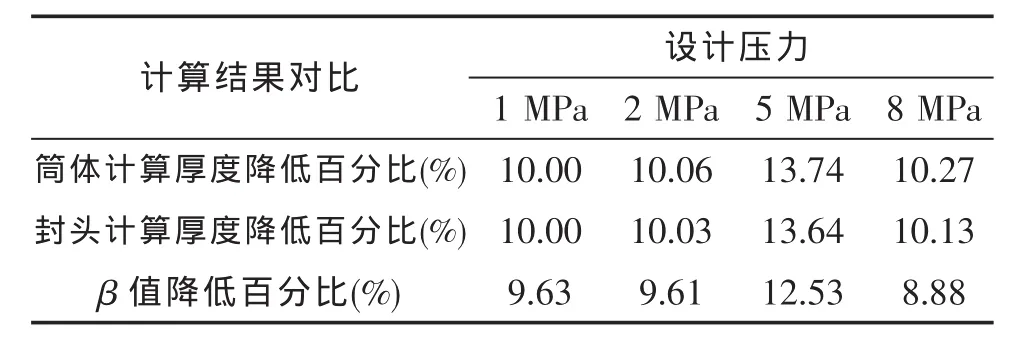
表2 不同的nb和设计压力条件下计算结果对比

由表1、表2的结果可知，常规安全系数降低10%，在不同的设计压力下计算得到的筒体厚度和封头厚度相应地降低了10%左右，β值降低9%左右，而失效概率从10-8～10-9微升到10-7。

2.3.2 考虑局部应力的可靠度计算

本文前面所述的筒体和封头的可靠度计算，均是按照薄膜应力进行的，但实际上，标准椭圆封头与圆柱壳连接时，将产生不连续效应，在这些壳体的边缘同样存在边缘应力和边缘力矩。为此，有必要进行边缘应力处的可靠度验算。

按照JB 4732[6]的原则，将应力进行分类。受内压的圆筒与封头的连接处的应力类型包括一次总体薄膜应力Pm、一次弯曲应力Pb、一次局部薄膜应力PL和二次应力Q。根据安定性分析，一次应力加二次应力的应力强度SⅣ的许用应力值为3Sm，即SⅣ≤3Sm。因此，建立的相应应力-强度干涉模型为：

式中，Sm为JB 4732中的许用应力值，对于低碳钢根据文献[7]可知，筒体与封头连接处的最大应力值

根据概率论的相关知识，将本文前面计算所得到的结果代到应力-强度干涉模型公式中，分别验算条件（1）和条件（2）时边缘应力区的可靠度值，并将结果汇于表3中。

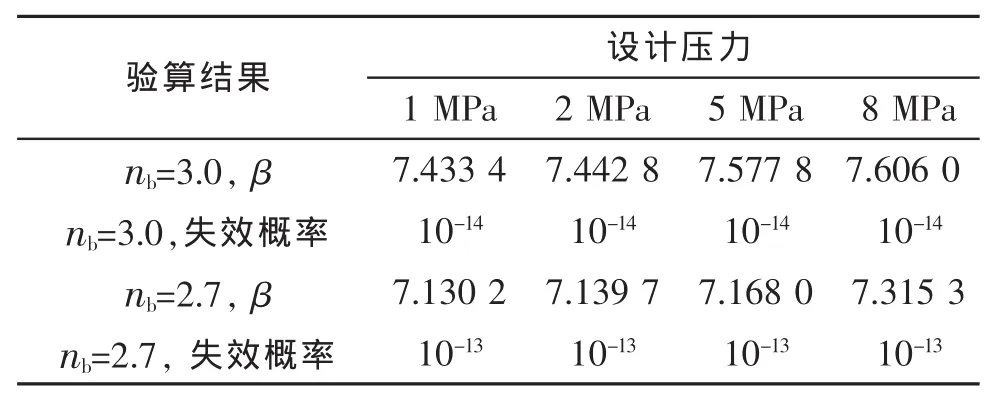
表3 不同设计压力下考虑局部应力的结构可靠度

由表3可知，不同的设计压力条件下，抗拉强度安全系数nb从3.0降低到2.7，对于封头与筒体连接处的局部应力，按照安定理论验算的失效概率从10-14～10-15微升到10-13。

综合考虑表1～3的计算结果，抗拉强度安全系数降低10%，无论是按照薄膜应力计算的失效概率，还是按照安定理论验算的、考虑局部应力后容器的失效概率，均小于文献[8]中所述的关于Ⅲ类压力容器失效概率的下限值。因而，压力容器常规设计中的抗拉强度安全系数nb从3.0降低到2.7是合理的。

3 结论

降低常规设计中的抗拉强度设计安全系数，可以有效降低设备的设计成本，提高其在市场中的竞争力。而降低安全系数后，容器可靠度值变化不大。所以我国拟将常规设计中抗拉强度设计安全系数从3.0降低到2.7是可取的。

[1] 马利，郑津洋，寿比南，等.奥氏体不锈钢制压力容器强度裕度研究[J].压力容器,2008（1）.

[2] GB 150—1998.钢制压力容器[S].

[3] 黄嘉琥,王为国,寿比南,等.各国压力容器用材确定许用应力方法的比较[J].压力容器,2008（4）.

[4] 戴树和.工程风险分析技术[M].北京：化学工业出版社，2007.

[5] 郑津洋，董其伍，桑芝富.过程设备设计[M].北京：化学工业出版社，2005.

[6] JB 4732—1995.钢制压力容器——分析设计标准[S].

[7] 王志文,蔡仁良.化工容器设计[M].北京：化学工业出版社，2003.

[8] 赵建平.压力容器概率安全评定失效准则研究[J].化工设备与管道,2000（5）.

Effect of Reduced Safety Factor to Pressure Vessel Reliability

Liu Fang

Using FOSM(first order second moment)to analyze the effect of reduced safety factor to reliability in conventional design.Calculations show that the safety factor decrease from 3.0 to 2.7 is reasonable.

Pressure vessel;Safety factor;FOSM;Reliability;Stress

TQ 050.2

*刘芳，女，1984年生，助理讲师。连云港市，222061。

2011-10-12）