自增强圆筒塑性区深度和承载能力探讨*

朱瑞林朱国林

（湖南师范大学工学院)（江西警察学院基础部）

自增强圆筒塑性区深度和承载能力探讨*

朱瑞林**朱国林

（湖南师范大学工学院)（江西警察学院基础部）

从限制弹塑性界面处总应力的当量应力与内壁面处卸除自增强压力后的残余应力的当量应力出发，探讨了厚壁圆筒的塑性区深度和承载能力，提出了相关的计算公式和图表。

厚壁圆筒自增强超应变度承载能力压力容器

0 前言

自增强可提高厚壁圆筒的承载能力，并且通常认为，对于自增强容器，弹塑性界面处总应力的当量应力是危险的，必须加以限制[1-2]。但研究证明，自增强处理时施加的压力太大，也会有不利影响[3-5]。而自增强压力的大小直接影响塑性区的深度（超应变度），超应变度的大小又影响着承载能力。因此有必要同时考虑弹塑性界面处总应力的当量应力和卸除自增强压力后筒体内壁面上的残余应力，来研究自增强压力和承载能力的问题。

本文基于第四强度理论，同时假定：

①容器材料是完全弹塑性的，包辛格（Bauschinger）效应不计，压缩屈服强度等于拉伸屈服强度。

②不计应变硬化。

③材料没有缺陷。实际材料可在本文的结果上加以修正。

1 理论分析

文献[3]曾导出一个经自增强处理卸除自增强压力后残余应力的当量应力不超过屈服强度（|σei′/σy|≤1），即不发生反向屈服的塑性区深度公式：

式中，e0.5≤kj≤kc=2.218 457 489 916 7…，同时k≥2.218 457 489 916 7…。由于

时，无论kj多大，也不会有σei′/σy≤-1，因此本文下述讨论都是针对k≥2.218 457 489 916 7…的情况。关于数据2.218 457 489 916 7…的来历可参考文献[3]。式（1）可绘制成曲线图，见图1曲线1。

文献[2]曾导出一个使弹塑性界面rj处总应力的当量应力最小的塑性区深度公式：

最大弹性载荷

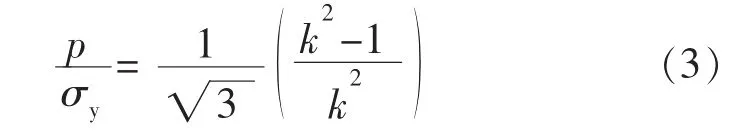
将式（3）代入式（2）得

当kj按式（4）计算时，可使rj处的总应力的当量应力最小。式（4）的图像见图1曲线2。由式（4）和图1可知，随着k增大，kj亦增大，kj的极限值是而由式（1）和图1可知，随着k增大，kj是减小的，式（1）中kj的极限值也是这就是说，由式（1）确定的kj比由式（4）确定的要大，即由式（4）来确定的kj永远不会发生反向屈服，即|σei′/σy|≤1，但仅限于承受最大弹性载荷。但是容器仅承受最大弹性载荷时，自增强就没有意义，不进行自增强处理的容器也能承受式（3）所示的载荷。

图1 kj与k的关系

由式（2）得承载能力与塑性区深度的关系：

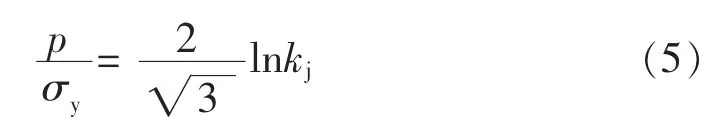
满足式（5）要求时，可保证rj处的总应力的当量应力最小。如果这时塑性区深度按式（1）确定，式（1）和式（5）联合，承载能力是一个隐式，其图像如图2曲线1所示。曲线1可同时保证rj处的总应力的当量应力最小和不发生反向屈服，即|σei′/σy|≤1。由图2可见，随着k增大，承载能力是下降的，k趋于∞时，承载能力的极限是而这又恰是最大弹性载荷，即式（3）的极限，见图2曲线2。

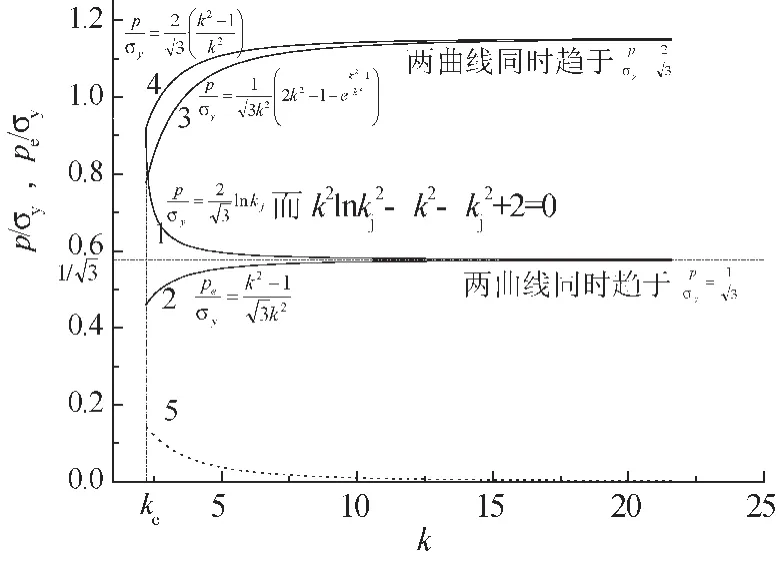
图2 承载能力与k的关系

研究表明，“rj处的总应力的当量应力最小”并不是很值得追求的目标。由文献[3]可知，一般地，rj处的总应力的当量应力最小时，该应力比屈服强度小不少，如果允许rj处的总应力的当量应力接近或达到屈服强度，可以提高承载能力。当σej/σy=1时，由文献[3]可知，

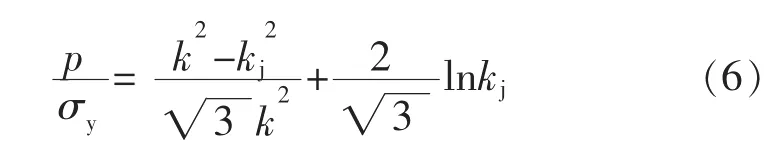
如果让容器产生式（4）所示的塑性区深度，将式（4）代入式（5），则承载能力

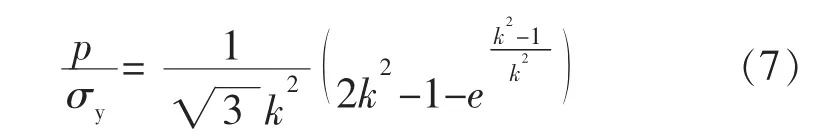
这个承载能力就比最大弹性载荷大多了，而这时虽然rj处总应力的当量应力不是最小，但没有超过屈服强度，同时有|σei′/σy|≤1。不过，这个承载能力比之于文献[3]所建议的

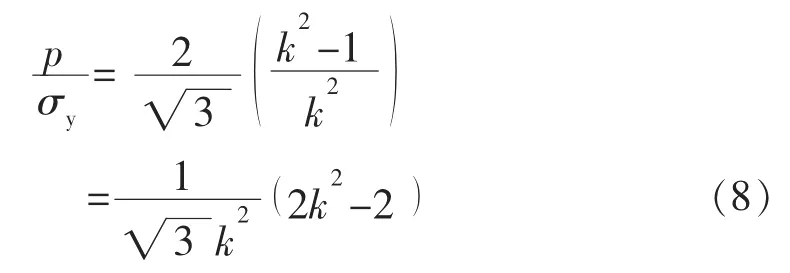
要小。因为，

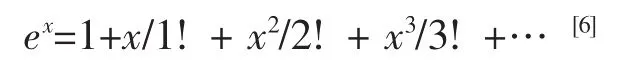
为什么会这样呢？因为由式（4）确定的kj比由式（1）确定的小，而式（1）是刚要发生反向屈服，即|σei′/σy|=1的塑性区深度，塑性区深度浅，承载能力就小。所以由式（7）确定承载能力还没有充分发挥容器的承载潜力。而文献[3]所建议的承载能力计算式

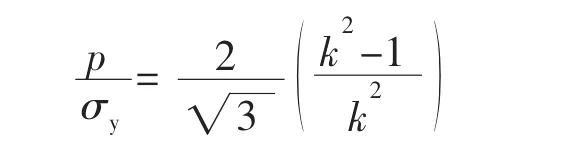
但需注意：塑性区深度小可能导致rj和/或ri处总应力的当量应力过大。因为塑性区深度小，自增强处理后的残余压应力小，当与工作应力叠加时，会使总应力的当量应力增大。当容器受载超过式（6）所示的值时，将使σej/σy>1，σei/σy>1。文献[3]曾给出下述若干公式。

rj处总应力的当量应力：

rj处残余应力的当量应力：

ri处总应力的当量应力：

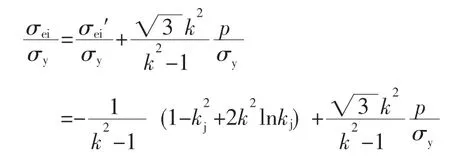
ri处残余应力的当量应力：

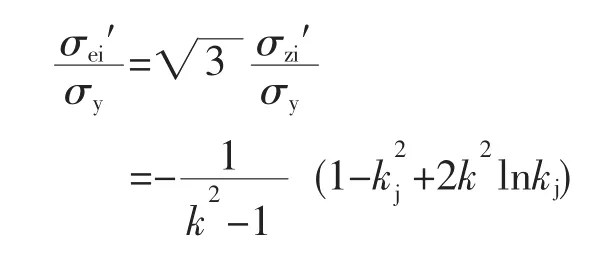
其中σzi′为内壁面处轴向残余应力。

令σej/σy>1，σei/σy>1，均得到：

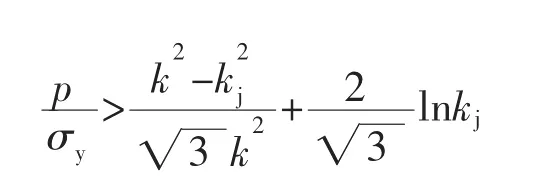
由图2还可以看到k>5后，增加厚度对提高承载能力几乎不起作用。

塑性区深度也常用超应变度来衡量。超应变度的定义是：

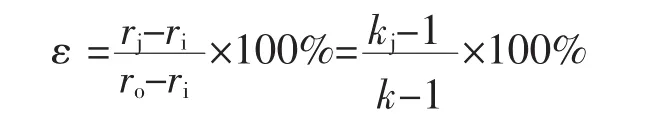
或

将式（9）代入式（1）得：

k2ln[ε(k-1)+1]2－k2－[ε(k-1)+1]2+2=0(10)式（10）关联了一定超应变度ε下的最大壁厚k，或一定壁厚k下的最大超应变度ε。这是一个隐式，可将其图像绘于图3。

图3 ε与k的关系

k≤kc=2.218 457 489 916 7…时，超应变度ε可达100%，即整体屈服，k越大，ε越小。

将式（10）或式（9）分别与式（8）、式（7）和式（2）结合，可得三种情况下的承载能力，这些表达式都是隐式，其图像绘于图4的曲线1、2、3。可以利用图4来确定一定超应变度下的承载能力。为方便和精确计，将ε、k和p/σy的数值关系列于表1。

图4 承载能力与超应变度的关系

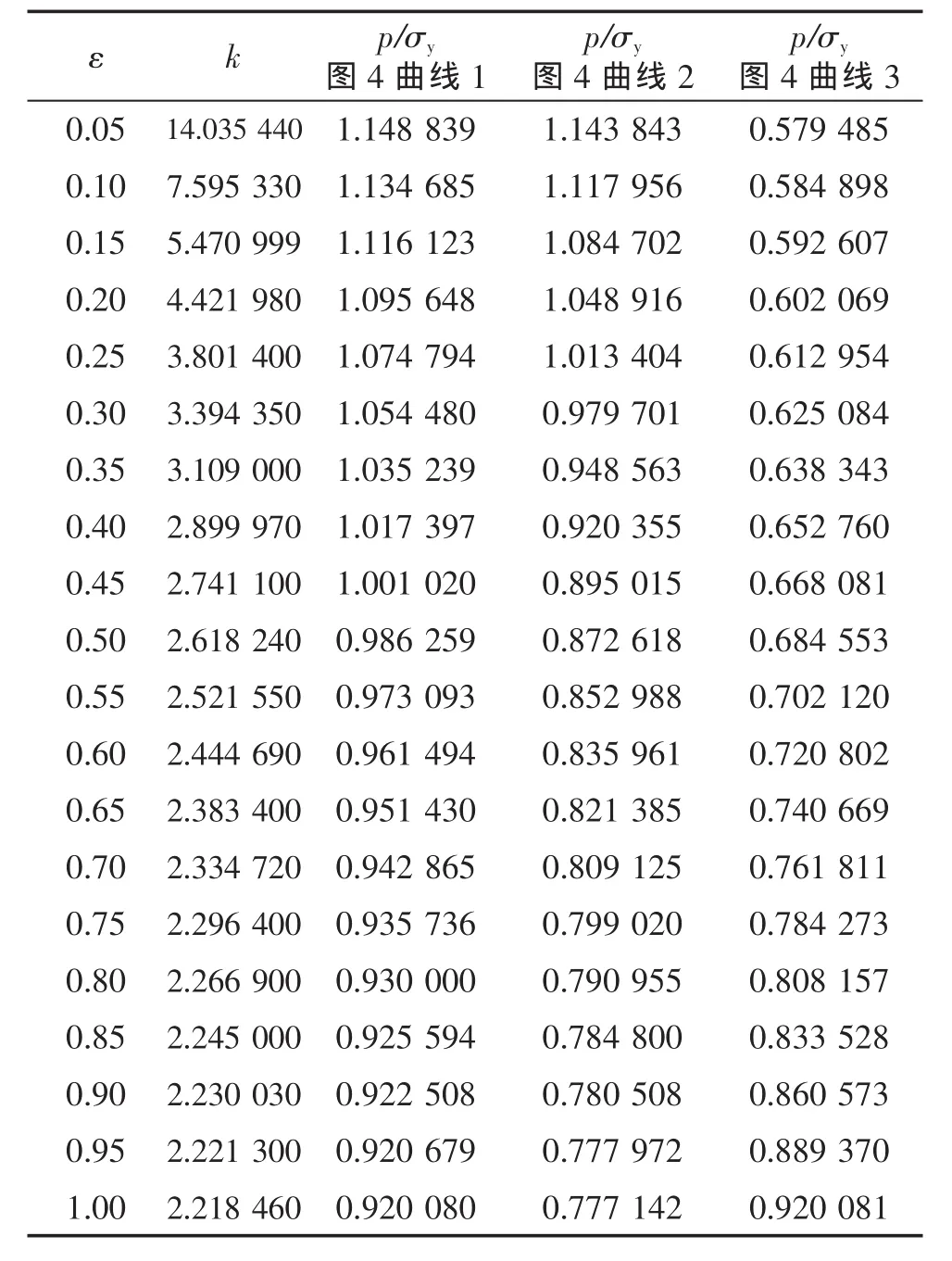
表1 ε、k和p/σy的数值关系

2 算例

下面以两个例子来验证本文的研究。例1：圆筒k=5。

按式（1），不发生反向屈服的kj=1.675 565。

按式（3），最大弹性载荷pe/σy=0.554 256。

按式（4），使rj处总应力的当量应力最小的kj=1.616 074<1.675 565，不会发生反向屈服，但限于承载能力p/σy=0.554 256。

按式（7）得承载能力p/σy=1.071 292，按式（8）得承载能力p/σy=1.108 513，二者相差0.037 221。假设σy=500 MPa，则按式（8）所得的承载能力比按式（7）的高18.610 5 MPa。

（1）kj=1.616 074（ε=15.402%）时

①按式（3），最大弹性载荷pe/σy=0.554 256，在此条件下的计算结果为:

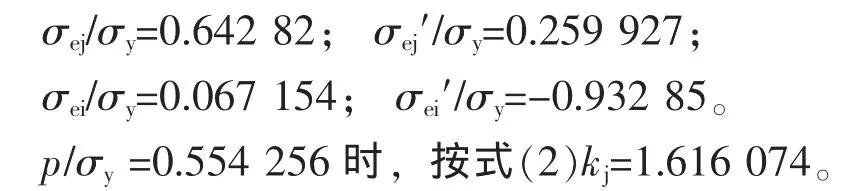
②按式（7）得承载能力p/σy=1.071 292，在此条件下的计算结果为:

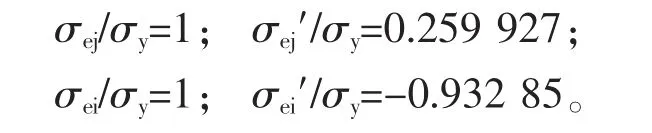
p/σy=1.071 292时，按式（2）的观点，kj=2.528 854。这时：σej/σy=0.878 782；σej′/σy=0.576 543；σei/σy=0.224 796；σei′/σy=-1.708 05。虽然σej/σy较小，但σei′远远超过压缩屈服强度，所以限制σej并不可取。

③按式（8）得承载能力p/σy=1.108 513，在此条件下的计算结果为:

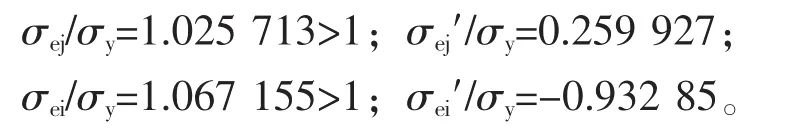
残余应力不变，因为它只取决于k和kj。如果允许σej和σei略超过屈服强度，则这一方案也是可取的。

按式（5）得承载能力p/σy=0.554 256=pe/σy。

p/σy=1.108 513时，按式（2）的观点，kj=2.611 698。这时：σej/σy=0.888 951；σej′/σy=0.595 737；σei/σy=0.242 54；σei′/σy=-1.757 46。虽然σej/σy较小，但σei′远远超过压缩屈服强度。

（2）kj=1.675 565（ε=16.889 2%）时

①按式（3），最大弹性载荷pe/σy=0.554 256，在此条件下的计算结果为:

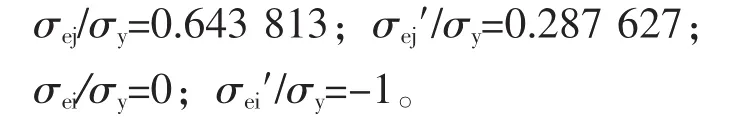
②按式（7）得承载能力p/σy=1.071 292，在此条件下的计算结果为:

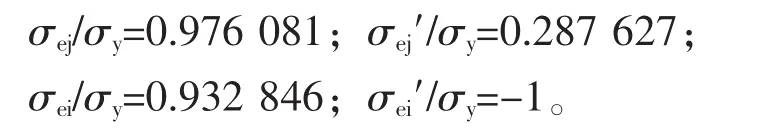
③按式（8）得承载能力p/σy=1.108 513，在此条件下的计算结果为:

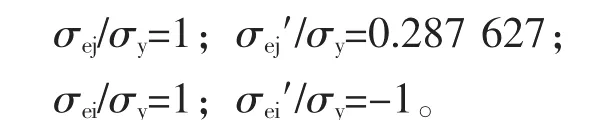
按式（5）可得承载能力p/σy=0.595 999。这时：

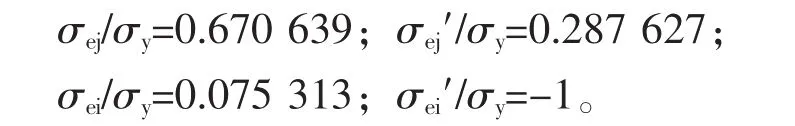
例2：圆筒k=3。

按式（1），不发生反向屈服的kj=1.748 442。

按式（3），最大弹性载荷pe/σy=0.513 2。

按式（4），使rj处总应力的当量应力最小的kj=1.559 623<1.748 442，不会发生反向屈服，但限于承载能力p/σy=0.513 2。

按式（7）得承载能力p/σy=0.934 51，按式（8）得承载能力p/σy=1.026 4，二者相差0.091 89。假设σy=500 MPa，则按式（7）所得的承载能力比按式（8）的高45.945 MPa，这个数值不小。

（1）kj=1.559 623（ε=27.981%）时

①按式（3），最大弹性载荷pe/σy=0.513 2，在此条件下的计算结果为:

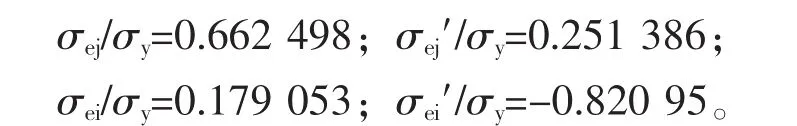
②按式（7）得承载能力p/σy=0.934 51，在此条件下的计算结果为:

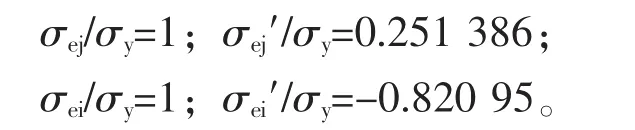
p/σy=0.934 51时，按式（2）的观点，kj=2.246 356。这时：σej/σy=0.835 237；σej′/σy=0.501 107；σei/σy=0.168 588；σei′/σy=-1.517 47。虽然σej/σy较小，但σei′远远超过压缩屈服强度。

③按式（8）得承载能力p/σy=1.026 4，在此条件下的计算结果为:

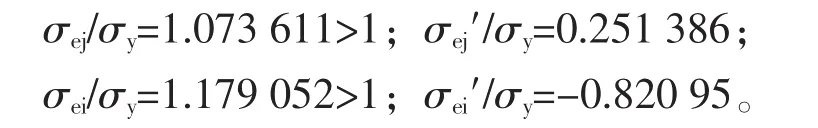
残余应力不变，因为它只取决于k和kj。σei超过屈服强度过多，这一方案不可取。

按式（5）得承载能力p/σy=0.513 2。p/σy=1.026 4时，按式（2）的观点，kj=2.432 424。这时：σej/σy=0.865 611；σej′/σy=0.552 623；σei/σy=0.204 862；σei′/σy=-1.646 99。虽然σej/σy较小，但σei′远远超过压缩屈服强度。

（2）kj=1.748 442（ε=37.422%）时

①按式（3），最大弹性载荷pe/σy=0.513 2，在此条件下的计算结果为:

②按式（7）得承载能力p/σy=0.934 51，在此条件下的计算结果为:

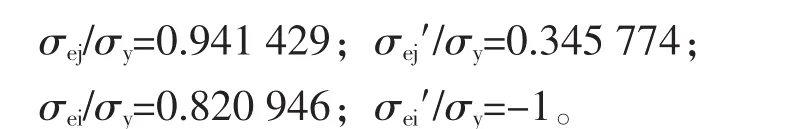
③按式（8）得承载能力p/σy=1.026 4，在此条件下的计算结果为:

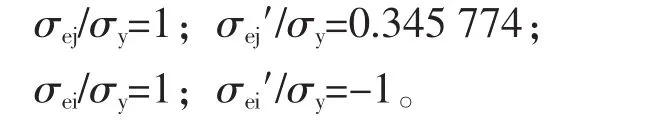
按式（5）得承载能力p/σy=0.645 16（比k=5情况下的承载能力p/σy=0.595 999还大，不合理）。这时：

3 结论

比较了不同观点下的塑性区深度和承载能力，给出了相关的计算公式和图表，通过算例验证了研究结果。再一次证明了以公式

确定塑性区深度，同时以公式

确定承载能力是最佳的，这时σej/σy=1，σej′/σy<1，σei/σy=1，σei′/σy=-1。

符号说明

ri、rj、ro——分别为圆筒的内半径、弹塑性界面半径和外半径，m

k——圆筒的外、内半径之比，k=ro/ri

kj——圆筒的弹塑性界面半径与内半径之比，kj=rj/ri

kc——临界径比，kc=2.218 457 489 916 7…

p——圆筒的内压，MPa

pe——最大弹性承载能力（初始屈服压力）,MPa

σy——屈服强度，MPa

σe——当量应力，MPa

[1] 余国琮.化工容器及设备[M].北京：化学工业出版社，1980.

[2] 陈国理.压力容器及化工设备[M].广州：华南理工大学出版社，1994.

[3] Zhu Ruilin.Ultimate load-bearing capacity of cylinder deRIVed from autofrettage under ideal condition[J].Chinese Journal of Mechanical Engineering,2008，21(5)：72-78.

[4] 朱瑞林，朱国林.外压自增强圆筒的设计计算方法[J].中国机械工程，2010，21（15）：1 869-1 874.

[5] Zhu Ruilin.Results resulting from autofrettage of cylinder[J].Chinese Journal of Mechanical Engineering,2008，21(4)：105-110.

[6] 数学手册编写组.数学手册[M].北京:高等教育出版社,1984.

Study on Depth of Plastic Zone and Load-bearing Capacity of Autofrettaged Cylinder

Zhu Ruilin Zhu Guolin

From the standpoint of limiting the equivalent stress of the total stresses at elastic-plastic juncture and the equivalent residual stresses at inside surface,depth of plastic zone and load-bearing capacity for thick wall cylinder are studied，and formulas，figures and tables are offered.

Thick wall cylinder；Autofrettage；Overstrain；Load-bearing capacity；Pressure vessel

TQ 050.1

*国家科技部创新基金资助项目（09C26214305047）。

**朱瑞林，男，1962年生，博士，教授。长沙市，410081。

2011-10-21）