厚壁圆筒自增强几个关键问题辨析*
朱瑞林 李 权
(湖南师范大学工程与设计学院)
厚壁圆筒自增强几个关键问题辨析*
朱瑞林**李权
(湖南师范大学工程与设计学院)
摘要以塑性区深度表征超应变度,研究了不同的超应变度计算方法对自增强圆筒有关应力及承载能力的影响,分析了不同的超应变度计算方法所产生的效果,提出了相关的计算公式和图表。
关键词厚壁圆筒自增强承载能力超应变度压力容器
0 前言
描绘自增强圆筒应力分布与承载能力等的参数和计算式纷繁复杂且相互密切联系,这些参数的变化往往引起自增强圆筒应力分布与承载能力等的相应变化,且牵一发而动全身。尽管实际使用的自增强圆筒的应力未必完全精确地由这些参数和公式刻画,但对于材料完全弹塑性且各向同性、不计包辛格 (Bauschinger)效应、不计应变硬化、材料没有缺陷且横截面为绝对圆形的圆筒,其应力分布与承载能力等特性理论上一定是由这些参数和计算式决定的。实际使用的自增强圆筒,其应力情况与承载能力等也必须以理论结果为基础,或者说应该采用理论研究结果并在理论基础上进行修正。
对于自增强的具体工程问题,国内外不少学者进行了一系列研究,例如,文献 [1-3]便是典型的研究,这些研究都运用了自增强技术的一般理论。本文着眼于一般的理论研究,针对上述理想情况下的圆筒,按第三强度理论进行分析计算,以便得到一般的规律。至于实际使用的自增强圆筒,不妨在此基础上加以修正。
超应变度是关键参数,故本文从超应变度出发着手研究。为方便起见,本文以塑性区深度表征超应变度。
1 超应变度的确定方法及其比较
由文献 [4-7]中关于自增强的理论结果,可以导出弹塑性界面处总应力的当量应力σejT为

式中σy——屈服限;
k——径比,即内外半径之比;
kj——塑性区深度,为塑性区半径与内半径之比,kj与超应变度ε的关系是ε=(kj-1)/k;
p——圆筒所承受的内压。
本文以p/σy表征承载能力。同时也可导出内壁面上残余应力的当量应力σei′为

有的文献 (如文献 [4,5])提供了一个确定塑性区深度的公式,其原则是使σejT最小,结果是

此时σejT/σy的最小值为

下面研究按式 (3)确定塑性区深度时,内壁面上残余应力的当量应力如何表达。为此,将式 (3) 代入式(2), 得

对式 (5),令σei′/σy≥-1,得

针对式 (6),分4种情况讨论。
(1)第一种情况:

此时,为使σei′/σy≥-1,应有

(令2.218 457 489 916 7…=kc,kc可称为临界径比)即只有当kj≤kc,亦即p/σy=lnkj≤0.796 812…时,k≥kj;kj≥kc,即 p/σy=lnkj≥0.796 812…时,k≤kj,工程上无意义。0.5≤p/σy≤0.796 812…对应于e0.5≤kj≤kc。
(2)第二种情况:

此时,为使σei′/σy≥-1,应有
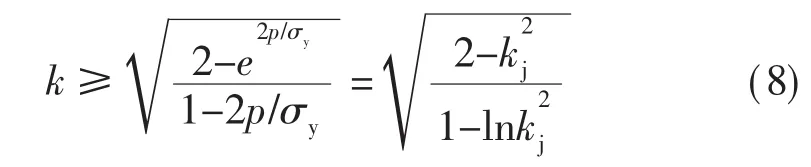
(3)第三种情况:

这种情况为不可能事件。
(4)第四种情况:
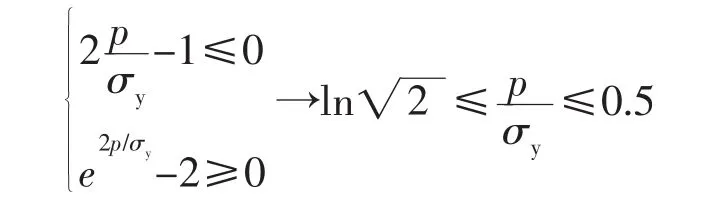
满足上式时,式 (6)必成立。即ln20.5≤p/σy≤0.5时,必有σei′/σy≥-1, 亦即按kj=ep/σy确定塑性区深度时,若ln20.5≤p/σy≤0.5,卸除自增强压力后不发生压缩屈服。ln20.5≤p/σy≤0.5对应于20.5≤kj≤e0.5。
式 (6)所表示的k~p/σy关系 (取等号)如图1中实曲线bac、df两段所示,图中虚曲线dah是kj= exp(p/σy),借此可清晰地比较k、kj的大小关系。式(6) 取等号后将 k对 p/σy求导可得:p/σy= 0.796 812…时,k有极小值kc(即图1中点a)。这一结果也可结合式 (7)、式 (8)分析而知。点a把曲线bac分成ba、ca两部分。p/σy=0.5时,k=∞。图1中ba部分的k~p/σy关系交换纵、横坐标后重绘于图2,该图同时绘出了最大弹性承载能力pe/σy、全屈服压力py/σy和 σejT/σymin,以便于分析、比较。图1中ba、ca部分实际上反映的是承载能力,承载能力的解析式就是式 (6),这是一个以k为自变量、p/σy为因变量的隐式。由图2可知,按kj=exp(p/σy)确定塑性区深度,按式 (6)确定承载能力,可使σejT/σymin远小于1, 且k越大,σejT/σymin越小。
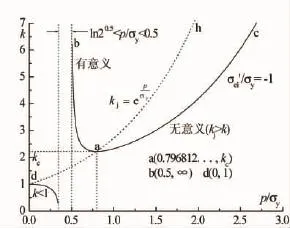
图1 曲线k22p/σy-2

图2 kj=exp(p/σy)时的承载能力与σejT/σymin
利用kj=exp(p/σy)关系可将图1中ba、ca部分所表示的k~p/σy关系转换成相应的k~kj关系,分别如图3、图4所示。
按照kj=exp(p/σy)的关系,ca部分所对应的塑性区深度有kj>k(kj在图3中直线kj=k之上),ca部分所对应的承载能力有p/σy≥lnk,这种情况在工程上无意义。而同样按照kj=exp(p/σy)的关系,ba部分所对应的塑性区深度有kj<k(kj在图4中直线kj=k以下),ba部分所对应的承载能力有p/σy≤lnk(比较图2中曲线ai、ab)。但由图 2可以看到,承载能力p/σy是随着k的增大而下降的。也就是说,若既要使σejT/σy最小,又要保证不发生压缩屈服,就只能按式(6)确定承载能力,而式(6)对应于曲线ba部分 (ca部分因kj>k而无意义)的情况表明圆筒越厚,承载能力反而越低,这不符合工程事实。导致这种现象发生实际上是由于采用了 “弹塑性界面上总应力最小”这一原则,kj=exp(p/σy)便是这一原则的结果。所以 “弹塑性界面上总应力最小”这一原则是值得商榷的。

图3 kj>k时的k~kj关系

图4 kj=exp(p/σy)时避免压缩屈服的塑性区深度

利用kj=exp(p/σy)可将式 (6)转换成
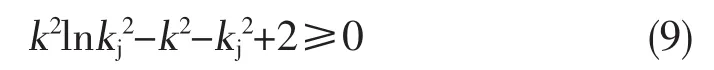
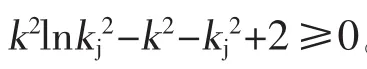

从图2看到,按kj=exp(p/σy)确定塑性区深度, 按式(6) 确定承载能力,σejT/σymin远小于 1。于是设想,若按kj=exp(p/σy)确定塑性区深度,而使σejT/σy=1,情况将如何呢?这只要把kj=ep/σy代入式 (10)即可得到

此时kj=exp(p/σy)=k,即需要作全屈服的自增强处理才能使圆筒承载后弹塑性界面总应力σejT/σy= 1。但是,全屈服状态 (kj=k)下,欲不产生压缩屈服,根据式 (9)应有
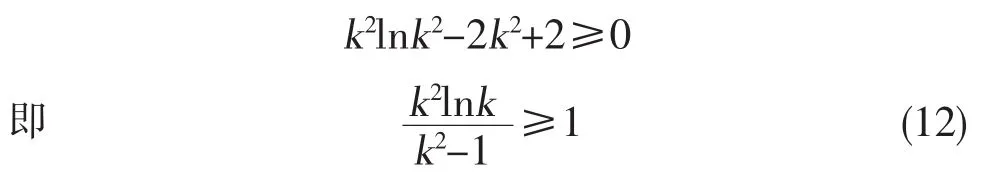
由此导出k≤kc,径比超过kc的圆筒作全屈服自增强处理时一定会发生压缩屈服;径比小于kc的圆筒作全屈服自增强处理后其承载能力可达到全屈服压力。
即使不考虑kj=exp(p/σy)的关系,也可以证明当p/σy=lnk时,为使σejT/σy=1,也须有kj=k。为此将p/σy=lnk代入式 (10),整理后得

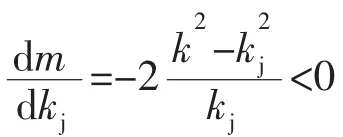
将p与pe作比较,可清楚地看出自增强的效果,为此令

将式 (6)取等号,利用式 (14)将p/σy另换算成n,把式 (6)的结果列于表1,并将n~k关系绘于图5,以备工程上查用。

表1 k与p/σy的数值关系(0.5≤p/σy≤0.796 812…)(σei′/σy=-1,σejT/σy最小)
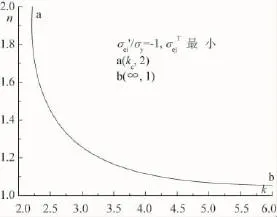
图5 使σejT/σy最小、σei′/σy=-1的n~k关系
下面比较总应力的分布情况。以k=3为例,不发生压缩屈服时,kj=1.748 442。按照文献 [6]的观点,这样的圆筒可承载p=2pe=(8/9)σy,图6(a)是这种情况下的总应力分布。按照kj=exp(p/σy)的观点,这样的圆筒可承载p=lnkj=0.558 725…σy。图6(b)是这种情况下的总应力分布。若不考虑压缩屈服问题,承受p=2pe=(8/9)σy的载荷时,按照kj=exp(p/σy)的观点,kj=2.432 425…,总应力分布如图6(c)所示。kj=1.748 442、p=0.8σy的总应力分布如图6(d)所示。有关参数标注在相应的图中,图中x代表筒壁中点的相对位置,即点的半径与内半径之比。
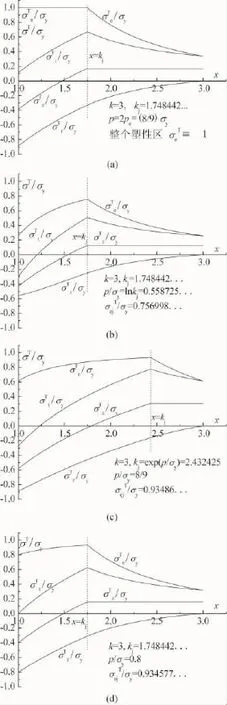
图6 总应力分布的比较
由图6看到,由于其中图(a)、(c)、(d)三种情况下圆筒受载较大,故应力水平较高,但在安全范围内;而图(b)情况下圆筒受载较小,故应力水平较低。在图(a)情况下,由于kj由式(9)确定且p=2pe,故整个塑性区总应力的当量应力σeT/σy≡1。在图(d)情况下,kj由式 (9)确定,载荷比 2pe略小,因而σeT/σy从内壁面略小于1开始缓慢上升至弹塑性界面处等于 1。值得注意的是,要承受 p= 0.558 725…σy的载荷,按照文献 [6]的观点,即p/σy=(k2-1)/k2=0.558 725,从而 k=1.505 377…<kc。由于当k<kc时,(k2-1)/k2>lnk,按p/σy=(k2-1)/k2承载会使 σejT/σy>1, 由此只能按 p/σy=lnk承载,但ln1.505 377…<0.558 725…,故要承受p= 0.558 725…σy的载荷,可利用k=kj=1.748 442的圆筒作全屈服自增强处理,既不会发生压缩屈服,也可承载p/σy=lnk=0.558 725…的载荷。事实上,表1中对所有k都有kj<kc,为承受表1第2栏的载荷,不必使用第1栏的径比,而只需使用径比k=kj的圆筒作全屈服自增强处理即可。例如,为承受p/ σy=0.538 103的载荷,不必使用k=3.5的圆筒,而只需使用k=1.712 755的圆筒。对该圆筒作全屈服自增强处理,即可承受p/σy=0.538 103的载荷。这样,厚度可降低,即
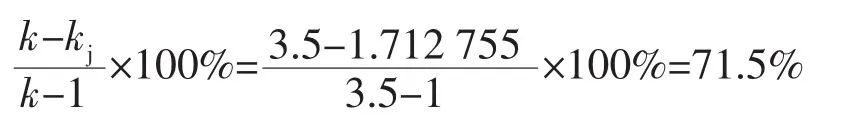
对于p/σy≤0.796 812的载荷,都可以采用全屈服自增强处理的圆筒,使其承受p/σy=lnk载荷。至于p/σy>0.796 812的载荷,若以kj=exp(p/σy)确定塑性区深度,会发生反向屈服,见下述的算例。
2 算例验证
例1,k=3。
①按式(9),不发生反向屈服的kj=1.748 442,承载能力为p/σy=2pe/σy=0.889。按式(1),σejT/σy= 1; 按式(2), σei′/σy=-1。
② p/σy=0.889(>0.796 812) 时, 按式(3),kj=2.432。 kj=2.432时, 按式(1), σejT/σy=0.935;按式 (2),σei′/σy=-1.385 (压缩屈服)。
③为了不发生压缩屈服,由k=3查表1得p/σy=0.558 725。此时,按式(3),kj=1.748 442,与上述第①种情况相同;按式 (1),σejT/σy=0.757;按式 (2),σei′/σy=-1 (不发生压缩屈服)。
例2,k=5。
①按式(9),不发生反向屈服的kj=1.675 565,承载能力为p/σy=2pe/σy=0.96。按式 (1),σejT/σy=1;按式 (2),σei′/σy=-1。
②p/σy=0.96时,按式(3),kj=2.612,kj=2.612时,按式(1), σejT/σy=0.889;按式(2),σei′/σy= -1.757(压缩屈服)。
③为了不发生压缩屈服,由k=5查表 1得p/σy=0.516 15。此时,按式 (3),kj=1.675 565,与上述第①种情况相同; 按式(1), σejT/σy=0.671;按式 (2),σei′/σy=-1(不发生压缩屈服)。
3 结论
本文以塑性区深度表征超应变度,研究了不同的超应变度计算方法对自增强圆筒有关应力及承载能力的影响,分析了不同的超应变度计算方法所产生的效果,提出了相关的计算公式和图表。因此,有下面的结论:
(1)按 kj=ep/σy确定塑性区深度, 可使弹塑性界面处总应力的当量压力最小,且远小于屈服限;为使内壁面残余应力的当量压力不超过屈服限 (不发生压缩屈服),相应于按kj=ep/σy确定塑性区深度的承载能力须随着径比的增加而降低,弹塑性界面处总应力的当量压力小于屈服限,若使弹塑性界面处总应力的当量压力等于屈服限,承载能力可达到全屈服载荷,但仅限于径比k≤2.218 457 489 916 7…的圆筒。
(2)按k2lnkj2-k2-kj2+2≥0确定塑性区深度时,内壁面残余应力的当量压力等于屈服限,若同时使弹塑性界面处总应力的当量压力等于屈服限,径比k≤2.218 457 489 916 7…时,承载能力为全屈服载荷;径比k≥2.218 457 489 916 7…时,承载能力为最大弹性承载能力的2倍。
(3)不论从什么角度控制内壁面残余应力的当量压力不超过屈服限,结果都得到k2lnkj2-k2-kj2+ 2≥0。例如,按kj=ep/σy确定塑性区深度,保证内壁面残余应力的当量压力不超过屈服限的结果也相当于k2lnkj2-k2-kj2+2≥0。
(4)塑性区深度kj≤e0.5时,不论径比多大,都不会发生压缩屈服。按不发生压缩屈服的观点,此时p/σy≤0.5。
参考文献
[1]Xiaotao Zheng,Fuzhen Xuan.Autofrettage and shakedown analysis of strain -hardening cylinders under thermo -mechanical loadings [J ].JournalofStrainAnalysis Engineering and Design,2011,46(1):45-55.
[2]Rees D W A.Autofrettage of thick-walled pipe bends[J]. International Journal of Mechanical Sciences, 2004, 46 (11):1675-1696.
[3]郑小涛,轩福贞.热-机载荷下厚壁圆筒自增强压力与安全性分析 [J].机械工程学报,2010,46(16):156-161.
[4]余国琮.化工容器及设备 [M].北京:化学工业出版社,1980.
[5]陈国理.压力容器及化工设备 [M].广州:华南理工大学出版社,1994.
[6]Zhu Ruilin.Ultimate load-bearing capacity of cylinder derived from autofrettage under ideal condition[J]. Chinese Journal of Mechanical Engineering,2008,21(5):72-78.
[7]王志文.化工容器设计 [M].北京:化学工业出版社,1990.
埃克森美孚授权转让远程天然气泄漏检测技术
埃克森美孚授权为加工装置转让远程天然气泄漏检测技术。埃克森美孚石油公司上游研究公司于2014年2月20日将其创新的InteliRed远程气体探测系统提供给共同开发者普罗维登斯光子学(Providence Photonics)公司授予第一个商业许可。
该 InteliRed系统旨在提高炼油厂、化工厂、LNG设施和其他气体处理设施过程的安全和环保性能。这个新的先进的系统采用了一个专门开发的计算机算法,可自动分析红外摄像机图像,以便检测逃逸的烃类气体。该InteliRed系统可提供烃类泄漏的早期预警警报,实现最小的假警报。
普罗维登斯光子学公司是普罗维登斯工程公司的附属公司,总部位于美国巴吞鲁日。埃克森美孚和普罗维登斯的科学家化了4年时间共同开发了InteliRed系统,还积累了该系统自2013年至今在卡塔尔的液化装置上的实地测试经验。(钱松)
*湖南省教育厅重点资助科研项目,编号12A087。
**朱瑞林,男,1962年生,博士,教授。长沙市,410081。
中图分类号TH49
(收稿日期:2013-10-15)
Discrimination between Key Problems on Autofrettage of Thick Wall Cylinder
Zhu Ruilin Li Quan
Abstract:Characterizing overstrain with the depth of plastic zone,studied the influence of different overstrain calculation methods on stress and bearing capacity of autofrettaged cylinder.Analyzed the effect of different methods for overstrain calculation,offered the relevant formulas and charts.
Key words:Thick wall cylinder;Autofrettage;Load-bearing capacity;Overstrain;Pressure vessel

