无控制点条件下的SAR影像直接定位

2012-12-11 06:08张笑微

测绘通报 2012年1期

张笑微，姜挺，王鑫，张锐，张一

(信息工程大学地理空间信息学院，河南郑州450052)

一、引言

合成孔径雷达(SAR)具有全天时全天候成像、不受云雾干扰等特点，在军事侦察、地质勘探、灾害预防、环境监测等领域发挥着重要作用[1]。然而自诞生之日起，SAR影像的目视判读特性和几何特性均不甚理想，不便于进行大规模地形测绘。究其原因，既有SAR成像过程复杂、受干扰多等客观因素，也有在SAR影像上人工选取控制点的偶然误差大等主观因素。随着卫星制造技术及其他相关技术的不断发展，SAR影像的几何分辨率不断提高，已经达到米级，遥感器的轨道参数也越来越精确，使得SAR影像也可以用于测制地形图和目标定位[2]。在我国，虽然已经开展“西部测图”计划，但仍有相当面积的国土地形图还未进行测制，这些地区或人迹罕至，或常年云雾覆盖，处于光学遥感卫星覆盖的盲区，且普遍缺乏地面控制点。研究无控制条件下的SAR影像直接定位，对于填补我国部分地区的测图空白具有一定的指导意义。

要实现SAR影像的无控制点直接定位，精确的成像几何模型必不可少。几十年来，国内外学者先后提出了多种SAR成像几何模型。这些模型包括苏联的顿斯科夫模型，1988年ISPRS大会上提出的Konecny 模型[3]，以及 Curlander提出的距离-多普勒(R-D)模型[4]。其中，顿斯科夫模型在理论上是严密的，但形式过于复杂，不适于进行工程应用和计算;Konecny模型类似于光学遥感中的共线条件方程，建立了实际地面与图像的对应关系。尽管考虑了地形起伏和成像关系，但Konecny模型仍然将成像几何处理为中心投影，而SAR则是距离投影成像，从严格意义上讲，Konecny模型只是对SAR成像的近似表达;R-D模型则从SAR成像原理出发，根据像点的距离条件和构像瞬间的多普勒条件表达图像的几何模型。综上所述，R-D模型最符合SAR成像的实际情况，在卫星星历参数较为精确的情况下，定位精度较Konecny高。

国内外已有多位学者利用R-D模型实现了SAR影像的直接定位：Curlander发展了R-D模型用于SAR定位，并分析了影响定位精度的因素;袁孝康推导出了R-D模型目标定位的解析解[5];周金萍则提出了R-D模型的相对定位法[6];陈尔学提出了解析法和数值法相结合的定位方法，在布设1个控制点的条件下，丘陵地区可取得25 m左右的精度[7]。尽管针对R-D模型的研究已经较多，但大多数研究是基于星历数据和控制点评价影像的定位精度或进行几何纠正，鲜有无控制条件下直接定位的研究和试验。下文中，笔者将利用R-D模型和地球椭球模型，结合卫星附带的星历数据，实现SAR影像的无控制定位。

二、基于R-D模型的无控制点直接定位原理

R-D模型是确立卫星天线、影像像点和地面物点的空间几何关系，涉及的坐标系包括地心坐标系，图像坐标系和像空间坐标系。鉴于目前绝大多数商业SAR卫星的轨道参数均在WGS-84坐标系即地固坐标系(ECR)中定义，故选取ECR作为地心系，避免坐标转换产生的误差。坐标定义如图1所示。

图1中，O-XYZ即为WGS-84坐标系;S表示卫星位置;S'表示星下点;目标点为T;T'为其地面投影点;ON为地球自转轴。设目标点T的经纬度坐标为(L，B)，目标点在SAR影像上某像元坐标为(i，j)，则由以下3个方程实现无控制条件下的目标直接定位。

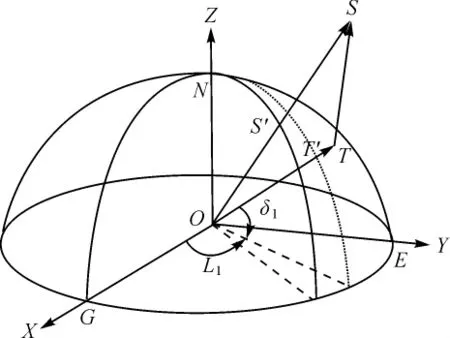
图1 用于R-D模型定位的ECR坐标系统

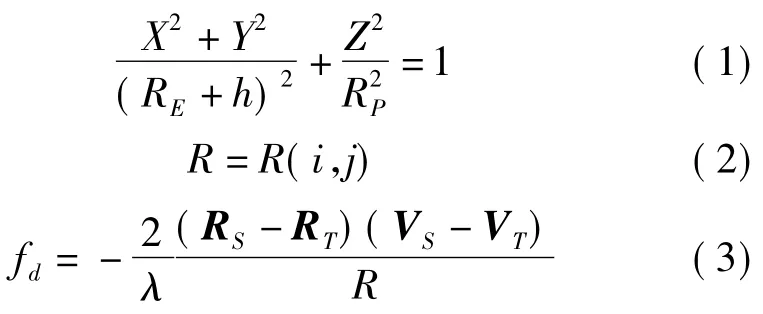
式(1)为地球椭球方程，其中RE和RP分别为椭球的长半轴和短半轴，h为目标点的高程，(X，Y，Z)表示目标点的位置坐标，记为矢量RT。

式(2)为距离向方程，R表示卫星到目标点之间的斜距，设 RS表示卫星的位置矢量，则 R=是影像列号j的函数。在卫星附带的星历数据中，提供了距离向第1个像元的扫描延迟时间T0和距离向的像元间隔y，根据T0可求出第1个像元的扫描延迟 R0=cT0/2(c表示光速)，则式(2)等价于

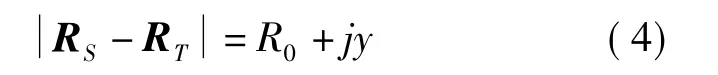
式(3)为多普勒方程，其中λ为雷达波长，VS、VT分别表示卫星和目标点的速度矢量，在ECR坐标系统中，VT=[0 0 0]T。商业卫星提供的SLC和GEC级别的影像，其多普勒中心频率均经过零化处理，故式(3)等式左端为0，等价于

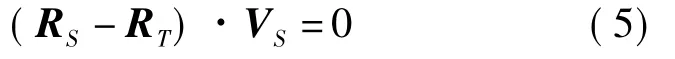
以上3式构成了一个完整的直接定位体系。若已知SAR影像上某点的像元坐标(i，j)，则可以求出对应的 WGS-84 坐标 (X，Y，Z)。

三、R-D模型的解算

R-D模型的求解有多种方法，袁孝康推导出了R-D模型的解析解，但由于解析解将地球看做具有本体半径的球体，所以求解精度受到限制。若将地球视为真正椭球体，只有通过数值迭代法才能求出最终解。数值法也有多种方法，最常见的有最小二乘迭代和牛顿-辛普森迭代。本文选取前者作为计算方法。

在一景SAR影像中，方位向每行对应不同的卫星位置和速度矢量，表示为成像时间t的函数。一般的SAR卫星会提供一组时间间隔一定的位置向量和速度向量，具体到图像上某像元成像时的轨道参数，通过对轨道向量进行处理得到。常用的处理方法有多项式内插法，拉格朗日内插法和轨道根数法，众多学者的研究表明，在轨道参数精度较高的情况下，简单的多项式内插即可达到令人满意的效果[8]。

多项式阶数的确定由控制点数量决定[9]，在没有控制点的情况下，选取三次多项式对卫星位置坐标进行拟合

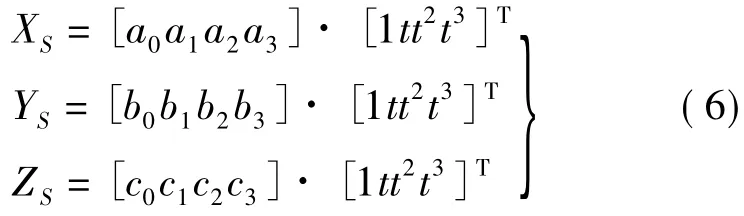
相应的速度为

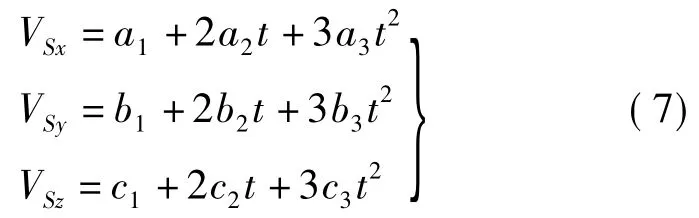
参数 ai、bi、ci(i=0，1，2，3)通过拟合计算得到。

由式(1)，式(4)，式(5)建立观测方程如下

将观测方程进行泰勒展开至一次项，此时需要给定初值h，h的选取可在影像的高程起伏范围之内，一般选取为影像中心点高程或影像覆盖区域内的平均高程，此处选取为影响覆盖区域内平均高程。则相应的误差方程为

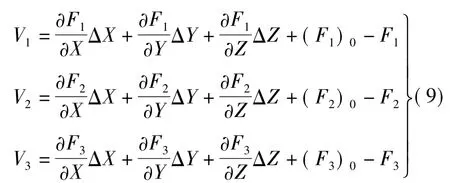
写为矩阵形式

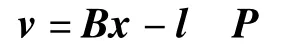
式中，v为观测值改正数向量;B为系数阵;x为地面坐标改正数向量。由最小二乘法

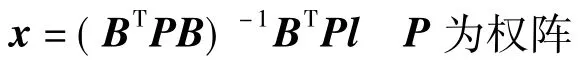
综合以上步骤，可写出求解流程为：

1)根据影像4个角点和中心点坐标，给定像点的初始高程值h;

2)计算像点对应的成像时刻t;

3)将轨道参数与成像时刻的关系表示为三次多项式，根据卫星星历表中的轨道参数，拟合得到多项式系数 ai、bi、ci;

4)误差方程线性化，根据最小二乘法迭代计算地面坐标的改正数向量x至收敛。

四、试验与分析

本文所用试验数据为TerraSAR卫星以Stritmap模式获取的武汉地区一景影像，影像大小为30 056像素×19 504像素，获取时间为2008年4月18日，获取方式为右视、升轨;方位向分辨率3m，距离向分辨率2．43m;影像覆盖区域的平均高程为371m;星历表提供了间隔为10．0 s共12组位置矢量和速度矢量。根据上文中推导的解算步骤，对影像4个角点和中心点的进行直接定位，并与提供的坐标进行对比，分别得出方位向和距离向的RMSE如表1所示。

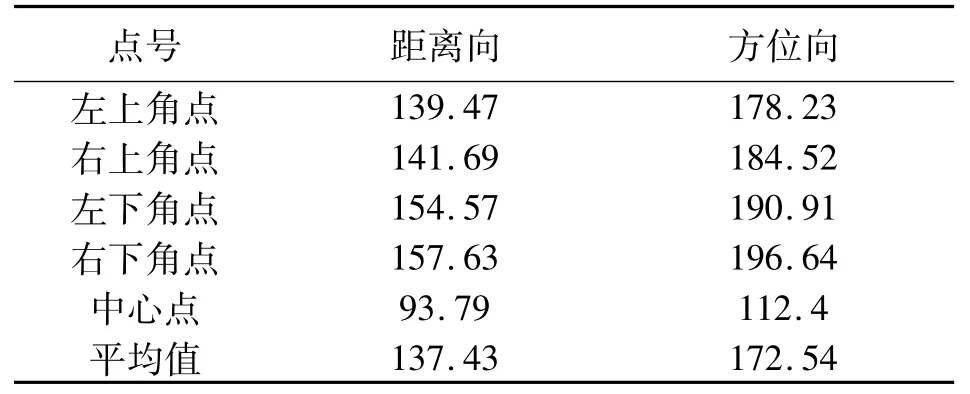
表1 方位向和距离向的RMSE m

从试验结果可以看出，由于在方位向上存在卫星位置测量这一较大的系统误差，方位向定位的中误差要大于距离向，加之地球椭球岁差、章动产生的系统误差，使得两个方向上定位的中误差均达到百米级别，显然结果并不能令人满意。

五、结束语

本文利用R-D模型，结合星历数据，实现了单景TerraSAR影像的无控制直接定位，方位向和距离向精度分别可以达到±107．43m和±172．54m，证明了该理论的可行性。虽然试验精度并不令人满意，但鉴于全球覆盖覆盖范围内的30m精度级别的DEM已经可以公开获取，因此可基于DEM进行影像模拟和匹配，设置“伪控制点”消除系统误差，以精化定位结果;也可以由Google Earth上选取精度不高的控制点改善定位精度。由于本文试验数据有限，上述结论和其他可能改善定位结果的假设还需要更多的试验进行验证。

[1]靳国旺．InSAR获取高精度DEM关键处理技术研究[D]．郑州：信息工程大学，2007．

[2]杨杰．星载SAR影像定位和从星载InSAR影像自动提取高程信息的研究[D]．武汉：武汉大学，2004．

[3]肖国超，朱彩英．雷达摄影测量[M]．北京：地震出版社，2001．

[4]CURLANDER J．Location of pixels in spacebome SAR imagery[J]．IEEE Transaction on Geoscience and Remote Sensing，1982，20(3)：359-364．

[5]袁孝康．星载合成孔径雷达导论[M]．北京：国防工业出版社，2003．

[6]周金萍．星载SAR图象的实用化R-D定位模型[D]．北京：中国科学院研究生院，2000．

[7]陈尔学．星载合成孔径雷达正射校正方法研究[D]．北京：中国林业科学研究院，2004．

[8]袁修孝，吴颖丹．缺少控制点的星载SAR遥感影像对地目标定位[J]．武汉大学学报：信息科学版，2010，35(1)：88-94．

[9]张过．缺少控制点的卫星遥感影像精纠正[D]．武汉：武汉大学，2005．