高速铁路坐标系衔接的相关问题探讨

梁 永

(铁道第三勘察设计院集团有限公司，天津300251)

一、引 言

高速铁路工程测量规范中规定：在线路轨面设计高程面上坐标系统的投影长度变形值不大于10mm/km，且高速铁路无砟轨道平顺性要求测量精度高。规范要求CPⅠ控制网相邻点的相对点位误差小于±10mm，CPⅡ控制网相邻点相对点位中误差小于±8mm，CPⅢ控制网精度要求小于±1 mm。铁路是典型的线性工程，穿行于狭长的带状区域，在坐标投影的过程中，长度发生了很大的变形，使得图上距离与实地距离有较大差异，尤其在带边缘变形更大。为了满足施工精度要求，就必须重新进行施工坐标系设计，但往往由于相邻坐标系变形程度不一样，在相邻的两个坐标系的边缘利用相同的控制点放样同一个中线点而不在同一个位置，属于同基准下坐标系间衔接问题;另外一种情况是不同的工程项目由于各自采用的坐标系统不一样，线路在接轨时需要进行坐标系衔接，属于不同基准间坐标系的衔接问题。本文重点对相同基准和不同基准下坐标系衔接问题进行探讨。

二、同基准下坐标系衔接问题探讨

1．长度投影变形分析

1)将地面观测值规划到参考椭球面上，其长度变形由下式计算

式中，S为地面测量距离;Hm为高出参考椭球面的平均高程;RA为地面边方向参考椭球面法截弧曲率半径。

ΔS1为负值，表明地面实测长度归算到参考椭球面总是变短的，且变形值与归算边高出参考椭球面的平均高程成正比。

2)将参考椭球面上边长改化至高斯平面上，其长度变形由下式计算

式中，S为地面测量距离;ym为地面边两端点近似横坐标平均值;Rm为参考椭球面在地面边中点的平均曲率半径。

ΔS2为正值，表明将参考椭球面上的长度投影到高斯平面上总是变长，而且变形值与横坐标平方成正比，即投影变长离中央子午线越远，变形越大。

3)综合以上分析，距离观测值从地面投影的高斯平面总的长度变形为

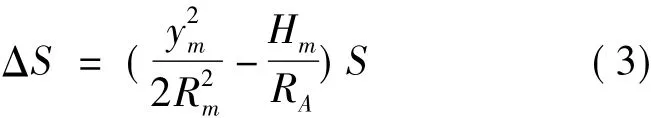
从式(3)可知，高程归化改正值一般为负值，高斯投影改正值为正值，通过选择合适得中央子午线和投影面进行抵偿，可以减小长度变形，即建立抵偿施工坐标系。

2．施工坐标系设计

以某客专工程施工坐标系设计为例说明。

椭球参数：WGS-84椭球。投影方式：标准3°带正形投影。中央子午线：117°。

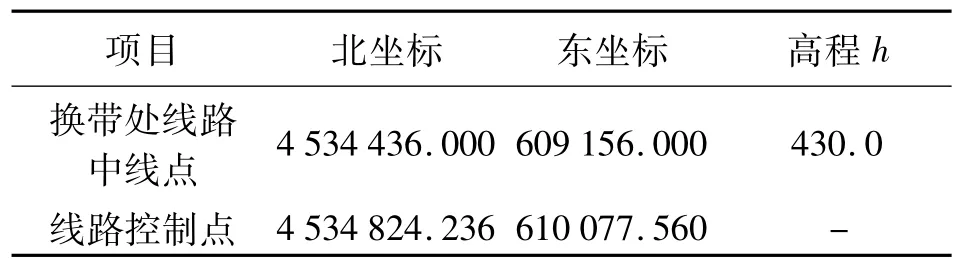
表1 某客专工程施工坐标系设计 m

按照式(3)计算，线路换带处投影变形为79mm/km，很明显不满足高速铁路最大变形量10mm/km的精度要求，因此需建立工程独立坐标系。坐标系设计参数如下。

第1施工坐标系：中央子午线精度L=118°15'，投影面大地高H=420m。

第2施工坐标系：中央子午线精度L=118°0'，投影面大地高H=445m。

仍然按式(3)进行计算分析，换带处在第1施工坐标系投影变形为-2 mm/km，在第2施工坐标系投影变形为9mm/km。因此，新设计的两个工程独立坐标系是满足高速铁路最大变形量10 mm/km的精度要求的。

同时还发现，新设计的两个坐标系下各自的变形量虽然都满足规范10mm/km的变形要求，但其在换带处变形是不一样的，其变形量之差绝对值为11mm/km。按照上述分析，如果利用相同的控制点进行中线放样，在两个坐标系所放样的同一个点必然会有11mm的误差(不考虑测量误差)，这样仍然不满足CPⅢ测量搭接精度和线路平顺性的要求，在换带处线路平面坐标发生突变，解决该问题的唯一方法是在轨道精调时，通过施工现场进行平顺处理。

3．施工坐标系的坐标计算

施工坐标系坐标计算的数学模型有：椭球平移法、椭球膨胀法、布尔沙模型法等。

以常用的椭球膨胀法为例，基本原理是将原来基准下的三维直角坐标在新的椭球基准下进行投影，得到新椭球坐标系指定高程面下的坐标，但其椭球的扁率及定位和定向不变。

新椭球半径

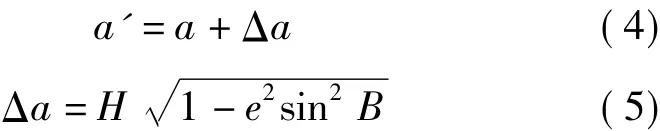
仍以上述项目为例，进行施工坐标系坐标计算，结果如下。

表2 第1施工坐标系计算结果 m

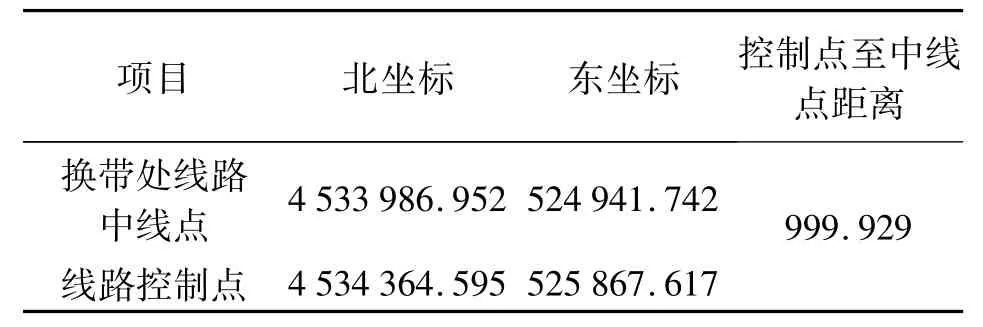
表3 第2施工坐标系计算结果 m

通过上述两个表比较：在两个坐标系利用同样的控制点进行换带处中线点放样，有10 mm的差值，与坐标系设计分析的结果(11mm)是一致的。

由此分析，即使每个坐标系设计均满足规范10mm/km的情况下，但在换带处由坐标系设计而引起的坐标差最大可达20 mm/km，因此进行坐标系设计时，在换带处对投影变形必须给予控制和约束。

4．坐标系设计在换带处控制约束

通过上述分析，由坐标系设计在换带处引起的误差直接导致中线点的放样误差，如果对此问题考虑不足，会给工程施工带来很大的不便，因此必须采取一定的措施，减小由于坐标设计而引起的测量误差。

从实例中发现，设计的两个坐标系的变形值虽然都满足规范10 mm/km的变形要求，但其变形程度是不一致的，而且一正一负。那么，在坐标系设计时通过计算，选择合适的中央子午线和投影面大地高，在换带边缘使其中线长度变形量差值的绝对值宜控制在5mm/km以内。

以某客专项目为例说明。

椭球参数：WGS-84椭球。投影方式：标准3°带正形投影。中央子午线：126°。

表4 某客专项目坐标 m

按照式(3)计算，换带处投影变形为-18．4mm/km，很明显不满足高速铁路最大变形量10mm/km的精度要求，因此需建立工程独立坐标系。坐标系设计参数如下。

第1施工坐标系：中央子午线精度L=126°12'，投影面大地高H=90m。

第2施工坐标系：中央子午线精度L=125°18'，投影面大地高H=105m。

按照式(3)进行计算分析，换带处在第1施工坐标系投影变形为6mm/km，在第2施工坐标系投影变形为7．0mm/km。因此，新设计的两个工程独立坐标系既满足规范中高速铁路最大变形量10mm/km的精度要求，同时在换带处线路中线长度变形量差值绝对值也只有1mm/km的变形。

按照以上所述的数学模型进行坐标转换计算，坐标结果如下。

表5 第1施工坐标系计算结果(换带处控制约束)m

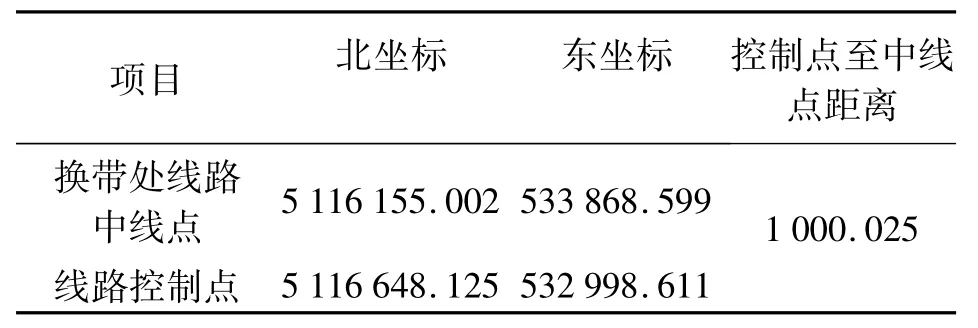
表6 第2施工坐标系计算结果(换带处控制约束)m

通过上述两个表比较：实例中新设计的两个坐标系的变形值不仅都满足规范10mm/km的变形要求，而且其变形是一致的。在两个坐标系利用同样的控制点进行换带处中线点放样，仅有1 mm的距离误差，与坐标系设计分析的结果一致，说明在坐标系设计时充分考虑这些因素，其问题是可以解决的。

三、不同基准线坐标系衔接问题探讨

1．不同基准下坐标系衔接

这种情况往往是建设的项目不同步施工，其坐标系基准和施工坐标系的投影参数也不一样。知道无砟轨道接轨处的道岔中心位置是唯一的，这就要求后期建设的项目必须在该位置准确接轨，同时还需满足高铁线路平顺性的要求。

不同基准间坐标转换常用方法有4参数法和7参数法。设计期间，如果两个项目还没有施工，只能从理论上利用项目公共的控制点，采用4参数法或7参数法进行线路坐标转换以达到不同线路间的衔接目的，但由于该方法数学模型存在不严密性(利用不同的公共控制点进行坐标转换的结果是不一样的)，工程建设不同步，前期客专施工过程中由于测量仪器、施测方法、现场施工、轨道精调及其他误差等方面原因，造成控制网绝对点位中误差的存在，轨道精调时未能调到理论中线位置，从而导致放在实地上的中线与理论上存在一定的偏差。

2．不同基准下坐标系衔接处理

综上述原因，前期设计时采用不同基准间坐标转换的方式进行线路衔接，但在后期施工期间，由于施工和测量等误差的影响，后建设的项目往往不可能与先前建设的项目顺利衔接，在线路衔接处会发生一定的偏差，不满足线路平顺性的要求。其具体处理措施是：为了确保无砟轨道顺利衔接，在线上无砟轨道施工前，首先应测设衔接处的CPⅢ测量控制网，在CPⅢ控制点测设完成后，利用轨检小车测量既有无砟轨道的岔区和直线股的中心坐标，并评价是否满足线路设计要求，如不满足要求需根据实测中线坐标进行无砟轨道中线调整，对衔接处的线路中线重新设计，然后根据重新设计线路资料进行施工，以满足相邻工程衔接精度和轨道平顺性的要求。

四、结束语

1)在同基准下坐标系衔接问题是可以通过施工坐标系设计解决的，在施工坐标系设计时采取一定的措施可以满足CPⅢ测量搭接精度的要求，避免在换带处发生线路平面坐标的突变，保证线路的平顺性;

2)采用抵偿坐标系原理进行施工坐标系设计时，考虑相邻坐标系在投影带边缘使其长度变形量尽可能一致，变形量差值的绝对值宜控制在5mm/km以内，更适合于CPIII搭接精度要求;

3)研究采用斜轴墨卡托投影方式进行坐标系设计，减少坐标系换带个数从而来减少由于相邻坐标系间投影变形不一样而导致的误差;

4)不同基准下坐标系衔接问题，宜通过外业测量既有无砟轨道的岔区和直线股的现状，并对现状进行合理评价，必要时重新进行线路中线设计以达到线路平顺性的要求。

[1]中华人民共和国铁道部．高速铁路工程测量规范(TB10601—2009)[S]．北京：中国铁道出版社，2009．

[2]孔详元，郭标明，刘宗泉．大地测量学基础[M]．武汉：武汉大学出版社，2001．

[3]黄劲松．GPS测量与数据处理[M]．武汉：武汉大学出版社，2003．

[4]梁永．高速铁路测量建立独立坐标系的数学模型[J]．铁道工程学报，2006(7)：34-36．

[5]梅熙．高斯投影变形对高速铁路线路设计的影响[C]∥高速铁路精密测量理论及测绘新技术应用国际学术研讨会论文集．成都：西南交通大学出版社，2010．

[6]张江．坐标转换在铁路勘察设计中的应用探讨[J]．铁道勘察，2010(4)：11-13．