利用一个已知点进行平面控制测量在某机场工程测量中的尝试

项 伟，李 锋，王 岩

(1．空军工程设计研究局勘测大队，北京100076;2．沈阳建筑大学土木工程学院辽宁，沈阳110168)

一、引 言

GPS定位技术的高自动化和高精度，使其在工程测量中得以广泛应用。但由于GPS观测量的结果属于地心WGS-84坐标系，地面大地测量得到的成果属于参心坐标系，两类坐标不仅坐标原点不一致，而且相应的各坐标轴之间不平行，所以在实际应用中，必须进行坐标转换[1]。由于采用的椭球不一样，并且由于投影的局限性，使得各区域存在不一致的转换参数，常用的方法是采用GPS联测两个或者两个以上参心坐标已知的点，再通过GPS解算软件进行平差，并进行投影转换，求得待定点的参心坐标。

二、某机场工程测量概况

测区呈东西走向，长度约 2300 m，宽度约350m，地势较平坦，测区面积约0．8 km2。测量内容包括地形图测量、净空测量、复测原有跑道中线真、磁方位角和跑道中心点、两端点的经纬度。测量成果应符合有关国家、军队及行业标准对详勘的要求。由于涉及征地及机场定位，应提供城市坐标系(或1980西安坐标系)和WGS-84坐标。

三、资料收集情况与方案制定

1．资料收集情况

收集到该地区5个D级GPS控制点，其成果包括WGS-84坐标和1980西安坐标。采用上述资料作为项目选点、用以制定观测计划、解算用。

2．存在的问题

由于该地区城市控制点大多埋设在冻土层以下，埋设地点多选在农田区，给找点工作带来难度。经过实地踏勘，仅找到1个D级GPS控制点(简称为MaT)。按照原有方案，不符合相应规范中“卫星定位测量控制网首级网布设时，宜联测两个以上高等级国家控制点或地方坐标系的高等级控制点”[2]规定的要求，使常规方案无法实施。

3．方案的制定

根据收集到的控制点资料的情况，5个D级GPS控制点分布于测区四周，D级GPS控制点MaT离测区最近点JP02的距离为2．7 km。点位分布情况如图1所示。

图1

针对此种情况，拟采用快速静态测量模式，如图2所示，在测区中部选择一个基准站，另一台接收机到各待定点流动设站，每点观测数分钟，得到各待定点与MaT的单基线，求得各流动站的WGS-84地心坐标。建立坐标转换模型，计算转换参数，将得到的WGS-84坐标转换成需要的1980西安坐标系统下的坐标。该方案实施的关键在于转换模型的建立和转换参数的计算。

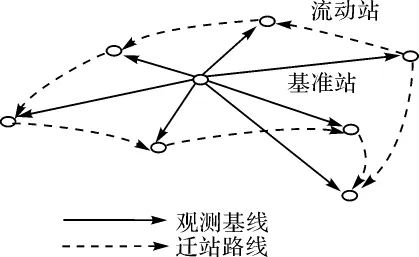
图2

四、转换模型的选择

常用的坐标转换方法为经典七参数法。用于基准转换的模型主要有布尔莎-沃尔夫(Bursa-Wolf)模型、维斯(Veis)模型和莫洛金斯基-巴代卡斯模型[3]。

该工程采用GPS做平面控制测量，高程控制采用常规水准来实现。因此，该模型只考虑二维平面的坐标转换，只需要四参数即可。基于转换高程异常的平面四参数法，相对于经典七参数法而言，所要求的条件较低，比较容易实现，同时避免了公共点高程精度不高引起的误差，更为可靠。

1．平面四参数法的数学含义

平面四参数坐标转换方法是一种降维的坐标转换方法，即由三维空间的坐标转换转为二维平面的坐标转换[3]，涉及两个平移分量、一个尺度因子和一个旋转参数。由于是平面二维的坐标转换，避免了高程系统不统一而引起的误差。

2．转换模型的基本思想

GPS测定的某点地心空间直角坐标系中的坐标为(Bi，Li，hi)，将其坐标转换为1980西安坐标系统下的一组近似平面坐标，如果假定四参数是精确已知的，利用四参数转换方法，则该点参心坐标系中的坐标(xi，yi)应为

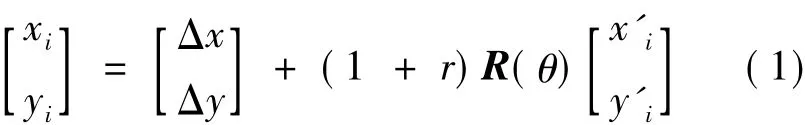
式中，Δx为坐标x的平移分量;Δy为坐标y的平移分量;r为尺度因子;

为求出4个参数，至少需要两个已知点，如多于两个点，则按最小二乘方法，求出转换参数，最终求出WGS-84平面坐标转换后精确的1980西安坐标系下的平面坐标。

3．转换模型的建立

如果认为1980西安坐标系所采用的椭球中心与WGS-84椭球中心重合，1980西安坐标系所采用的椭球短半轴方向与WGS-84椭球短半轴方向一致，则可以通过平面转换模型将GPS测定的大地坐标，转换成空间直角坐标。

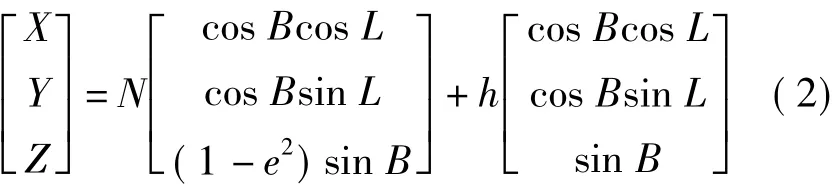
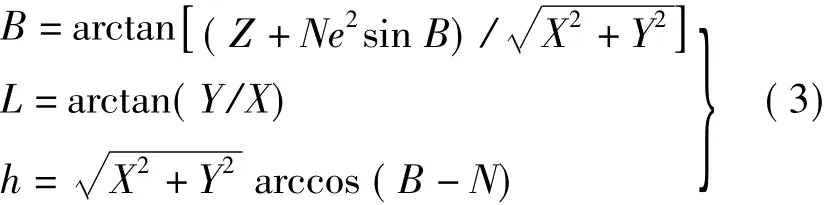
根据高斯投影正算公式，将1980西安大地坐标转换为高斯投影坐标(x'，y')

将式(1)代入式(4)，即可得到求得四参数的转换模型。

4．模型精度的验算及转换参数的求得

利用收集到的公共点，对模型精度进行精度验算和参数的计算。结果如表1和表2所示。

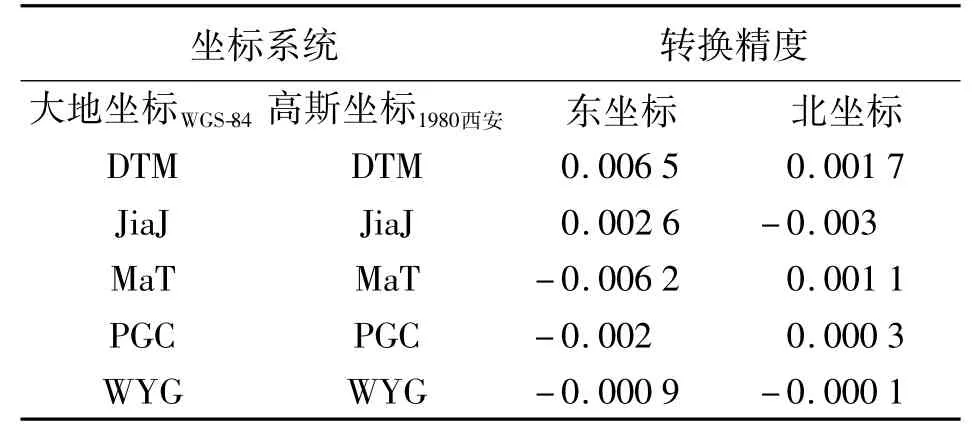
表1 转换精度验算

表2 转换参数成果表

五、方案的实施及精度分析

1．方案的实施

将基准站架设在基准点MaT上，另一流动站在场区各待定点上至少架设10min，得出相对于基准点MaT的WGS-84大地坐标，利用建立的转换模型将其坐标转换为工程需要的1980西安坐标下的格网坐标。

为了确定该方案的准确性，利用RTK放样测量方法，根据建立的转换模型，将已知点PGC实地放样，其精度达到厘米级，找到其实地位置。在有两个已知控制点的情况下，利用传统静态测量方法，得到场区各待定点的1980西安坐标下的格网坐标。通过上述方法相比较，该方案得出的结果稳定可靠。

2．坐标成果的精度

利用传统GPS静态控制测量方法和本文中使用的测量方案相比较，结果如表3所示。

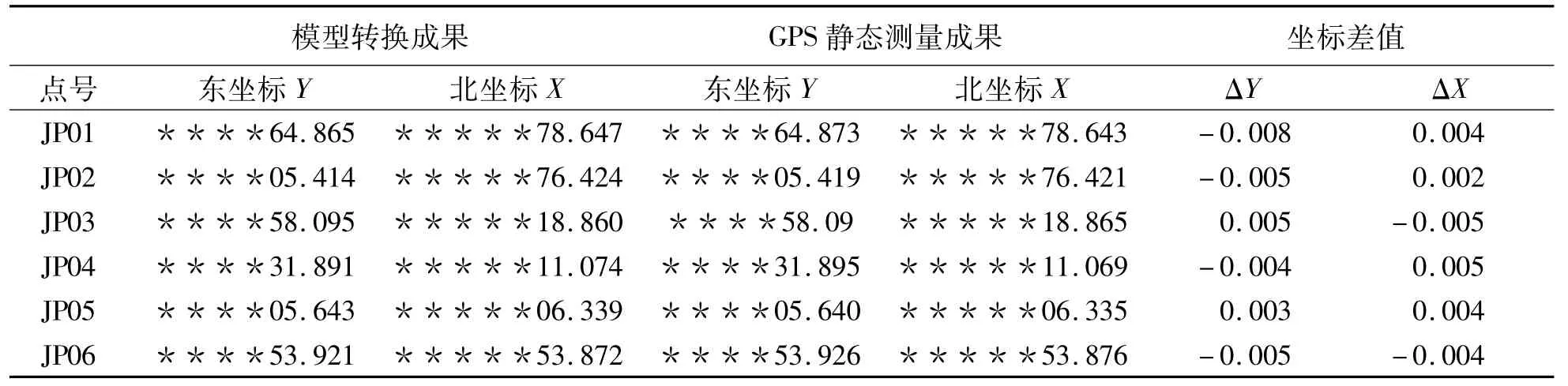
表3 成果对比m

3．外符合精度成果

利用该方法对收集到的已知点进行外符合检验，得到的结果如表4所示。

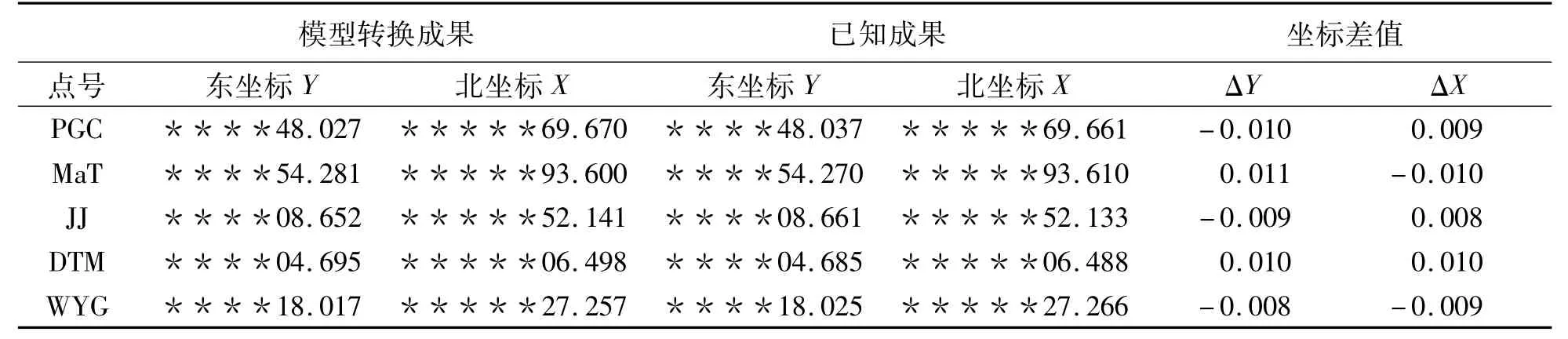
表4 外符合精度成果m

通过以上两个表格的数据，证明本文的方法在该工程条件下是准确的、可行的。

六、结 论

在收集到的控制点具有地心坐标和参心坐标的情况下，建立参心坐标系和地心坐标系的转换模型，将GPS观测得到的地心坐标成果，通过转换模型，转换成工程需要的参心坐标系成果，是可行的。通过本文所使用方法的尝试，可以得出如下结论：

1)在局域范围内进行工程测量(比如机场)，在收集的控制点均匀覆盖测区的情况下，利用本文中的方法，可以减少实地踏勘控制点的时间，大大提高工作效率。

2)本文方法要求收集到的控制点坐标既有准确的参心坐标，又有相对应的地心坐标，用以建立转换关系模型。

3)模型建立中，先利用一组精度不太高的转换参数，把地心坐标转换为近似的参心平面坐标，然后利用参心平面坐标的近似值与准确参心平面坐标值进行参与建模，可以简化建模过程。

[1]陈宇，白征东，罗腾．基于改进的布尔沙模型的坐标转换方法[J]．大地测量与地球动力学，2010，30(3)：71-73，78．

[2]中国有色金属工业协会．GB 50026—2007工程测量规范[S]．北京：中国计划出版社，2008．

[3]周忠谟．GPS卫星测量原理与应用[M]．北京：测绘出版社，1992．

[4]张勇．平面四参数法GPS坐标转换技术的应用分析[J]．城市勘测，2005(2)：28-30．