基于线路弧距的简支梁曲线桥墩台坐标计算

罗新宇

(兰州交通大学土木工程学院，甘肃兰州730070)

一、引 言

墩台定位测量是桥梁工程施工测量的重要内容，其关键是计算各个墩台中心的坐标。众所周知，曲线上的简支梁桥，桥上线路为曲线，而全桥的梁中线呈折线布置，线路中线与桥梁工作线不能吻合[1-4]，从而使得其墩台中心坐标计算成为墩台定位测量的一个难点。

简支梁曲线桥的墩台中心坐标计算最常用的方法是导线法[2-3]，即按照偏距→交点距→偏角→方位角→坐标的顺序依次计算，有些地方还要采用趋近法进行计算，其计算步骤繁琐，施工现场的技术人员难以掌握。本文提出一种基于墩台间线路弧距的墩台中心坐标计算方法，可以大大降低曲线桥墩台坐标计算的难度，便于施工现场的技术人员掌握，有利于利用全站仪或GPS进行墩台定位[4]。

二、计算原理

设Bi为第i号桥墩(台)中心，其坐标为，i为Bi在线路中线上的对应点，其坐标为为该对应点切线指向线路前进方向的坐标方位角，由于墩台中心与线路中心对应点的连线就是线路的法线，设Bi的偏距为Ei，则当线路左转时法线方位角等于切线方位角加90°;反之，当线路右转时法线方位角等于切线方位角减90°，所以有

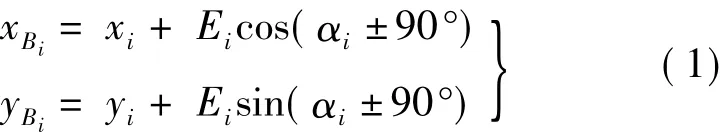
式中，当曲线右转时括号中的符号取减号。

可见，曲线桥墩台中心坐标计算的关键是确定该墩台中心Bi对应的线路中线点i的坐标、i点处线路切线的坐标方位角αi，以及墩台Bi的偏距。其中，与墩台对应中线点的里程有关，偏距Ei与梁的布置形式、墩台在曲线上的位置及曲线半径有关。

1．偏距计算公式

简支梁曲线桥主要有切线布置和平分中矢布置两种布置形式，计算偏距的公式也不相同。由于梁长远小于曲线半径，可以取E=f(切线布置)或E=f/2(平分中矢布置)，其中中矢f的计算公式如下[1]

圆曲线上

缓和曲线上

式中，L为相邻墩台的交点距，可用梁长加梁缝代替;R为圆曲线半径;t为计算点到缓和曲线起点或终点的距离;ls为缓和曲线的长度。

2．中线点里程计算公式

显然，曲线桥墩台中心坐标计算的关键是确定该墩台中心Bi对应的线路中线点i的坐标，以及i点处线路切线的坐标方位角，而确定坐标和方位角的关键是计算i点里程，这又可以根据前一点i-1的里程加上两点之间的弧距获得。

弧距计算可以按先直线再弧线的步骤计算[3]，本文给出直接计算弧距的方法。

图1中，1和2分别为两端墩台中心的线路对应点，由图1可见

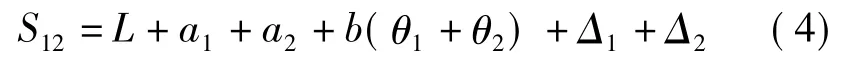
式中，L为梁长;b为梁的半宽;a1、a2为1点和2点处的最小梁缝之半;θ1、θ2分别为1、2点到梁中点M的弧长所对的夹角。设对应点处的半径为Ri，则有

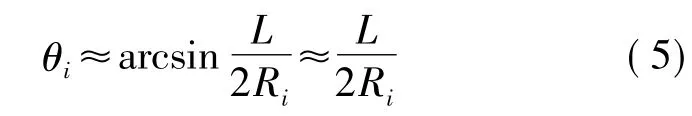
弧弦差Δi为

由此可得中线上对应点的里程计算公式为

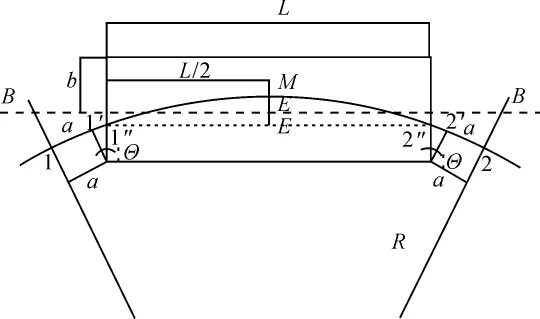
图1

3．中线点坐标计算

再以始端缓和曲线ZH为原点建立平面直角坐标系ZH—xy，x轴为ZH处切线，且指向交点方向为正向，自x轴顺时针90°为y轴，在此坐标系下ZH～Hy段任意曲线点A的坐标为[3]

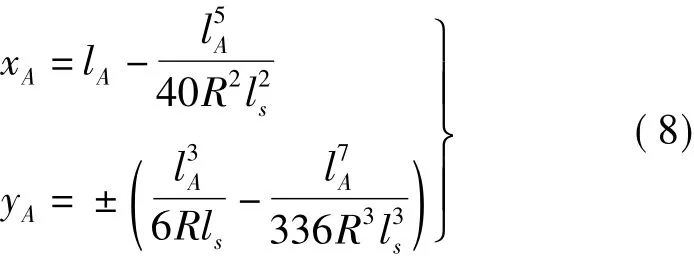
式中，lA为A点到缓和曲线起点的曲线长;ls为缓和曲线长;R为圆曲线半径。y坐标的取值规则是：按里程增加方向，当曲线右偏时y坐标为正，左偏时y坐标为负，下同。

Hy～yH段曲线点B的坐标为

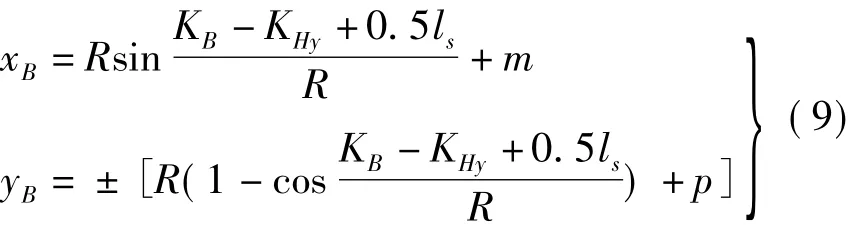
式中，KB、KHy分别为B点、Hy里程;m和p则分别是该曲线的切垂距和内移距。

yH～HZ段曲线点C的坐标按下式计算

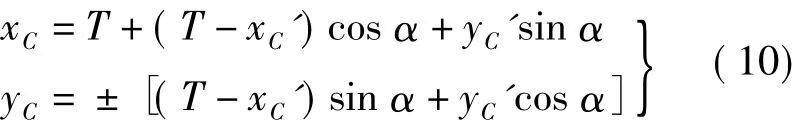
式中，T为曲线的切线长;α为线路转向角;(xC'、yC')为C点在末端缓和曲线坐标系中的坐标，设该点到HZ点弧长为lC，则根据缓和曲线方程式有

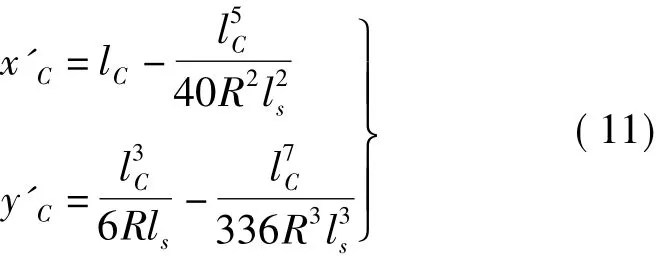
4．坐标方位角计算

仍以始端缓和曲线的起点ZH为原点，以ZH切线为x轴，且指向交点方向为正向，建立右旋平面直角坐标系ZH—xy，则ZH～Hy段的曲线点A在此坐标系下的坐标方位角为

式中，lA为A点到缓和曲线起点的曲线长;l0为缓和曲线长;R为圆曲线半径;曲线右转时取正号。

Hy～yH段曲线点B的坐标方位角为

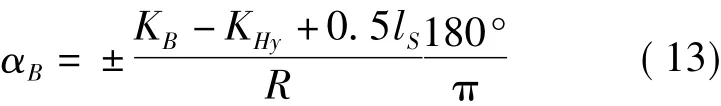
yH～HZ段曲线点的坐标方位角为

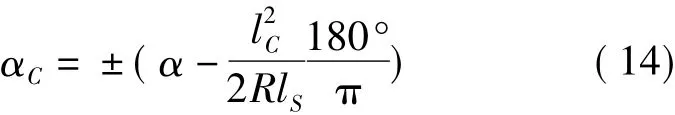
式中各符号含义以及公式中的符号取值同前。

三、计算步骤

1)计算曲线要素和主要点里程;

2)确定梁长L、梁半宽b，和梁两端的最小梁缝之半 a1、a2;

3)按式(4)～式(7)计算弧距和里程;

4)按式(8)～式(11)计算中线上的桥墩对应点坐标;

5)按式(12)～式(14)计算对应点处的法线方位角;

6)按式(2)或式(3)计算矢距f，并根据桥梁的布置形式计算外移距E;

7)按式(1)计算墩台中心坐标。

四、结束语

根据曲线简支梁桥上相邻两墩台之间的线路中线几何关系，直接计算中线弧距，进而通过计算中线点坐标和坐标方位角，进一步计算出桥梁墩台中心的坐标，这种基于中线弧距计算的方法，几何关系清楚，计算公式简单，可以大大降低曲线桥墩台坐标计算的难度，便于施工现场的技术人员掌握。

[1]胡鹏，丁克伟，夏顶．弯桥上简支梁板布设法的探讨[J]．安徽建筑工业学院学报：自然科学版，2011，19(2)：11-14．

[2]王承礼，徐名枢．铁路桥梁[M]．北京：中国铁道出版社，1990：372-377．

[3]姚德新．土木工程测量学教程[M]．北京：中国铁道出版社，2009：169-179．

[4]孙亦环．铁路桥涵[M]．2版．北京：中国铁道出版社，2006：61-66．

[5]吕建明．公路铁路曲线桥梁坐标定位法及其通用程序[J]．科技开发与经济，2000，10(3)：58-59．