回归分析法在GPS测量坐标变换的应用

钟连琨

(广西国土测绘院，广西南宁530023)

一、引 言

全球定位系统(GPS)自20世纪70年代产生，由于GPS具有全天候、高精度、自动化、高效益等显著优点，已经广泛应用于大地测量、工程测量、车辆导航、航海导航等领域。GPS采用1984年世界大地坐标系(world geodetic system 1984，WGS-84)是一个协议地球坐标系，坐标系的坐标原点位于地球的质心，其空间直角坐标系的Z轴指向AIH1984定义的地极方向，X轴指向AIH1984的起始子午面和赤道的交点，采用椭球参数为：a=6378137m，f=1/298．257223563。而我国测绘系统广泛采用的是北京54坐标系和西安80坐标系。北京54坐标系源自于原苏联采用的1942年普尔科夫坐标系，参考椭球是克拉索夫斯基椭球，椭球的参数为：a=6 378 245 m，f=1/298．3。西安80坐标系采用IAG1975椭球，椭球的参数为：a=6 378 140m，f=1/298．257，地球椭球的短轴平行于地球质心，指向JYD1968的方向，起始子午面平行于我国起始天文子午面。从上可见，上述这些坐标系之间不但坐标原点不一致，而且各坐标轴之间相互不平行。所以，在实际应用中，必须进行坐标转换。目前，不同坐标系间坐标变换的通常方法有相似变换法、三参数法、七参数法等。这些方法都是对空间中的图形进行平移、旋转以及缩放等的变换，它们都具有几何关系明确、解答参数方便、变换公式规则、可以适当外推的优点，但对坐标系的局部变形顾及较差。由于测量不可避免误差，如折光误差、尺长误差、信号传播误差等，使得系统中各点的坐标值并不严格处于确定的数学模型下，从而使得各坐标系统中产生局部性或整体性偏差，于是就存在变换模型的适度问题。1954年北京坐标系是由原苏联大地网延伸过来的经，所提供的点的坐标是局部平差的成果。为了建立我国独立的大地坐标系，从1972年开始，历时10年完成了全国天文大地网建设工作，并对全国一、二等三角锁网、部分三等三角锁网和导线共48 433点进行整体平差，建立了“1980年国家大地坐标系”。由于布设时代不一，时间久远，参与整体平差和不参与整体平差的点精度不一，再加上地壳运动，它们之间的局部性误差和形变是不可避免的。此时坐标系之间的真实变换关系是非常复杂的，并不是确定的几何关系。如采用相似变换法、三参数法、七参数法不可避免带有模型误差。而采用回归分析法可将系统的偏差拟合到回归参数中，更加完善地进行不同坐标系间的转换，获得较高的坐标变换精度。

二、回归分析法的原理

回归分析是统计学中的一个重要分支，在自然科学领域和社会科学领域有着十分广泛的应用，是处理多个变量之间相关关系的一种数学方法。它是建立在对客观事物进行大量试验和观测的基础上，用于寻找隐藏在那些看上去是不确定的现象中的统计规律的数理统计方法。按照控制论的观点，一个系统的内部结构并不清楚，但是只要掌握了它外部联系的状态方式，阐明它输入和输出的因果关系，就可以认为充分掌握这个系统。在坐标转换中，将不同坐标系之间的变换过程视为黑箱，输入的是变换前坐标系的旧坐标，输出的是新坐标系的新坐标。应用回归分析方法建立输入和输出之间的数学关系，从而确定它们之间的变换关系。坐标变换回归分析主要有下列几方面的内容：

1)从一组数据出发，分析变量间存在什么样的关系，建立这些变量之间的回归模型;

2)对回归模型的可信度进行统计检验;

3)从影响某一个变量的许多变量中，判断哪些变量的影响是显著的，哪些是不显著的，从而建立更实用的回归模型。

三、回归分析坐标变换的模型

多元线性回归的模型如下。

设因变量为Y(预测对象);自变量为X;(xi，yi)是 X、Y 的观测值，其中 i=1，2，…，n。

则可以建立多元线性回归方程

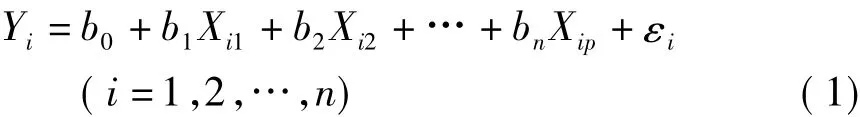
式中，b0、b1、b2、…、bp是未知参数的回归系数;εi是随机误差，其方差为σ2其矩阵形式为

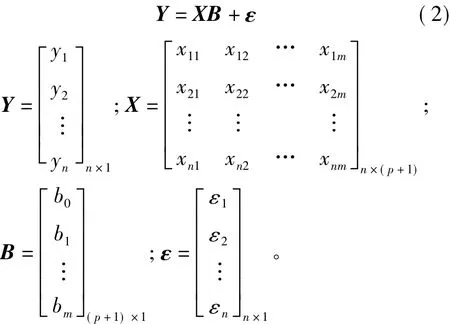
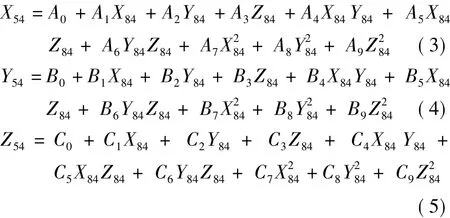
每个空间分量的矩阵形式为

根据最小二乘法原理有

回归模型的系数为

四、算 例

现有下列一组北京54和WGS-84两坐标系统公共点的观测数据表1，由于空间坐标(X，Y，Z)3个分量都是独立的，现以X分量为例来讲述坐标变换回归模型的建立过程。

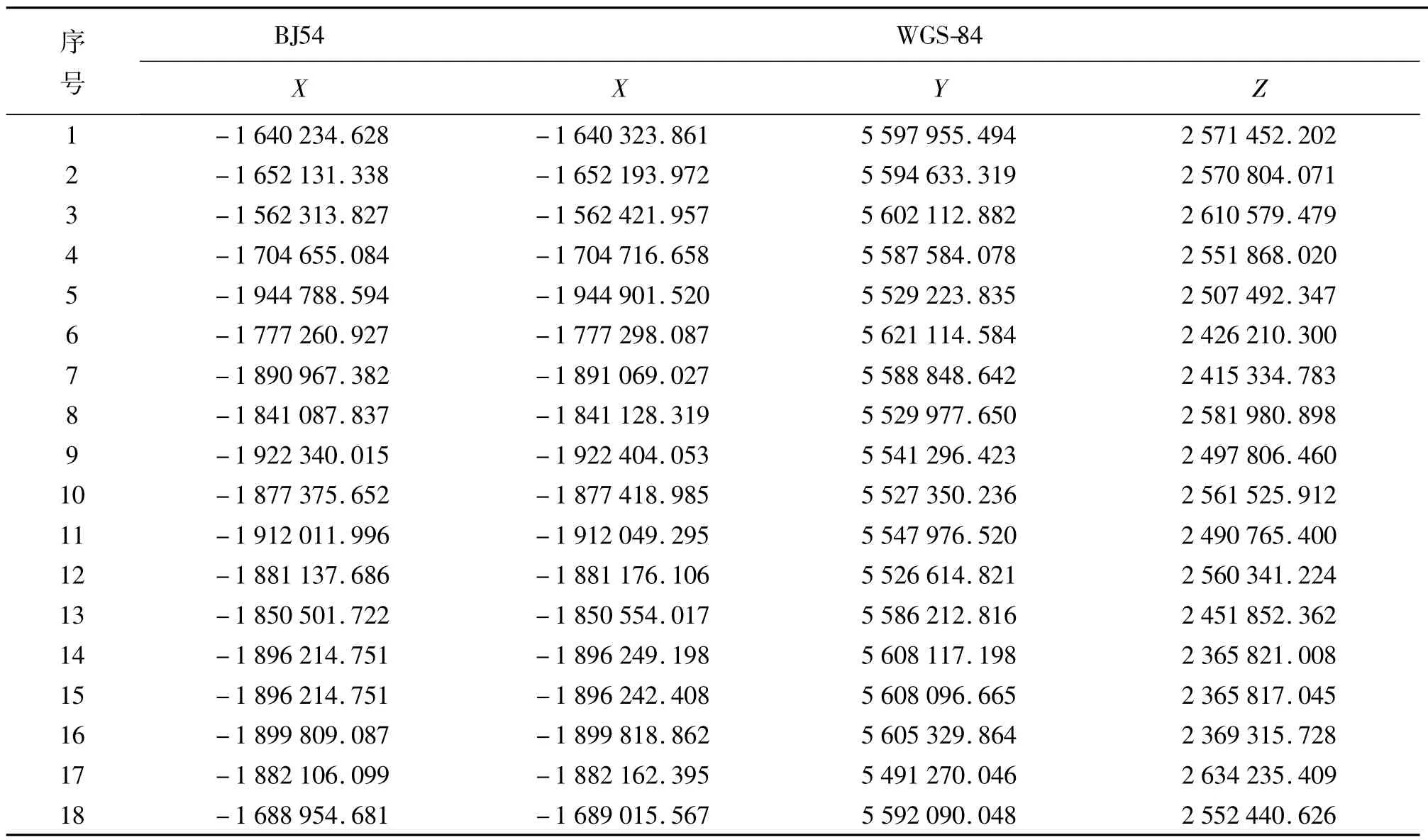
表1 m

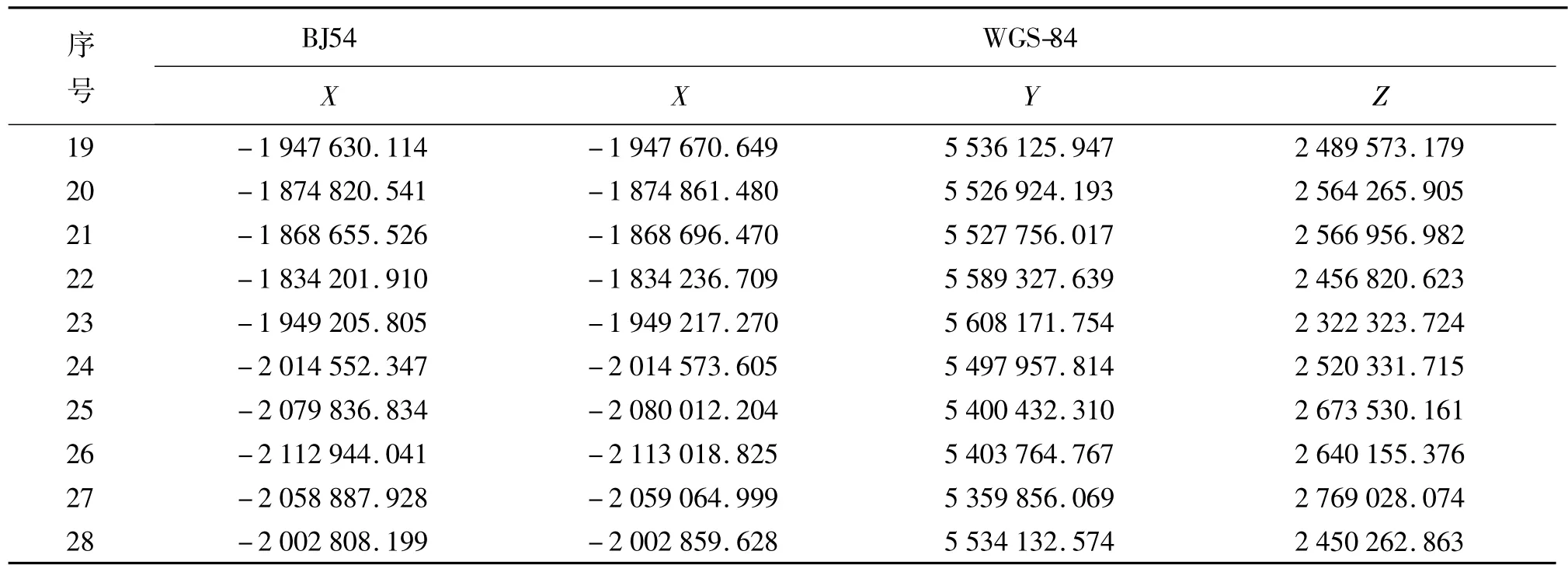
续表1

1．回归模型的构造

为了计算上的方便，可以用先求出坐标增量方式来求出转换坐标。另外，由于本例的公共点不是佷多，为了等价于7参的转形式，选择6个参数来构造回归模型。具体构造方程如下

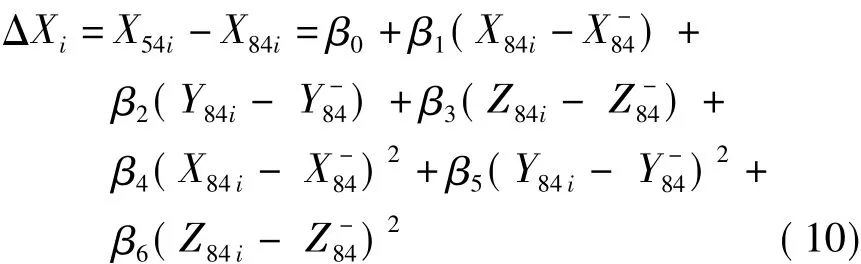
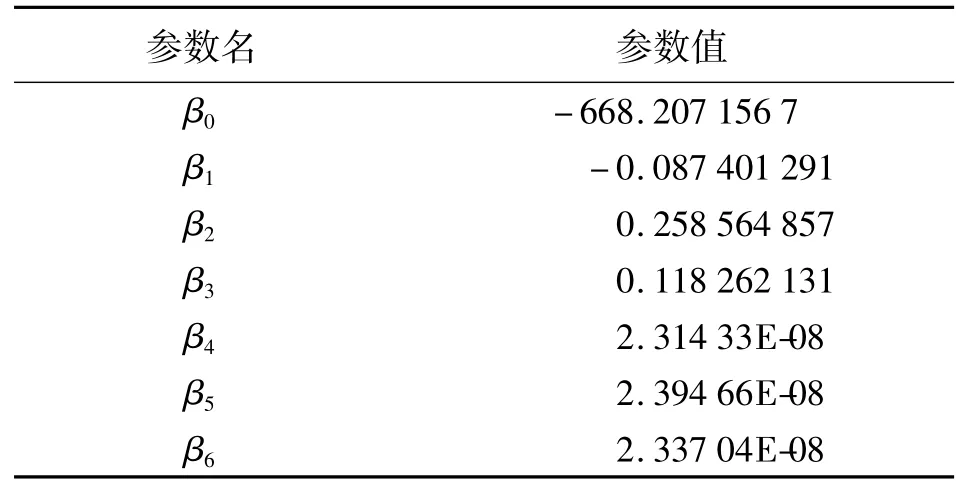
表2

2．回归模型的检验

(1)模型拟合优度检验

根据赤池信息准则(akaike information criterion)有

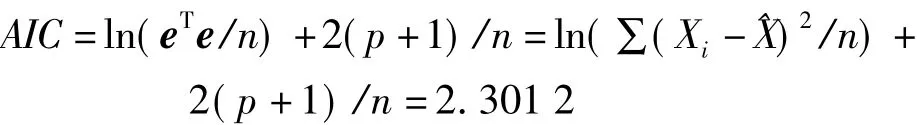
由于AIC=2．301 2，其数值较小，故模型拟合程度较高。

(2)模型显著性的检验

根据回归分析的方法，对其检验的过程归纳为表3。

在给定的显著水平 α =0．05，F(6，21)=2．57 ＜F=(SSR/p)/(SSE/(n-p-1))=23 044 963 066．74，故回归模型是显著的。

(3)模型系数显著性的检验

对于回归模型，回归模型是显著的，并不能说明每个参数对坐标变换的影响是显著的。要检验某个参数对坐标变换的影响是否显著，等价于检验相应的回归模型的系数是否显著的不为0，这就是回归模型系数显著性检验，通过t检验来完成，有

对回归模型系数βj(j=1，2，…，p)的检验。本例的计算结果如表4所示。

表3 回归模型显著性检验的方差分析

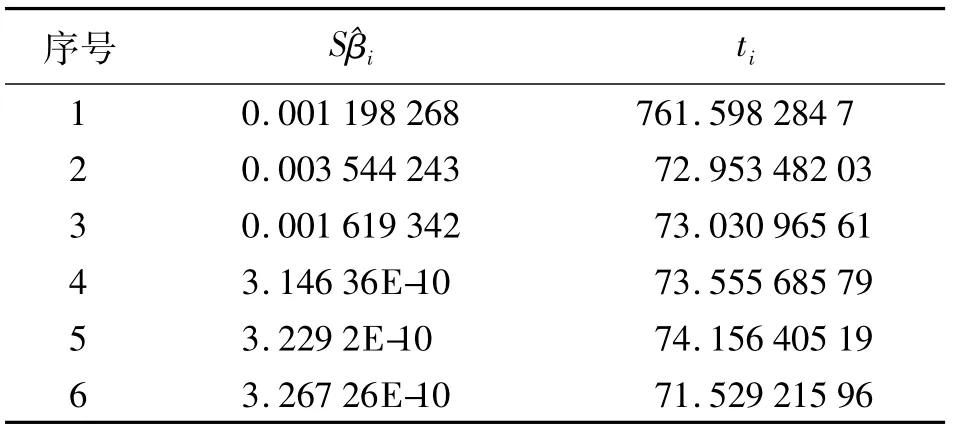
表4 回归系数显著检验

t0．025(21)=2．080 ＜ ti，故在显著水平 α =0．05条件下，该回归模型系数是显著有效的。

五、结束语

1)当变换的区域较小且公共点数量有限时，回归的模型实质就是相似变换。

2)在模型的选择上，高阶项目具有极其不稳定性的特点，使用时要特别小心。

3)选择的参数个数的多少，受公共点的数量限制，选择的方案应确保有足够的多余观测量。由于过多的回归参数表面上会使R2增大变换精度提高，但实际上可能是虚假的，因此选择参数在不影响变换精度的前提下，应选择比较简单的模型。

[1]王福保．概率论及数理统计[M]．上海：同济大学出版社，1998．

[2]周富臣，王生辉，易英，等．常用数理统计方法及应用实例[M]．北京：中国计量出版社，2006．

[3]刘大杰，施一民，过静珺．全球定位系统(GPS)的原理与数据处理[M]．上海：同济大学出版社，1997．

[4]朱华统．大地坐标系统的建立[M]．北京：测绘出版社，1986．

[5]钟连琨．平面相似变换在地面网与GPS网平差连接中的应用[J]．测绘工程，1999(2)：58-62．

[6]钟连琨，黄发秀．GPS水准拟合方式的统计分析及拟合方式的选择[J]．工程勘察，2000(5)：15-18．