航测单模型(m+1)(2n+1)个标准点的相对定向
牛卓立
(中国有色金属工业西安勘察设计研究院,陕西西安710054)
一、引 言
在文献[1]中推导了航测单模型采用6个标准定向点,单个测点和一个双片像对全部测点的平均中误差计算公式。本文将模型在航向方向m等分,在垂直航向方向2n等分,以(m+1)线和(2n+1)线的交点共(m+1)(2n+1)个标准点为定向点,推导了任意测点和全模型的平均中误差计算公式。
二、(m+1)(2n+1)个标准点的相对定向元素的权倒数矩阵
误差方程式
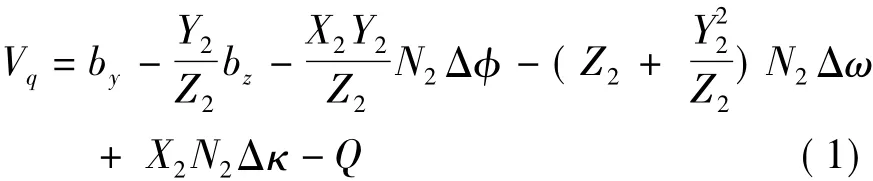
式(1)引自文献[2],与文献[3]公式符号有差异。(m+1)(2n+1)个标准点为定向点时,误差方程式系数如表1。类似表1还有m个表,此处省略。
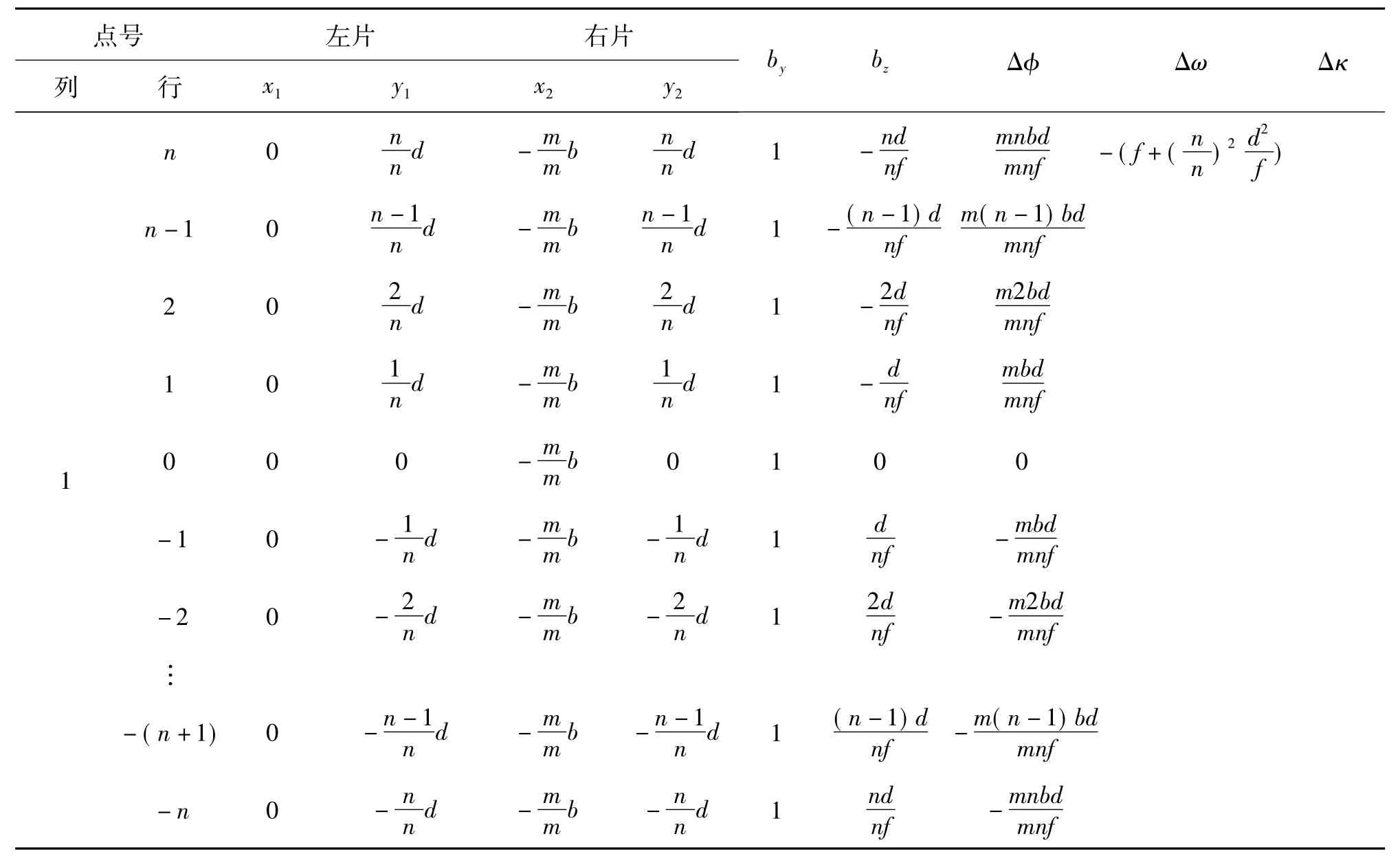
表1 (m+1)(2n+1)个标准点定向时误差方程式系数表
按表1组成法方程式,见表2。

表2 相对定向法方程式系数表
表2中代号的计算公式如下
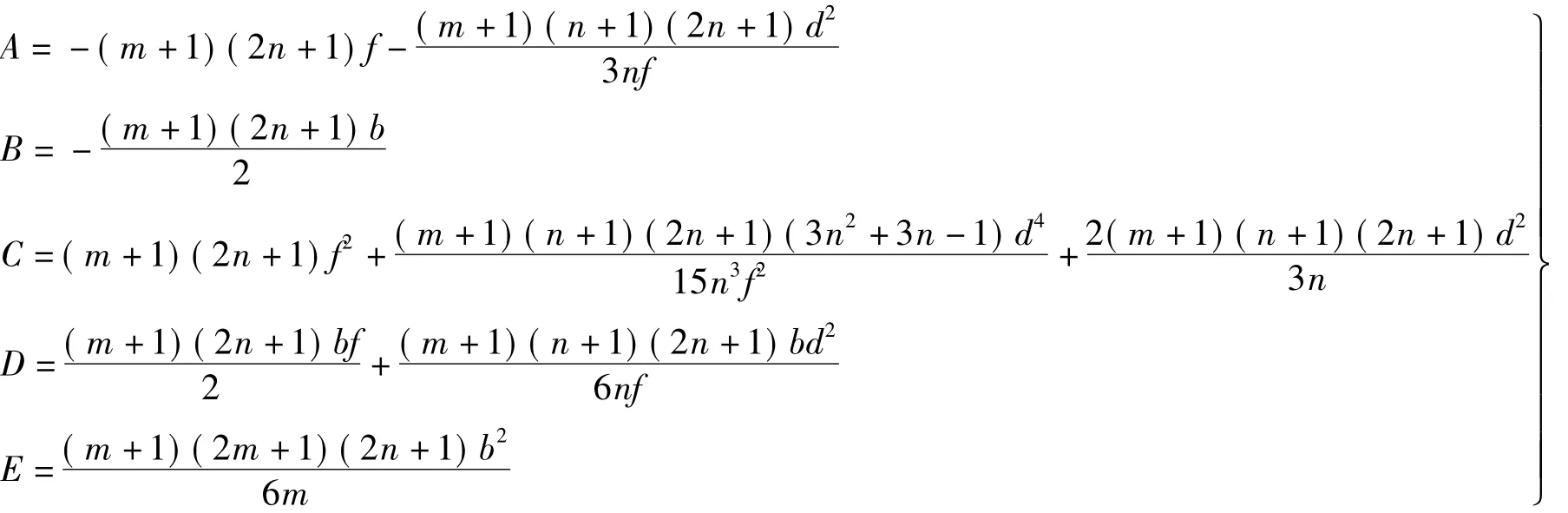
解表2法方程式,得其逆矩阵如表3。
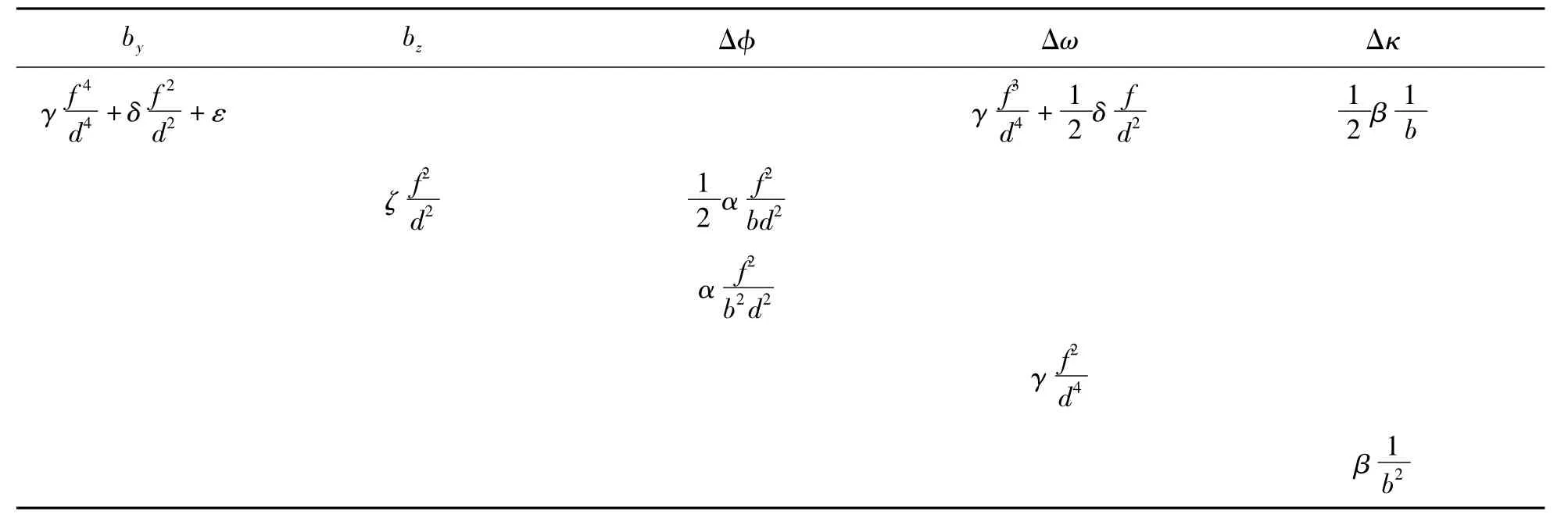
表3 相对定向元素的权倒数矩阵
表3中一些代号的计算式如下:

三、模型内任意量测点权倒数计算公式
模型内任意测点权倒数计算公式可按熟知的误差传播公式进行。可参照文献[1]进行,不再赘述。Q的计算见表3。
四、模型平均权倒数
任意模型点的权倒数与其位置有关,为总体考察全模型的精度,以利于工程的技术设计应用,为此,在 b×d范围内,取 ΔX2、ΔY2、ΔZ2各自积分的均值得一个模型的权倒数的平均值如下
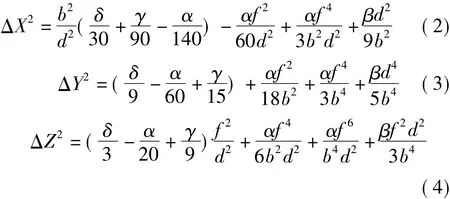
因当前的航测数码摄影机焦距一般都大于成图范围(b×2d),为简化计算,将式(2)、(3)、(4)展开为幂级数并取各式的主项对技术设计已足够应用,得
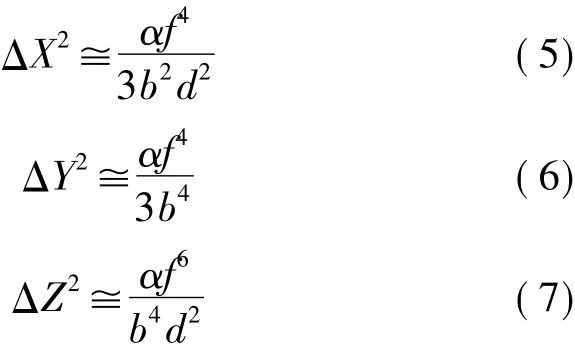
平面位置权倒数(赫尔默特)
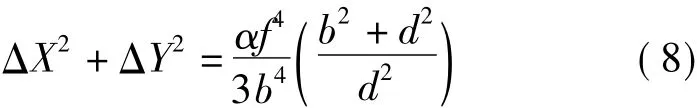
高程权倒数

五、基线分量的权倒数
基线分量的权倒数bx由ΔX=x1-x2算出,by和bz由表3直接给出
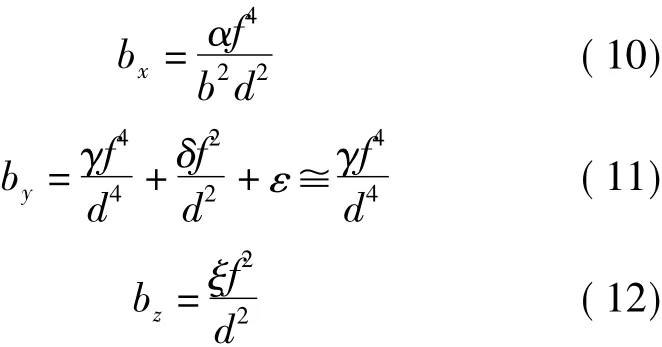
六、模型误差计算
平均平面位置中误差(赫尔默特)按下式计算
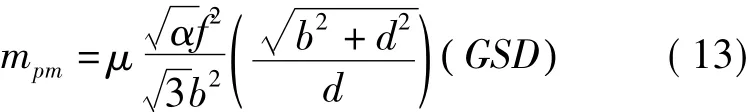
高程中误差按下式计算
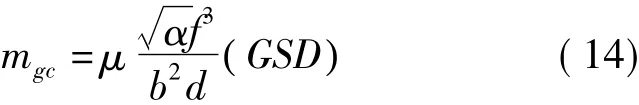
式(13)、(14)中,μ为观测单位权中误差,单位为像素;GSD为地面分辨率,单位为长度单位/像素。
七、结束语
标准点个数不同对平面或高程误差(式(13)、式(14))主要表现在α的减小上,见表4。
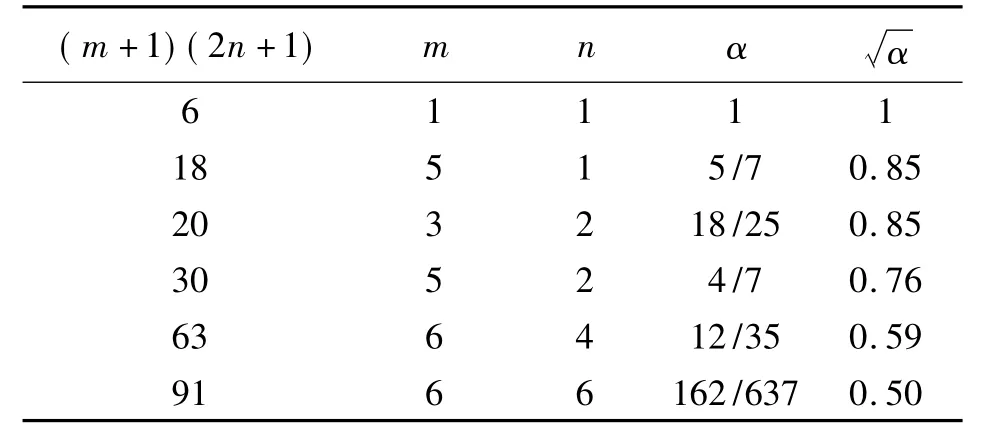
表4 标准点个数与系数α
[1]牛卓立.航测单模型误差分析[J].工程勘察,2012,40(7):66-67.
[2]李德仁,王树根,周月琴.摄影测量与遥感概论[M].北京:测绘出版社,2001:57.
[3]王之卓.摄影测量原理[M].北京:测绘出版社,1970:30.

