方格网法土方量计算及误差影响

王铁生，程鹏里，赵东保，缑慧娟

(华北水利水电学院土木与交通学院，河南郑州450011)

一、引 言

土方量测量是在土方施工中经常要进行的工作，它关系到施工进度的掌握、工程量的计算和资金的结算。在整个工程中，土方工程往往也是很多大型工程中重要的环节，但是土方量的计算是个复杂的问题，一般是不准确的，存在误差。在计算土方量时一般允许误差为10% ～20%，主要因为土方量计算受到场地整平时的坡度、计算方法、施工验收方法、土的松散系数以及等高线的高程误差等因素的影响。一般认为等高线的高程误差对于土方量的影响应小于5%。但是对一些大型土方工程，即使是5%土方误差，工程费用偏差也是相当大的。所以大土方工程中，减少方量计算的误差，提高其精度，颇具现实意义[1]。在计算土方量时，一般要求土方量最小，且填挖量平衡。高程的精度作为影响土方量结果的一个重要影响因素之一，是在计算土方量时必须考虑的一个内容。

二、施工高度中误差的计算

土方量计算方法很多，包含断面法、方格网法、等高线法、DTM法等。由于正方形方格法是常采用的土方量计算方法之一，以下主要针对方格网法进行土方量施工高度精度分析。

在进行土方量计算时，必须先计算内插点的高程，影响施工高度中误差的因素为等高线的高程误差和图上量测误差。量测误差随着比例尺、等高距和地形坡度不同而不同。设施工高度中误差为mh。设场地的设计高程为h设，方格网顶点的高程即自然地面高程为h实，根据设计高程和方格网顶点的高程可以计算出每个方格网顶点的挖填高度[2]，即高程之差hi为

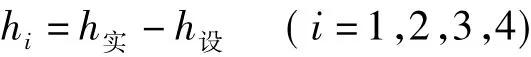
而

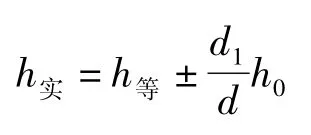
式中，d为内插点的高程时，过内插点与相邻两条等高线正交时图上的线段长度;d1为内插方格网顶点时，内插点到相邻两条等高线的垂直距离中较短的一条;h0为地形图等高距;h等为位于等高线上的点的高程

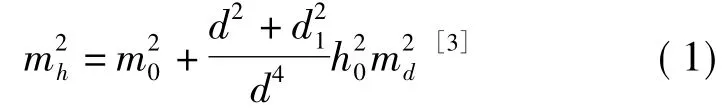
式中，m0为等高线高程的中误差，约等于1/3等高距;md为内插等高线高程时图上长度量测的中误差。在式子中，考虑到最大影响d=0．5d，则1

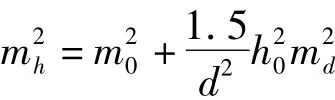
即

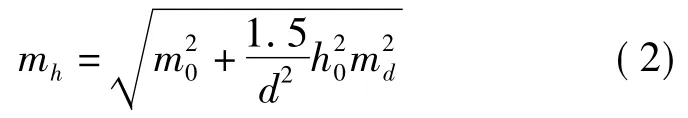
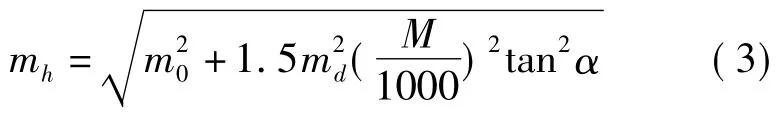
在实际计算中你会发现公式(3)中后面一项(即直线在不同比例尺和坡度条件下丈量的长度误差)

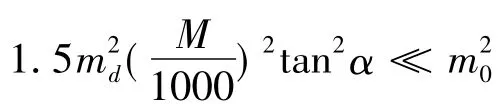
对公式的结果影响很小，而且在目前数字测图的情况下[4]，不存在图上量距误差的影响，总而言之，公式(3)中的后面一项完全可忽略不计。即公式可简写为：mh=m0。在平坦地区等高距一般为0．5m，则

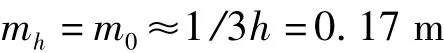
通过以上公式对施工高度中误差的估算，可以得到一般情况下进行土方量计算时，施工高度可以达到的精度。根据这个条件可以对不同面积的条件下进行方格网边长的约束分析。

三、方格网法计算土方量时施工高度中误差的计算

方格网法计算土方量时，通常将地面分成规则的矩形地块，原则是细分到是每一网格的地块高程相等[5]。但在实际操作中不可能相等，必然存在误差，高程误差是影响土方量精度的一个重要因素，是计算土方量相对中误差的一个重要因子。现根据方格网计算土方量的公式，利用误差传播定理来推求施工高度中误差。

1．施工高度中误差的估算

测绘出版社出版的“工程测量学”教材中，对施工高度的中误差的计算，是在计算土方量的相对中误差的基础上来推导的。

设场地面积为正方形，用方格网法计算土方量时，由计算的每个小方格网的体积求得总体积。现在设小方格网的边长为s，所以每个小方格为一个棱柱体，则其体积为

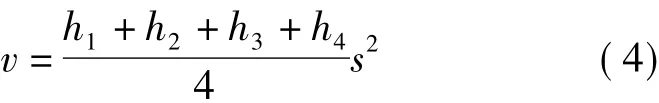
式中，hi(i=1，2，3，4)认为其中误差相等，设其值为mh，则棱柱体的中误差为

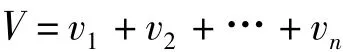
故

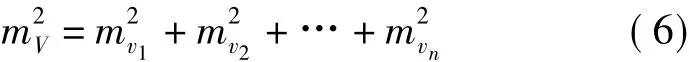
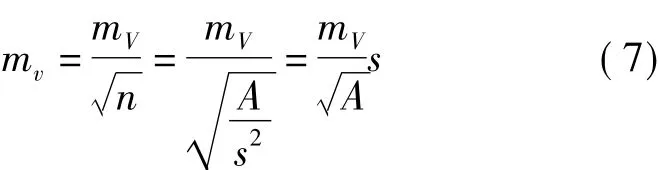
如果场地所填(或挖)的平均高度为h均，则V=Ah均，再有式(5)和式(7)即可的得

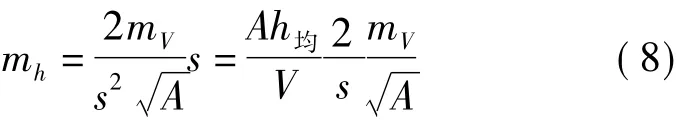
即

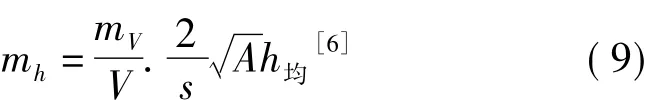
在这个公式推求中，根据误差的传播定理[7]可以发现公式(6)是不严密的。因为在计算土方量时，各个小方格网上点的高程不是使用一次，所以各个小方格网计算的土方量体积不是相互独立的，具有一定程度的相关性，不能把各个小方格网计算的土方量的中误差简单相加。在这个基础上推求了一个更加严密的计算施工高度中误差的计算公式。

2．改进的施工高度中误差的计算

为了推求一个更加严密的施工高度中误差的计算公式，设与一个方格相关的方格点(角点)，其高程的权为1;与两个方格相关的方格点(边点)，设其高程的权为2，与4个方格相关的方格点(中点)，设其高程的权为4[8]。则h均的一般式为

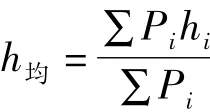
设整个方格网边长为L，测量时产生的中误差为mL，A=L2=ns2，根据误差传播定律，可以得到mA=2LmL。场地为正方形，整个方格网中无拐点，L=■ns，所以

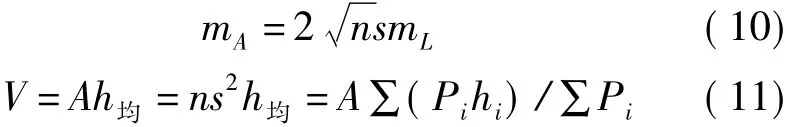
根据误差传播定理可得

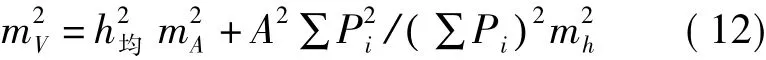
把式(10)代入式(12)中可得

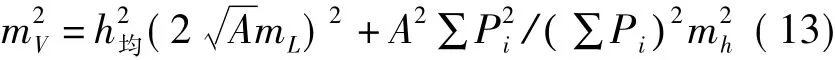
则土方量的相对中误差由式(11)和式(13)可得

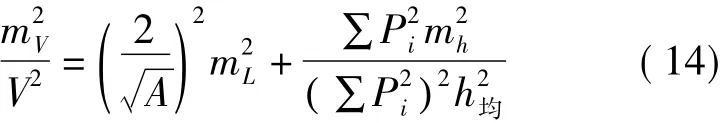
由于整个方格网无拐点，所以

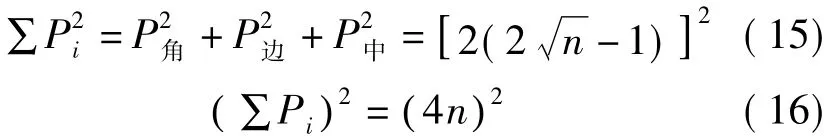
把式(15)、式(16)带到式(14)可得

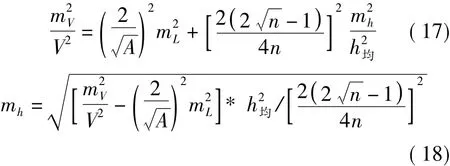
由于面积A一般是个比较大的数值，而mL远远小于A，所以式(18)可以简化写为

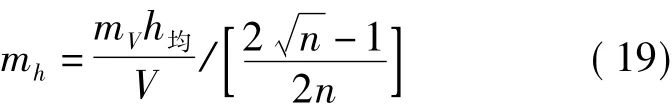
因为A=ns2，所以，结果代入式(19)中即可得

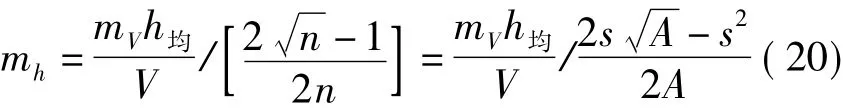
四、实例分析

根据上面推导出的公式(9)和公式(20)，现计算不同边长和面积条件下对应的施工高度中误差的值。计算结果见下表1。

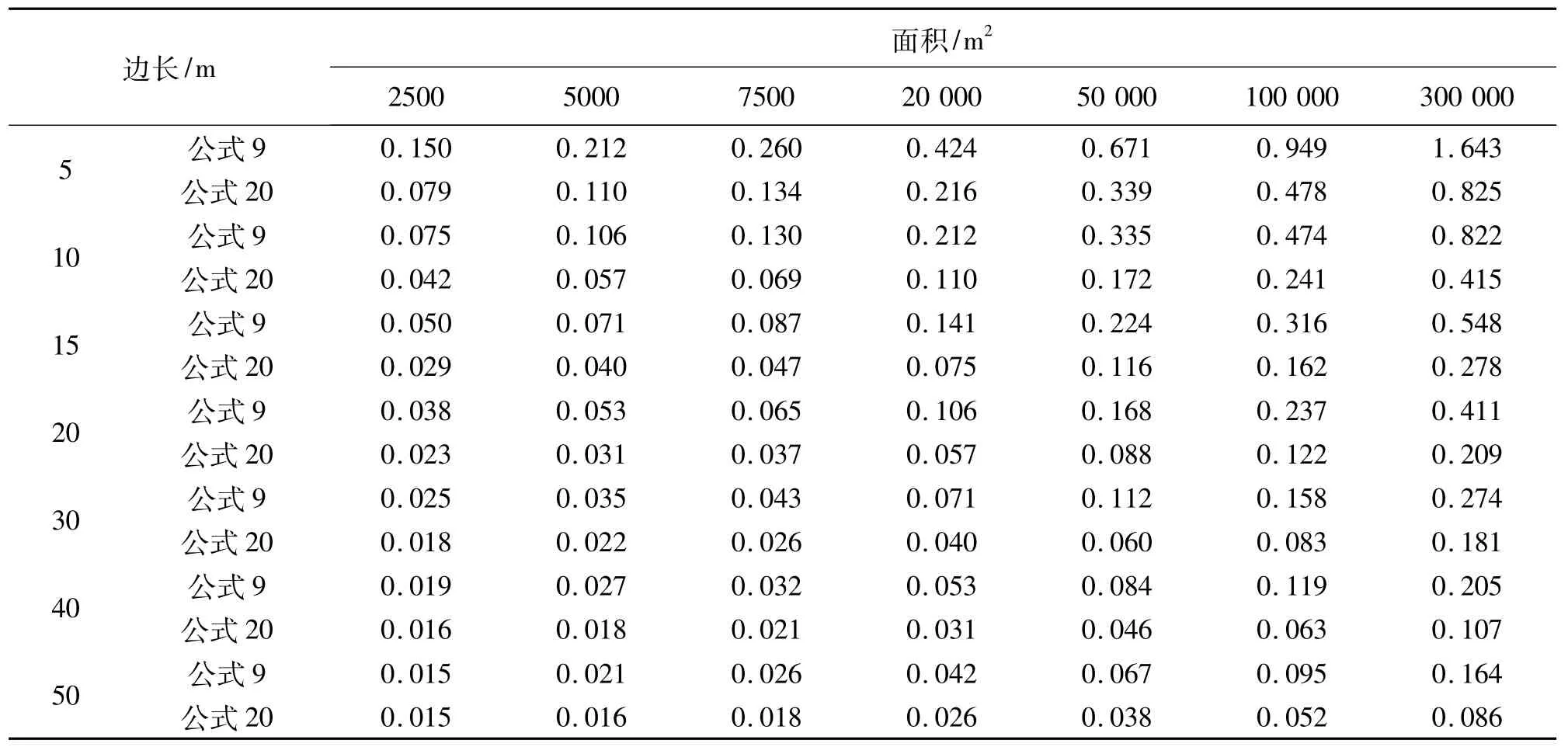
表1 施工高度中误差

在从表中可以看出：

1)在不同的面积和边长条件下计算出来的施工高度，公式(20)比公式(9)都更加精确，但要求的条件更严格。例如在面积为50 000m2时，要达到高程误差对土方量的影响限值的5%的一半，按照公式(9)，方格网边长为20 m时，对施工高度中误差的精度要求为0．168 m。但在公式20中对施工高度中误差的精度要求为0．088 m。而在实际工程中，地形图的等高线高程误差一般不易达到这个精度，所以，如果按照公式(9)的结果，在边长为20m的条件下计算土方量一定达不到高程误差对土方量影响限值5%的一半。只有在边长为10～15m或更小的条件下才能到达要求。

2)在计算土方量时，当施工面积为5000 m2或者更小时，方格网边长不能超过5m，在边长为40m时，施工面积只有在300 000 m2以上时施工高度才能在误差的要求范围之内，即方格网边长一般不要超过40m。

3)当方格网小，而面积较大时，求得的施工高度中误差很大，所以在实际工程中，此要求很容易满足，但施测密度变大，工作量会明显增加;而当面积较小，方格网边长较大时，求得的施工高度中误差较小，在实际工程中，一般很难达到这个要求。从计算的数据中可以简单得到：面积50 000 m2时，方格网边长不要超过15m;面积为100 000m2时，方格网边长不要超过20m。

五、结束语

为了满足土石方工程量计算的精度要求，对不同的施工场地面积应选用合适的方格网边长。当方格网小，面积较大时，要求的施工高度精度可以较低;而当选取的方格网边长较大时，为了保证土方量精度，就会对施工高度的精度要求较高;从前面的施工条件和计算数据分析结果不难分析得出，为了保证土方量计算精度，通常情况下方格网边长应在10～40m范围之内，最大不应超过50 m;改进后的公式更加严密精确，但要求的条件更加严格，按现在的数字测图方法和技术，亦能实现;如果整平的总面积和施工高度增加，要求的施工高度精度还可降低。

[1]何晗芝．工程土方量计算方法优化分析及其程序实现的研究[D]．长沙：湖南大学，2009．

[2]王铁生，袁大奇．测绘学基础[M]．郑州：黄河水利出版社，2009：218-222．

[3]张海印．土方精度与方格网边长之关系的研究[J]．华东地质学院学报，2000(3)：69-73．

[4]潘正风．数字测图原理与方法[M]．第二版．武汉：武汉大学出版社，2009：23-27．

[5]王先鹏．土方量计算的原理与方法及ArcGIS的应用前景[J]．地理空间信息，2009(8)：139-141．

[6]李青越．工程测量学[M]．第三版．北京：测绘出版社，2008：14-17．

[7]武汉大学测绘学院测量平差学科组编．误差理论与测量平差基础[M]．第二版：武汉：武汉大学出版社，2009：41-47．

[8]张正禄．工程测量学[M]．武汉：武汉大学出版社2011：117-119．