七参数坐标转换及C++程序实现

何群森，王婷婷，陈绍杰

(龙岩学院资源工程学院，福建龙岩364012)

在城市工程建设布置测量控制网的时候，测绘成果不仅要满足测图比例尺的需要，而且还要满足工程施工放样的需要。在工程施工放样时，常常要求两控制点间的距离与坐标转换的距离尽可能一致，但由于中央子午线都是按照一定的投影带分隔的，测区可能会偏离中央子午线比较远或者测区海拔相对较高，就会造成测量结果长度发生了变形，不能满足工程测量的精度要求[1]。当遇到一些相对较大的工程时候，在做控制测量时，精度可能达不到工程的需要，不能满足工程放样需要。在做边桩放样时，常常需要实际测量的长度与所测的长度尽可能要保持一致，尽可能的减小长度变形所带来的影响，这个时候就急需建立工程独立坐标系[2]。另外，在我国一些高程相对较高的地方，由于测量精度的需要，采用国家坐标系不仅不能满足实际工作的需要，反而会产生一些不必要的问题，所以就要建立一个适合工程测量的独立坐标系[3]。因此，为了解决这个问题，需要建立一个独立坐标系。

当一个工程有国家坐标系和独立坐标系时，为了工程使用的方便，根据不同坐标系间的转换关系，以独立坐标系为基础将国家坐标系向独立坐标系转换，以形成一个整体的统一独立坐标系[4]。本文则在探讨了坐标系转换方法的基础上，以七参数坐标转换原理编写三维坐标转换软件，并以实例验证。

一、直接参数法坐标转换原理

CASS软件中坐标转换即根据直接参数法转换原理，利用两套坐标系两个已知公共点的坐标(X1，Y1)、(X2，Y2)、(x1，y1)、(x2，y2) 求出坐标转换平移参数、尺度因子、旋转参数。其坐标转换的数学模型如下[5]。

(1)分别计算两个公共的坐标增量

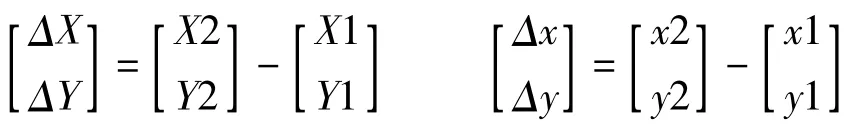
(2)分别计算两个公共点的距离

(3)计算方位角

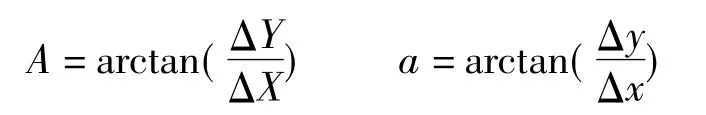
旋转参数θ=A-a。

(4)计算其他点(Xi，Yi)转换后的坐标

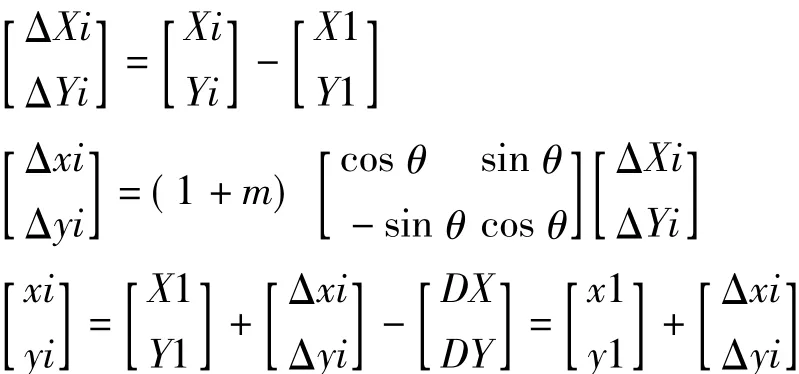
直接参数法虽然方法简单且技术上比较容易实现，只要待转换点附近有两个已知公共点的两套坐标，就可实现转换，但是该方法只能对平面坐标转换不能对高程转换。

二、七参数法坐标转换原理

七参数法，是本次试验所采用的坐标转换原理，该方法需要3个或3个以上的已知公共点才能转换，其优势在于不仅能转换高程，而且转换结果相对比较高。利用两套坐标系中3个或3个以上已知公共点的坐标，求出3个平移参数，1个尺度因子，3个旋转参数[6]，其坐标转换模型如下

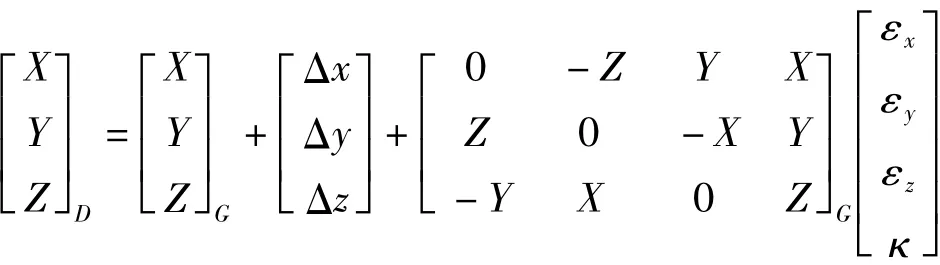
上式是七参数法模型的简化形式。其中包含7个转换参数，即3 个平移参数：Δx、Δy、Δz，即3 个旋转参数：εz、εx、εy，即 1 个尺度因子 k。当公共点数为3个或3个以上时，便可以通过平差的方法求得转换参数。求得转换参数后，再利用上述模型进行各点的坐标转换。

为计算方便，将七参数法转换原理公式展开成多项式形式[7]，多项式模型如下

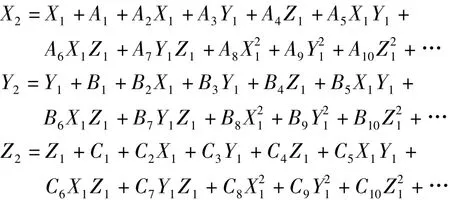
式中，X1、Y1、Z1，X2、Y2、Z2分别为转换前的统一坐标系和转换后的独立坐标系;A1～A10、B1～B10、C1～C10为多项式系数。利用3个或3个以上公共点的两套坐标值，采用最小二乘法解算全部多项式系数再利用七参数法解算转换参数，最后计算待转换点的独立坐标。

三、实例验证

1．试验数据获取

试验地点位于龙岩学院校园内，在测区内设站，并在测量过程中联测到3个以上的已知控制点。那么，这3个以上的控制点就有了独立坐标系和统一坐标系中的两套坐标数据，也可称已知公共点[8]。在坐标转换时，采用七参数法进行坐标转换，利用这些公共点的两套坐标数据计算坐标转换参数，从而将待转的坐标转换为所需的坐标。

试验获取的数据如表1所示，A、B、C、D为已知公共点，1、2、3、4为待转点，具有两套坐标系下的坐标以作检核。

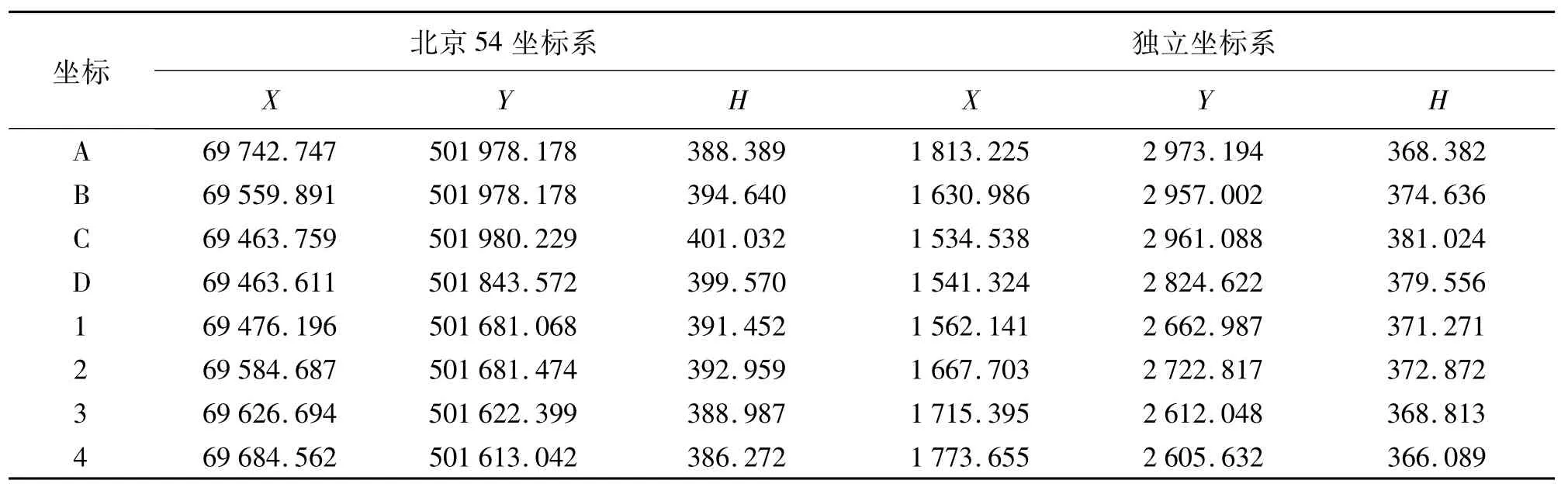
表1 试验数据表

2．坐标转换程序设计

利用C++语言实现七参数坐标转换，流程如图1所示。

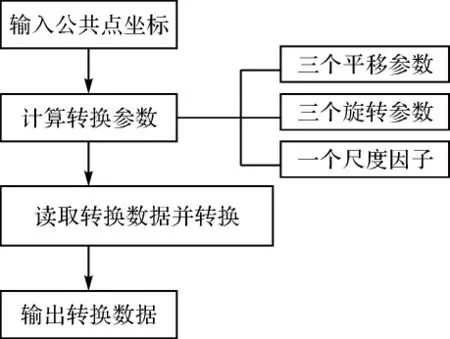
图1 七参数坐标转换流程图

在编辑坐标转换程序的时候，最为重要的是要两坐标系已知公共点的编码。读入3个公共点的坐标，利用七参数法来计算坐标转换参数(3个平移参数，1个尺度因子，3个旋转参数)。需要注意的是，程序设计将以记事本的文件格式进行传输。

坐标转换参数计算完毕后，读入待转换的坐标数据文件，可进行数据转换并输出转换数据。通过转换所得的数据对比原有的数据分析转换是否准确。

坐标转换软件的窗口界面如图2所示。

3．数据转换分析

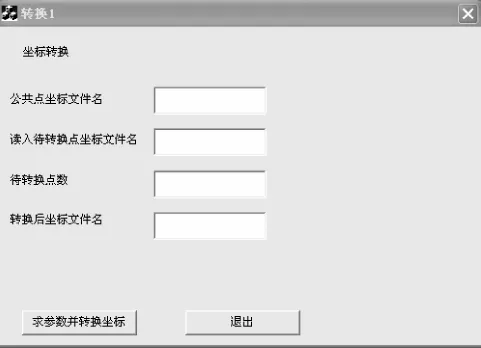
图2 坐标转换软件界面

为检验本软件的准确性，笔者利用CASS软件提供的坐标转换功能，通过对比两者转换后的数据，并分析其转换精度。需要注意的是CASS软件转换坐标是利用直接坐标转换原理，只能转换平面坐标，而不能转换高程。

在CASS软件中转换后的坐标(直接参数法)与在自己编写的坐标转换软件转换后的坐标(七参数法)如表2所示。

表2中*星号点为转换采用的已知点，其余点为转换的检核点。(因为CASS软件坐标转换采用的是直接参数法，没有涉及高程的转换，故而没必要把高程写上去)。

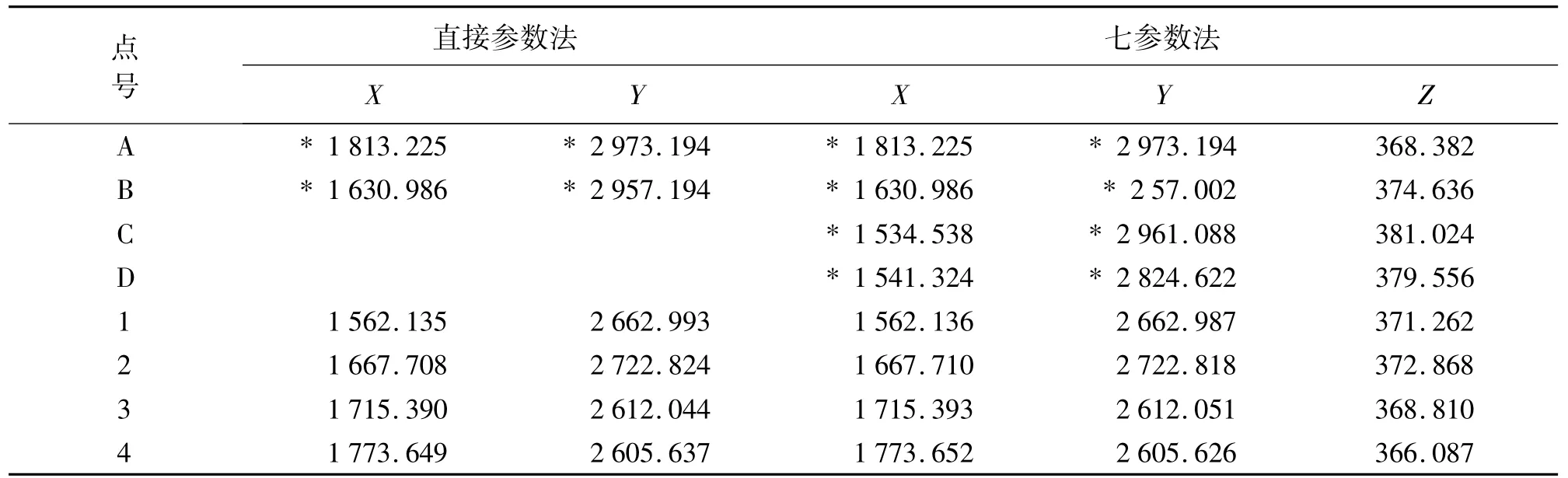
表2 两种方法转换后的数据

CASS软件与本软件转换后的坐标与已知坐标相比较，坐标差对比如表3所示。

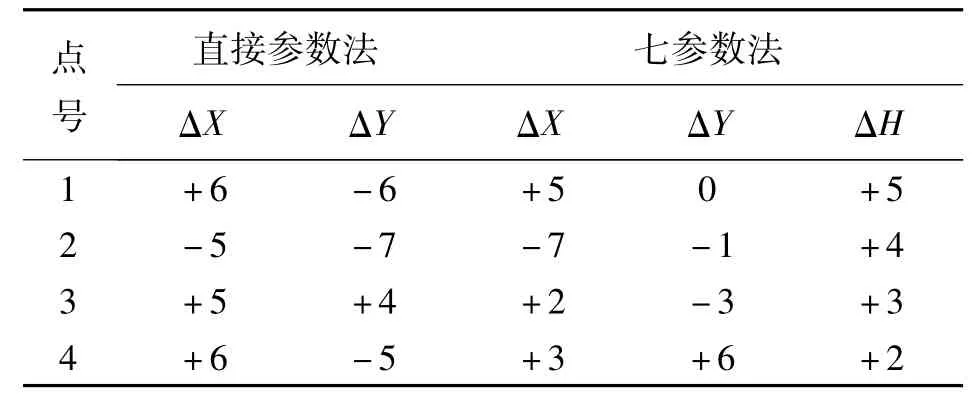
表3 两种方法转换数据与已知数据坐标差 mm

表3中数据表明，采用七参数法进行坐标转换的精度要比采用直接参数法的精度高，而且与直接参数法只能转换平面坐标不同，七参数法转换的是三维坐标。

四、结束语

坐标系转换工作是测量中必要的数据处理工作。本文在探讨了坐标系转换方法的基础上，以七参数坐标转换原理编写三维坐标转换软件，并以实例验证。从试验结果来看，七参数法坐标转换精度，比直接参数法进行坐标坐标转换的精度要高，而且此方法可以转换三维坐标，初步表明了该方法具有较高的实际应用价值。

[1]张述清，李永云．地方独立坐标系统的建立及其实现[J]．测绘工程．2007，16(4)：22-24，29．

[2]彭云英，段文荣，周家明．工程坐标系统的建立及不同坐标系间坐标的相互转换[J]．地矿测绘．2007(2)：22-25．

[3]郭光明，凌金文，匡翠林．工程测量中的坐标变换[J]．岳阳师范学院学报：自然科学版，2002，15(1)：76-78．

[4]朱开文，王占龙．工程独立坐标系的建立及与国家坐标的转换[J]．水运工程．2010(5)：57-60．

[5]蔡昌盛，高井祥，郑南山，等．北京54坐标转换至WGS-84坐标的方法[J]．四川测绘．2005，28(3)：125-127，134．

[6]肖复何．控制测量学[M]．重庆：重庆大学出版社，1994．

[7]牛丽娟．测量坐标转换模型研究与转换系统实现[D]．西安：长安大学，2010．

[8]王林．假设坐标系到统一坐标系的简易转换原理及VB程序设计[C]∥华东地区第十次测绘学术交流大会论文集．江苏：[s．n．]，2007．