不同空间分辨率图像匹配

关泽群，刘晓青

(同济大学测绘与地理信息学院，上海200092)

一、引 言

图像匹配是多种图像处理和应用的基础，匹配的效果对于后续的图像处理具有关键性的影响。遥感图像的多源化使得信息量丰富的同时，其图像数据间的差异也对图像匹配提出了挑战。目前对于同一传感器、不同时相的遥感图像匹配技术已经比较成熟，而对于不同尺度、多源遥感图像之间的配准，则是目前研究的热点和难点，长期以来一直未能很好地解决[1]。

Yves Dufournaud等研究了不同空间分辨率图像的匹配问题，建立了高分辨率图像的多尺度表达，在尺度空间中提取角点，将传统的一对一配对变为一对多的匹配[2]。Lowe在1999年首先提出了SIFT(scale invariant feature transform)，即尺度不变特征变换算法，引起了国内外摄影测量与遥感界的广泛关注，并在2004年对其进行了完善[3]。Yves Dufournaud和Lowe等利用尺度空间思想模拟出分辨率相近的图像进行匹配，本文将超分辨重建技术引入图像匹配中，拟通过超分辨率重建技术提高低分辨率图像分辨率，从而缩小图像间分辨率差异，提高图像配准精度。

国内外学者在超分辨率算法研究方面做了许多工作，致力于改善图像超分辨率重建的效果，获得更高分辨率的图像，然而将超分辨率技术应用到不同空间分辨率图像匹配上的却很少。唐斌兵等提出了一种利用先验图像的灰度分布作为约束的图像超分辨率重建的新方法，利用最小鉴别信息构造重建图像与先验图像的约束，约束结果使得重建图像与给定的先验图像具有最相似的灰度分布[4]。黄全亮等在基于特征图像的配准过程中引入了超分辨技术，经过仿真试验比较，结果表明超分辨率后特征点的定位更准确[5]。本文采用文献[4]的方法对利用高分辨率图像作为先验信息对图像进行超分辨率重建，图像特征提取及匹配基于文献[2]及[6]。

二、超分辨率重建算法

1．图像退化的数学模型

图像的采集、传输和记录等过程中，光学系统的像差、大气的扰动、运动模糊、离散采样以及系统噪声等不良因素都会造成图像细节模糊、分辨率下降。用矩阵-向量的方式来描述图像的退化过程，低分辨率图像的数学模型可表示为

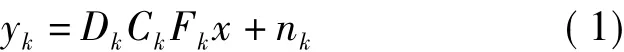
式中，x表示高分辨率图像;yk表示第k帧低分辨图像;nk表示零均值加性高斯噪声;Dk、Ck和Fk分别表示下采样矩阵，模糊矩阵和几何变换矩阵。令Hk=DkCkFk，则有

式中，Hk称为退化矩阵。上式是常用的图像重建模型。

超分辨率重建就是利用已有的观测数据和其他相关信息，通过建立的数学模型获取在一定准则下高分辨率图像x的较好估计，它是成像退化过程的逆过程。

2．正则化超分辨率复原

由于图像超分辨率重建问题是对一个病态问题求逆的过程，则在确定一个低分辨率图像序列的条件下，必定存在一个图像集合是满足给定条件。对这一问题的解决的可行方法是依据先验知识，对解空间进行约束，并使方程收敛于某个最优解。

正则化方法主要是通过加入恰当的约束信息，即引入有关高分辨率图像的先验信息约束，一方面改进逆问题的不适定性，另一方面引入新的信息，改善图像的分辨率。为获得高分辨率图像，就必须合理利用相关的先验信息。一般来说，超分辨处理所能达到的效果，与所观测数据的完全性和先验信息等因素有关。先验信息的开发与合理利用，是利用正则化方法提高图像分辨率的关键问题之一。正则化方法构造附加约束把不适定问题转化为适定问题，通常需要求解如下表达形式的目标泛函的极小值[5]

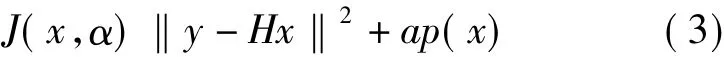
式中，d(x)=‖y-Hx‖2为数据拟合项，保证原问题“相邻近”问题的解在真解的邻域内连续地依赖于观测数据;p(x)为正则项，保证问题解的稳定性;α为正则化参数，起权衡数据项和正则项的作用。正则化项对未知图像x形成了一个约束，它根据图像的先验信息对解进行约束，通常是基于一阶微分或二阶微分的高通滤波器算子。这种思想体现出超分辨率重建问题的本质就是在充分拟合观测数据的前提下，使某种奇异性度量最小，从而寻找理想的解x。因而，如何选取约束算子是区分不同正则化方法的标志。正则化项的构造，关键在于确定解的先验信息的具体形式。正则化参数起着对解的折中作用，α越大，其重构图像灰度越接近先验图像灰度。因此，在α选取上，原则上认为先验图像越接近于原始高分辨率图像，α取值越大。但是，由于实际应用中高分辨率图像f往往是不可获得的，需要采取合理的方法计算α值。

约束算子的选择是基于正则化超分辨率图像重建算法的关键。人眼视觉认为空间灰度分布相似的两幅图像具有相同的清晰度，因此利用与原始图像空间灰度分布相似的清晰图像作为一种清晰特征，可以对图像的盲重建结果进行约束[4]。

对于随机变量X，概率密度函数q(x)未知，先验概率密度函数为p(x)，对函数q(x)的估计应满足以下两个条件

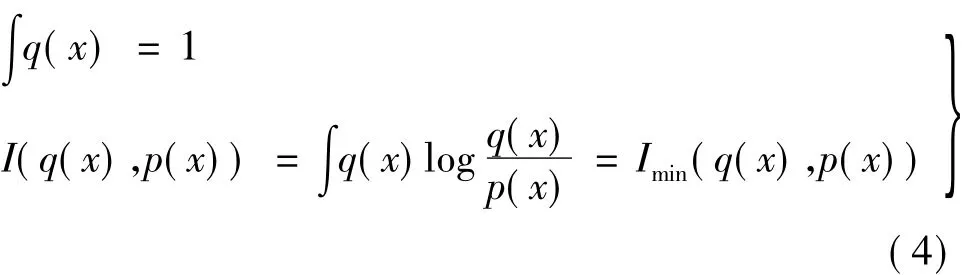
记k为先验特征图像;f为待求的超分辨率图像，则有

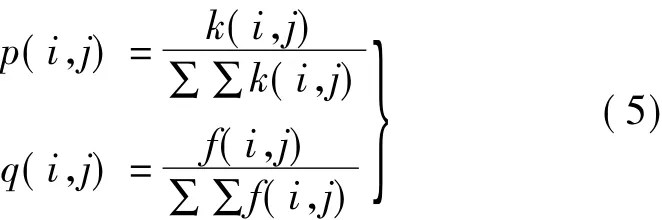
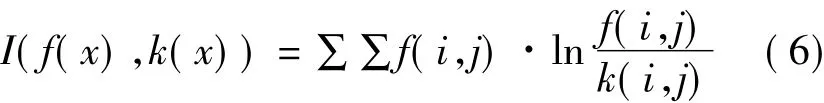
以此作为正则化的约束项，即令 p(x)=I(f(x)，k(x))，代入式(3)中进行迭代求解。本文中以高分辨率图像作为先验特征图像k，具体的求解方法可参考文献[4]。

三、Canny边缘检测与边缘特征点匹配

在不同空间分辨率下的图像匹配，由于图像间存在的尺度差异及辐射差异等，传统的图像匹配算法可能难以得到匹配结果。考虑到边缘对于辐射差异及尺度差异具有一定的鲁棒性，可以引入边缘检测算法对不同空间分辨率图像进行匹配。Canny算子是应用较为广泛的边缘检测算子之一，具有较好的边缘检测效果。具体算法包括4个步骤：高斯滤波平滑、梯度计算、非极大值抑制、双阈值检测[7]。

在提取边缘线后，为了提高后续的特征匹配效率和正确率，须去除较破碎的边缘线。本文通过计算边缘线的长度，设定边缘线长度阈值，删除小于阈值的边缘线。

Canny算子提取到待匹配图像的边缘点后，采用特征点匹配的方式找出点间的对应关系，本文采用成本函数法匹配边缘点[6]，如图1 所示[1]。

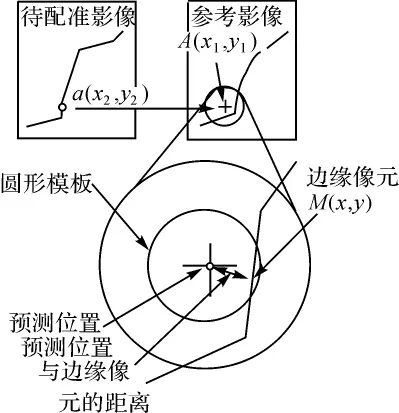
图1 Canny边缘点匹配

首先将待匹配图像边缘点坐标a(x2，y2)代入仿射变形公式，计算其在参考图像上的预测位置A(x1，y1)，仿射变形公式中的参数由SIFT匹配结果计算得出。然后以预测位置为圆心，取半径为5像素的圆形模板，将参考图像中位于模板内的边缘点M(x，y)代入成本函数式(7)中[6]

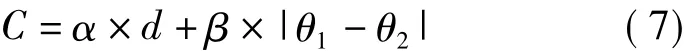
式中，α、β分别为距离权重和方向权重;α取值为边缘点M与预测位置最大距离的倒数;β取值为边缘点M与预测位置最大方向差的倒数;d为边缘点M与预测位置的距离，θ1、θ2分别为待匹配图像边缘点a与参考图像边缘点M的梯度方向。

计算出各边缘点的C值，C最大的点为可能的匹配点Mp。按照上述步骤计算Mp点在待匹配图像上的C值，若C值最大的点为a，则判定为匹配点。具体方法可以查阅文献[6]。

最后对匹配点对进行去误匹配操作，得到最终的匹配结果，本文采用最小二乘法计算x，y方向偏差值，去除偏差大于1的点。

四、试验及结果分析

1．试验设计

试验图像数据为Landsat ETM+同一区域第8波段图像与第6波段图像，标示分辨率分别为15m、60m，图像大小分别为 400 dpi×400 dpi、100 dpi×100 dpi，如图2所示，试验采用的平台为Matlab。

图2 试验原始图片

试验流程图如图3所示。

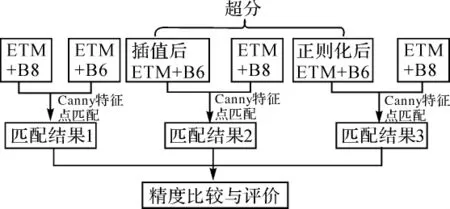
图3 试验流程图

2．超分辨率重建

首先，对Band 6图像进行超分辨率插值，采用的方法为双三次卷积法，得到大小为400 dpi×400 dpi的图像。

接着，采用文献[4]提出的最小鉴别信息约束方法对插值后图像进行超分辨率复原。本试验中降质点扩散函数为高斯函数，窗口大小为8 dpi×8 dpi，σ =2，正则化参数 α =0．9，超分辨率重建结果如图4所示。

图4 正则化超分辨率重建后ETM+6

3．图像匹配

本文采用SIFT算法计算Canny边缘特征点匹配算法需要的初始匹配参数，若图像间差异过大，则需要人工选取至少3对同名点进行粗匹配来获得初始匹配参数;采用仿射模型作为两幅图像的几何变换模型

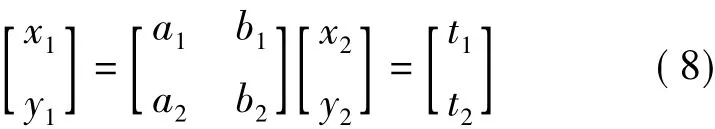
由匹配点对按照仿射变换模型计算几何变换参数，由于缺乏理论值作参照，本文采用均方根误差(RMSE)衡量匹配的总体精度

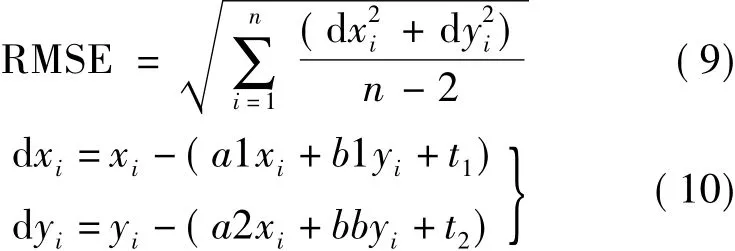
1)ETM+Band8和ETM+Band6的匹配结果如图5所示，得到匹配点对29对，根据匹配点对求得的几何变换参数及RMSE如表1。

图5 ETM+Band8与ETM+Band6匹配结果

2)ETM+Band8和插值后ETM+Band6的匹配结果如图6所示，得到匹配点对340对，根据匹配点对求得的几何变换参数及RMSE如表2。

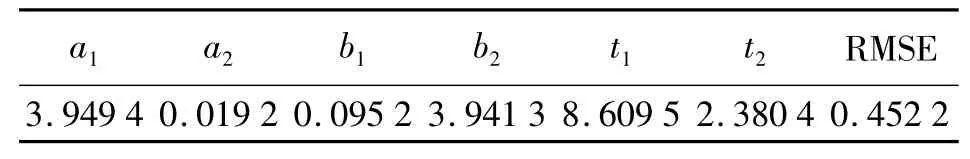
表1 几何变换参数及RM SE

图6 ETM+Band8与插值后ETM+Band6匹配结果

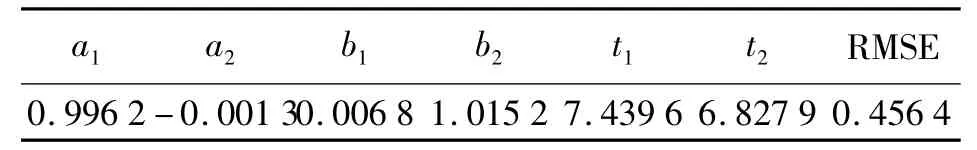
表2 几何变换参数及RMS E

3)ETM+Band8和基于正则化超分辨率重建后ETM+Band6的匹配结果如图7所示，得到匹配点对422对，根据匹配点对求得的几何变换参数及RMSE如表3。

图7 ETM+Band8与正则化超分后ETM+Band6匹配结果

表3 几何变换参数及RMSE

4．结果分析

如匹配结果图所示，正则化超分辨率重建后图像匹配点对相对于原始图像数目增加，同时分布区域更加均匀，RMSE减小，说明正则化超分辨率重建后的配准误差减小。超分辨率重建恢复了图像遗失的部分信息，使得图像细节信息更加丰富，能够提取更多的特征;正则化修正图像插值后的错误信息，使得提取的特征较为正确。本文提取图像的Canny边缘点进行图像匹配，有利于充分发挥图像超分辨率重建的作用，结果显示经过正则化超分辨率重建后图像匹配效果及配准精度得到改善。

Canny边缘特征点匹配能够得到较多的匹配点，但也存在误匹配现象，通过最小二乘法去除偏差较大的点最终可以获得较小的配准误差。对于具有明显边缘的图像来说能够取得较多的匹配点，具有很好的配准效果。

五、结束语

多源遥感图像匹配是近年来研究的热点和难点。通过超分辨率重建技术可以提高图像的空间分辨率，从而缩小图像间的分辨率差异。本文利用高分辨率图像灰度分布信息对低分辨率图像进行超分辨率重建，该方法较适用于灰度分布相差不大的图像间匹配。超分辨率重建结果与重建过程中选取的参数值关系密切，且图像质量提高的程度有限，超分辨率算法的选择及其在图像匹配中的应用有待进一步探索。高低分辨率图像间的相似性为低分辨率图像的超分辨率重建提供了相应的先验信息，如何选取合适的超分辨率重建算法，进一步提高图像的品质，同时使其能够更好地应用于图像匹配，这是今后值得研究的问题。

[1]王万同，韩志刚，刘鹏飞．基于SIFT点特征和Canny边缘特征匹配的多源遥感影像配准研究[J]．计算机科学，2011，38(7)：287-289．

[2]DUFOUMAUD Y ，SCHMID C，HORAUD R．Matching Imageswith Scale Adjustment[J]．Computer Vision and Image Understanding，2004，93：175-194．

[3]LOWE D G．Distinctive image features from scale-invariant key points[J]．International Journal of Computer Vision，2004，60(2)：91-110．

[4]唐斌兵，王正明．基于先验约束的图像超分辨率重建[J]．红外与毫米波学报，2008，27(5)：289-392．

[5]黄全亮，孙坤，刘水清．超分辨率技术对基于特征图像配准算法的影响[EB/OL]．[2011-01-26]．http：∥www．paper．edu．cn．

[6]HONG T D，SCHOWENGERDT R A，A Robust Technique for Precise Registration of Radar and Optical Satellite Image[J]．Photogrammetric Engineering ＆ Remote Sensing，2005，71(5)：585-593．

[7]靳艳红，蒙建军．一种基于Canny算子改进的边缘检测算法[J]．2011，30(2)：27-30．