Landsat-5遥感影像精度分析

杨 中，李国庆，解吉波，颜韵旋

(1．中国科学院对地观测与数字地球科学中心数字地球重点实验室，北京100094;2．中国科学院研究生院，北京100049)

一、引 言

随着遥感技术和计算机技术的迅速发展，遥感技术应用的范畴已经从当初的单一遥感技术发展到包括遥感(RS)、全球定位系统(GPS)、地理信息系统(GIS)等技术在内的空间信息技术。遥感影像已成为人类获取空间信息的重要数据源。现代遥感技术随着应用的深入，遥感影像的质量评价问题受到了广泛的关注。遥感影像的几何质量表达了影像能正确恢复(量测)原始景物形状的能力[1]。数字影像的几何质量主要是通过影像在摄影测量定位方面的能力来表达，其中遥感影像真实分辨率是判断其几何质量优劣的重要指标之一。本文介绍了两种评定遥感影像平面精度的方法，并比较了这两种方法对平面精度评定结果的影响。通过比较不同的评定方法，最终采用点位中误差方法和重心坐标求和方法分别对Landsat-5的平面精度和真实分辨率进行评定。

二、试验数据

1．Landsat-5简介

Landsat即“地球资源卫星”计划，在美国内务部和国家宇航局的共同努力下，于1972年7月23日发射了第一颗地球资源卫星(1975年后改名为“陆地卫星”)。陆地卫星已经发射了6颗，目前Landsat-5和Landsat-7仍在运转工作[2]。Landsat-5卫星是目前在轨运行时间最长的光学遥感卫星，该卫星获得的遥感影像是迄今为止在全球应用最为广泛的地球资源卫星遥感信息源之一[3]。Landsat-5卫星的TM传感器数据是目前中国科学院对地观测与数字地球科学中心为用户提供的主要遥感卫星数据源之一。Landsat-5的轨道为近极地近环形太阳同步轨道，轨道高度为705 km，倾角为98．22°，扫描带宽度为 185 km，重复周期为 16 d[4]。

2．研究区域和试验点

本文选取内蒙古呼伦贝尔市西北部为研究样区，该区域地形特点明显。样区地势由东向西逐渐降低，最低点海拔约363 m，最高点海拔约1407 m，东半部为山地，西半部为平地。试验点应均匀分布于研究样区，且尽可能到达研究区域的边缘，同时试验点的位置必须在遥感影像上清晰可辨。为便于描述，将遥感影像上提取的点称为“检测点”，将其对应的测量点称为“同名点”。平面精度和真实分辨率精度是通过计算检测点和同名点获得。以GPS采取的测量点为试验点，在研究样区进行了差分GPS测量，获得34处地面实测地理坐标作为试验点。

三、精度评定方法

1．平面精度评定方法

遥感影像的平面精度也称几何定位精度，或像素精度，即遥感影像上各像素点经坐标配准以后的相对位置是否准确，是否残余明显的畸变差[5]。评定误差最常用的方法是中误差法，以下介绍两种评定平面精度的方法，并对这两种方法进行比较。

(1)间距中误差法

计算各检测点连线与其对应的同名点连线长度差值的中误差，即可得遥感影像的平面精度S。

设有m个检测点，则共可组成n条边

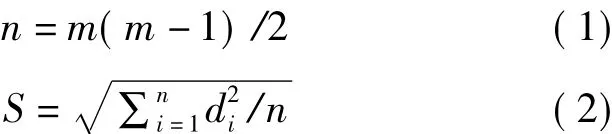
式中，Δdi=di-di'(i=1，2，3，…，n);di为检测点连线的第i条边的长度;di'为对应同名点连线的长度;S为求得的连线长度差值的中误差，即遥感影像的平面精度。

(2)点位中误差方法

检测点和同名点之间，由于存在坐标分量误差Δx，Δy而产生平面误差因此，可以根据坐标分量分别统计误差。点位中误差法即分别计算每个检测点与同名点X方向，Y方向及该点处的平面误差，然后分别求得X方向，Y方向的中误差以及各点平面误差的中误差。

设第i个检测点的X方向坐标值为dxi，Y方向坐标值为dyi;对应同名点的X方向坐标值为d'xi，Y方向坐标值为d'yi，则X方向误差为方向误差为，该点平面误差为那么，X方向中误差为

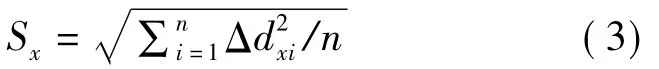
Y方向中误差为

平面中误差为

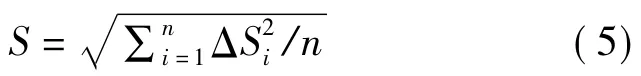
式中，n为误差个数。X方向中误差Sx为遥感影像在X方向的平面精度，Y方向中误差Sy为遥感影像在Y方向的平面精度，平面误差S为遥感影像的平面精度。

(3)两种方法比较

为便于讨论，假设检测点A、B、C位于一条直线上，对应同名点 A'、B'、C'也位于一条直线上，即只考虑X方向的误差，忽略Y方向的误差(见图1)。设点 A、B、C 的 X 方向的坐标值分别为 ax、ay、az由于3个点位于一条直线上，故Y方向的坐标值相同，设为y;点A'、B'、C'的X方向的坐标值分别为ax'、by'、cx'，Y 方向的坐标值设为 y'。

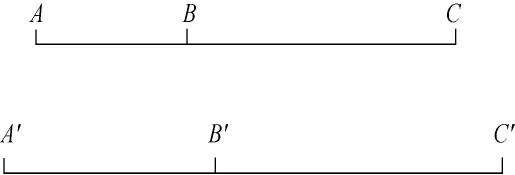
图1 点A、B、C的位置

令

记点A至点B的距离为PAB，点B至点C的距离为PBC，点A至点C的距离为PAC，则

同理，点A'至点B'的距离为

点B'至点C'的距离为

点A'至点C'的距离为

那么，根据间距中误差法公式(2)计算的平面精度为

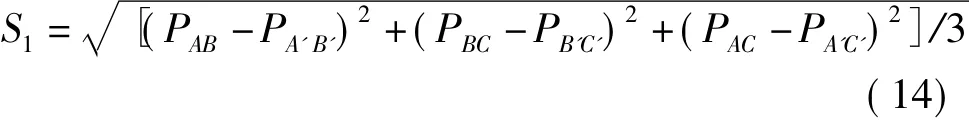
为便于计算，可将上式改为

下面根据点位中误差公式(5)计算平面误差。第1个检测点的平面误差(即点A与点A'的平面误差)为

第2个检测点的平面误差(即点B与点B'的平面误差)为

第3个检测点的平面误差(即点C与点C'的平面误差)为

那么，根据点位中误差公式(5)计算的平面精度

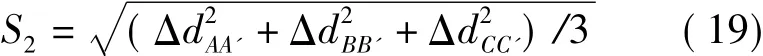
为便于计算，可将上式改为

假设C的位置不准确，将其X方向误差放大Δx，即cx变为cx+Δx，计算此次平面精度。此次间距中误差法求得的平面精度记为S11，那么平面误差增大的值为

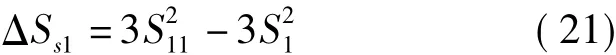
同理，此次点位中误差法求得的平面精度记为S22，那么平面误差增大的值为

将式(6)～式(13)、式(15)代入式(21)得

将式(6)～式(7)、式(16)～式(18)代入式(22)得

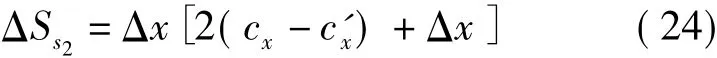
比较式(23)和式(24)可以看出，当将 C的X方向误差放大Δx，间距中误差法求得的平面精度比点位中误差求得的平面精度误差大Δx2，所以点位中误差方法求得的平面精度更准确。

目前，采用的遥感影像平面精度评定模型多为中误差模型，误差结果只给出整体的平面精度结果，并没有给出X方向和Y方向的平面精度误差，因此不能揭示误差中的系统成分。点位中误差法求得的中误差能直观反映在各方向上误差的大致数值，其中X方向误差、Y方向误差能揭示误差的系统成分，平面误差能反映误差的整体离散程度，因此，本文介绍的点位误差不失为评定遥感影像平面精度的好方法。本文第4节对Landsat-5进行平面精度评定的方法即为点位中误差法，为了更好地揭示误差中的系统成分，将统计X方向最大绝对误差、Y最大绝对误差和最大平面误差。

2．真实分辨率评定方法

真实分辨率评定采用了重心坐标求和方法[4]。首先分别计算n个检测点和n个同名测量点的重心坐标O和O'，然后计算检测点和同名点到各自重心坐标的距离h、v和 x、y，求和并取商。

式中，S为n个检测点到重心坐标O的像素总和，单位为像素。S'为n个同名点到重心坐标O'的距离之和，单位为m。

真实分辨率RES为

四、精度评定结果

按照上述精度评定的方法，试验的主要步骤如下：

1)获取遥感影像研究样区。将Landsat-5进行投影转换、校正、彩色合成后，用研究样区矢量数据裁剪影像，最终得到Landsat-5样区范围。

2)选取检测点。试验点的地理坐标投影转换为与Landsat-5相同的平面投影。将实际测量的点记为“同名点”，在影像上选取对应的同名点为“检测点”。在每一检测点的像素上作标记并编号，记录每一检测点的像素位置和坐标值。

3)平面精度计算。根据点位中误差法计算Landsat-5的平面精度。图2～图4为计算的各个试验点的误差，其中图2为各个试验点在X方向的误差分布图，图3为各个试验点在Y方向的误差分布图，图4为各个试验点平面精度的误差分布图。表1为Landsat-5平面精度评定结果。

图2 X方向误差

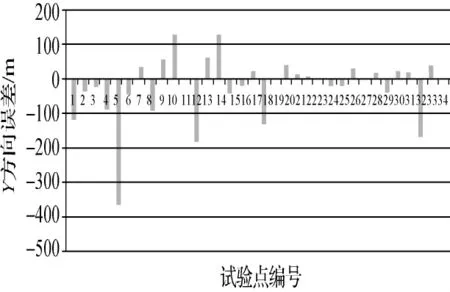
图3 Y方向误差

图4 每个试验点处的平面误差

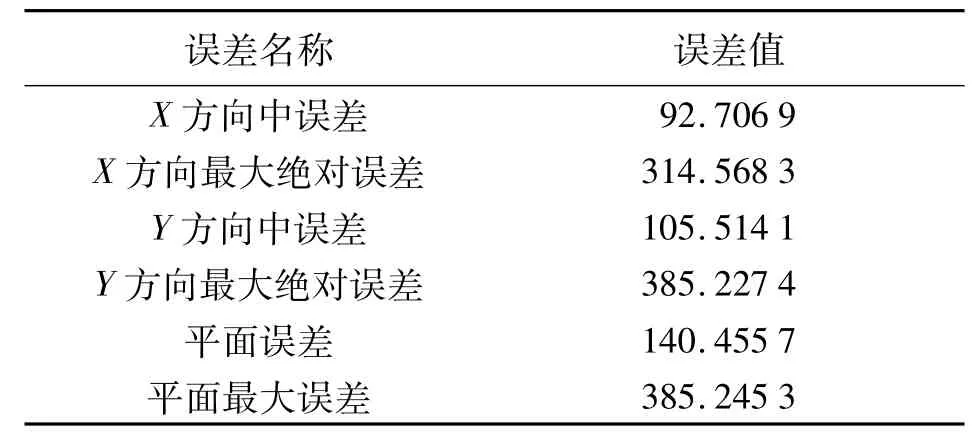
表1 Landsat-5平面精度评定结果 m

4)真实分辨率计算。根据重心坐标法计算Landsat-5的真实分辨率。计算检测点到重心坐标的像素之和为137 622像素，同名点到重心坐标的距离之和为3 287 052．878 7m。由此可得Landsat-5的真实分辨率为23．884 6m/像素。

五、结束语

Landsat-5的平面误差为140．455 7m，平面最大误差为385．245 3m。从误差分量分析，Landsat-5 X方向中误差为 ±92．706 9 m，X方向最大误差为314．568 3m，Y 方向中误差为 ±105．514 1m，Y 方向最大误差为385．227 4m，可以看出，X方向中误差，最大绝对误差均小于Y方向，因此，Landsat-5 X方向的几何定位要优于Y方向。

Landsat-5的真实分辨率为23．884 6m/像素，其标称分辨率是30m，所以Landsat-5标称分辨率的准确度大约为 1-|30-23．884 6|/30=79．62%。

[1]王昱，胡莘，张保明．数字影像质量评价方法研究[J]．测绘通报，2002(5)：7-9．

[2]梅安新，彭望绿，秦其明，等．遥感导论[M]．北京：高等教育出版社，2001：50-51．

[3]陈俊，网文，李子扬，等．Landset-5 TM 数据的辐射校正与几何定位精度[J]．中国图像图形学报，2008，13(6)：1094-1100．

[4]中国科学院对地观测与数字地球科学中心．陆地卫星5 号[EB/OL]．[2009-10-01]．http：∥ids．ceode．ac．cn/satellite．aspx?satlsid=7．

[5]陈泽民，马荣华．IKONOS卫星遥感影像的精度分析[J]．遥感技术与应用，2002，17(1)：46-52．